分工况下风电机组各变量相关性研究

崔双双，孙单勋

（暨南大学 能源与电力研究中心，广东 珠海 519070）

0 引言

风能作为我国重要的清洁能源之一，资源丰富且开发利用价值巨大，是实现碳达峰、碳中和目标的重要能源。随着支持政策的出台和风力发电技术的成熟，近几年风力发电飞速发展［1］。

风力资源通常受地理因素影响较大，其主要集中在我国的“三北”地区，存在远距离输电的状况。现有的并网模式下，风电机组一旦出现故障便会造成极大的影响，甚至会导致机组脱网的严重后果［2-3］。一方面，风电功率受众多因素影响，如风速、风向、温度、气压、扭缆角度、机舱角度等，这些因素相互关联和影响，使风电功率预测和控制变得十分复杂［4］；另一方面，风电机组装机容量大规模增加，风力发电本身具有间歇性、随机性和波动性，给电网的经济调度带来了困难［5-6］，机组输出功率的平稳性、可控性较差，给电网安全运行带来挑战［7-9］。因此，分析与掌握风电机组间变量的相关特性、对风电机组可能出现的故障进行预测、对可能出现的较大风电功率进行捕捉，可以更好地利用风能资源，有助于解决我国环境污染和能源短缺问题。

近年来，国内外对风电场变量相关性的研究不断深入：孙若迪等［10］根据风速-负荷联合二元正态分布函数，用Monte Carlo 法对风速-负荷序列进行抽样，反映时序风速和负荷的相关性，提高可靠性计算的精确性。谢远强［11］通过Pearson 相关系数对风电机组状态参数进行相关性分析，为风电机组异常状态辨识和缺陷预警提供依据。季峰等［12］利用混合Copula 函数建模分析风电功率相关性的方法，分析了风电功率间的尾部特征，刻画出风电功率间的相关结构和尾部特征，同时求取反映相关程度的指标。罗兴艳等［13］在配电网中应用非参数核密度概率估计和Copula 理论，得出风速和负荷在一定程度上具有相关性的结论。丁家满等［14］提出了基于Copula 函数的电网规划指标相关性分析及建模方法，证明了Copula 函数在刻画相关性方面的有效性。苏晨博等［15］利用贝叶斯线性回归算法建立混合Copula 函数模型，计算风电场之间的出力相关性，提高了拟合得到的相关性和出力概率分布的准确性。上述文献的相关研究大多局限于同一工况下的2 个变量且变量间高度符合高斯分布的情况，还缺少针对性的、对多变量以及多变量间不符合高斯分布的情况和分工况下相关变量的研究。

本文在对广东某海上风电场风电机组数据采集与监视控制（SCADA）系统的长期监测数据进行分析研究的基础上，提出Copula 熵在风电机组相关变量研究方面的应用。对该海上风电场风电机组变量之间的Copula 熵进行计算并与变量的Pearson相关系数和Spearman 系数进行对比，发现Copula 熵在风电场的变量相关性描述方面具有优越性。最后，针对不同工况下风电机组运行特性差异较大的情况，采用聚类分析对不同工况进行划分，计算不同工况下各变量的Copula 熵，研究划分工况下各变量的相关性。

1 相关性分析理论

1.1 Pearson相关系数

Pearson 相关系数［16］由英国统计学家皮尔逊于20 世纪提出，可用于计算数据连续且满足正太分布的变量间的线性相关。2 个变量间的Pearson 相关系数定义为2个变量间协方差和标准差的比值，

式中：X，Y为随机变量；N为变量取值个数。

1.2 Spearman相关系数

Spearman 相关系数［17］在统计学中广泛应用，主要用于估计2 个变量之间的依赖性，其大小与变量数值无关，只与其中元素排序位置有关。针对2 个元素个数为N的随机变量或集合X，Y，对集合中的元素进行统一的升序或降序排列，得到新的排列后的序列X，Y。xi和yi分别为集合X和Y中排序为i的元素，则随机变量X，Y之间的Spearman 相关系数可由xi和yi计算得到，即

1.3 Copula熵理论

Copula 函数理论由Sklar 于1959 年提出，是一种统一表示随机变量之间统计关联关系的理论工具［18］。该函数可将1 个联合分布分解为n个边缘分布和1 个Copula 函数，这个Copula 函数描述了变量间的相关性。Copula 函数最初在金融领域应用，现在已广泛应用于其他工程技术领域，如电力系统领域的风电、光伏等间歇性能源建模问题。

Copula函数的表达为

式中：X1，X2，…，XN为N个随机变量，其各自的边缘分布分别为F1(x1)，F2(x2)，…，FN(xN)；联合分布函数为H(x1，x2，…，xN)，根据边缘分布累积分布函数（CDF）逆 变 换 有xi=F-1i(ui)(i= 1，2，…，N)，ui=Fi(xi)(i= 1，2，…，N)。

根据Copula 函数概念，清华大学教授孙增圻［19］提出了Copula 熵（Copula Entropy，CE）理论，其本质上是一种Shannon 信息熵［20］理论。互信息（MI）为信息论中的一种信息度量，可以看成是一个随机变量中包含关于另一个随机变量的信息量［21］，是一种理想的统计独立性度量概念，可以用来解决多个统计学基本问题。Copula熵在对变量间的相关程度进行描述的同时，还能反应变量间相关性的结构信息，其熵值越小，说明所包含的信息量越多，目前主要应用于结构学习、关联发现、变量选择、时序因果发现等方面。

Copula熵定义为

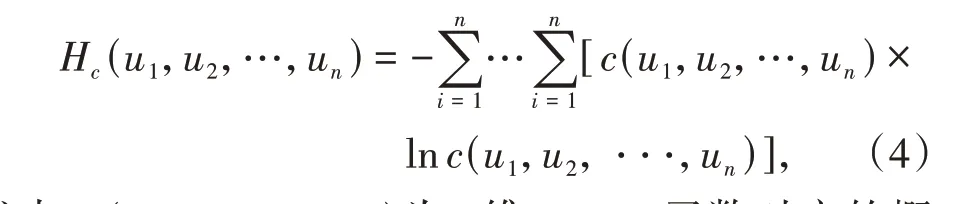
式中：c(u1，u2，···，un)为n维Copula 函数对应的概率密度函数；ui(i= 1，2，···，n)为随机变量的边缘累积分布函数。

2 全工况下各状态变量相关性分析

本文选取了广东省某海上风电场具有代表性的风电机组进行相关性分析，研究其各变量间的耦合关系。对2021 年1 月的风电机组相关状态信息进行分析，研究风电机组状态信息与风电机组有功功率的相关性。

2.1 相关变量选取

考虑到风电机组运行过程中容易受到外部环境突变、塔架振动、风电机组变桨等因素带来的干扰，因此对SCADA数据中的原始状态参数风速做差分处理，计算前一时刻状态变量和后一时刻状态变量的差值，构造出衍生特征变量——风速差分，其差值较大则表明风电机组状态发生突变，可利用这个变量分析风速和风电机组有功功率间的相关性。

风电机组传感器带来大量状态变量信息的同时也包含了大量的噪声和不相关数据。为了提高本文数据分析的准确性，在众多SCADA数据中选取具有代表性的状态信息并结合风速差分进行一系列相关性分析［22］。图1—3 中的样本容量表现为风电机组的时序状态信息，具体表现为1 月风电机启动数量随时间从0开始逐渐增加到545。

2.1.1 风速、风速差分与风电机组有功功率相关性分析

图1a 为风速、风电机组有功功率和样本容量在1月的变化；图1b描述了风电机组风速差分、风电机组有功功率和样本容量随时间的变化趋势。

分析图1a 中风速和风电机组有功功率的变化特点，可以看出整体上风速呈先增大后减小的锯齿状，数值变化幅度较大且随时间变化呈一定的周期性。风电机组风速随时间变化的曲线和风电机组有功功率随时间变化的曲线基本上重合，因此两者呈正相关。图1b 中风电机组风速差分呈整体离散且均匀地分布在某一数值范围内，不具有上升或下降趋势，与有功功率变化趋势完全不同，两者不相关。

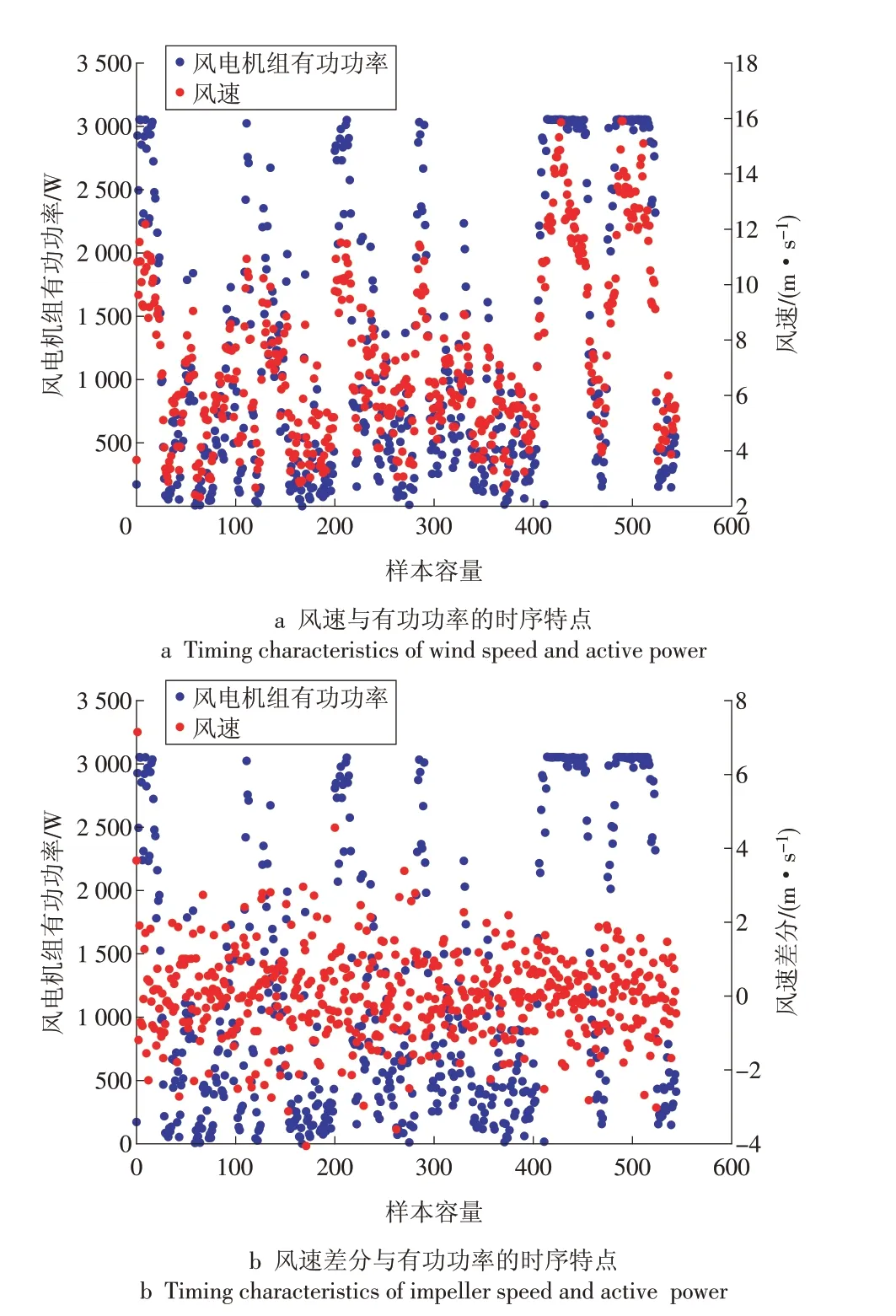
图1 风速、风速差分与有功功率的时序趋势Fig.1 Temporal trends of wind speed， wind speed difference and active power

2.1.2 各类部件温度-风电机组有功功率相关性分析

图2分别描述了风电机组轴箱温度和其对应的发电机绕组温度与风电机组风电机组有功功率和样本容量的变化趋势。

对图2a 中散点变化进行规律分析，轴箱温度数值整体变化幅度不大且点集集中。在风电机组有功功率数值较大区域，轴箱温度数值增大或减小的幅度与风电机组有功功率变化幅度基本重合，两者存在一定正相关关系。图2b中，当风电机组有功功率大于300 W 时，发电机绕组温度和风电机组有功功率在整个样本范围（0 —545）内变化趋势基本相同，数值变化范围完全重合，因此两者具有较强的正相关关系。

图2 轴箱温度、发电机绕组温度与有功功率时序趋势Fig.2 Axle box temperature， generator winding temperature and active power timing trend

2.1.3 关键部件扭缆角度-风电机组有功功率相关性分析

图3 的2 张散点图分别描述了风电机组桨叶角度和其对应的扭缆角度与风电机组有功功率和样本容量的变化。

根据图3 分析发现，风电机组桨叶角度和扭缆角度与风电机组有功功率基本不存在相关性。图3a 中桨叶角度数值整体变化范围不大，走势较平稳，与风电机组有功功率数值急剧变化的锯齿状图形成鲜明对比。其中，1 月后期桨叶角度变化幅度较大，呈山谷状，其变化趋势与风电机组有功功率的变化趋势基本不相同。图3b 中，1 月中期风电机组扭缆角度数值较大，可达到400°，其余时间段风电机组扭缆角度离散分布在0°以下。两者变化曲线和风电机组有功功率变化曲线不相同，因此两者和风电机组有功功率基本不具有相关性。

2.2 相关状态变量数理性分析

风电机组在不同的工况下，功率也有所不同。因此，综合考虑风电机组各种状态参数对风电机组有功功率的影响，本文对特征状态变量及风速差分与风电机组有功功率进行了基于Pearson相关系数、Spearman 相关系数和Copula 熵的数理性分析，其中Copula 估计熵计算采用Python 的Copent 包［23］，采用3种相关系数的分析结果见表1。

由表1可以看出，3种方法计算所得数值大体上保持一致，Copula 熵在描述变量参数一致性方面与Pearson系数和Spearman系数具有一致性，且比他们具有更广泛的数值变化范围。根据Pearson 相关性分析原理，相关系数绝对值越接近1 时，相关性越强，相关系数绝对值越接近于0 时，其相关性越弱，表现为二阶依赖关系［-1，1］间的相对强度［23］。用Spearman 相关系数来衡量2 个变量的依赖性，当2个变量完全单调相关时，其数值为+1 或-1。Copula熵表现为所有阶依赖关系的正关联强度，其数值越大，相关性越强。分析表1 中的数据可知，风速、发电机绕组温度与风电机组有功功率均具有较强的相关性，相关性越强，数值越大，轴箱温度与风电机组有功功率中度相关；扭缆角度、桨叶角度和风速差分与风电机组有功功率相关性极弱或不相关。

表1 不同状态变量与有功功率相关系数Table 1 Correlation coefficients between different state variables and active power

其中轴箱温度的Copula 熵和其他2个相关系数的差异较大。据图1—3可知，只有轴箱温度的数值变化符合高斯分布。高斯分布情况下，有

式中：ρx为相关系数矩阵；Hc(x)为Copula熵。

分析表1 中的数据发现，Copula 熵在描述变量相关性时数值变化范围更广，对变量相关性的强弱程度表现得更具体。在Pearson系数不适用、变量间不符合高斯分布甚至在进行多变量间相关性分析时，Copula熵依然适用，因此Copula熵在风电机组运行变量的相关性描述方面更具有优势。

3 分工况下各状态变量相关性分析

风电机组运行时，由于叶片桨距角、偏航角度和转矩等变量的变化，不同工况下的风电机组运行状态差异较大，所捕获的风能和产出的功率差异明显，各工况的变量相关性结果也存在一定的不同。实际工程中，对风电机组运行工况的划分是根据风电机组的设计特性与工程经验进行的，综合考虑各种因素，将风电机组的运行工况按启动区、风能最大捕获区、恒转速区、恒功率区、限功率区5 个工况进行聚类划分，再分别进行各工况下的变量相关性分析。

3.1 基于K-means的工况聚类分析

对风电机组工况进行分类可以直观地看出风电机组工况分布特点。但基于工程经验和设计特性的划分很难看出各个工况功率的边界。不考虑风电机组的运行特性，直接运用聚类分析对风电机组工况进行划分，其结果可能与风电机组的真实运行情况不符。综合考虑各种因素和特征属性后，运用K-means 算法对风电机组运行工况进行聚类分析。

聚类分析是指将物理或抽象对象的集合分为由类似对象组成的多个类的分类过程。按数据的相似性进行分类，分类后的类别称为簇。它是一种无监督的学习方式，在学习过程中不需要预先定义类或带类的标记，它通过自身算法分类成簇。Kmeans 算法是目前最经典的聚类算法［24］。基本思想是：按聚类个数K，把空间中所有数据对象进行聚类，靠各自中心点近的归为一类，后逐次迭代计算新的中心点并进行归类，直到各簇之间彼此差异最大。

风电机组在运行过程中，随着外界状态和控制条件的变化，不断切换工况，输出不同功率。风电机组的运行工况可以看成由一系列传感器信息构成的状态向量，其相似程度由不同状态向量间距离的远近程度来衡量，距离越近相似程度越高，距离越远，相似度越低。本文根据风电机组状态向量的聚类分析进行运行工况的划分。选取风电机组运行过程中具有代表性的传感器参数——风速构成的状态向量进行聚类分析。由于风速和功率的量纲不同，首先对风速和功率进行归一化处理，使其均分布在［0，1］之内。根据工程经验设聚类中心数目为5，以欧式距离作为度量，对聚类中心进行初始化操作，使用K-means 算法对风电机组工况进行聚类分析，效果如图4所示。

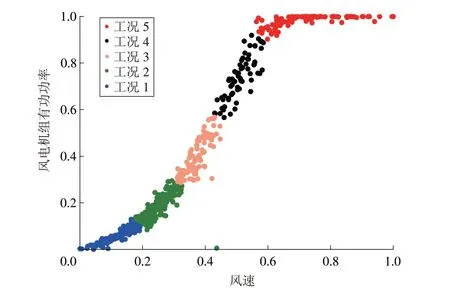
图4 风速和有功功率散点图工况聚类结果Fig.4 Clustering results of wind speed and active power scatter plots

由图4 可以看出，随着风速变化的功率符合工程经验，K-means 算法对工况的分类更准确，符合一般风电机组运行特性和工程经验。图4 中工况1为启动区，此时风速较小，风电机组产出功率较低；工况2 为风能最大捕获区，风速已满足风电机组运行所需最小风速，通过调整桨叶角度使风能捕获达到最大；工况3 是恒转速区，在较大风速下，风电机组内部传动系统达到额定转速，风电机组功率逐渐增大；工况4 为恒定功率区，风能稳定，功率达到额度功率，风电机组通过调整转速等方法减少风能捕获使风电机组功率状态稳定；工况5 为限功率区，风电机组出力达到自身上限，需要改变风电机组桨距角来减少风能的捕获，减小风电机组发电量，此时，虽然风速较大，但输出功率减小，小于额定功率。

不同工况下，风电机组运行特性不同，各状态变量间相关性强弱差异较大，对风电机组工况进行划分，研究不同工况下各状态变量间的相关性，能更准确地反映风电机组运行特性。

3.2 划分工况下变量相关性分析

根据章节2.2 的研究结论，Copula 熵在描述风电机组内部的变量相关性方面更具优越性，故这里选用Copula 熵对划分工况下的特征状态变量进行数理性分析，研究风电机组各变量间的耦合关系。经过计算，划分工况下不同状态变量的Copula 熵见表2。

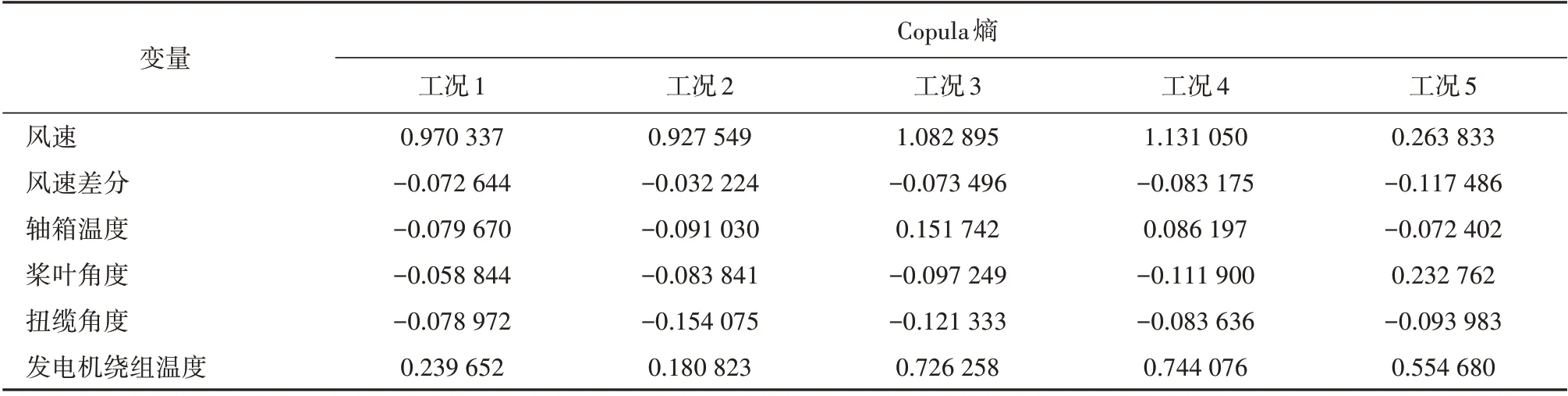
表2 划分工况下各状态变量与风电机组有功功率Copula熵Table 2 Copula entropy of each state variable and the active power of the wind turbine under the divided working conditions

根据表2 对各工况下的Copula 熵进行分析：工况1—4 下的风速与风电机组有功功率的相关性很强，而工况5下风速与风电机组有功功率无相关性；工况3—5 下发电机绕组温度与风电机组有功功率相关性较强，而在工况1 和工况2 下，发电机绕组温度与风电机组有功功率几乎无相关性；在工况1—5下，扭缆角度、桨叶角度和风速差分的Copula 熵小于0，三者和风电机组有功功率相关性很弱或几乎无相关性；工况3 和工况4 下的轴箱温度与风电机组有功功率中度相关，工况1、工况2 和工况5 的轴箱温度与风电机组有功功率几乎无相关性。分析结果与工况划分和发电机组运行特性相符。不同工况下风电机组运行特性差异较大，输出不同功率，各状态变量和风电机组有功功率相关性不同。

基于K-means 的工况划分下的特征状态变量相关性分析，能更精确地反映风电机组运行特性和不同状态下变量相关性强弱。因此针对不同工况的特征变量相关性研究更具有现实意义，在风电机组状态监测和功率预测方面更具有应用前景。

4 总结与展望

基于广东某海上风电场的SCADA 数据，对风电机组的各状态变量、工况和风速差分进行相关性研究，通过直观分析散点图变化规律，并进一步运用Copula 熵、Pearson 相关系数和Spearman 相关系数进行数理性分析，三者互相验证，表明Copula 熵在分析风电场状态变量与有功功率相关性研究方面更具有优势，在变量间不符合高斯分布以及进行多变量间相关性分析时，Copula 熵同样适用。针对不同工况下风电机组运行特性差异较大，采用K-means聚类分析对风电机组工况进行划分，并计算不同工况下相关状态变量的Copula 熵。研究表明，不同工况下各状态变量的相关性强弱各不相同，Copula 熵在描述变量相关性方面更准确且计算更简便。在未来风电场趋于大型化和集中化的背景下，不同工况的精确划分以及基于不同工况特征状态变量的相关性分析在风电资源合理利用、减少能源消耗方面更具有现实意义。