泵站侧向进水前池几何参数优化

李 明，王 勇,2，熊 伟，王哓林，刘厚林

泵站侧向进水前池几何参数优化

李 明1，王 勇1,2※，熊 伟1，王哓林1，刘厚林1

（1. 江苏大学流体机械工程技术研究中心，镇江 212013；2. 苏州工业职业技术学院精密制造工程系，苏州 215104）

为了减少泵站侧向进水结构内的不良流态，提高泵组运行效率，基于计算流体力学（Computational Fluid Dynamics，CFD）和响应面法（Response Surface Method，RSM）对泵站侧向进水前池进行几何参数优化。采用参数化设计对泵站侧向进水前池进行建模，通过与Workbench关联以对侧向进水前池的扩散角、坡度以及转向角实现指定值，采用典型Box-Behnke设计（Box-Behnke Design，BBD）方法得到17组三因素三水平试验方案，利用响应面法建立喇叭管出口断面流速分布均匀度与侧向进水前池扩散角、坡度以及转向角的回归方程，以最大出口断面流速分布均匀度为响应目标，确定最优参数组合，并将最优侧向进水结构的内部流动特性同原模型进行对比分析。研究结果表明，扩散角、坡度以及转向角对喇叭管出口断面流速分布均匀度具有显著影响（<0.05），扩散角与转向角的交互项对出口断面流速分布均匀度耦合作用显著，扩散角10°～13°、坡度8°～9°、转向角74°～75°时喇叭管出口断面流速分布均匀度达到最优。同原模型相比，优化后的侧向进水结构在设计水位下，断面流速分布均匀度至少提高23.41个百分点，流速加权平均偏流角提高13.95°，在低水位下断面流速分布均匀度至少提高18.30个百分点，流速加权平均偏流角提高14.79°，流道内没有偏斜流和大面积回流产生。该研究对于促进泵站侧向进水结构的优化设计具有一定的参考意义。

泵站；优化；数值模拟；侧向进水前池；流态；几何参数

0 引 言

泵站在跨流域调水、工农业用水、防洪排涝等方面发挥了巨大作用[1]。泵站进水结构包括进水前池和进水流道，进水前池作为衔接引水段和进水流道的关键装置，对于促进水流平稳、均匀地流至进水流道，提高泵组的运行效率具有重要意义[2]。泵站进水前池按照进水方式可以分为正向进水前池和侧向进水前池，受地理及施工条件的约束，往往采用侧向进水前池。相比于正向进水前池，水流在侧向进水前池内流动过程中方向会发生偏转，极易在转向过程中产生脱流和回流等不良流态[3-4]，导致水泵机组运行效率偏低，甚至会诱发不良振动、噪声等[5-7]。因此，对侧向进水前池进行优化设计，对于改善进水结构内的流态和提高泵组运行效率具有重要意义。

数值计算方法相对于试验方法具有成本低、效率高、易操作等明显优势，其在泵站进水结构优化以及内流分析方面，已经成为了一种不可或缺的手段。最初，国内外学者主要采用数值计算的方法对进水前池及进水流道内的复杂流态进行分析[8-12]，得到了内部流动规律及旋涡对流动稳定性的影响。随后，针对进水前池流态较差的问题，国内外学者采用数值模拟的方法研究了整流措施对前池内流态的影响，主要包括设置底坎[13]、设置压水板和配水孔[14-15]、导流栅[16]、导流墩[17-18]、导流柱[19-20]等，尽管以上措施已被证明对于提高进水前池流态稳定性具有显著效果，但是，这些措施大多采用增设辅助装置来改善流态，对于复杂的输水场景特别是施工空间有限时，适用性较差。对进水前池的关键几何参数进行优化，是解决上述问题的一个有效措施。Constantinescu等[21]采用-湍流模型和-湍流模型对比分析了具有壁面粗糙度的流道内涡的分布和强度，发现-湍流模型和低雷诺数-湍流对旋涡强度的预测结果基本保持一致，壁面粗糙度对边壁涡的影响较大。何婷婷等[22]基于VOF模型和RNG-湍流模型对开敞式进水池进行数值模拟研究，提出了一种能够有效地消除后壁旋涡的对称椭圆进水池后壁。资丹等[23]采用CFD和响应面相结合的方法对泵站进水前池的喇叭管悬空高度、与后壁距离和淹没深度进行优化设计，得到进水池的最优结构，通过流场计算发现，进水池内流态改善效果显著。Gao等[24]采用遗传算法和响应面法相结合的方法对双向流道结构进出口扩散段形状进行优化研究，结果发现优化后的双流道结构水力损失、流速不均匀程度和流量不均匀性程度均明显降低。响应面法能够充分考虑多因素对进水前池流态的影响，是一种准确且高效的优化方法，在侧向进水前池的多参数优化中表现出巨大的潜力[25]。

尽管国内外学者就泵站进水前池的优化展开了大量工作，然而，他们的研究大多集中在对泵站的正向进水前池进行优化，且大多数偏向于采用整流装置来改善流态，对于使用越来越广泛的多机组泵站的侧向进水前池几何参数优化研究还比较少，在这方面的优化经验还比较缺失。因此，本文针对多机组泵站的侧向进水前池几何参数进行优化，结合计算流体力学和响应面法对泵站侧向进水前池的扩散角、坡度和转向角进行优化研究，分析不同参数对泵站侧向进水结构内部流动特性的影响，并将优化模型和原模型的流场进行对比分析，以期为泵站侧向进水前池的优化设计提供一种高效的方法。

1 材料与方法

1.1 数值计算方法

1.1.1 计算模型

泵站侧向进水结构二维布置图如图1所示，该泵站包含3台容量50%的循环水泵，每台水泵均由独立的进水流道提供进水条件。泵站的设计水位H=7 m，最低水位H=6.5 m，循环水泵流量Q=8.76 m3/s，扬程H=26.0 m，循环水泵吸入口直径D=2 500 mm，设计最小淹没深度H=4.5 m。侧向进水前池扩散角为，坡度为，转向角为。侧向进水前池闸门和进水流道衔接处流态较为复杂，故将特征断面1设在此处；通常选取距进水喇叭管中心1.5（为喇叭管进口直径）处流态代表进水流道流态情况，故将特征断面2设于此处。

注：H1、H2、H3分别为距底面不同高度的断面，其距离底面高度分别为2.10、4.55和5.95 m。α、β、γ分别为扩散角、坡度、转向角。

1.1.2 计算域及边界条件

图2 侧向进水结构计算域

1.1.3 网格划分及无关性验证

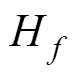
式中Hf为模型总水力损失，m；Pin为引水段进口断面总压，Pa；Pout为进水喇叭管出口断面总压，Pa；ρ为水的密度，kg/m3；g为重力加速度，m/s2。Hf随网格数变化趋势如图3所示。

随着网格数的增加，总水力损失总体上呈现下降趋势，当网格的数量超过790万后，水力损失变化幅度保持在5%以内，达到网格无关性分析的要求。为使计算效率提高，本计算在设计水位双泵运行工况下的计算域网格数量为950万。其他方案计算模型网格划分时也采用相同的网格尺度。

1.1.4 流态评价指标

1）流速分布均匀度

选用轴向流速分布均匀度来表征特征断面1、2轴向流速分布情况。其计算式如下：

2）流速加权平均偏流角

选用流速加权平均偏流角来表征喇叭管出口断面（泵进口断面）上横向流速角度分布情况。其计算式如下：

1.1.5 计算方案

在设计水位和低水位下，采用“两开一闭”的泵组运行方式，得到表1所示的计算方案。

表1 数值计算方案

注：1#、2#、3#表示泵序号。

Note: 1#, 2#, and 3# represent the pump number.

1.2 响应面法及因素水平选取

当侧向进水前池扩散角和转向角较大时，会导致水流进入转向段内侧流速升高，易在转向后发生脱流，在进入进水流道前形成回流，导致侧向进水前池流态恶化，而侧向进水结构转向段与扩散位置具有一定的坡度，在流入过程中，水流的过流面积不断增大，流速不断降低，在一定程度会抑制因转向段内侧的脱流现象，因此扩散角、转向角和坡度对侧向进水前池的流态具有明显影响。根据单因素模型试验得到的结果，当扩散角在10°～25°、坡度在6°～10°、转向角在65°～80°时，侧向进水结构回流和旋涡较少，因此以此范围作为自变量的最初取值范围。采用Box-Behnke设计（Box-Behnke Design，BBD）方法进行试验设计及后续分析，每个因素只能选择3个水平，分别为上限值、下限之及其中间值。试验因素及水平如表2所示。

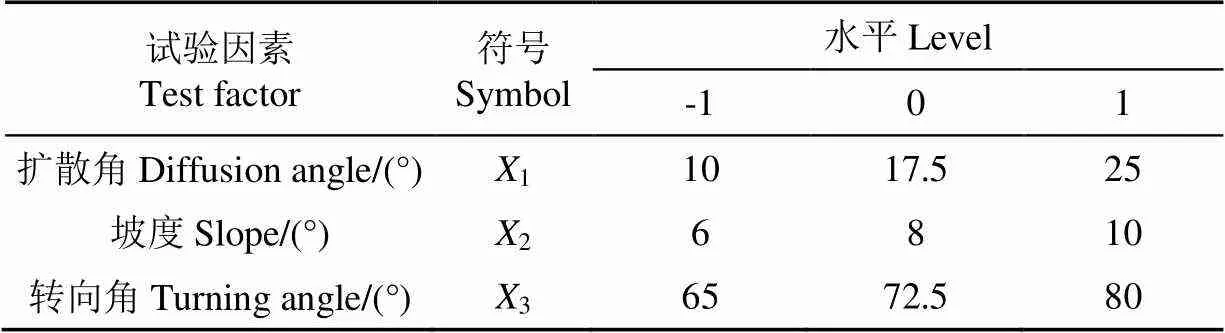
表2 试验因素及水平

2 结果与分析

2.1 数值计算结果验证

按照几何比尺1∶10搭建模型试验台对特征断面1各纵向测点的流速进行测量，在不同水位下进行多次试验并取平均值以消除偶然误差，引入相对误差值来表示数值计算与试验的误差。选择设计水位A1方案和低水位B1方案下的模型试验结果同数值计算结果进行对比分析。从表3可以看出，两方案1断面四层纵向测点的平均流速误差均在10%以内，说明计算方式基本符合泵站流道流动计算要求。从表4可以看出，两方案出口断面流速分布均匀度模型试验和数值计算误差均在5%以内，数值计算结果与模型试验结果基本一致，说明数值计算方法具有一定准确性。

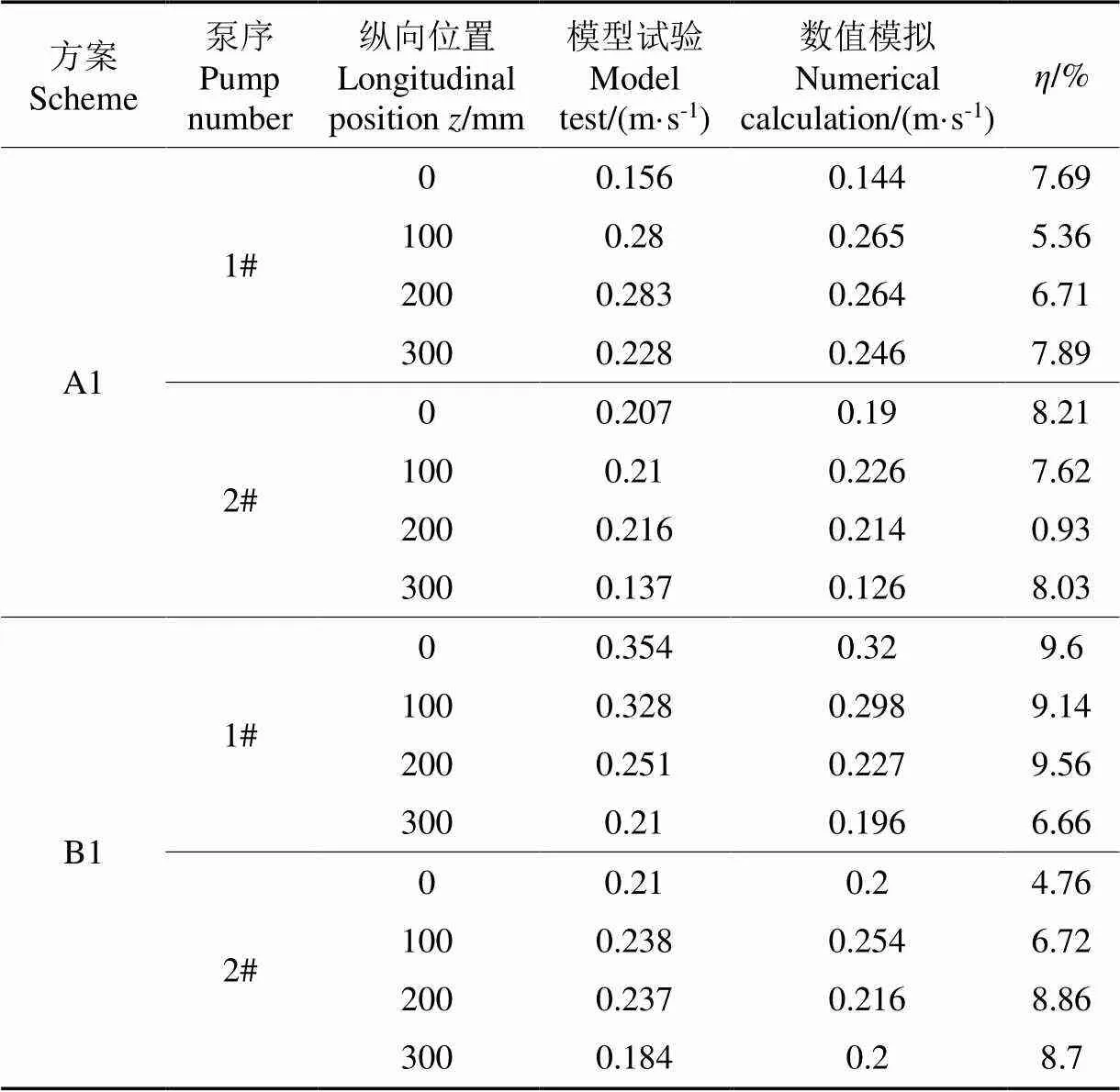
表3 C1断面纵向测点平均流速模型试验和数值计算误差

注：表示纵向测点距底面距离，为相对误差，下同。

Note:is the distance from the longitudinal measuring point to the bottom,is the relative error, the same below.

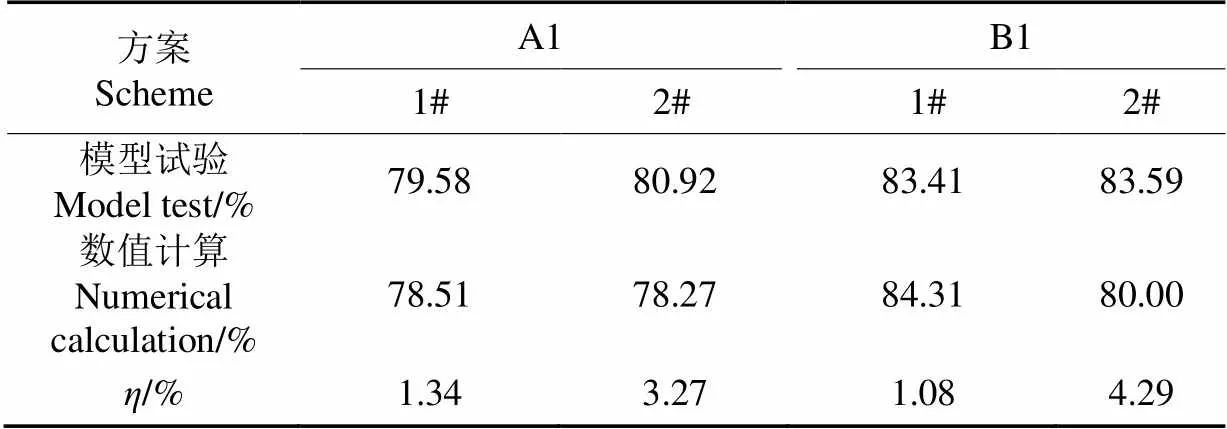
表4 C1断面流速分布均匀度模型试验和数值计算误差

2.2 响应面法优化结果

2.2.1 试验设计结果

选取A1方案的1#泵喇叭管出口断面流速分布均匀度为目标函数，BBD试验设计结果如表5所示。

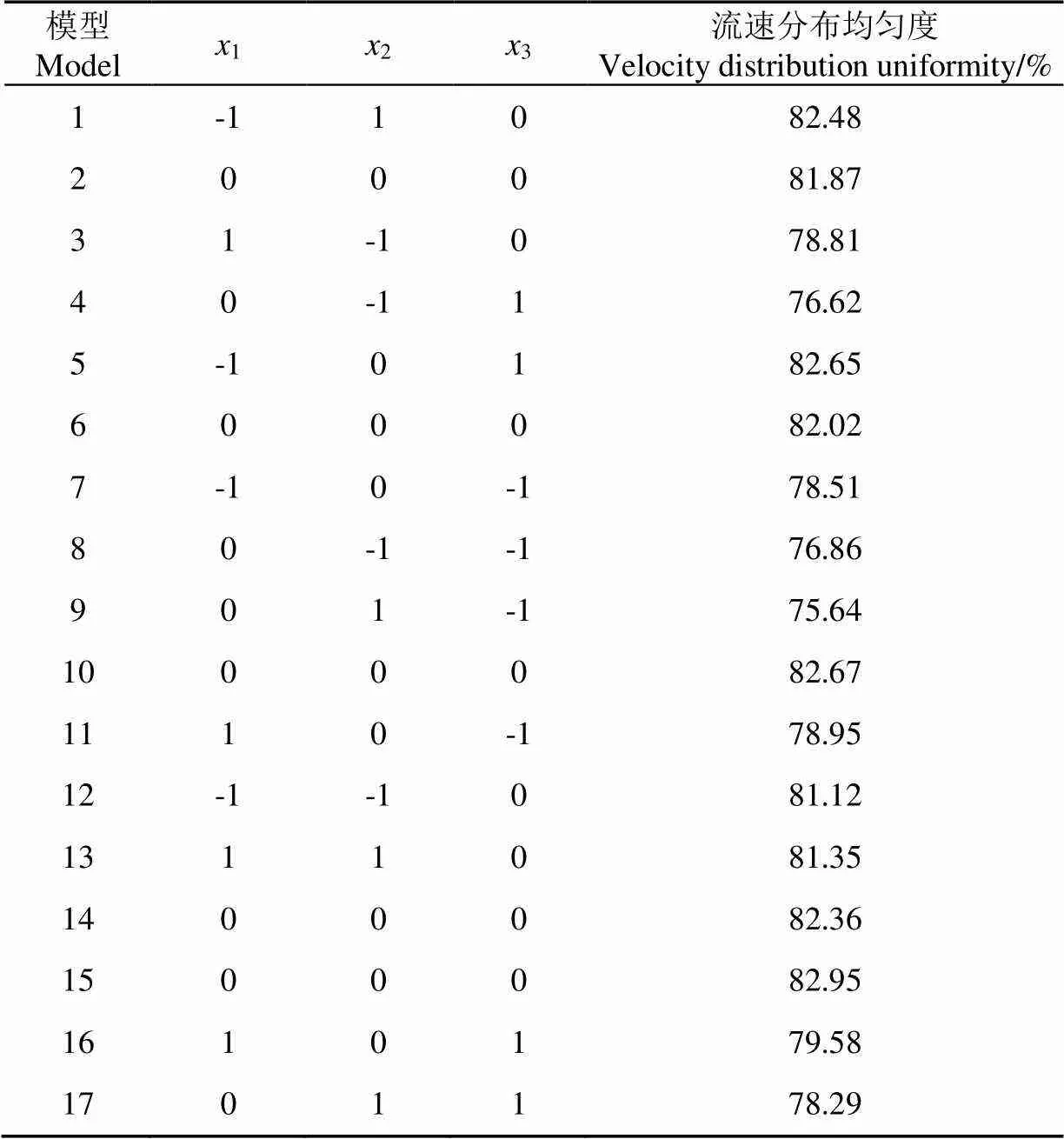
表5 BBD试验设计结果

注：1、2、3分别为因素1、2、3的水平值。

Note:1,2and3are the level values of factors1,2and3, respectively.

2.2.2 参数显著性分析

BBD试验设计方法是一种拟合响应曲面的二阶三水平设计，是利用含有二次项的方程来表征因子与响应值之间的关系。喇叭管出口断面流速分布均匀度的回归方程如下：

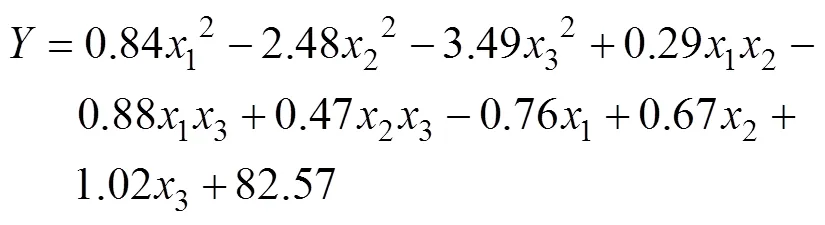
通过方差分析对回归方程进行分析，当<0.05时，则该项的差异性显著，<0.001时，则该项的差异性极其显著，>0.05时，则该项的差异性不显著。回归方程系数的显著性检验结果见表6，从表中可以看出，回归方程的值小于0.000 1，表明回归方程极其显著，能够很好地反映3个参数对出口断面流速分布均匀度的影响。1、2、3的值分别为0.004 8、0.009 0、0.000 9，均小于0.05，因此，扩散角、坡度、转向角都是显著影响因素，且单一几何参数对出口断面流速分布均匀度的影响程度从大到小依次为：转向角（3）、扩散角（1）、坡度（2）。

表6 出口断面流速分布均匀度方差分析结果

2.2.3 多因素作用分析

图4a为扩散角和坡度交互项对出口断面流速分布均匀度耦合影响的响应面图。由图可知，随着坡度的增加，喇叭管出口断面流速分布均匀度先增大后减小，随着扩散角的增加，出口断面流速分布均匀度逐渐减小。结合表6可知，扩散角与坡度的交互项对出口断面流速分布均匀度耦合作用不显著，扩散角对出口断面流速分布均匀度的影响比坡度更为显著，为了使出口断面流速分布均匀度最高，坡度应在8°～9°之间，扩散角应在10°～13°之间。图4b为坡度和转向角交互项对出口断面流速分布均匀度耦合影响的响应面图。由图可知，随着坡度和转向角的增加，出口断面流速分布均匀度均先增大后减小。结合表6可知，坡度与转向角的交互项对出口断面流速分布均匀度耦合作用不显著，转向角对出口断面流速分布均匀度的影响比坡度更为显著，为了使出口断面流速分布均匀度最高，转向角应在74°～75°之间。图4c为扩散角和转向角交互项对出口断面流速分布均匀度耦合影响的响应面图。从中可以发现，随着扩散角和转向角的增加，出口断面流速分布均匀度先增大后减小。结合表6可知，扩散角与转向角的交互项对出口断面流速分布均匀度耦合作用显著，转向角对出口断面流速分布均匀度的影响比扩散角更为显著，为了使出口断面流速分布均匀度最高，扩散角应在10°～13°之间。交互项对出口断面流速分布均匀度的影响程度从大到小依次为：扩散角和转向角的交互项（13）、坡度和转向角的交互项（23）、扩散角和坡度的交互项（12）。

最终，选择扩散角为11°、坡度为8°、转向角为75°的侧向进水前池进行内部流动特性分析。

图4 各因素作用对出口断面流速分布均匀度的影响

2.3 数值计算结果

2.3.1 设计水位优化模型数值计算结果

选择A1方案的流场计算结果进行设计水位下侧向进水结构优化前后流态差异分析。由图5可知，对于原模型，在1断面处，水流在进水流道侧壁和后墙的共同作用下形成了小尺度的旋涡结构，其余位置没有明显涡带，这是因为该断面离液面较远，流态相对稳定。在2断面处，转向段尾部和进水流道内部都出现了大尺度旋涡，这是因为2断面位于闸门下方，水流撞击闸门在闸门前产生了回流，此外，水流在闸门节流作用下速度增大，进入进水流道后来不及扩散，在闸门后形成一定尺度的旋涡。3断面离液面较近，回流和旋涡进一步加剧，这是因为液体表面的速度较大，容易产生表面涡，离液面越近，液下流动更容易受表面涡的影响，从而产生更大范围的回流和旋涡。经过优化后可以发现，各个断面相比于原模型流态稳定性大幅度提升，各断面均没有明显的严重偏流和大范围回流旋涡存在，喇叭管附近也无高强度的旋涡生成，而仅在部分断面靠近后墙位置以及闸门后方存在十分微弱的旋涡，这可能与固壁的影响有关。其余2个方案也有类似的结果。从表7也可以得出，原模型3种方案下1和2断面处的平均流速分布均匀度分别为53.65%和61.65%，特征断面流速分布均匀度较低，容易影响泵站稳定性及效率，经过优化后，特征断面1和2平均流速分布均匀度分别为78.67%和85.06%，分别提高了约25.02和23.41个百分点，流态显著改善，说明优化方法对于提高设计水位各方案下的流动稳定性具有明显效果。

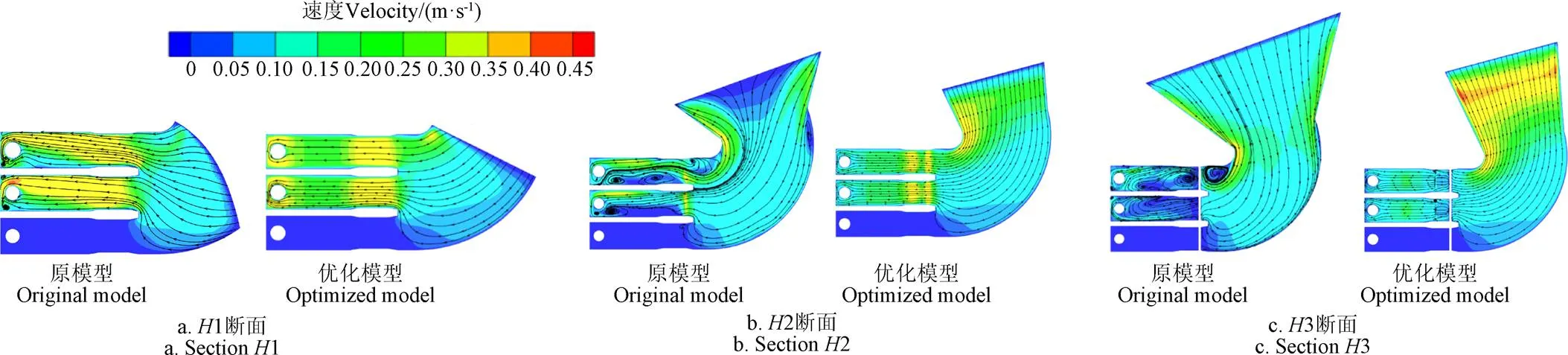
图5 A1方案特征断面速度分布

表7 设计水位下各运行方案断面流速均匀度

图6至图8为设计水位下3种方案喇叭管出口断面（泵进口断面）流速分布情况。由图可知，原模型中各泵组喇叭管出口断面流速分布总体呈现中间大四周小的趋势，且中高流速区域与中心位置均发生明显偏离，一定程度上降低了循环水泵的进水条件。模型优化后，各泵组喇叭管出口断面流速由中心向四周均匀减小，且中高流速区域基本同中心位置重合，能够为循环水泵提供良好的进水条件。从表8可知，原模型各运行方案喇叭管出口断面流速加权平均偏流角平均值为65.49°，模型优化后，各泵组运行方案喇叭管出口断面流速加权平均偏流角平均值为79.44°，比原模型提高了13.95°，水流稳定性明显提高，进一步说明该优化方法对于提高设计水位不同方案的流动稳定性具有明显效果。

图6 设计水位下A1方案喇叭管出口断面流速分布

图7 设计水位下A2方案喇叭管出口断面流速分布

图8 设计水位下A3方案喇叭管出口断面流速分布

表8 设计水位下各方案喇叭管出口断面流速加权平均偏流角

2.3.2 低水位优化模型数值计算结果

选择B1方案的流场计算结果进行低水位下侧向进水结构优化前后流态差异分析，如图9所示。同设计水位一样，对于原模型，随着断面高度的增加，大尺度旋涡、回流以及偏流现象更加明显，与之不同的是，这些旋涡的强度和尺度有所减小，这是因为坡度的存在会使得闸门承受一定水压，水位较高时，压力较大，水流通过阀门后扩散作用较强，在进水流道内产生高强度大尺度旋涡，水位较低时，闸门的埋入深度较小，水压更小，因此水流通过闸门后，其扩散作用也较弱，在进水流道内形成得旋涡强度和尺度都更小。模型优化后，侧向进水结构没有出现明显的偏流和大范围回流旋涡。其余两个方案也有类似的结果。从表9也可以看出，对于原模型，1和2断面的平均流速分布均匀度分别为55.14%和67.43%，比设计水位下的流速分布均匀度有所提高，经过优化后，1和2断面的平均流速分布均匀度分别为83.02%和85.73%，分别提高了27.88和18.30个百分点较于原模型显著提高，说明优化方法对于提高低水位工况各方案的流动稳定性也具有明显效果。

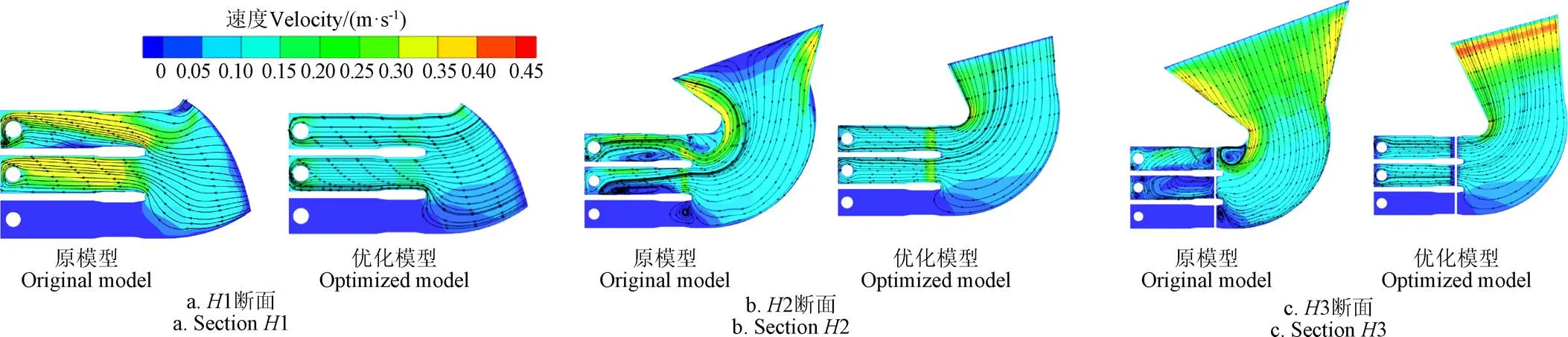
图9 B1方案特征断面速度分布

图10至图12为低水位工况下3种方案喇叭管出口断面流速分布情况。对于原模型，中间高流速区域与中心位置偏离程度较高，严重降低了循环水泵的水泵进水条件。模型优化后，B1和B3方案喇叭管出口断面流速分布均匀性极大提高，中高流速区域与中心位置重合，但是B2方案喇叭管出口断面四周出现小范围高速区，说明优化结果对该运行方案流态的改善效果不强，但是对于其他运行方案流态的改善效果十分明显。从表10可知，原模型各运行方案喇叭管出口断面流速加权平均偏流角平均值约为63.72°，优化后喇叭管出口断面流速加权平均偏流角平均值约为78.51°，平均增幅为14.79°，总体上改善较为明显，进一步说明优化方法对于提高低水位工况各方案的流动稳定性也具有一定效果。

表9 低水位下各运行方案断面流速分布均匀度

图10 低水位下B1方案喇叭管出口断面流速分布

图11 低水位下B2方案喇叭管出口断面流速分布

图12 低水位下B3方案喇叭管出口断面流速分布

表10 低水位下各方案喇叭管出口断面流速加权平均偏流角

3 结 论

本文基于计算流体力学和响应面法对泵站侧向进水前池关键几何参数进行了优化，并将优化后的侧向进水结构内部流动特性同原模型进行了对比分析，主要得到以下结论：

1）侧向进水前池扩散角、坡度、转向角都是影响侧向进水结构出口断面流速分布均匀度的重要参数，其对出口断面流速分布均匀度的影响程度从大到小依次为：转向角、扩散角、坡度。

2）为了使喇叭管出口断面流速分布均匀度达到最优，侧向进水前池扩散角应在10°～13°之间，坡度应在8°～9°之间，转向角应在74°～75°之间。

3）响应面优化结果对于改善设计水位和低水位下其他运行方案的流态也具有明显效果。在设计水位下，优化后的侧向进水结构在特征断面1和2处流速分布均匀度分别提高了约25.02和23.41个百分点，喇叭管出口断面加权偏流角提高了13.95°左右；在低水位下，优化后的侧向进水结构在特征断面1和2处流速分布均匀度分别提高了约27.88和18.30个百分点，喇叭管出口断面加权偏流角提高了14.79°左右，优化后的侧向进水结构没有偏斜流和大面积回流产生，水力性能明显提升。

[1] Kong Y, Kong Z, Liu Z, et al. Pumped storage power stations in China: The past, the present, and the future[J]. Renewable & Sustainable Energy Reviews, 2017, 71: 720-731.

[2] Gustavo A, Mutasem E F. Effects of approach flow conditions on pump sump design[J]. Journal of Hydraulic Engineering, 1996, 122(9): 489-494.

[3] 高传昌，曾新乐，解克宇，等. 泵站进水池超低水位下组合整流方案与验证[J]. 农业工程学报，2017，33(23)：101-108.

Gao Chuanchang, Zeng Xinle, Xie Keyu, et al. Combined rectification scheme of pump intake sump in ultra-low water level and its verification[J]. Transactions of the Chinese Society for Agricultural Engineering (Transactions of the CSAE), 2017, 33(23): 101-108. (in Chinese with English abstract)

[4] Zhang H, Shi W D, Chen B, et al. Experimental study of flow field in interference area between impeller and guide vane of axial flow pump[J]. Journal of Hydrodynamics, Ser. B, 2015, 26(6): 894-901.

[5] Kim C G, Kim B H, Bang B H, et al. Experimental and CFD analysis for prediction of vortex and swirl angle in the pump sump station model[A]//IOP Conference Series: Materials Science and Engineering[C]. Macau, China: 4th Global Conference on Materials Science and Engineering, 2015, 72(4): 42-44.

[6] Fockert A D, Westende J M C V, Verhaart F I H, et al. Automatic swirl angle measurements for pump intake design[J]. Journal of Hydraulic Research/Journal de Recherches Hydraulique, 2015, 53(3): 384-393.

[7] Sotoudeh N, Maddahian R, Cervantes M J. Investigation of Rotating Vortex Rope formation during load variation in a Francis turbine draft tube[J]. Renewable Energy, 2015, 7(2): 547086.

[8] Yang F, Liu C. Numerical and experimental investigations of vortex flows and vortex suppression schemes in the intake passage of pumping system[J]. Advances in Mechanical Engineering, 2015(2).

[9] 蒋红樱，成立，颜红勤，等. 不同形状的泵站封闭式进水池喇叭口水力性能模拟与验证[J]. 农业工程学报，2016，32(13)：31-35.

Jiang Hongying, Cheng Li, Yan Hongqin, et al. Simulation and validation of hydraulic performance of closed-style pump sump with different bell-mouth shapes[J]. Transactions of the Chinese Society for Agricultural Engineering (Transactions of the CSAE), 2016, 32(13): 31-35. (in Chinese with English abstract)

[10] Cheng B, Yu Y. CFD simulation and optimization for lateral diversion and intake pumping stations[J]. Procedia Engineering, 2012, 28: 122-127.

[11] 资丹，王本宏，王福军，等. 开机组合对泵站进水系统泥沙浓度分布的影响[J]. 农业工程学报，2022，38(7)：59-68.

Zi Dan, Wang Benhong, Wang Fujun, et al. Influence of start-up pump units on the sediment concentration for the intake system of a pumping station[J]. Transactions of the Chinese Society for Agricultural Engineering (Transactions of the CSAE), 2022, 38(7): 59-68. (in Chinese with English abstract)

[12] Huang X, Guo Q, Qiu B, et al. Prediction of air-entrained vortex in pump sump: Influence of turbulence models and interface-tracking methods[J]. Journal of Hydraulic Engineering, 2020, 146(4): 04020010.

[13] 李志祥，冯建刚，钱尚拓，等. 排水泵站整流底坎参数优化[J]. 农业工程学报，2021，37(3)：56-63.

Li Zhixiang, Feng Jiangang, Qian Shangtuo, et al. Optimization of rectification bottom sill parameters in drainage pumping stations[J]. Transactions of the Chinese Society for Agricultural Engineering (Transactions of the CSAE), 2021, 37(3): 56-63. (in Chinese with English abstract)

[14] 徐存东，王国霞，刘辉，等. 大型泵站正向前池防淤优化模拟研究[J]. 武汉大学学报（工学版），2018，51(7)：577-588.

Xu Cundong, Wang Guoxia, Liu Hui, et al. Simulation study of preventing sedimentation in front inflow forebay at large-scale pumping station[J]. Engineering Journal of Wuhan University, 2018, 51(7): 577-588. (in Chinese with English abstract)

[15] 葛新峰，冯源，郑源，等. 侧向进水泵站配水孔数模优化[J]. 水利水电技术，2010，41(3)：59-63.

Ge Xinfeng, Feng Yuan, Zheng Yuan, et al. Numerical model based optimization on distribution hole of pumping station with side inlet[J]. Water Resources and Hydropower Engineering, 2010, 41(3): 59-63. (in Chinese with English abstract)

[16] 徐捷，施伟，袁寿其，等. 基于Star CCM+的闸站上游流道方案设计与数值模拟[J]. 排灌机械工程学报，2021，39(1)：37-43.

Xu Jie, Shi Wei, Yuan Shouqi, et al. Design and numerical simulation of upstream channel in sluice-pumping station based on Star-CCM+[J]. Journal of Drainage and Irrigation Machinery, 2021, 39(1): 37-43. (in Chinese with English abstract)

[17] 徐磊，夏斌，施伟，等.中隔墩长度对斜式轴伸泵装置出水流道水力特性的影响[J]. 农业工程学报，2020，36(1)：74-81.

Xu Lei, Xia Bin, Shi Wei, et al. Influence of middle pier lengths on hydraulic characteristic of outlet conduit in pump system with slanted extension shaft[J]. Transactions of the Chinese Society for Agricultural Engineering (Transactions of the CSAE), 2020, 36(1): 74-81. (in Chinese with English abstract)

[18] 资丹，王福军，姚志峰，等. 大型泵站进水流场组合式导流墩整流效果分析[J]. 农业工程学报，2015，31(16)：71-77.

Zi Dan, Wang Fujun, Yao Zhifeng, et al. Effects analysis on rectifying intake flow field for large scale pumping station with combined diversion[J]. Transactions of the Chinese Society for Agricultural Engineering (Transactions of the CSAE), 2015, 31(16): 71-77. (in Chinese with English abstract)

[19] 李颜雁，郭鹏程，孙龙刚，等. 立柱对大型泵站前池和进水池流态影响的数值分析[J]. 排灌机械工程学报，2021，39(9)：929-936.

Li Yanyan, Guo Pengcheng, Sun Longgang, et al. Numerical analysis on influence of vertical column on flow pattern in forebay and intake of large pumping station[J]. Journal of Drainage and Irrigation Machinery, 2021, 39(9): 929-936. (in Chinese with English abstract)

[20] 营佳玮，俞晓东，贺蔚，等. 基于流体体积模型的泵站前池流态及组合式整流方案[J]. 排灌机械工程学报，2020，38(5)：476-480，493.

Ying Jiawei, Yu Xiaodong, He Wei, et al. Volume of fluid model-based flow pattern in forebay pump sump station and combined rectification scheme[J]. Journal of Drainage and Irrigation Machinery, 2020, 38(5): 476-480, 493. (in Chinese with English abstract)

[21] Constantinescu G S, Patel V C. Role of turbulence model in prediction of pump-bay vortices[J]. Journal of Hydraulic Engineering, 2000, 126(5): 387-391.

[22] 何婷婷，史志鹏，张涛，等. 基于CFD的泵站开敞式进水池后壁形状的优化设计[J]. 中国农村水利水电，2013(6)：85-87.

He Tingting, Shi Zhipeng, Zhang Tao, et al. Optimization and design of the after-wall shape about open pump sump on CFD[J]. China Rural Water and Hydropower, 2013(6): 85-87. (in Chinese with English abstract)

[23] 资丹，王福军，姚志峰，等. 基于响应曲面模型的泵站进水池参数优化方法研究[J]. 水利学报，2017，48(5)：594-607.

Zi Dan, Wang Fujun, Yao Zhifeng, et al. Research on optimization method of pump sump parameters based on response surface model[J]. Journal of Hydraulic Engineering, 2017, 48(5): 594-607. (in Chinese with English abstract)

[24] Gao X, Tian Y, Sun B. Multi-objecive optimization design of bidirectional flow passage components using RSM and NSGA: A case study of inlet/outlet diffusion segement in pumped storage power station[J]. Renewable Energy, 2018, 115: 999-1013.

[25] 徐颖. 基于响应面法的侧向进水泵站前池整流措施研究[D]. 扬州：扬州大学，2021.

Xu Ying. Research on Rectification Measures for Forebay Side-inlet Pumping Station based on Response Surface Method[D]. Yangzhou: Yangzhou University, 2021.

[26] Tsan-Hsing S, WilliaW L, Aamir S. A new-eddy viscosity model for high Reynolds number turbulent flows: Model development and validation[J]. Computers & Fluids, 1995, 24(3): 227-238.

[27] 张校文，刘超，荣迎春，等.多机组泵站正向进水阵列式隔板整流模拟及试验验证[J].排灌机械工程学报，2022， 40(4)：378-384.

Zhang Xiaoyou, Liu Chao, Rong Yingchun, et al. Numerical simulation and experimental verification of forward feed array diaphragm rectifier for multi-unit pumping station[J]. Journal of Drainage and Irrigation Machinery Engineering, 2022, 40(4): 378-384. (in Chinese with English abstract)

[28] 刘志泉，成立，卜舸，等. 泵站正向进水前池“V”形导流墩整流数值模拟[J].中国农村水利水电，2022，(3)：183-188.

Liu Zhiquan, Cheng Li, Bu Ge, et al. Numerical simulation of V-shaped diversion pier for improving the flow pattern in forward inlet forebay of the pumping station[J]. China Rural Water and Hydropower, 2022, (3):183-188. (in Chinese with English abstract)

Optimizing the geometric parameters for the lateral inflow forebay of the pump sump

Li Ming1, Wang Yong1,2※, Xiong Wei1, Wang Xiaolin1, Liu Houlin1

(1.,,212013,;2.215104)

Lateral inflow forebay is inevitably utilized to connect the diversion and inlet passage in water transport engineering, because of geographical and construction constraints. However, the flow in the lateral inlet forebay is very easy to generate undesirable flow patterns (such as the flow separation and backflow) leading to vibration and low operating efficiency. In this study, the geometric parameters were optimized for the lateral inlet forebay of the pump sump using Computational Fluid Dynamics (CFD) and Response Surface Method (RSM), in order to improve the flow pattern for the high efficiency of the pump unit. Firstly, the parametric design was realized for the lateral inflow forebay of the pump sump using the 3D modeling software NX 10.0. There were the specified parameters associated with the Workbench, such as the diffusion angle, slope, and turning angleof the lateral inlet forebay. Secondly, the typical Box-Behnke Design (BBD) was selected to determine the three factors and three levels test. 17 groups of test schemes were obtained to simulate the flow field of the lateral inlet structure under the Fluent platform. Thirdly, the optimization target was selected as the uniformity of velocity distribution at the horn tube outlet section. The second-order polynomial regression equation was utilized to establish the regression equation of velocity distribution uniformity at the horn tube outlet section and geometric parameters, namely the diffusion angle, slope, and turning angleof the lateral inlet forebay. Subsequently, the significance of the regression equation was evaluated by the analysis of variance. As such, the regression equation reflected the relationship between the response values and factors. The maximum uniformity of velocity distribution at the outlet section was selected as the response target to determine the optimal parameter combination. Finally, the internal flow characteristics of the optimal lateral inlet structure were compared with the original model, including the uniformity of velocity distribution and the velocity-weighted average drift angle. Results indicate that there was a significant influence of the diffusion angle, slope, and turning angleon the velocity distribution uniformity at the horn tube outlet section. Among them, the most significant was the turning angle, whereas, the less significant was the slope. Furthermore, there was no significance of the slope, and the turning angleon the coupling effect of velocity distribution uniformity at the outlet section. By contrast, the diffusion angle and turning angle posed the most significance on the coupled uniformity of velocity distribution at the outlet section, in terms of the interaction between the diffusion angleand slope. Moreover, there was the greatest influence of the interaction between the diffusion angleand the turning angle. But, the least influence was found in the interaction between the diffusion angleand the slope. An optimal uniformity of the velocity distribution was achieved at the horn tube outlet section under the lateral inlet forebay with the diffusion angleof 10°-13°, the slopeof 8°-9°, and the turning angleof 74°-75°. Compared with the original model, the cross-sectional velocity distribution uniformity of the optimized lateral inlet structure under design water level increased by 23.41 percentage points at least, and the velocity-weighted average drift angle increased by 13.95°, similarly, under low water level, the cross-sectional velocity distribution uniformity of the optimized lateral inlet structure increased by 18.30 percentage points at least, and the velocity-weighted average drift angle increased by 14.79°. More importantly, there was no deflected flow and large-area reflux in the channel. These findings can provide the positive significance to promote an optimal design of the lateral inlet structure of the pump sump.

pump station; optimization; numerical simulation; lateral inlet forebay; flow pattern; geometric parameter

10.11975/j.issn.1002-6819.2022.19.008

TV675

A

1002-6819(2022)-19-0069-09

李明，王勇，熊伟，等. 泵站侧向进水前池几何参数优化[J]. 农业工程学报，2022，38(19)：69-77.doi：10.11975/j.issn.1002-6819.2022.19.008 http://www.tcsae.org

Li Ming, Wang Yong, Xiong Wei, et al. Optimizing the geometric parameters for the lateral inflow forebay of the pump sump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(19): 69-77. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.19.008 http://www.tcsae.org

2022-08-01

2022-09-28

国家自然科学基金资助项目（51979126）

李明，研究方向为水力空化技术及其应用。Email：2293372963@qq.com

王勇，博士，研究员，博士生导师，研究方向为水力机械空化机理及特性。Email：wylq@ujs.cn