相互渗透，交叉作用——论初中数学教学中数形结合思想的应用

◎谢荣君 （临沂第十四中学，山东 临沂 276000）

一、前 言

数形结合，简单来说就是数、形之间的相互转化.数学知识相对抽象，教师通过数形结合思想可以让学生更好地理解数学知识，有助于学生构建完整的数学知识结构.数形结合思想还能促进学生的知识迁移，强化学生数学思维的发展，这对学生的数学核心素养发展十分有利.因此，在日常教学中，教师应注重学生数形结合思想的培养.

二、数形结合思想在初中数学教学中的作用

在初中数学教学中，教师落实数形结合思想具有十分重要的意义，其主要表现如下：

（1）促使学生形成完整的数学概念.为了方便学生对数学概念的理解，当前的初中数学教材省略了概念生成过程，这就使很多学生在学习概念时，只能通过死记硬背的方式进行记忆，这使他们难以深层次地理解数学概念的内涵，学习压力比较大.实际上，初中数学有很多概念知识都是可以在实际生活中找到相关模型的，教师可以通过数形结合的方式，将这些模型的图片呈现到课堂上，让学生对其进行分析思考，促使学生在直观的模型中感知到数学的意义，体会数学概念的价值，帮助学生把握概念知识本质，提升学生学习效果.

（2）优化学生数学认知结构.数学认知结构是学生在数学学习中形成的知识结构模型，也是学生内化数学知识的体现.在初中数学教学中，教师可以借助数形结合的方式，帮助学生将数学知识有序地整合在一起，促使学生系统化、整体化地学习知识，便于学生全面归纳知识，从而为学生解决数学问题提供良好的理论支撑.

（3）提高学生的数学学习兴趣.由于数学知识内容多、理解难度较大，不少学生对数学产生畏难情绪，特别是对于函数这类比较抽象的数学知识，学生纷纷表示单靠自己的想象和已有的知识经验，很难准确掌握.数学结合思想可以将这些函数或方程以清晰、形象的坐标系或图形的形式展示出来，将复杂的知识简单化，从而使学生好理解、好掌握，自然减轻对数学学习的畏难情绪，增强数学学习兴趣.

（4）提高学生分析问题、解决问题的能力.在解决数学问题的过程中，学生常常会陷入题干所给出的已知条件中，找不出解决问题的方法，容易出现面对函数问题只会依靠函数知识去解题，面对几何问题只能调动几何知识去解题的情况，实际上换一种思路往往会有“柳暗花明又一村”的感觉，而数形结合思想就是拐点.学生将数学结合思想渗透进题干已知条件之中，用形助数，用数解形，将数与形相结合，就可以用方程、不等式或函数解决有关几何的问题，也可以用函数图像或几何图形来解决有关函数或方程的问题，从而将复杂的问题转变成简单的问题，找到解决问题的关键.因此，在教学中，教师应用数学结合思想引导学生找出数与形的契合点，有效培养学生分析问题、解决问题的能力.

三、初中数学教学中应用数形结合思想的原则

在初中数学教学中，教师应用数形结合思想时，应该按照相应的原则进行，这样才能获得好的教学效果.

首先，要坚持直观性原则.对于初中学生来说，他们的认知活动是以形象的事物、思维为出发点的.教师通过形象的方式将抽象的数学内容呈现出来，有助于学生深层次地理解问题.在数形结合思想中，“形”是通过直观的几何图形来描述数学元素之间的数量关系的，属于图像表征.初中数学教师在教学中渗透数形结合思想时贯彻直观性原则，能让学生更加简捷地处理问题，并且能促进学生思维转化.

其次，要坚持循序渐进原则.初中学生在学习知识时，是从感性层次逐渐上升到理性层次的.教师在渗透数形结合思想时，应该坚持循序渐进原则，根据学生的认知，合理地设计教学活动，指引学生对知识进行逐层探索，为学生的良好发展提供保障.

最后，要坚持反复渗透原则.学生的学习并不是简单地增长知识数量，而是其在自身现有知识的基础上不断重新构建、组织.因此，教师在教学中需要在不同的阶段逐渐渗透数形结合思想，引导学生不断扩充知识，并让学生主动应用数形结合思想.学生在获取新知识时，会结合自身的认知、发展需求对其进行反复理解、巩固.数形结合思想是不可见的概括性知识.学生在理解数形结合思想时，需要从简单到复杂，这就需要教师进行反复渗透.

四、初中数学教学中数形结合思想的应用策略

（一）以形助数

在数形结合中，以形助数，简单来说就是通过形象、具体的几何图像对抽象、复杂的数量问题进行处理，借助图像的性质来简单处理抽象的代数问题.

例如，已知正实数a、b、c、d同时满足两个等式：a2＋b2＝c2和求证：ab＝cd.

由题干给出的已知条件：a2＋b2＝c2和以及勾股定理的逆定理，我们可以将题干给出的数式构造成图形，画出直角三角形和直角三角形斜边上的高，即Rt△ABC，∠ACB＝90°，作CD⊥AB于点D，可以得出BC＝a，AC＝b，AB＝c，CD＝d.经过计算得出ab＝cd，于是解出这道题的正确答案.

这道题就是典型的以形助数，通过将题干中给出的“数”的性质和特点转化成相对的“形”，使抽象的数量关系以清晰、直观的图形形式展示出来，从而用简单的几何方法解决了复杂的代数问题.

再如，小红从O沿直线匀速穿过类似抛物线的拱桥达到C（如图1所示），假设小红在10 s 与26 s 的位置高度相同，那么小红骑车从O到达C需要多长时间？

图1

在这个问题中，学生是很难根据题意直接计算出答案的，因此教师可以引导学生对题目中给出的图形进行分析.学生经过观察可以看出题目中给出的拱桥图像就是一个抛物线，其解析式是y＝ax2＋bx.根据题目信息，小红在10 s 与26 s 所处的位置高度是一样的.假设小红在10 s 达到A点，在26 s 达到B点，如图2所示，以此为依据找出抛物线的对称轴.在此基础上，教师引导学生根据抛物线的对称性计算出小红从O到达C需要的时间.

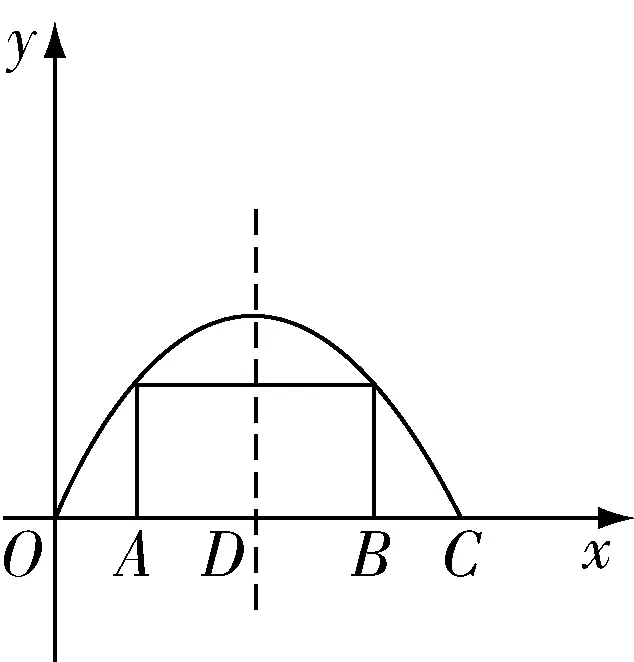
图2

由于A到B的时间为26－10＝16 s，D是AB线段的中点，因此A到D所需时间为8 s，即从O到达D的时间是10＋8＝18 s.根据抛物线的对称性可以得出从O到达C的时间是2×18＝36 s.

在本题中，教师引导学生从已有的知识结构入手，让学生将类似抛物线的拱桥看作一个抛物线，然后将拱桥问题转变成已经学过的抛物线问题，结合抛物线图像、性质完成求解.在此过程中，学生需要用数形结合思想将抽象的代数问题转变成具体的几何问题，这对学生解题准确性的提升很有利.

（二）以数解形

在数形结合中，以数解形，简单来说就是通过对几何图像进行认真观察、分析，找出其中的数量关系，借助代数来处理几何图像问题.

例如，已知△ABC，D是△ABC边BC上的点，E是△ABC边AB上的点，连接AD和EC，使得△ABD和△ACD的周长相等，同时△CAE和△CBE的周长也相等.设BC＝a，AC＝b，AB＝c.求AE和BD的长.

在解答这道题时，我们通过题干中的已知条件“△ABD和△ACD的周长相等，同时△CAE和△CBE的周长也相等”可以写出两组等式，再采取化简和等量代换的方式就可以求出AE和BD的长.

解答这道题就是运用了数学结合思想中以数解形的方法，虽然题干中给出的已知条件是比较形象的图形，但是对于图形的定量条件还是必须依靠代数来解决，从而实现无逻辑性的图形通过转化成为相对应的数，使图形更清晰，更富有逻辑.

再如，某三角形的三个外角比是2 ∶3 ∶3，试判断该三角形的形状.

我们对本题进行分析可以看出，其虽然是几何体，但是在解题中应用几何方法是难以得出结论的，因此教师可以引导学生尝试用代数的方式来解题.

我们可以设三角形的三个外角分别是2x、3x、3x，由于三角形的外角和是360°，可以得出2x＋3x＋3x＝360°，x＝45°，从而得出三角形的三个外角分别是90°、135°、135°，由此判定三角形的三个内角分别是90°、45°、45°，得出该三角形是等腰直角三角形.

在本题中，教师可引导学生对题目给出的信息进行分析，找出相关数量关系.在解题过程中，我们以三角形外角为背景，结合数形结合思想，可以很好地将几何问题转变成代数问题，这对学生解决问题十分有利.

（三）数形互助

数形互助强调代数与几何的深入结合，使复杂问题能得到简单处理.在处理一些复杂、综合的问题时，教师可以引导学生通过数形互助的方式来完成解题，从而简化学生的解题过程.

例如，如图3所示，在△ABC中，AB＝5 cm、BC＝7 cm，∠B为直角.线段AB上，有一个点P从A点出发，按照1 cm／s 的速度向B运动；线段BC上，有一个点Q从B点出发，按照2 cm／s 的速度向C运动.问：（1）假设点P与点Q同时从A、B出发，经过多长时间△PBQ的面积是4 cm2？（2）假设点P与点Q同时从A、B出发，经过多长时间PQ的长度是5 cm？ （3）在第一个问题中，△PBQ的面积是否可以等于7 cm2？

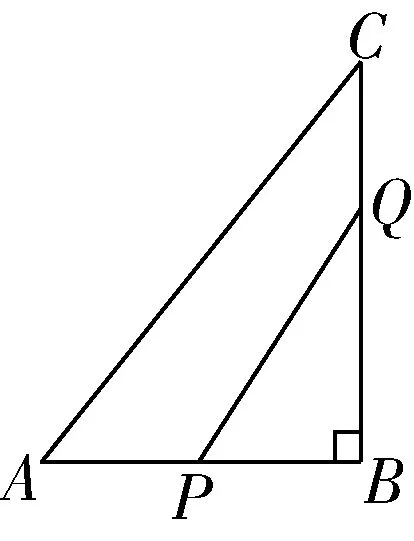
图3

在本题中，教师可以引导学生通过数形互助的方式来处理问题，促使学生更深层次地应用数形结合思想，强化学生对数形结合思想的认识.

（1）假设经过xs 以后△PBQ的面积是4 cm2，结合题意可以知道P＝xcm，BQ＝2xcm，AB＝5 cm，PB＝（5－x）cm，由于△PBQ的面积是4 cm2，∠B＝90°，得出x）×2x＝4，得出x1＝1，x2＝4，对此结果进行论证，当x＝4 时，2x＝8，即BQ＝8 cm，但是题目中BC＝7 cm，不符合题意，因此得出x＝1，即点P与点Q同时从A、B出发，经过1 s 后△PBQ的面积是4 cm2.

（2）假设经过xs 后PQ＝5 cm，结合题意可以知道，AP＝xcm，BQ＝2xcm，AB＝5 cm，PB＝（5－x）cm，在Rt△PBQ中，根据勾股定理得出PB2＋BQ2＝PQ2，即（5－x）2＋（2x）2＝25，得出x1＝2，x2＝0，从而得出x＝2，即点P与点Q同时从A、B出发，经过2 s 后PB长度是5 cm.

（3）假设经过xs 以后△PBQ的面积是7 cm2，与（1）相同得出（5－x）×2x＝7，由于Δ＝25－28＜0，该方程无解，因此判断△PBQ的面积无法等于7 cm2.

教师在渗透数形结合思想时，要特别注意数形之间的等价转化，要保证图形的精准性、完整性，要保证绘图符合实际情况，这样才能避免出错.

（四）在归纳、总结中渗透数形结合思想

在初中数学教学中，教师渗透数形结合思想时应该结合具体的内容进行.同一种数学思想在不同学段、单元的呈现是比较分散的，没有什么规律.因此，在教学中，教师需要在每一章、每一单元的归纳、总结中渗透数形结合思想，让学生可以系统地感知数学内容，强化学生对数形结合思想的感悟.例如，正比例函数、一次函数、反比例函数知识比较分散，每个部分的知识学习都需要融入数形结合思想，并且这些函数之间既有区别，又有联系，学生在学习中容易混淆，因此教师需要在教学中不停、反复地指导学生归纳，让学生可以在归纳中加深对数形结合思想的认识.初中数学教师在日常教学中必须意识到，数形结合思想的渗透一方面需要在课堂上进行，另一方面需要指引学生树立良好的意识，增强数感，从而引导学生养成好的学习习惯.

五、总 结

在数学教学中，数形结合思想是一种十分常见的思想观念.初中数学教师应注意学生数形结合思想的培养，指引学生灵活应用数形结合思想来解决数学问题.这样不仅可以锤炼学生的数学思维能力，还能让学生对数量关系、空间形式有更好的感知，有助于学生数学学习水平的提升，促进学生数学核心素养的提升.