寻图形之关联,研图形之题根
——以“一线三等角”题根图形为例
文/华南理工大学附属实验学校 广州市黄埔区开元学校 王雅华
“一线三等角”是初中几何教学中一种常见的题根图形,其本质是在一条直线上有三个相等的角.在初一阶段,学生初识全等三角形时,常见三直角的顶点在一条直线上,随着难虔的增加,这三个直角可能是相等的锐角或钝角,全等形进一步转化为相似形.有些试题,“一线三等角”直接跃然纸上,让人一望而知.有些试题,“一线三等角”隐藏于复杂图形之后,需要抽丝剥茧或添加辅助线构建而知.无论“显”或“隐”,均需要学生在掌握基本的题根图形后,能够熟练辨析这其中的“变”或“不变”,从而增强学生对“一线三等角”的识别能力和应用能力.
一、题根呈现,引发思考
如图1、2,在ΔABC中,∠ABC=∠ADB=∠BEC,若AB=BC,则△ADB≌△BEC.

图1
解析:当∠ABC=∠ADB=∠BEC=90°时(如图1),我们看到这三个直角的顶点D、B、E均在同一条直线上,通过AB=BC,易得△ADB≌△BEC(AAS),从而可推导出一些线段对应相等,如AD=BE,BD=CE(或DE=AD+CE)等.
当∠ABC=∠ADB=∠BEC≠90°时(如图2),虽然这三个相等的角的虔数在不断地变化,但是永恒不变的是它们的顶点依旧在同一条直线上,再满足条件AB=BC,始终都可得出ΔADB≌ΔBEC(AAS),这就是“一线三等角”之全等形的题根图形.
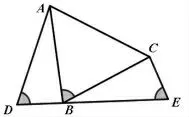
图2
变式1:如图3、4,在ΔABC中,∠ABC=∠ADB=∠BEC,若AB≠BC,则△ADB∽△BEC.

图3
解析:此变式题目为例1中全等题根延伸后对应的“一线三等角”之相似形的题根图形,当AB≠BC时,呈现的是全等和相似之间的关联与不同,形状相同,大小不同,即△ADB∽△BEC(AA),进而推导出对应线段成比例
变式2:在ΔABC中,当DE绕着点B旋转时,若∠ADF=∠CEF=∠ABC且AB=BC时,有△ADB≌△BEC(图5);若∠ABC=∠ADB=∠BEC且AB≠BC时,有△ADB∽△BEC(图6).

图5

图6
解析:通过旋转变换,使得三个相等的角被某条直线错开(其中有一个角被分开,另外两个角在直线的两侧),引发学生思考,此题所得出的结论同样可通过推导角证明.
上述所呈现的是典型的“一线三等角”题根图形,可分为同侧和异侧两种类型,无论哪种类型,它的本质特点均为:三个相等角的顶点在同一条直线上.随着角虔的不断变化或者其中角绕着其顶点旋转一定的角虔,往往会形成很多美观和谐的图形,且结论都成立.因此,近年来各地命题专家都命制了很多可用“一线三等角”题根图形的结论来进一步求解的中考试题,大都体现了学生在学习过程中应不断提升其几何直观、推理才能和模型思想等素养.
二、试题呈现,魅力题根
例1.如图7,四边形ABCD中,对角线AC与BD交于点O,且OA

图7
(1)求证:四边形ABCD是正方形;
(2)若H是边AB上一点(H与A,B不重合),连接DH,将线段DH绕点H顺时针旋转90°,得到线段HE,过点E分别作BC及AB延长线的垂线,垂足分别为F,G.设四边形BGEF的面积为S1,以HB,BC为邻边的矩形的面积为S2,且S1=S2.当AB=2时,求AH的长.
思路简述:(1)问主要考察通过对角线所满足的条件四边形ABCD是正方形.
(2)由(1)问知四边形ABCD是正方形,且EF⊥BC,EG⊥AG,所以有∠G=∠EFB=∠FBG=90°,即证四边形BGEF是矩形.由DH旋转得DH=HE,∠DHE=90°,所 以∠ADH=∠GHE,通过“一线三等角”之全等形题根图形可证△ADH≌△GHE(AAS),所以AD=GH,再由AB=AD,导出四边形BGEF是正方形.设AH=x,则BG=EG=x,由S1=S2建立方程x2=2(2-x),进而-1(舍),即
评注:本题选自2020年玉林市中考第25题,此题蕴含着“一线三等角”之全等形的题根图形(图1),(1)问易通过对角线的关系得证;(2)问中关键句之“将线段DH绕点H顺时针旋转90°”为题根图形的存在提供了条件.
例2.如图8和图9,在△ABC中,点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB-BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.

图8

图9
(1)当点P在BC上时,求点P与点A的最短距离;
(2)若点P在MB上,且PQ将ΔABC的面积分成上下4:5两部分时,求MP的长;
(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);
(4)在点P处设计并安装一扫描器,按定角∠APQ扫描ΔAPQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若请直接写出点K被扫描到的总时长.
思路简述:(1)问考察知识内容为垂线段最短,因此作AS⊥BC交BC于点S,利用三角函数得出AS=3.

图10

图11


评注:本题选自2020年河北省中考第26题,(3)(4)问中点P在3<x≤9(设点P的运动路程为x)这段运动过程中,始终有∠APQ=∠B=∠C,这是典型的“一线三等角”之相似形的题根图形(图4),即在点P在此运动的过程中,始终有ΔABP∽ΔPCQ.

图4
以上两道例题所呈现的背景不同,但是所隐含的“一线三等角”题根图形的条件却一目了然,解法不言而喻.这两道题着重考察学生的几何直观、推理才能及题根运用的思想和能力.



图12
【拓展】如图13所示,在EG上取点M,使∠BME=∠AFE,过点C作CN//BM,交EG的延长线于点N,则∠N=∠BMG,再根据∠AEB+∠DEC=180°,∠EFA=∠AEB,推出∠EAF=∠BEM,从而△AEF∽△EBM,由相似三角形的性质得出又因为∠AEB+∠DEC=180°,∠EFA+∠DFE=180°,且∠EFA=∠AEB,所 以∠CED=∠EFD,而∠BMG+∠BME=180°和条件∠EFD+∠EDF+∠FED=∠FED+∠DEC+∠CEN=180°共同推出∠N=∠EFD,和∠EDF=∠CEN,故证明△DEF∽△ECN,则结合已知条件故有BM=CN,再证明△BGM≌△CGN(AAS),由全等三角形的性质可得证.

图13
评注:本题选自2020年江苏省宿迁市中考第27题,本题是在“一线三等角”之相似形的题根图形(4)的基础上构建三角形相似关系,提取线段比例式,进而解题的拓展应用.添加辅助线因题而异,虽无一个通法可循,但一般都能从题目中找到一定的规律和常用方法来构建我们熟知的题根图形,然后和题根图形的特征相比较,我们就可以利用题根的结论去创造更有利的条件,从而使问题得到顺利解答.
总之,针对这类表现背景不同,但却可用同一类基本题根求解的试题,就要求学生充分挖掘试题的内在价值,学会从复杂的图形中提取题根图形,灵活运用基本结论思考拓展.而且通过题根解题,能更好地弄清问题的本质,为解决问题搭建好思维的“脚手架”,进而切实可行地提高学生的解题能力,真正实现学生数学素养的提升.

