基于DTW-K-means 模型的银行地产股价波动聚类分析

吴忠睿 吴金旺 邬华阳

一、文献综述

在迈向第二个百年奋斗目标、实现共同富裕的征途中，国富民强是我们追求的最终目标，对家庭来说，财富的保值和增值是最可靠的保障。中国社科院国家金融与发展实验室、中国社科院金融研究所和中国社会科学出版社发布的《中国国家资产负债表2020》显示，在总的社会财富中，政府部门达到162.8万亿元,占总财富的24%；居民部门达到512.6 万亿元，占总财富的76%，居民人均财富约为36.6 万元。从1984年第一家上市公司上海飞乐音响上市开始，经过近40年的发展，中国股市经历了从最初的雏形到逐渐发展壮大的过程。股票投资已经成为居民理财的重要组成部分，截至到2022年7月末，个人投资者开户数超2 亿户。

金融是现代经济的核心，与经济共生共荣，承担着自身高质量发展和为实体经济纾难解困的双重责任。在我国金融体系中，银行业居于主体地位，银行间接融资成为大量中小微企业融资的主要渠道。银行业优质公司也纷纷谋求上市，补充资本金，提高风险抵御能力，扩大社会影响力。截止2021年12月31日，沪深AB 股上市企业中，共有41 家银行，总市值达93318 亿元。尽管数量少，但是盈利能力强，银行股已成为资本市场的“压舱石”。在我国土地国有和城市化、工业化背景下，房地产兼具金融属性和商品属性，已成为居民投资的“热土”。个人住房贷款是服务居民的一个重要渠道，个人住房贷款的增长一方面使得居民负债增加，另一方面也催生了房地产泡沫，成为中国系统性金融风险的重要来源，因此已成为宏观审慎监管的重要对象。对于地方政府来说，逐步转向“基建投资”为依托的“土地金融”模式，代价就是地方政府的高负债和高房价。由于缺乏实体经济的支撑，当前的“以地融资”风险越来越大，空间越来越小。下行波动是风险的重要体现，通过波动聚类可以发现银企之间的深层关系，特别是风险聚集关系，当前这方面的研究还较为缺乏。

杨子晖等（2018）研究发现，在2015年“熔断机制”事件中，房地产与证券部门成为风险传染的网络中心[1]。蔡真（2018）从房地产部门与银行体系的外在关联性、房地产部门与地方政府债务的关联性以及高房价背景下资本外逃压力三个方面，阐明房地产市场已经成为系统性金融风险的重要监测领域[2]。我国系统性金融风险经由房地产市场传染有三个途径：房价大幅下跌后的风险传染途径、房企贷款违约后的风险连锁传染途径、影子银行信用链条断裂后的“多米诺骨牌”式风险传染途径。白鹤祥等（2020）运用2006-2017年16 家上市银行数据测度了我国房价大幅下跌所引发的系统性金融风险，并构建了基于房地产市场的系统性金融风险预警指标[3]。朱恩伟等（2019）对2009-2014年间我国238 家房地产上市公司与19 家主要内资银行之间的银企关系进行度量（以百度新闻为语料来源，在新闻中共同出现则意味着关联），发现良好的银企关系能显著提高企业的信贷可得性[4]。

商业银行与房地产公司之间通过资产负债表、信贷业务等渠道形成复杂的网络关系。当某一机构受到外部冲击引发债务违约时，流动性风险通过业务关联的信贷渠道传染，其他机构都将受到风险溢出的影响。所以如何衡量机构之间的关联性是一个复杂问题，有的机构虽然业务规模大，但是对其他机构影响有限，更多起到抵御风险的作用；有的机构虽然业务规模不大，但与其他机构连接较多、较深，成为风险传染的中心，需要重点关注。如何发现这种关联性？在机器学习的视阈下，可以通过大数据技术方法，聚类出波动特征类似的股票。聚类本质上是集合划分问题，通过指定的距离计算（即相似度计算），将相似的数据尽可能地划分至同一簇（应尽可能地使不同簇的数据有较大区别）。金融数据的聚类大都基于特征值进行，如刘沩玮（2010）使用分层聚类法分析37 家创业板上市公司[5]；张康林等（2021）使用自组织特征映射（SOM）法对股票进行特征聚类[6]。但是，这只能体现数据特征的相关性，不能体现股价的时序性和历史相关性，不适合在时间序列数据中使用。Warren Liao, T（2005）认为聚类技术可以基于原始数据、特征值或模型进行，基于原始数据的聚类方法可以体现数据的原始特征，基于原始数据模型是通过修改聚类算法中的距离测量方法实现的[7]。Berndt, D.J.和J. Clifford（1994）、Paparrizos, J.和L.Gravano（2015）提出，动态时间规划（DTW）可以计算时间序列相似度（即距离）[8,9]；Chen 等（2022）将K-means 模型距离计算方法修改为DTW，并以中国16 家上市商业银行为研究对象，根据收盘价的时序数据进行聚类，找出走势相似的银行[10]。

在金融行业，风险具有明显的传染特征。如何衡量风险的传染特征，一直是研究的重点。在构建投资组合、金融市场风险管理和各类衍生产品定价的过程中，波动率是一个常用的指标。波动包括正向波动和负向波动，风险主要是下行的波动率，也就是下跌的部分。波动率包括隐含波动率和实际波动率，其中隐含波动率代表风险中性世界对未来波动率的预期，可以使用期权定价模型来估计。假定市场符合理性预期，就可以用实际波动率代替现实世界对未来波动率的预期[11]。宫晓莉和熊熊（2020）基于DCC-GARCH 刻画股市波动率，形成动态相关关系，并构建股市波动率指数与其他市场波动率指数的投资组合，发现房地产波动率指数是对冲股票波动率指数的有效工具[12]。

在现有文献中，通过大数据方法对波动聚类的研究相对较少。张康林等（2021）使用SOM 按特征对股票进行聚类，但只能体现股票特征的相关性，不能反映历史（即时序）的相关性，也未体现波动的特征[6]。由于不是对基于时间序列的原始数据进行聚类，因此时间序列的原本特征丢失。苏木亚（2017)采用谱聚类（Spectral Clustering）方法对全球主要股市波动率进行聚类分析，但谱聚类不能体现时间序列的原始走势特征，同时聚类结果取决于相似矩阵，不同的相似矩阵结果可能不同[13]。

本文的创新点在于：首先，对已实现波动率进行聚类分析，发现连接性强的银行和房地产企业。其次，通过DTW-K-means 聚类波动率的时间序列，可以分析数据的原始走势特征，继而为投资者决策提供依据，也为监管部门系统掌握机构聚集关系提供新的视角。

二、聚类指标构建

（一）欧式距离计算

欧式距离用来计算两个相同长度时间序列的距离。对于时间序列=(x1,…,xm)和=(y1,…,ym)，他们的欧氏距离ED 定义如下：

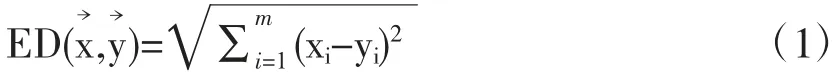
（二） 动态时间规划DTW（Dynamic Time Warping）

DTW 可以对两个时间序列找到最优的非线性对齐。对于时间序列和，DTW距离的计算过程如下：首先用x→和y→这两个时间序列构建m×n 的矩阵M，矩阵中的第(i,j)项代表时间序列数据点xi和yj的欧式距离；然后找到一条穿过矩阵的规划路径使得累计欧氏距离和最小，规划路径W=w1,w2…wk，W 中的元素代表x→中的第i 个点和y→中的第j 个点的欧氏距离；最后找到最小累计（见公式2）。

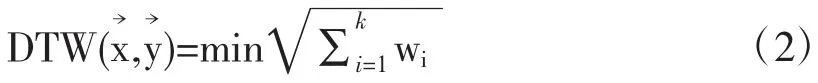
矩阵M 上的最优路径可以使用如下递归函数计算：

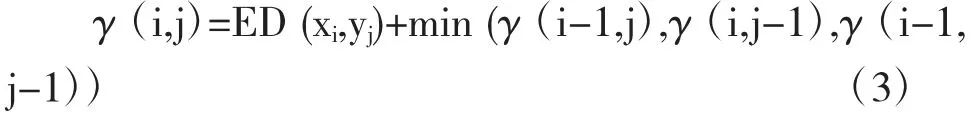
通过对比发现，欧式距离的相似度计算简单方便，时间复杂度较低，但欧式距离无法检查时间轴上的位移。动态时间规划DTW 则可以很好地解决此问题，代价是提升了时间复杂度。本文将使用DTW作为相似度计算算法，并采用LB_Keogh 下界法来提升运算速度。

（三）DTW-K-meams 算法

基于原始数据的方法主要是修改聚类算法的距离或相似度计算方法以适应时间序列，可以保持原始数据最原始的特征。基于特征值型和基于模型主要是通过提取时间序列特征值和转换时间序列原始数据使得参数可以适用于模型。本文主要使用基于原始数据进行聚类的方法，通过修改K-meams 的距离算法以适应时间序列。

给定数据集D={x1,x2…,xm},将其聚为k 个簇（k根据需要设定）；c={C1,C2…,Ck}，c 是每个簇中心的集合。K-means 的目标函数如公式（4）所示，过程是先计算每个序列到其对应簇的中心序列的DTW 距离，然后将距离累加求和。

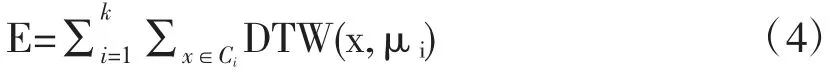
其中，μi为Ci的中心，根据动态时间扭曲重心平均（DBA）计算。

具体步骤如下：第一步，随机选择k 个样本作为初始的中心μi；第二步，根据每个样本到中心点μi的距离（使用DTW 计算）将样本划到最近的簇；第三步，重新使用DBA 计算每个簇的新中心μi；第四步，重复第二步和第三步直到每个簇的中心不再变化。

三、实证分析

（一）数据来源

本文以中国主要上市商业银行和房地产公司为研究对象，分别选取2010年前上市的16 家商业银行，其中大型商业银行5 家：建设银行，交通银行，工商银行，中国银行，农业银行；股份制商业银行8 家：华夏银行，民生银行，平安银行，浦发银行，兴业银行，招商银行，中信银行，光大银行；城市商业银行3家：北京银行，南京银行，宁波银行。房地产公司选择市值靠前的万科A、保利发展、华侨城A、金地集团、绿地控股、ST 基础、广宇发展、陆家嘴、上海临港等9 家房地产公司。基于数据完整性和可得性，选取时间从2010年8月19日至2019年9月16日, 共计72,025 个高频数据。对于在这期间有停牌的股票，采用最后停牌价填充。高频数据采用python 的baostock 库通过api 接口方式获取。实证环境为python，版本为3.7.6。使用的第三方库有baostock，numpy，pandas，matplotlib，tslearn，sklearn 等。

（二）银行-房地产股价波动率计算

Bollerslev（1986)提出的GARCH 模型能很好地刻画金融资产收益率的异方差性和波动聚集效应、非对称效应，为分析时间序列提供了更有针对性的方法。该模型形式简单，包括了均值模型和方差模型，在实践中不断得到扩展和应用，比如与动态相关系数、Copula 函数等结合。传统的GARCH 类模型基于相同的采样频率,以日数据为主。而随着高频数据的获取越来越容易，大量学者在波动率模型中加入能及时反映信息的高频数据。研究显示，高频数据可以提高波动率模型的预测能力。Andersen 和Bollerslev（1998)研究指出，由日内高频收益率平方和得到已实现波动率，结果具有无偏性和稳定性特征，且计算简便，是波动率的一种较为理想的替代变量。已实现波动率通常基于5 分钟，原因在于当数据频率过高时，容易受到各类噪声交易的干扰，不能反映共性特征；而当数据频率过低时，则会丧失个性特征，估计精度会降低。每5 分钟采样一次可以有效抵消市场微观结构噪声的影响。

为了便于对比分析，本文采用对数差分的方法计算5 分钟的对数收益率，计算公式为。已实现波动率用RV 表示，计算方法见公式（5）。

由于不同股票的价格变化区间不一致，因此在进行聚类或预测前，需要消除量纲的影响，一般采用标准化处理或归一化处理的方式。在对原始数据做处理时，本文使用常用的均值-方差标准化方式，计算公式如下：

（三）波动相关性分析

从相关系数的计算结果看，银行间的相关系数普遍较高，120 对相关系数全部都在0.6 以上，平均值高达0.75。房地产企业与银行间的相关性，除保利发展、万科A、金地集团外，其余企业与银行的相关性普遍较低，平均值只有0.39，房地产企业间的两两相关性也普遍不高，平均值只有0.34。相关系数最高的是华夏银行和光大银行，为0.85，最低的是交通银行和ST 基础，接近于0。研究发现，ST 基础与其他所有企业相关性都不高。原始样本显示，ST 基础在样本期内共有305 天停牌。为验证ST 基础和其它企业的低相关性是否由长时间停牌造成，本文在剔除所有股票停牌日期后，再计算两两相关性，发现ST 基础与其它所有企业相关性依旧不高，最高0.32，最低0.11。这说明ST 基础波动表现出显著的异质性，其波动几乎不受银行和房地产影响。

从相关性分析可以看出，银行间的相关系数较大，房地产企业间的相关性普遍较低，仅头部房地产企业间或头部房地产企业与银行间的相关系数较大。这说明银行间的关联较密切，主要通过支付结算、直接或间接持有共同资产或互相购买对方资产产生较强的关联。而房地产企业和银行的关联主要来自银行的房地产贷款，而银行的房地产贷款中头部房地产企业占比较大，这是头部企业关联关系较大的原因。

（四）商业银行及房地产股价波动聚类分析

本文使用K-means 对25 家银行和房地产企业已实现波动率进行聚类。另外，将时间序列相似度即距离算法修改为DTW。其中K 是聚类簇数，实验中分别设置为2-6。结果如图1 及表1 所示。

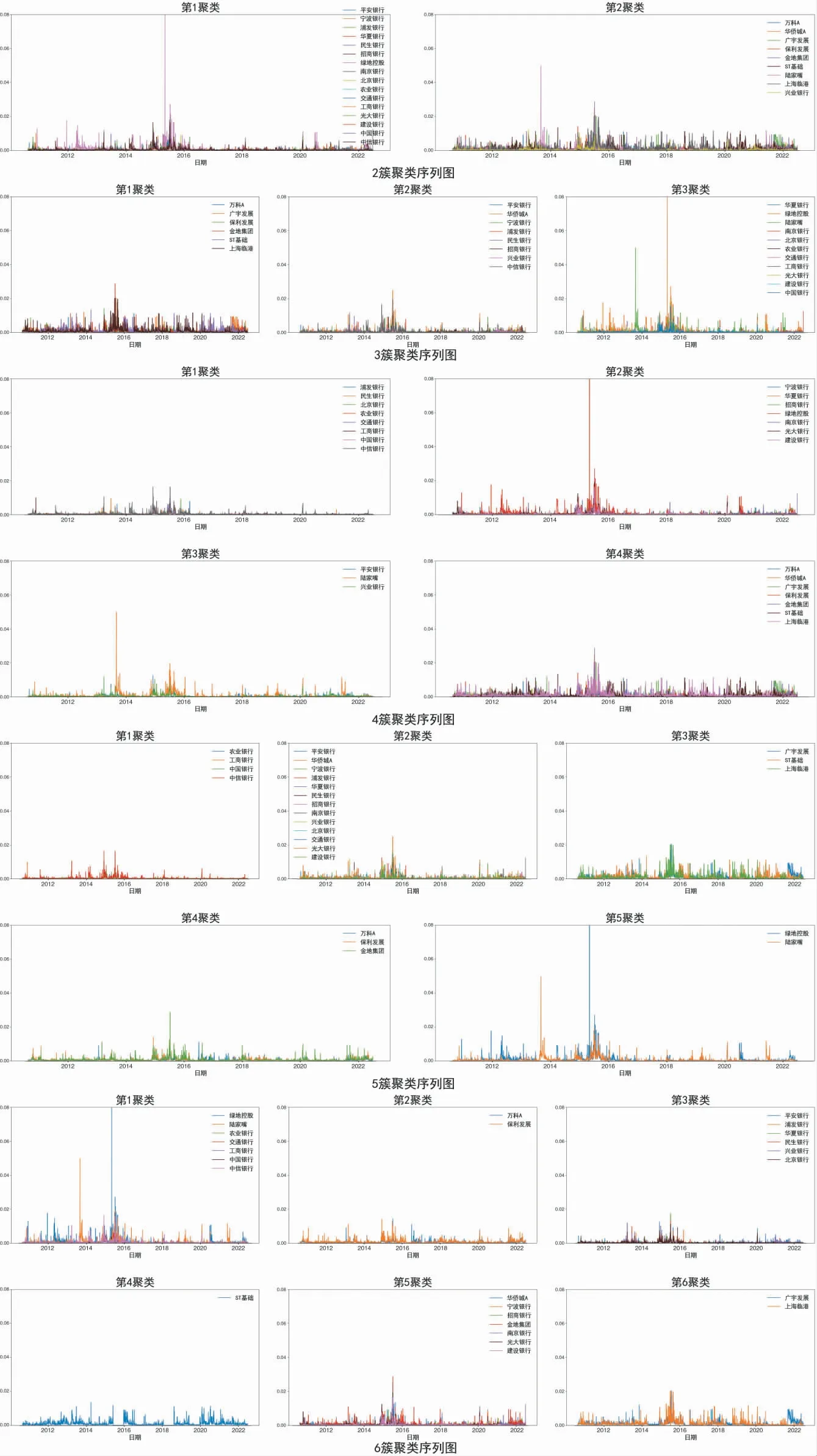
图1 聚类序列图

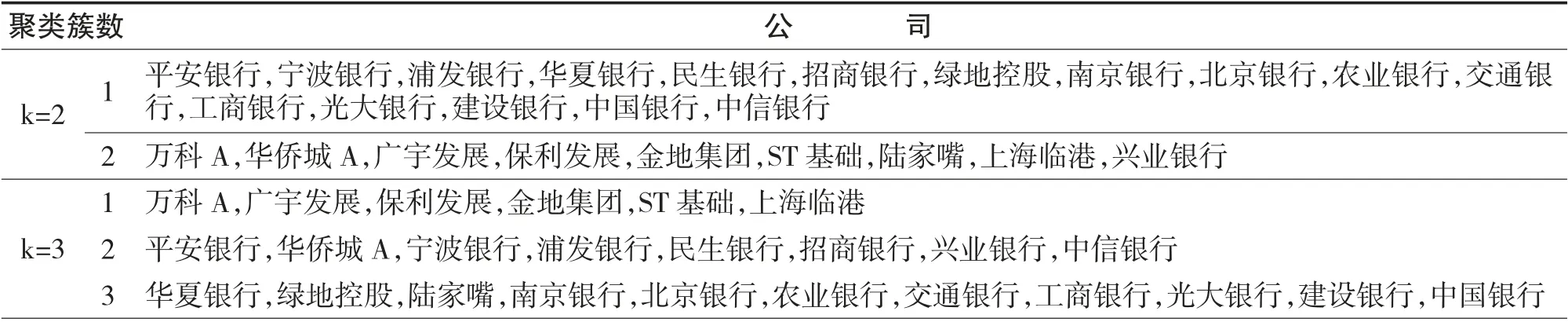
表1 波动聚类结果（k=2-6）

1浦发银行，民生银行，北京银行，农业银行，交通银行，工商银行，中国银行，中信银行k=4 2 宁波银行，华夏银行，招商银行，绿地控股，南京银行，光大银行，建设银行3 平安银行，陆家嘴，兴业银行4 万科A，华侨城A，广宇发展，保利发展，金地集团，ST 基础，上海临港1农业银行，工商银行，中国银行，中信银行k=5 2 平安银行，华侨城A，宁波银行，浦发银行，华夏银行，民生银行，招商银行，南京银行，兴业银行，北京银行，交通银行，光大银行，建设银行3 广宇发展，ST 基础，上海临港4 万科A，保利发展，金地集团5 绿地控股，陆家嘴k=6 1 绿地控股，陆家嘴，农业银行，交通银行，工商银行，中国银行，中信银行2 万科A，保利发展3 平安银行，浦发银行，华夏银行，民生银行，兴业银行，北京银行4 ST 基础5 华侨城A，宁波银行，招商银行，金地集团，南京银行，光大银行，建设银行6 广宇发展，上海临港

从聚类结果可以发现，波动呈现出明显的聚集效应。从2 簇聚类的结果可以看出，银行和房地产两个板块波动聚集效应明显，簇1 除了绿地控股外都为银行，簇2 除了兴业银行外都为房地产企业。簇1整体波动幅度小于簇2，整体波动频率亦低于簇2，表明银行板块波动相对稳定，房地产具有高波动性，可以分别作为稳健投资和风险投资对象。农业银行、工商银行、中国银行等无论分为几簇，在聚类中始终聚在一起，具有高度的波动一致性，通过图1 可以发现其波动最为稳定，体现出大型国有商业银行相对保守的风险应对策略，是真正的“压舱石”，风险抵御能力强，适合承担系统重要性金融机构职责。同时在股份制银行中，浦发银行、民生银行也始终聚在一起，波动具有高度一致性。通过图1 可发现，它们的波动大于大型国有商业银行，具有一些剧烈波动点。比如在2013-2014年钱荒期间和2015-2016年股灾期间，由于两家银行都为股份制商业银行，因此在风险策略上较为开放，导致波动加大，可能更易受到极端风险冲击。对于房地产企业，在6 簇聚类中除了金地集团被单列（可能聚类数量过多划分过于精细），万科A、保利发展、金地集团始终聚在一起，波动具有高度一致性。通过图1 发现，它们具有较高的波动频率但整体振幅小于其它房地产企业。较高的波动频率和房地产的周期性发展相关，而低于其它房地产企业振幅说明它们发展较为稳定，抗风险能力优于其它房地产企业。将银行与房地产合在一起分析发现，绿地集团经常与银行聚在一起，其波动较为稳定，这是其与银行聚在一起的主要原因，同时发现它也有剧烈波动的情况，如2015年期间发生的重大波动远超其它银行和房地产企业，说明绿地集团正常情况下发展稳定，但是抵御风险的能力较弱。同样发现，一些银行会经常与房地产企业聚在一起，如平安银行和兴业银行，除了在6 簇聚类中没有和房地产企业一起，其余聚类结果中都有和房地产企业聚为一类，招商银行在所有聚类中都有和房地产企业聚在一起的现象。这一现象是否是由于银行对房地产行业的贷款业务占比过高所造成，还需做进一步探讨。

表2 为16 家银行2012-2021年房地产行业公司贷款占所有公司贷款比重。从表中可以看出，经常与房地产聚在一起的银行近10年平均占比较高，且排名靠前，如平安银行近10年平均占比19.78%，排名第一，兴业银行近10年平均占比13.83%，排名第六，招商银行近10年平均占比15.06%，排名第三。从数据分析可以看出，较高的房地产业贷款占比会使银行和房地产的波动关联性加强，相互影响更大，风险更易传染。

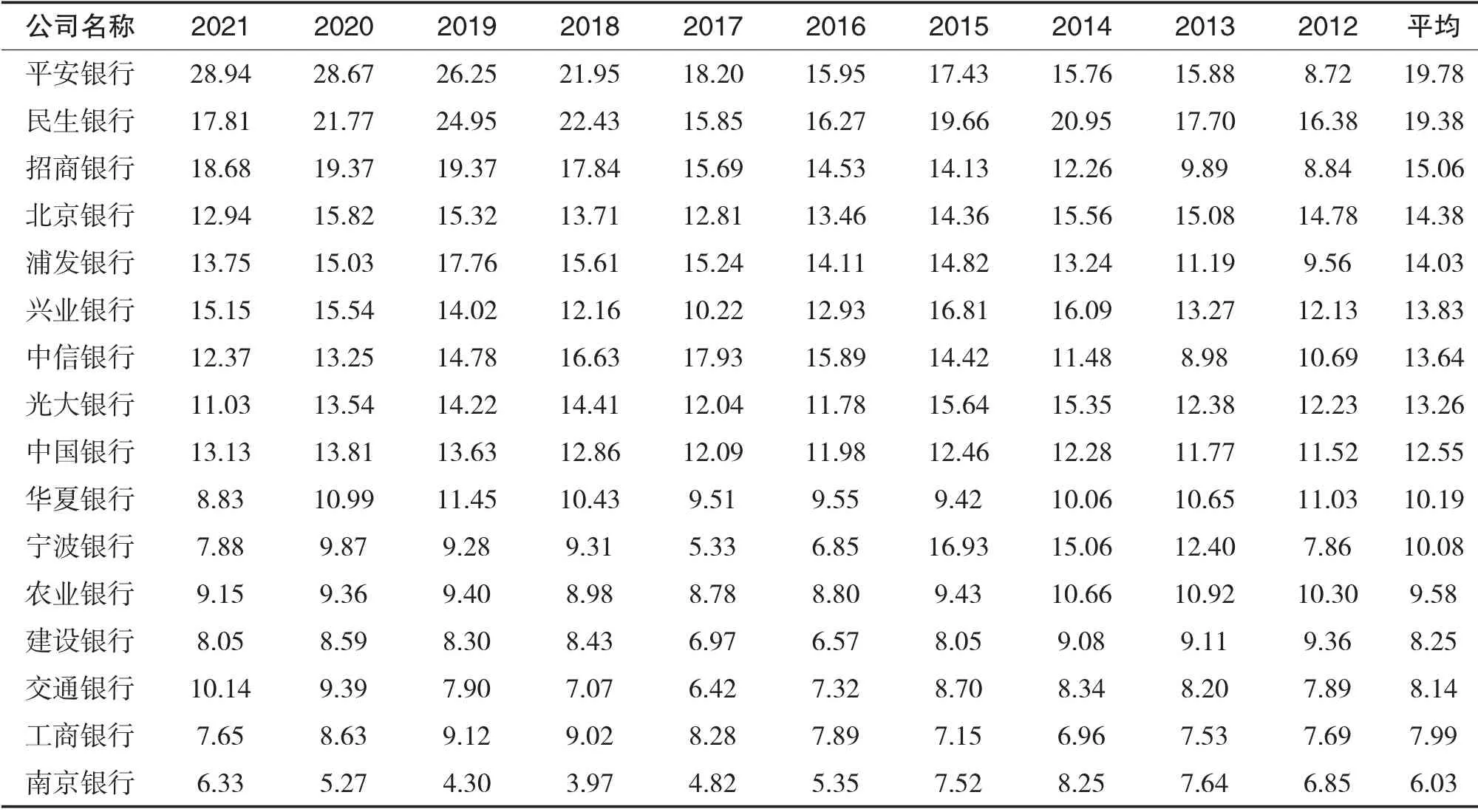
表2 银行业房地产贷款占比（%）

将聚类结果和相关系数结果做进一步对比发现。首先，银行间的相关性都较高，2 簇聚类的结果显示了银行和房地产企业各自的聚集效应，银行基本都聚在一起，但是也有特例，比如兴业银行。其次，相关系数显示，房地产企业两两相关性较低，但是通过聚类可以发现房地产具有波动聚集性。最后，相关性显示头部房地产企业关联性较高，聚类同样证实了这一点。这些都说明，DTW 聚类能更有效地发现波动的聚集性。

综上，银行和房地产企业股价波动具有明显的聚集效应。行业层面上，银行和房地产具有鲜明的行业聚集特点，行业的聚集效应明显。个体层面上，由于房地产企业或银行的经营策略不同，具有特有的聚集效应，相同策略的企业或银行往往会聚在一起，不同策略时则有显著差异。

四、结论与建议

本文探究了将DTW-K-Means 模型应用于金融时间序列进行聚类的理论基础与实际应用，并得到以下结论：

1．利用DTW-K-Means 对16 家上市商业银行和9 家大型房地产上市公司股价波动进行聚类，充分考虑了银行-房地产上市公司股票价格波动的关联性。

2．波动是风险的显性反馈，已实现波动率可以充分发挥高频数据的优势，能够更加精准反映相关信息。DTW-K-Means 聚类结果显示，聚类可以发现行业层面的聚集效应，同行业企业的波动有更高的相似性，更易聚在一起。聚类亦可发现个体企业波动的异质性，只有具有同样波动特征的银行或房地产企业才会聚到一起，说明这些企业往往采用了类似的风险策略、持有类似资产或者具有广泛的业务联系。基于以上结论，本文提出以下建议：

1．投资者在进行投资时，除了关注股票价格的走势，还需重点关注代表风险的波动率指标；构建投资组合时，应考虑风险对冲效应；进行股价预测时，可以寻找波动类似的股票作为外在影响因素，发现数据背后的规律。

2．需要重点关注房地产业和银行业波动的关联性，避免房地产价格波动的风险蔓延到银行板块，避免产生房地产风险-银行风险-金融风险-经济风险的风险传染渠道。同时也要关注银行业的波动风险是否会蔓延到房地产行业，避免产生银行风险-房地产风险-金融风险-实体经济下滑风险。

3．在制定银行和房地产监管政策时，应当考虑单个企业的风险异质性。房地产业贷款占比是银行和房地产关联的重要影响因素，为了避免风险过渡传染，应要求银行进一步披露房地产业贷款信息，真正落实国家对房地产的调控政策，确保房地产在保障民生中发挥重要作用，同时也要避免房地产行业成为风险传染的源头。