弱左型B半群的半格分解

李春华，方洁莹，孟令香，徐保根

(华东交通大学理学院，江西 南昌 330013)

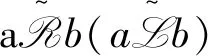
1 预备知识

接下来将介绍本文所需要的定义及相关结论[1-2，15,17-19]。

一般地，记S是半群，E(S)是半群S中幂等元的集合，S1是半群S并上恒等元1的半群。半群S上格林关系L*关系定义如下：令a,b∈S，(a,b)∈L*，当且仅当a,b在S的某个扩半群上具有L关系。相应的，可以定义R*关系。下面以引理的形式给出广义格林关系L*和R*的等价定义。

引理1.1[1]令S为半群且a,b∈S，则下列各款等价：

(1)aL*b[aR*b]

(2)(∀x,y∈S1)ax=ay⟺bx=by[(∀x,y∈S1)xa=ya⟺xb=yb]。

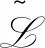
引理1.2[2]令S是半群且a,b∈S，则下列各款等价：

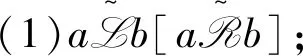
(2)(∀e∈E(S))a=ae⟺b=be[(∀e∈E(S))a=ea⟺b=eb]。

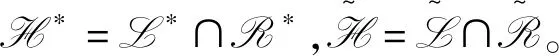
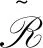
定义1.2[1]令S是任意半群，则称S为左型B半群，若下列条件成立：

(B1)S中幂等元可交换；

(B2)S中每个R*类都含且仅含唯一的幂等元；

(B3)对任意e,f∈E(S1)，a∈S，(aef)+=(ae)+(af)+；

(B4)对任意a∈S，e∈E(S)，若e≤a+，则存在f∈E(S1)使e=(af)+。

定义1.3[15]令S是任意半群，则称S为弱左型B半群，若下列条件成立：

(WB1)S中幂等元可交换；

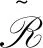
(WB3)对任意e,f∈E(S1)，a∈S，(aef)+=(ae)+(af)+；

(WB4)对任意a∈S，e∈E(S)，若e≤a+，则存在f∈E(S1)使e=(af)+;

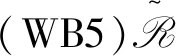
定义1.4[15]若S是任意半群，则称S为(弱)型B半群，若S既为(弱)左型B半群又为(弱)右型B半群。

显然，左型B半群及弱左型B半群均是一元半群(带有一元运算a→a+的半群)，记作(S+，)。

定义1.5令S是弱左型B半群，有如下定义：

N(S)={a∈S|aR*a+}

称I(S)为S的核。

I(S)={a∈S|aRa+}

称N(S)为S的逆元部分。

SαSβ⊆Sαβ

此时，称S是幂单幺半群的半格，记S=(Y,Sα)。

定义1.7[19]假设幂单幺半群Sα，其中α∈Y，Y是指标集且为半格，并且对任意α,β∈Y，若α≥β，则存在同态Sα→Sβ使得

(1)(∀α∈Y)χα,α=1Sα；

(2)对任意α,β,γ∈Y，

若α≥β≥γ，则

S=∪α∈γSαχα,βχβ,γ=χα,γ

在S上可以定义乘法如下：对任意x∈Sα，y∈Sβ，有

xy=(xχα,αβ)(yχβ,αβ)

易证，若x∈Sα，y∈Sβ，z∈Sγ，则(xy)z=(xχα,αβγ)(yχβ,αβγ)(zχγ,αβγ)=x(yz)。因此，该乘法是结合的。由此可知，S是幂单幺半群的强半格，记作

S=S[Y;Sα;χα,β]

定义1.8[19]若f：X→Y和g:Y→X满足以下条件：

(1)f。g=tY；

(2)g。f:X→X是幂等的；

则称f是g的收缩映射。

引理1.3令S是左半适当半群，则(S+,)是一元半群，且下列结论成立：

(A1)a=a2⟹a=a+；

(A2)a+=(a+)+；

(A3)a+b+=b+a+；

(A4)a=a+a；

(A5)(ab)+=a+(ab)+；

(A6)(ab)+=(ab+)+。

证明由左半适当半群的定义可直接推得。

2 弱左型B半群

引理2.1一元半群(S+,)是弱左型B半群当且仅当条件(A1)-(A6)和条件(B3)、(B4)成立。

证明必要性：显然成立。

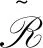
(ce)+ca=(ce)+cea=cea=ca

(ce)+cb=(ce)+ceb=ceb=cb

即有一相同得左恒等元。现证ca与cb有相同得左恒等元集。为此，令f∈E(S)，且有kca=ca，则(fca)+=(ca)+。由(A6)有(fca+)+=(ca+)+，注意a+=b+。于是，(fcb+)+=(cb+)+，进而(fcb)+=(cb)+，因此，

fcb=(fcb)+fcb=(fcb)+fc+cb=

(fcb+)(fc)+cb=(fcb+)(fc·1)+cb=

(fcb+·1)+cb=(fcb)+cb=(cb)+cb=cb

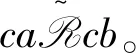
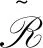
证明由引理2.1可直接推得。

定理2.3令S是弱左型B半群，则下列各款成立：

(1)N(s)={a∈S|x,y∈Sa+,xa=ya⟹x=y}是S的最大左型B一元子半群，

(2)I(S)={a∈S|a是正则元}是S最大逆一元子半群。

证明(1)首先，记A={a∈S：x,y∈Sa+,xa=ya⟹x=y}。令a∈N(s)，x,y∈Sa+并且xa=ya。由aR*a+可知xa+=ya+。

已知x,y∈Sa+，故x=xa+=ya+=y。因此，N(S)⊆A。

下证A⊆N(S)。首先令任意a∈A，x,y∈S使得xa=ya，则由(A3)可知xa+a=ya+a，其中xa+,ya+∈Sa+。故xa+=ya+，由引理1.1，aR*a+，即A⊆N(S)。综上，A=N(S)成立。

令a,b∈N(s)，由N(S)的定义可知aR*a+且满足bR*b+，由于R*是左同余，则有abR*ab+，已知S是弱左型B半群，故(ab)+=(ab+)+，即abR*(ab)+，于是ab∈N(S)。故N(S)是S的子半群。由于S上的一元运算限制在N(S)上是保持不变的，故N(S)是S上的一元子半群。根据左型B半群的定义可知N(S)是左型B半群，注意到N(S)的定义可知N(S)是S中最大的左型B一元子半群。

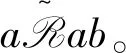
ab=a(xa)(by)b=a(by)(xa)b=(ab)yx(ab)

即ab∈I(S)，所以I(S)是封闭的。S上的一元运算限制在I(S)上是保持一致的，所以I(S)是S上的一元子半群。注意到I(S)中包含了S中所有的正则元，所以I(S)是S的最大逆一元子半群。

推论2.4令S是弱左型B半群，则下列各款成立：

(1)N(S)=S；

(2)S是左型B半群；

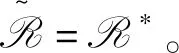
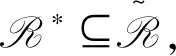
推论2.5令S是弱左型B半群，则下列各款成立：

(1)I(S)=S；

(2)S是逆半群；

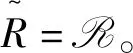
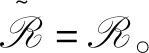
定理2.6令S是弱左型B半群，则下列各款等价：

(1)S是幂单半群的半格；

(2)映射a→a+(a∈S)(1)是S到E(S)的收缩映射，即Sφ=E(S)；

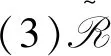
(4)S满足(ab)+=(a+b)+；

(5)S满足(ab)+=a+b+。

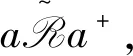
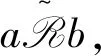
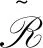
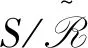
(4)⟹(5)由题设及(A4)可知，

(ab)+=(ab+)+=(a+b+)+=a+b+

故5)成立。

(ac)+=a+c+=b+c+=(bc)+

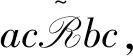
3 弱左型B半群的半格分解

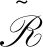
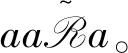
引理3.2令S=(Y;Sα)，其中Y是半格，对任意α∈Y，Sα是幂单幺半群，则S是半群Sα的强半格Y。

证明对任意α∈Y，令eα是Sα中的恒等元。令α≥β，按如下建立映射，

χα,β:a→aeβ(a∈Sα)

则χα,β:Sα→Sβ。由于α≥β并且a,b∈Sα，

(aχα,β)(bχα,β)=(aeβ)(beβ)=

aeβ(beβ)=abeβ=(ab)χα,β

对于α≥β≥γ，有

eβeγ=eγeβeγ=eγeβ=(eγeβ)2=eγ

由于Sγ是幂单的，故对任意a∈Sα，

aχα,βχβ,γ=aeβeγ=aeγ=aχα,γ

一般地，χα,α是Sα上的恒等映射。因此S=[Y;Sα,χα,β]。

以下是本文的主要结论。

定理3.3令S是弱左型B一元半群，则下列各款等价：

(1)S满足a=aa+及(ab)+=(ab)+b+；

(2)S满足ab+=b+a；

(3)S是幂单幺半群的半格；

(4)S是幂单幺半群的强半格。

证明(1)⟹(2)由题设及(A3)、(A4)可得

ab+=(ab+)+ab+=(ab+)+(b+)+ab+=

(ab+)+b+ab+=b+(ab+)+ab+=b+ab+

类似地，

b+a=b+a(b+a)+

(因S满足a=aa+)=(b+a)(b+a+)+=b+ab+a+

(因(A6)及(A2))

=b+aa+b+=b+ab+(因(A4))

(因S满足a=aa+)

故ab+=b+a，因此(2)成立。

(2)⟹(3)首先，由(A4)、(A6)及题设可知

(ab)+=(ab+)+=(b+a)+=(b+a+)+=b+a+=a+b+

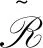
(3)⟹(4)由引理4.2易得。

(4)⟹(1)令S=[Y;Sα,χα,β]，对任意α∈Y，Sα是幂单幺半群，包含恒等元eα。假设对任意a∈Sα，α∈Y，有a+=eα。显然，由S是弱左型B半群，定理得余下证明可由定理3.6直接推得。