核心素养下数学猜想在数学教学中的应用

◎商钰莹 （张家港市合兴初级中学，江苏 张家港 215600）

教育是培养人的事业，教师是教育的主力军，教学具有教育性，数学课堂教学不仅仅是计算和证明，还可以进行核心素养的渗透、思维能力的培养、解题方法的总结．随着我国新课改的不断推进，教学对学生核心素养的要求也越来越高．核心素养理念是培养学生思维能力的重要手段，数学教学改革要求数学教师站在核心素养的高度，将学生数学猜想能力的培养贯穿于数学教学中，由此引导学生数学核心素养的逐步养成和数学思维的增强．数学猜想是数学发展的重要路径，在教育快速发展的今天，每一个数学理论和分支的产生和发展都烙上了数学猜想的烙印．数学猜想对一些数学理论的证明有着重要的意义．

一、数学猜想的定义及其特征

数学猜想以数学知识和数学事实为基础．数学猜想如果被验证真实存在，就会转化为数学定理，成为数学理论体系的重要组成部分，数学猜想不仅有利于数学理论的发展，还有利于数学方法论的研究．

逻辑和非逻辑两部分构成数学猜想，所以教学猜想是科学的，人们通过推理和论证过程，确定猜想的正确性．推理和论证过程则是一种创造性的思维活动，有利于发展学生的思维能力．

二、核心素养下数学猜想的指导作用

核心素养背景下，教师应引导学生学会构建数学知识体系，为学生设计符合他们认知水平的学习过程．教师要懂猜想、会猜想，才能培养出具有猜想能力的学生，教师应在教学过程中注重学生数学思维、解题方法的培养．

要使学生掌握解题方法，教师就必须引导学生“再创造”．数学家已经对知识进行了论证和研究，学生要想发现规律，需要教师的指点和帮助．一般来说，猜想是新旧知识的融合，学生通过归纳、类比、观察、联想，得到最终的论证结果．

三、数学教学中的数学猜想

（一）归纳猜想

归纳猜想是解决数学问题的重要思维方法，归纳猜想就是按照一类事物的部分对象具备的某种性质，通过对问题的观察、分析和讨论，发现其内部具有的某种共性或规律，从而推出这类事物的一切对象都具有这种性质的一种推理．归纳猜想是从特殊到一般的过程．

例如，52＋122＝132，72＋242＝252，92＋402＝412，求第n个式子．

5、7、9 是连续的奇数，则猜想第n个式子中的第一位是2n＋1．12、13，24、25，40、41 是连续的两个自然数，则设第二、三个数是分别k，k＋1．根据（2n＋1）2＋k2＝（k＋1）2，可得k＝2n2＋2n，所以第n个式子是（2n＋1）2＋（2n2＋2n）2＝（2n2＋2n＋1）2．

又如，算式2（3＋1）×（32＋1）×（34＋1）× …×（316＋1）＋1，求其个位数字．

此题主要考查了利用平方差公式探究规律．根据题中式子的特点，我们可以将2 写成3-1，进行式子的简化计算，得到：原式＝332，再根据3 的幂的特点，找出个位数字的规律，即可求值．原式＝（3-1）（3＋1）×（32＋1）×（34＋1）×…×（316＋1）＋1＝（32-1）×（32＋1）×（34＋1）×…×（316＋1）＋1＝（34-1）×（34＋1）×…×（316＋1）＋1＝332-1＋1＝332．

由31＝3，32＝9，33＝27，34＝81，35＝243，…，得到个位数是3、9、7、1 的循环，32÷4＝8，所以332的个位数是1．

近年来，越来越多的创新探究题出现在中考压轴题中，通常涉及对图形变化的归纳，对几何图形中数量关系的猜测探究，对位置关系及几何形状的猜测，这些都需要我们用心探索，掌握技巧．

如图1，在△ABC中，∠A＝x°，A1是∠ABC与∠ACD的角平分线交点，A2是∠A1BC与∠A1CD的角平分线交点，A2022是∠A2021BC与∠A2021CD的角平分线交点，求∠A2022．

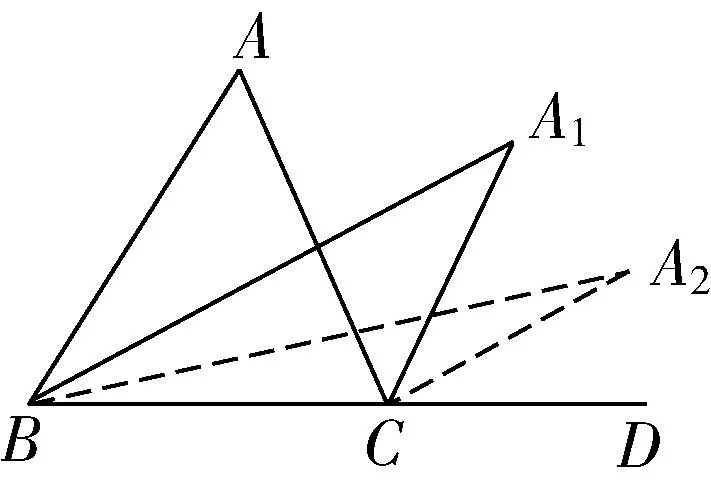
图1

找出∠A1和∠A之间的规律是解题的关键．找出规律即可求出∠A2022．

因为BA1平分∠ABC，A1C平分∠ACD，所以∠A1CD＝

（二）类比猜想

类比是一种主观的、不充分的、似是而非的推理，所以，为了证实猜想的有效性，我们要经过严密的逻辑论证．

学生在学习立体几何时，可以类比平面几何中的结论．如图2，长方形与长方体类比，类比关系如下：

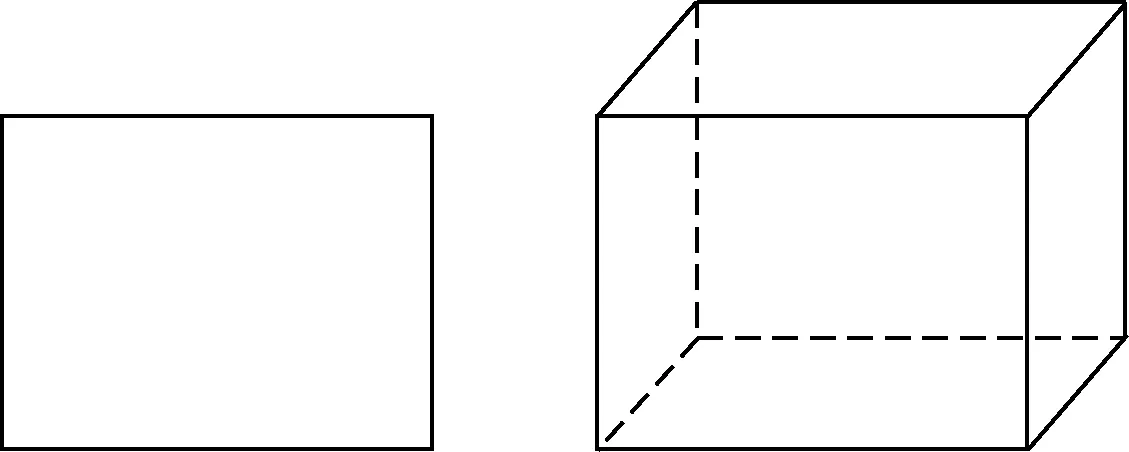
图2

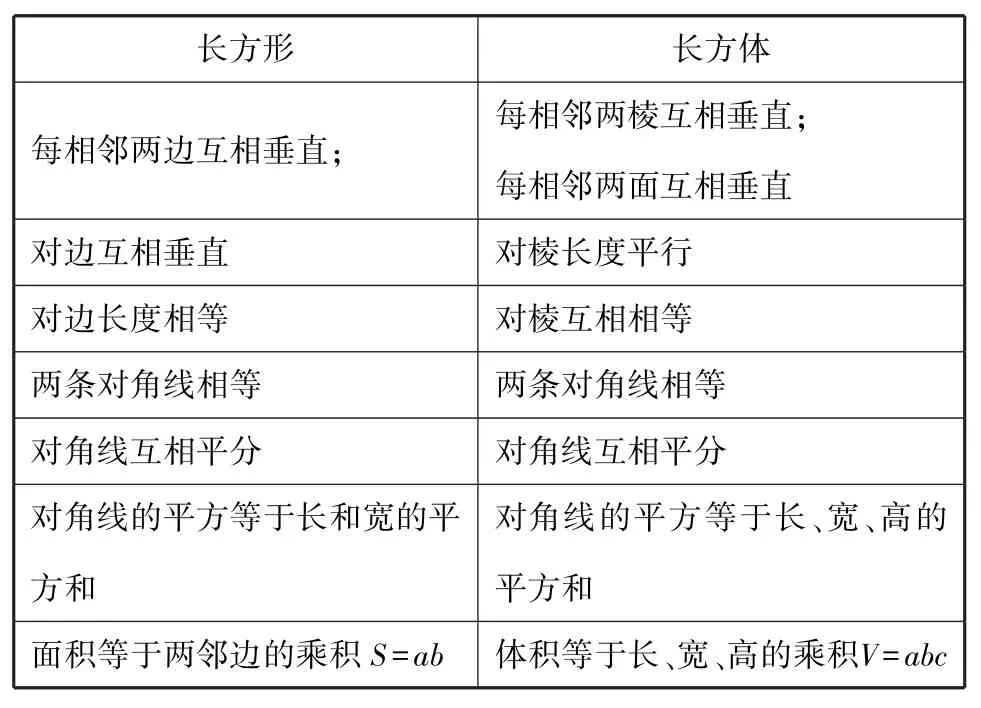
长方形长方体每相邻两边互相垂直；每相邻两棱互相垂直；每相邻两面互相垂直对边互相垂直对棱长度平行对边长度相等对棱互相相等两条对角线相等两条对角线相等对角线互相平分对角线互相平分对角线的平方等于长和宽的平方和对角线的平方等于长、宽、高的平方和面积等于两邻边的乘积S＝ab体积等于长、宽、高的乘积V＝abc

在学习相似三角形的性质时，可以类比全等三角形（如图3）．类比关系如下表：

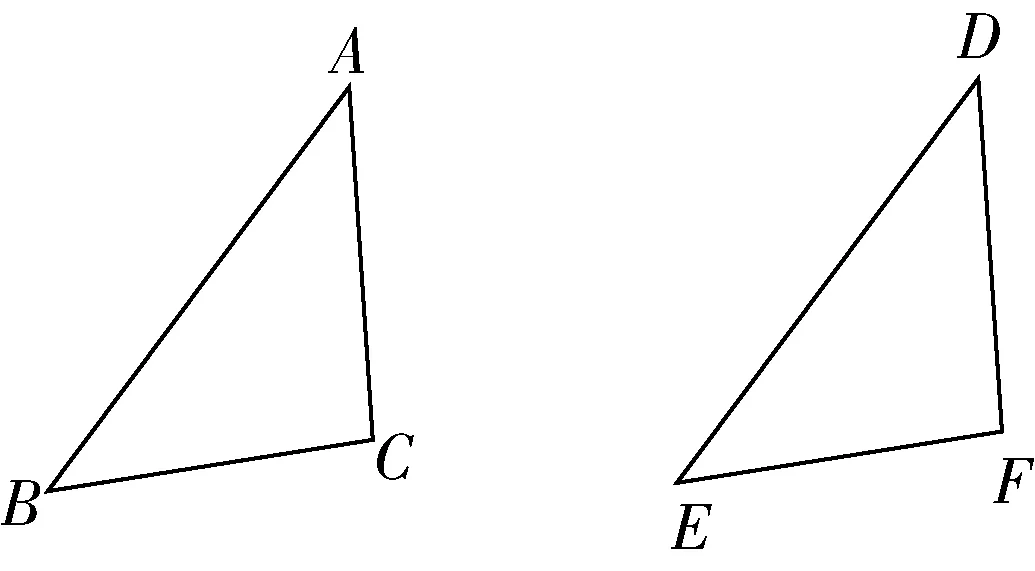
图3

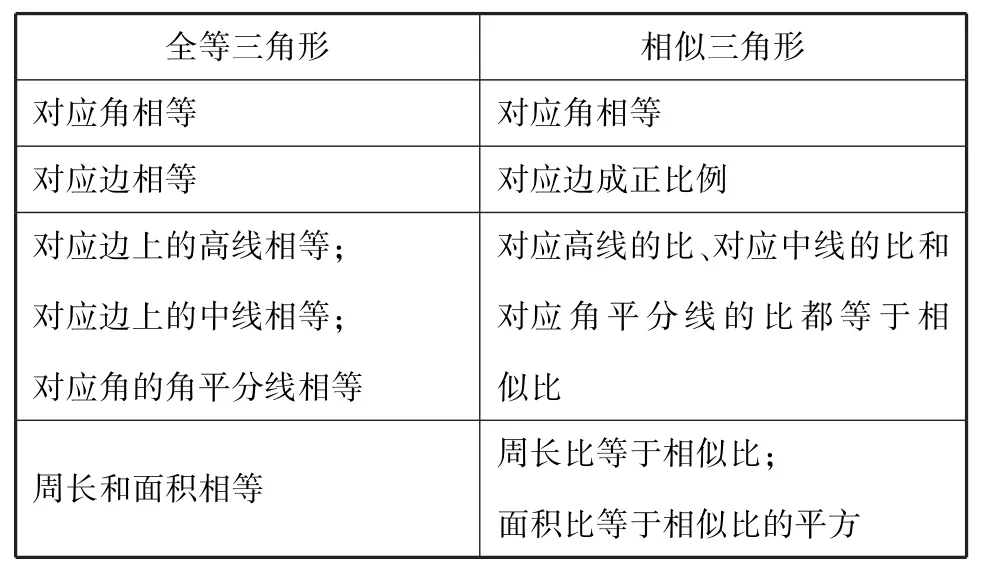
全等三角形相似三角形对应角相等对应角相等对应边相等对应边成正比例对应边上的高线相等；对应边上的中线相等；对应角的角平分线相等对应高线的比、对应中线的比和对应角平分线的比都等于相似比周长和面积相等周长比等于相似比；面积比等于相似比的平方

在求一元n次方程的根与系数之间的关系时，设ax2＋bx＋c＝0 的两个根分别是x1，x2，则有ax2＋bx＋c＝a（x-x1）·（x-x2），整理得类比此方法，我们可以求出一元n次方程根与系数的关系．

设n次多项式f（x）＝anxn＋an-1xn-1＋…＋a1x＋a0的n个根为x1，x2，…，xn，则有anxn＋an-1xn-1＋…＋a1x＋a0＝an（xx1）·（x-x2）…（x-xn），整理得：

（三）观察猜想

观察猜想就是指导学生观察和分析数学命题的结构、解题的过程，从而提出新的结论或论点．观察猜想是发现问题和解决问题的重要途径．中学生的抽象思维较弱，在几何图形教学过程中，学生可以通过观察图形的变换、转化、运动、应用等过程，提升空间几何感．

例如，41＝4，42＝16，43＝64，44＝256，45＝1024，46＝4096，…观察等式，写出4101的末位数字．

我们观察以上等式，可以发现等式右边数的末位数是4、6 这2 个数字的循环，由于101÷4＝25…1，所以4101的末位数字是4．

此题考查用代数式表示数量．我们仔细观察分子和分母，易发现分子是从1 开始的奇数，分母是从3 开始的奇数．因此，第n个数应为形如2n-1 或2n＋1（n为正整数）的式子表示奇数．一般地，对于一个有规律排列的数列，当你探索出其中的规律并用含n的式子表示出第n个数之后，可以列举数值代入表达式来证明猜想正确．

再如，若“！”是一种数学运算符号，并且：1！＝1，2！＝2×1＝2，3！＝3×2×1＝6，4！＝4×3×2×1＝24，…求的值．

新定义题型是近年来的热点问题，学生要读懂题目，观察其规律．因为100！＝100×99×98×97×…×1，98！＝98×97×…× 1，所以＝ 100 ×99＝9900．

在学习用配方法解一元二次方程时，观察下列各式中常数与一次项系数之间的关系．

（1）x2＋6x＋32＝（x＋3）2；

（2）x2＋8x＋42＝（x＋4）2；

（3）x2-4x＋22＝（x-2）2；

（4）x2＋px＋（ ）2＝（x＋）2．

我们观察等式的左边，可以发现所填的常数是一次项系数一半的平方，通过观察猜想，总结出一般规律x2＋px＋进而归纳出配方法的步骤．

（四）联想猜想

联想是类比的发展．教学过程中，我们通过联想，可以将新旧知识串联起来，有利于知识的发展与迁移，提高数学思维的灵敏性，从而完善学生的知识结构．

例如，学生学习了平行四边形的性质后，可以通过联想得到长方形、菱形和正方形的性质．在求不规则石块的体积时，根据曹冲称象的故事，我们可以利用规则的容器，求出水的体积，得出所求石块的体积．

又如，已知tanα＝2，求sin2α-sinαcosα＋2 的值．

若根据tanα＝2 直接求正、余弦的值，则会出现取正负值的问题．我们应利用tanα＝2，求出的解，在式子中构造tanα．在解题时学生应注意式子中的分母问题，联想到具有特殊性的式子sin2α＋cos2α＝1，即sin2α-

四、核心素养下数学猜想在数学教学中的意义

课堂是教学的主阵地，课堂教学是落实对学生核心素养培养的关键途径．在中学数学教学中，教师需要为学生营造良好的课堂氛围和学习环境，根据班级学生情况，因人施教，把学生放在课堂的主体位置，关注学生在课堂中的每一个眼神、每一个动作、每一次发言，以培养学生的数学核心素养为目标，结合现代教育理论，积极联系学生的生活经验和认知水平，探索并实践培养学生猜想能力的有效途径，帮助学生形成良好的数学学习思维，从而提升数学课堂的学习效率，促进学生的全面发展．

猜想对数学理论的建立和发展有着重要的作用．猜想是学生对知识信息进行构建的一种数学思维活动，具有一定的科学性和预测性．猜想过程不再是枯燥的填鸭式教学，通过让学生先猜结果，再验证是否正确，激发学生学习数学的兴趣．长期进行猜想训练，有利于提高学生的学习效率，从而促进学生核心素养的发展．在教学过程中，教师要注重培养学生的数学猜想能力，通过教师的引导，让课堂教学更加符合学生的认知规律，从而落实对学生核心素养的培养目标．