配电网接地故障下相电流暂态变化量的分析及应用
朱秀香,刘肖骢,姚敏东,崔彦波,刘克显
(1. 南瑞集团有限公司(国网电力科学研究院有限公司),江苏省南京市 211106;2. 北京科东电力控制系统有限责任公司,北京市 100192;3. 国网黑龙江省电力有限公司,黑龙江省哈尔滨市 150090)
0 引言
随着智能配电网的发展,在提升供电可靠性的同时,还应重视人身安全、减少电气火灾。小电流接地系统带故障长时间运行,除了可能引发相间短路故障、电缆沟着火等,还可能导致人身触电与火灾事故[1-3]。《配电网技术导则》[4]中规定,在躲过瞬时性接地故障后,要快速就近隔离故障。同时,分布式电源(DG)的大量部署改变了配电网的馈线结构,发生故障后如不能及时隔离DG,可能带来二次故障引发停电等事故。因此,对单相接地故障的快速诊断提出了更高要求[5-7]。
目前,小电流接地故障选线定位技术已有大量研究。文献[8]提出利用神经网络融合多个特征量提高接地故障识别准确率,具有容错性高的优点,但训练后的模型依赖于历史训练库和准确性。文献[9-11]提出利用区段两侧零序电流的差异性或线路两端的故障暂态波形确定故障区段,由于要比较不同检测点暂态电流信号,需要精确的时钟同步及可靠的通信条件。文献[12]提出利用暂态无功功率的方向确定故障区段,通过测量架空线路下方垂直地面方向电场获取暂态电压信息。但电场的测量容易受安装高度、环境等因素的影响。文献[13]提出在特征频带内利用故障相与健全相电流故障分量比值大小进行选线,该方法具有自具性,可实现故障的就地判别,但未给出故障定位方案。文献[14-15]提出在特征频带内利用相电流与相电压突变量的导数相关性判断线路状态,但需要测量电压信号,用于配电线路时有限制。文献[16]分析了故障点上游健全相、故障相暂态电流分量与暂态零模电流的关系,提出利用故障暂态电流分量的方向确定故障点位置,但未对故障点下游相暂态电流分量与暂态零模电流关系进行详细分析。
已有针对单相接地故障暂态特性的分析主要集中在暂态零模特性及其分布规律方面,对暂态相分量的分析证明相对较少。本文分析了单相接地故障后相电流变化量的稳态及暂态特性,建立了包含故障点上游、下游线路的复合模网等效电路。分别对故障区段(故障点至母线段)、健全区段(非故障线路、故障点下游)故障相和健全相暂态电流变化量的幅值及方向进行了理论分析,计算了故障相与健全相有效值的比值。在此基础上,利用相暂态电流变化量的比值及方向,提出了一种故障定位的新方法,可实现接地故障的就地判别。PSCAD 仿真及现场试验数据验证了多种故障情况下所提算法的有效性。
1 单相接地故障相电流变化量特征分析
1.1 基于相电流变化量的稳态分析
故障线路J在故障点之前对应故障相电流的变化量[17]ΔİJP为:

式 中:Z0J=1/(jωCJ),其 中CJ为 线 路J每 相 对 地 电容;U̇P为故障前的P相电压(P=A,B,C);U̇'P为故障后的P相电压;U̇0为故障前后的相电压突变量;İf为故障点的接地电流,方向由线路指向大地。
故障区段健全相及健全区段对应相电流的变化量ΔİKP为:
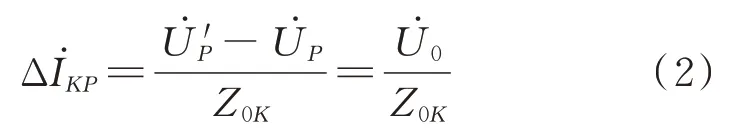
式中:Z0K=1/(jωCK),其中,CK为线路K每相对地电容。
由式(1)、式(2)可知,健全区段产生的相电流变化量均为相电压突变量作用于线路对地电容的电流,其三相电流变化量的波形相似。但故障区段故障相电流变化量还包括了接地点电流,三相电流变化量波形不一致。通过以上分析,利用健全区段三相电流变化量波形一致、故障区段三相电流变化量波形差异大的特点,可进行故障选线及区段定位。
但谐振接地系统通常采用过补偿方式,由于消弧线圈电感电流补偿了总的接地电容电流,使İf显著减小为残余电流,且故障线路故障相电流变化量的方向与健全相相同,存在故障区段故障相与健全相电流变化量波形差异较小的情况。同时,在间歇性电弧接地故障中较难捕捉稳态信号。只利用三相电流稳态变化量进行故障定位易出现动作死区。
1.2 基于相电流变化量的暂态分析
1.2.1 谐振接地系统暂态特性分析
对于三相系统,由于各相线路间存在电磁耦合,利用Karenbauer 转换为没有耦合的模量系统。故障暂态特性的计算只考虑故障附加分量,在谐振接地系统中,根据故障点边界条件建立基于分布参数的故障分量复合模网结构,如图1 所示。0、1、2 模阻抗分别由故障点上游和下游的模阻抗并联而成。由于接地故障的暂态频率较高,变压器、负荷等设备可采用集中参数模型,线路采用∏型分布参数模型,uf为故障点虚拟电源,其数值为故障前故障相的电压值;Rg为接地点的过渡电阻;L0(L1、L2)、R0(R1、R2)、C0(C1、C2)分别为单位长度线路等效的零模(线模)电感、零模(线模)电阻及零模(线模)电容;Ls1(Rs1)、Ls2(Rs2)为变压器线模电感(电阻);LK为消弧线圈等 效 电 感;Zd11(Zd12),Zd21(Zd22),…,Zdn1(Zdn2)和ZdJ1(ZdJ2)分别为健全线路1,2,…,n及故障线路J的负荷线模阻抗。
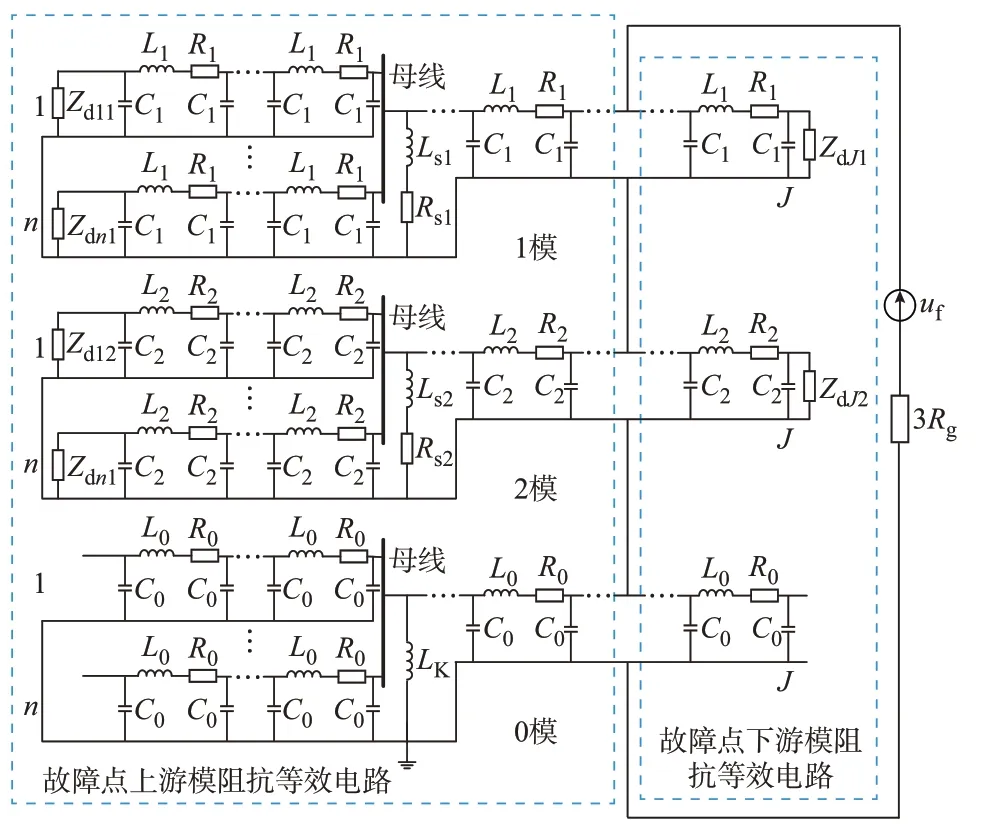
图1 基于分布参数的故障分量复合模网结构图Fig.1 Structure diagram of fault-component-compositemode network based on distributed parameters
由图1 可以看出,故障点上游的1 模阻抗为健全线路的线模阻抗与变压器并联后再与故障点到母线线模阻抗串联;故障点下游1 模阻抗等效为故障点到末端线路的线模阻抗与负荷线模阻抗串联;线模等效电路如图2(a)所示,考虑变压器的线模阻抗远小于线路分布电容容抗,图中忽略了线模分布电容的影响。图2 中,ZL11(i11),ZL21(i12),…,ZLn1(i1n)为健全线路1,2,…,n的线模阻抗(电流);Zfb1(Zfa1)为故障点至母线段(线路末端)的线模阻抗;if1b(if1a)为故障点前(后)的线模电流,Zs1=Rs1+jωLs1为变压器的线模阻抗;u1f为虚拟电源的线模分量。
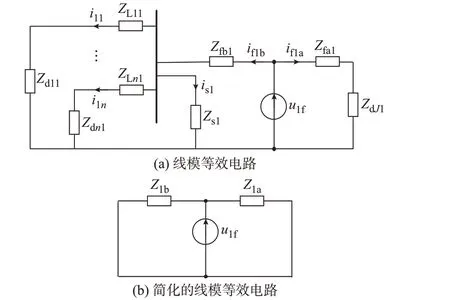
图2 线模网络等效电路Fig.2 Equivalent circuit of line-mode network
根据图2(a)的线模等效电路可知,故障点上游的1 模阻抗为:
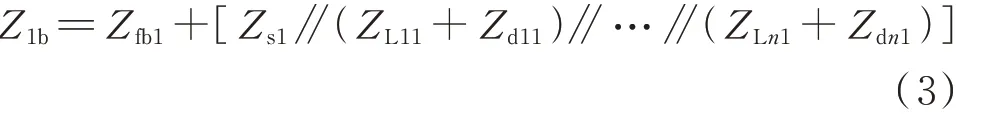
故障点下游的1 模阻抗为:

简化后的线模等效电路如图2(b)所示。其中,故障点上、下游的2 模阻抗Z2b、Z2a分别满足Z1b=Z2b,Z1a=Z2a。
由图1 可以看出,谐振接地系统中,故障点上游的零模阻抗由各非故障线路零模阻抗与消弧线圈阻抗相互并联后再与故障点至母线段零模阻抗串联;故障点下游零模阻抗只有故障点到末端线路的零模阻抗。根据文献[18]提出的模型简化原则,可将各线路的分布参数模型简化为∏型集中参数模型,如图3(a)所示,再将故障点上游的集中参数模型合并为∏模型,最后分别将故障点上、下游等效的∏模型简化为Γ 模型,如图3(b)所示。
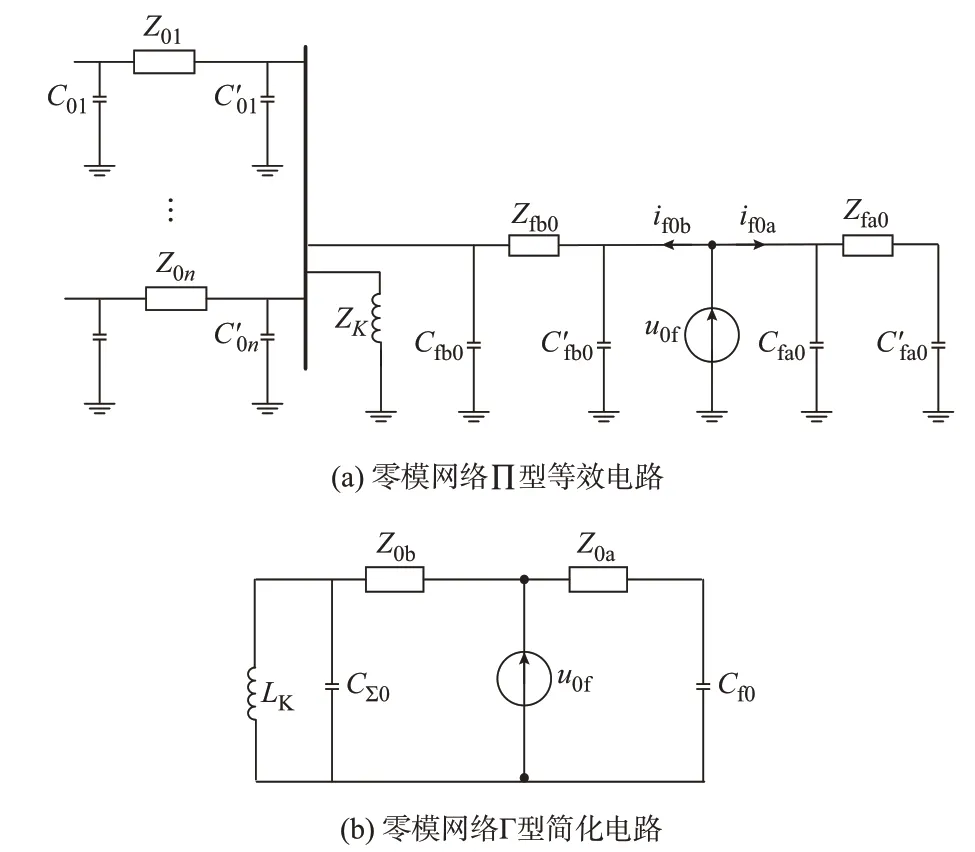
图3 零模网络等效电路Fig.3 Equivalent circuit of zero-mode network
在图3(a)中,u0f为虚拟电源的零模分量;Zfb0(Zfa0)、Cfb0(Cfa0)、C'fb0(C'fa0)分别为故障点至母线段(线路末端)∏型集中参数模型的等效阻抗及两侧电容;长度为lk的第k条健全线路的∏型集中参数模型的阻抗Z0k=R0k+jωL0k,k=1,2,…,n,其中,R0k≈0.500 5R0lk,L0k≈0.500 5L0lk,两 侧 的 电 容 为C0k≈0.189 4C0lk,C'0k≈0.810 6C0lk。


通过对线模和零模等效电路的分析,可以得出故障分量复合模网等效电路如图4(a)所示,图4(a)可进一步等效为图4(b)。图中,i0为系统零模电流。由 于 线 模1、2 的 阻 抗Z1、Z2相 同,总 的 线 模 阻 抗2Z1=2(Z1b//Z1a)。
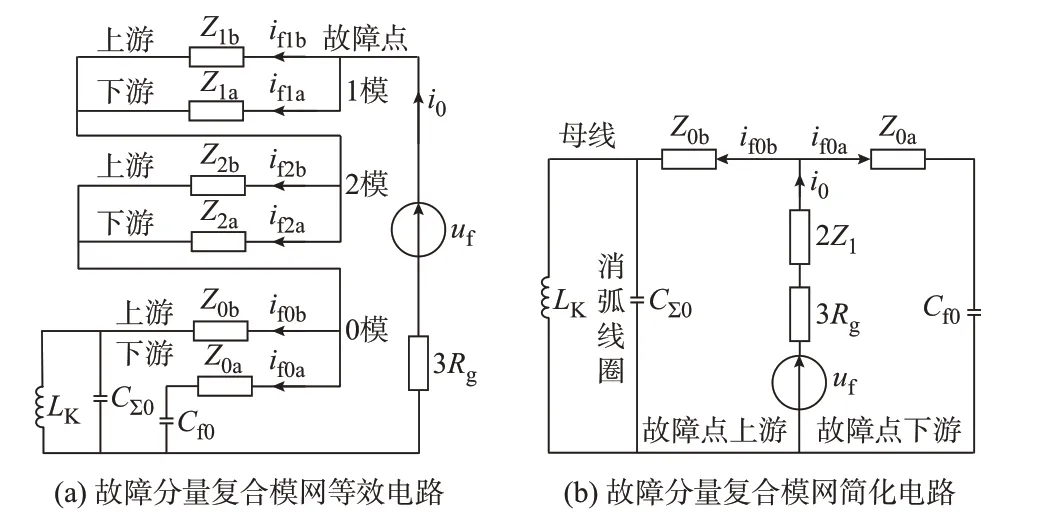
图4 接地故障暂态等值电路Fig.4 Transient equivalent circuit of grounding fault
1.2.2 中性点不接地系统暂态特性分析
中性点不接地系统的线模网络等效电路与谐振接地系统相同,不再赘述。中性点不接地系统零模等效电路未涉及图3 中消弧线圈的感抗,其余相关线路参数的计算与谐振接地系统相同。
1.3 故障点上游相暂态电流变化量分析
1.3.1 故障点至母线段相暂态电流变化量分析
根据图4 所示等效电路可知,从故障点到母线段的暂态故障电流包含了0、1、2 模的暂态分量。因此,故障相暂态电流变化量ΔiJA的表达式为:
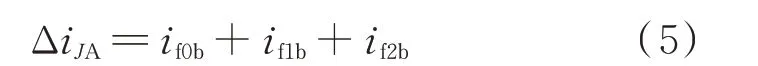
其方向由故障点流向母线。
由于变压器的线模阻抗Zs1相对于健全线路与负荷线模阻抗之和较小,满足Zs1≪ZLk1+Zdk1,忽略健全线路线模阻抗,故障点上游线模阻抗的表达式(3)可简化为:
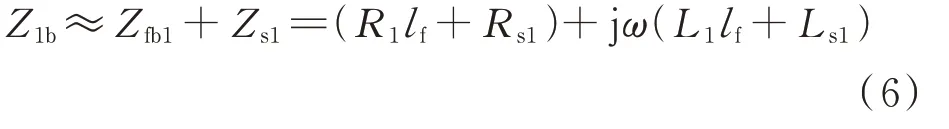
由于负荷的多样性,故障点下游线路的线模阻抗特性不易确定。一般条件下,故障点下游的负荷阻抗远大于故障点上游的线模阻抗,因此可忽略故障点下游的线模阻抗[19-20],即在暂态过程的主谐振频率范围内满足Zfb1+Zs1≪Zfa1+ZdJ1时,图4(a)的线模电流满足if1b=if2b≈i0。因此,式(5)可进一步简化为:
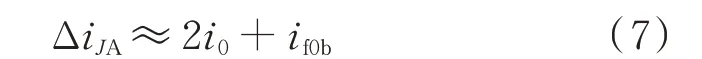
根据上述分析,由Karenbauer 相模变换的关系可知,故障区段健全相暂态电流变化量为:
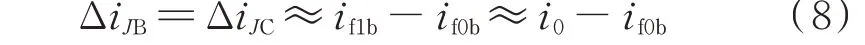
其方向由母线流向故障点。

2)特殊情况下(当配电网仅有一条馈线或故障馈线长度大于其他健全馈线长度之和,且故障点的位置靠近母线时),即CΣ0 通过上述分析可以看出,一般情况下,中性点不接地系统及谐振接地系统均满足故障区段健全相暂态电流变化量波形一致;当CΣ0≥CJ时,故障相与健全相暂态电流变化量的比值大于等于3,当CΣ0 1.3.2 非故障线路相暂态电流变化量的分析 由图2(a)所示等效电路可知,if1b=is1+i11+…+i1n。上文已分析受变压器线模阻抗较小的影响,故障点上游的线模阻抗为Z1b≈Zfb1+Zs1,因此故障点上游线模电流主要流经故障线路至母线段,而非故障线路的线模电流i11,i12,…,i1n相对很小。 由图3(a)所示的等效电路可知,与线模电流不同,非故障线路零模电流不受变压器模阻抗的影响,故障点上游零模电流主要流经故障点至母线段及各非故障线路。因此,一般情况下满足非故障线路的零模电流大于线模电流,在忽略其线模电流的情况下,非故障线路k的三相暂态电流变化量的表达式为: 式中:i0k、i1k、i2k分别为线路k的零模和线模电流。 因此,暂态电流变化量有效值的比值KR≈1。 通过以上分析可知,一般情况下,谐振接地系统和中性点不接地系统均满足非故障线路三相暂态电流的变化量基本相同,故障相与健全相暂态电流变化量有效值的比值约等于1,且三相暂态电流方向相同。 根据图4 等效电路可知,故障点下游故障相暂态电流变化量为: 由Karenbauer 相模变换的关系可知,故障点下游健全相暂态电流变化量为: 故障点下游线路健全相暂态电流变化量相似。由上述分析可知,一般条件下,故障点下游的负荷阻抗远大于故障点上游的线模阻抗,因此故障点下游的线模电流if1a相对较小。通过图4(b)所示等效电路可知[21-22],if0a的大小受故障线路长度、故障位置及接地点过渡电阻等影响。当if0a≈i0时,考虑到线模电流主要流经故障点至母线段,即i0≫if1a,可忽略if1a的影响,故障相与健全相暂态电流变化量有效值的比值KR约为1;当系统零模电流主要流经故障点上游时,if0a较小,不能忽略if1a的影响,其有效值的比值KR不能确定。 通过上述分析可知,在故障点下游仅根据故障相与健全相暂态电流变化量的比值难以确定故障线路故障点位置。由于故障点下游三相暂态电流变化量的方向相同,都是由母线流向线路,而故障区段故障相与健全相暂态电流变化量的方向相反,可利用相暂态电流变化量的方向作为辅助判断。依次计算ΔiJAf、ΔiJBf、ΔiJCf中每两相暂态电流变化量点积积分平均值,利用平均值的正负判断每两相电流方向,有 式中:ρAB为A、B 两相暂态电流变化量方向的判断量;T为积分时间,为故障后一个工频周期。当ρAB为正时,表明被测量信号ΔiJAf、ΔiJBf同向;当ρAB为负时,表明被测量信号ΔiJAf、ΔiJBf反向,同理可计算出ρBC、ρCA的值。若ρAB、ρBC、ρCA中有2 个 小于0、1 个大于0,表示三相暂态电流变化量方向不一致,确定为故障区段,否则确定为健全区段。 1.5.1 负载电流变化的影响 1)低压单相负载变化 当配电变压器采用Dyn11 接线方式,低压侧A相负载变化时,反映到中压侧的电流变化特征为:A、B 两相电流变化量在数值上相等、相位相反,C 相电流变化量为0。 当配电变压器采用Yyn0 接线方式,低压侧A相负载变化时,反映到中压侧的电流变化特征为:A相电流变化量为B、C 相的2 倍,且与B、C 相的相位相反。 2)低压侧三相负载变化 当低压侧的三相负载发生变化时,反映到中压侧的电流特征为[23]:三相电流变化量的大小一致,相位相差120°。 通过上述分析可以看出,低压侧负载电流变化引起的线路电流变化特征区别于故障区段暂态电流变化量的特征,不会引起线路的误判。由于特殊情况下,故障区段故障相与健全相暂态电流变化量的比值大于等于2,当低压单相负载变化且变压器为Yyn0 接线方式时,会对故障区段定位造成一定影响。考虑到负载电流的变化不会影响中压侧的零序电流,特殊情况下可利用零序电流作为故障启动条件之一。 1.5.2 三相参数不平衡的影响 三相参数不平衡是由三相对地电容不平衡等引起的,配电网发生单相接地故障后,有可能导致健全线路三相电流变化量不一致。正常运行时三相电流不平衡度不超过15%。考虑极端情况,假定A 相的 电 流 变 化 量 ΔikA=(1+0.15)ΔikB=(1+0.15)ΔikC。可以算出健全线路k的A 相与B(C)相暂态电流变化量的比值约为1.15,与故障区段的比值(一般情况下该比值大于等于3,特殊情况下大于等于2)相差较大,不会引起健全区段的误判。 基于以上分析,利用相暂态电流变化量的幅值和方向确定故障区段的流程如图5 所示。 图5 故障区段定位流程图Fig.5 Flow chart of fault section location 1)对三相电流进行数据采样并合成零序电流,为了准确捕捉暂态信号,采样频率选为12.8 kHz。配电终端设计时需考虑信号的高速采集、实时存储和CPU 的处理能力等。 2)对于无法获取三相/零序电压的配电终端,根据零序电流/相电流暂态量的变化启动,并保存带有时间标签的故障波形,将故障前一周期电流采样值记忆下来,再与故障后的电流采样值相减得到电流变化量Δif,如式(15)所示。 式中:iφ(ks)为故障后相电流采样值;iφ(ks-N)为故障前相电流采样值。 3)取故障后一周期相暂态电流的变化量,计算每两相暂态电流变化量有效值的比值Kxy,如式(16)所示。 式中:x、y=A,B,C,x≠y,表示取A,B,C 三相;Δix、Δiy分别为x、y相的暂态电流变化量。 4)根据Kxy的值进行接地故障初判。考虑一般情况下满足CΣ0≥CJ,即故障区段故障相与健全相暂态电流变化量的比值大于等于3。根据实际现场的计算误差,取判断阈值Kset1=2.7(当CΣ0 5)对于可能的故障区段,利用特征频带内相暂态电流变化量的方向作为辅助判断。对于一般配电系统工程应用,中性点不接地系统可选0~1 250 Hz,谐振接地系统中可选156.25~1 250 Hz 作为相暂态电流变化量提取的特征频段[24-25]。在特征频段内对应线模网络的阻抗特性呈感性,零模网络健全线路的阻抗特性呈容性,与图4 建立的接地故障暂态等值电路是一致的,因此可按上述特征频段提取相暂态电流变化量进行方向判断。对于特征提取后的数据,根据式(14)依次计算ρAB、ρBC、ρCA的值,若ρAB、ρBC、ρCA中有2 个小于0、1 个大于0,表示三相暂态电流变化量方向不一致确定为故障区段,否则确定为健全区段。 目前,基于暂态信号的小电流接地故障检测方法取得了较为广泛的应用。基于暂态零序电流群体比较的方法适用于变电站选线装置,需要比较所有出线暂态零序电流的幅值和极性。基于暂态接地故障方向的方法适用于线路终端装置,在特征频段内故障线路暂态零模电压的导数与零模电流的乘积为负值,非故障线路为正值。文献[14]基于相电压、相电流突变量特征的故障区段定位方法适用于线路终端装置,在特征频段内故障区段故障相的电流突变量与相电压突变量的导数满足负相关,健全区段满足正相关。 与常用的基于暂态量的故障检测方法(暂态零序电流群体比较法、暂态接地故障方向法、相电压相电流突变量特征法)相比,本文所采用的相暂态电流变化量方法对通信的依赖较低,不需要电压信号及相邻检测点的时间同步,可在配电馈线终端单元(FTU)、故障指示器等设备中实现,可用于电缆分支箱和环网柜中难以获取零序电压或相电压的场合。具体性能对比如表1 所示。 表1 配电线路常用暂态故障检测方法比较Table 1 Comparison of transient fault detection methods for distribution lines 基于PSCAD 搭建一个10 kV 小电流接地系统仿真模型,如图6 所示。系统有4 条主馈线,主馈线L1、L2、L4为 架 空 线,L3为 电 缆 线 路。开 关S 打 开 时为中性点不接地系统,闭合时为消弧线圈接地系统,过补偿度为5%。开关Q 打开时表示系统未接入DG,闭合时表示系统接入DG。其中,DG 的出线电压为690 V,额定容量为1.5 MV·A,并网变压器的容量为2 MV·A,电压变比为0.69/10,接线方式为Dy 型,即并网DG 采用不接地方式。仿真采样频率为12.8 kHz。利用MATLAB 处理采样数据。 图6 仿真系统模型Fig.6 Simulation model of system 谐振接地系统距母线16 km 的L4线路发生接地故障,故障发生在A 相电压峰值时刻,故障后一周期各检测点的暂态电流变化量波形见附录A 图A1,所有监测点均满足健全相波形基本一致。检测点1、2、3 的三相电流波形基本一致,对应检测点在非故障线路上;检测点4 的故障相暂态电流变化量远大于健全相,对应检测点在故障区段上;检测点5、6 故障相的振荡频率与健全相不一致,振荡频率受线路长度的影响,长度越短振荡频率越高,对应检测点在故障点下游。验证了本文分析的故障点至母线段、非故障线路及故障点下游的暂态特性。 在谐振接地系统下分别仿真验证了不同接地过渡电阻、故障发生时刻、故障位置以及接入DG 后基于相暂态电流变化量的故障区段定位算法的有效性。由于各检测点健全相波形基本相似,满足KBC≈1,表2 只记录了KAB。其中,θ为故障发生时刻相电压相位,θ=90°表示A 相电压峰值时刻发生故障,θ=0°表示A 相电压过零点时刻发生故障;D表示故障点距母线的距离。 表2 的数据表明,故障区段(检测点4)、故障点下游(检测点5、6)部分KAB的值大于Kset1,判断为可能的故障区段。对于可能的故障区段,利用相暂态电流变化量的方向进行辅助判断,根据式(14),计算出的方向参数结果如表3 所示。 表2 谐振接地系统下故障相与健全相暂态电流变化量的比值Table 2 Ratio of transient current change of faulty phase to that of healthy phase in resonant grounded system 表3 电流变化量方向判断Table 3 Direction judgment of transient current change 当图6 中开关S、S1 打开时,仿真模型为中性点不接地系统,对应检测点3 没有电流波形。同样,距母线16 km 处F点发生接地故障,故障发生在A 相电压峰值时刻,故障后一周期各检测点暂态电流变化量波形见附录A 图A2,通过分析各检测点波形,可得出与谐振接地系统类似的结论。通过仿真波形可见,相暂态电流变化量的特征不受接地方式的影响。 中性点不接地系统在不同故障条件下,各检测点经计算后的KAB如表4 所示。对于可能的故障区段,经计算得到的方向参数结果同表3。 表4 不接地系统故障相与健全相暂态电流变化量的比值Table 4 Ratio of transient current change of faulty phase to that of healthy phase in ungrounded system 由表2、表4 可以看出,接地点过渡电阻越大,故障区段故障相与健全相电流的比值越小;该比值受故障发生时刻的影响较小;越靠近母线故障时,比值越大。同时故障区段故障相与健全相暂态电流的比值与系统电容电流的大小有关。当DG 并入配电系统且DG 采用不接地方式时,单相接地故障相暂态波形受DG 的影响较小。 在某10 kV 真型试验场进行了人工单相接地试验,配电网为中性点不接地系统,有4 条主馈线,用集中参数柜模拟实际线路。针对不同的系统电容电流、故障类型做了多次试验。其中,系统电容电流为8 A,C 相发生弧光接地故障时的波形见附录A 图A3;系统电容电流为9 A,C 相发生接地过渡电阻为1 000 Ω 时的波形见附录A 图A4。故障数据来自FTU。利用故障后一周期相暂态电流变化量的数据对本文算法进行了验证,计算每两相暂态电流变化量的比值如表5 所示。试验结果表明,故障区段故障相与健全相暂态电流变化量的比值不小于3,通过式(14)的计算结果表明两者方向相反;健全区段的比值约为1。结果与理论分析一致,同时也验证了本文算法的准确性。 表5 故障相与健全相暂态电流变化量的比值Table 5 Ratio of transient current charge between faulty phase and healthy phase 本文分析了配电网单相接地故障后相电流变化量的稳态、暂态特性,在此基础上了提出了接地故障定位的新方案。通过分析,可以得出以下结论: 1)谐振接地系统采用过补偿方式下,由于故障区段故障相稳态电流变化量的方向与健全相相同,其三相稳态电流变化量差异较小,若只利用相电流变化量的稳态特性定位故障区段,容易出现动作死区。 2)分析相电流变化量的暂态特性可知,一般情况下,故障区段故障相与健全相暂态电流变化量的比值大于等于3;同时,在特征频段内故障区段故障相暂态电流变化量的方向与健全相相反。非故障线路故障相与健全相暂态电流变化量的比值约等于1,且在特征频段内三相暂态电流变化量方向相同。故障点下游故障相与健全相暂态电流变化量的比值难以确定,其大小受系统运行方式、故障点位置、接地点过渡电阻等影响。 3)文中提出一种综合利用相暂态电流变化量比值及方向确定故障区段的定位算法,可以实现接地故障的就地研判。利用故障相与健全相暂态电流变化量的比值可以区分健全区段,利用暂态电流变化量的方向进一步区分故障区段和故障点下游区段。 通过仿真及现场试验结果可以看出,本文方法不受接地方式及故障条件的影响,不需要电压信号及相邻检测点的时间同步,只根据本检测点的三相电流信号即可实现故障定位,达到快速隔离故障的目的,具有较强的工程实用性。 本文通过提取固定特征频段内的相暂态电流变化量信息进行故障区段定位,然而最能反映故障信息的特征频段随线路参数、故障位置等不同而变化,后续将研究可在终端实现的自适应捕捉特征频段算法。 本文研究得到南瑞集团有限公司科技项目“基于国产化的新型配用电端设备关键技术研究与设备研制”的资助,谨此致谢! 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
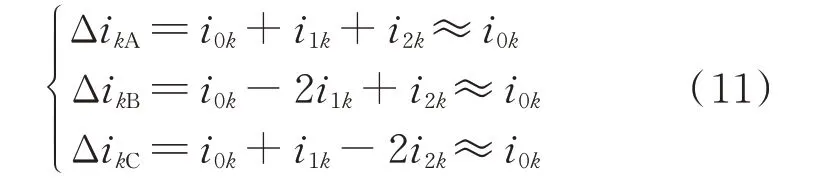
1.4 故障点下游相暂态电流变化量的分析

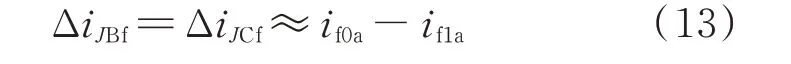
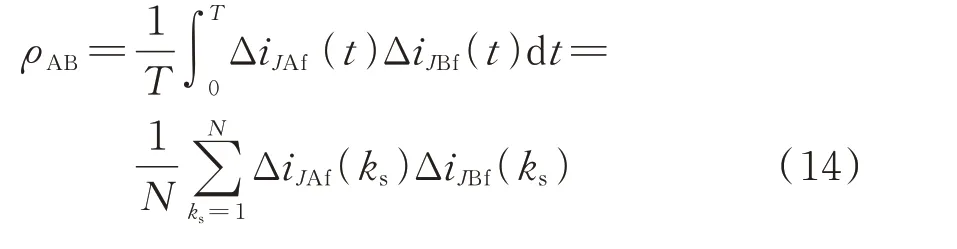
1.5 影响相电流变化量的因素
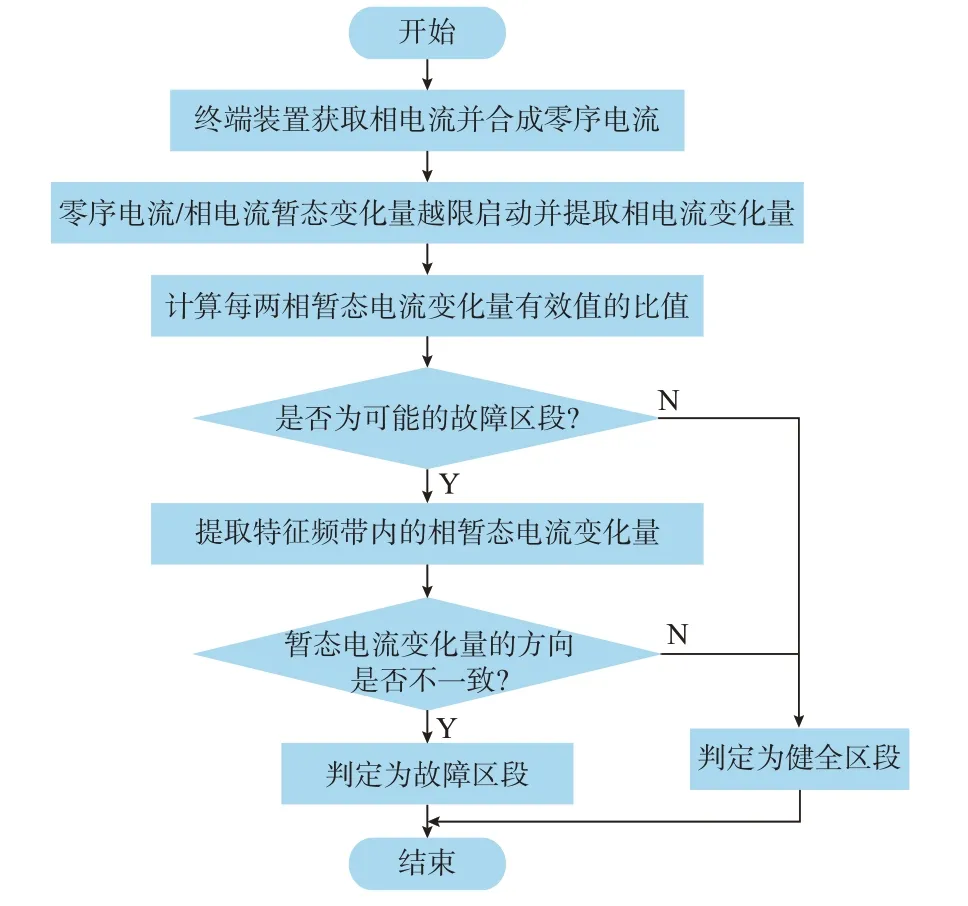
2 基于相暂态电流变化量的区段定位算法
2.1 故障的区段定位算法
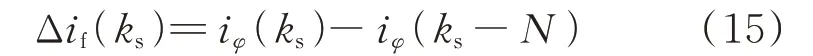
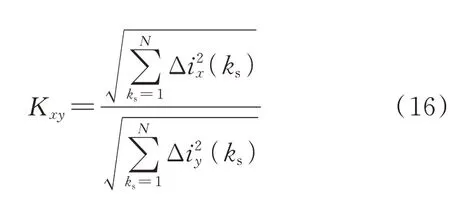
2.2 与现有接地故障暂态检测方法的对比

3 仿真验证及现场试验
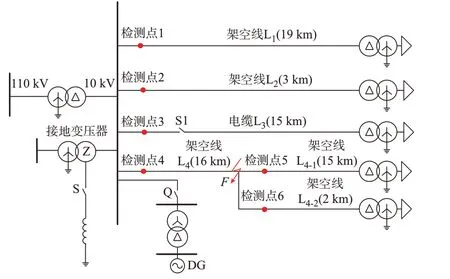
3.1 谐振接地系统故障区段定位算法仿真验证
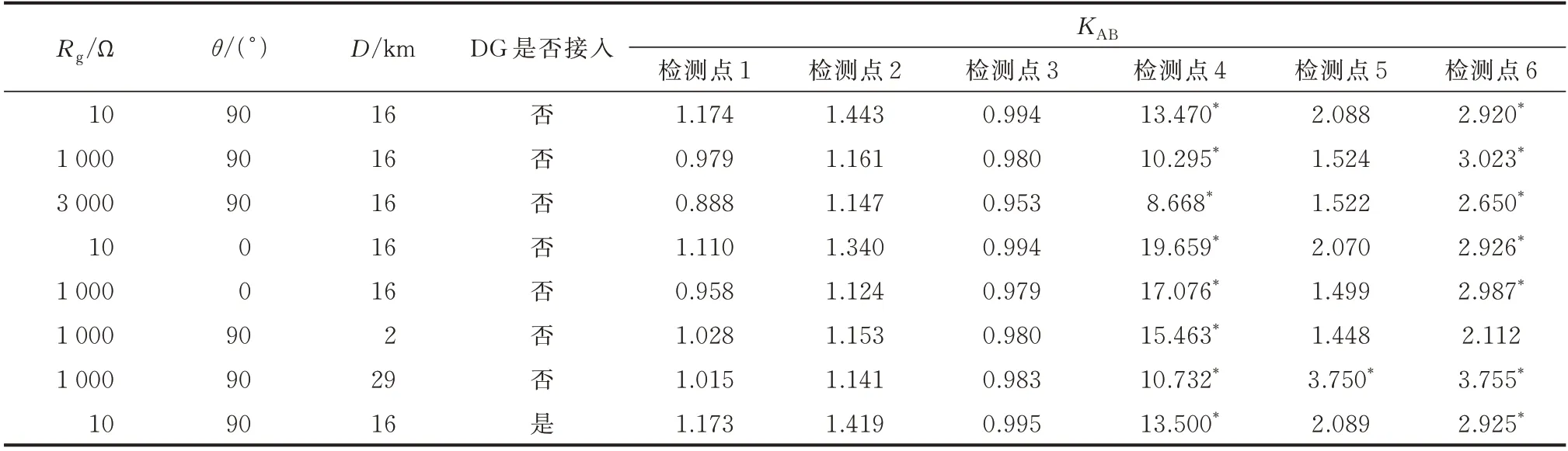
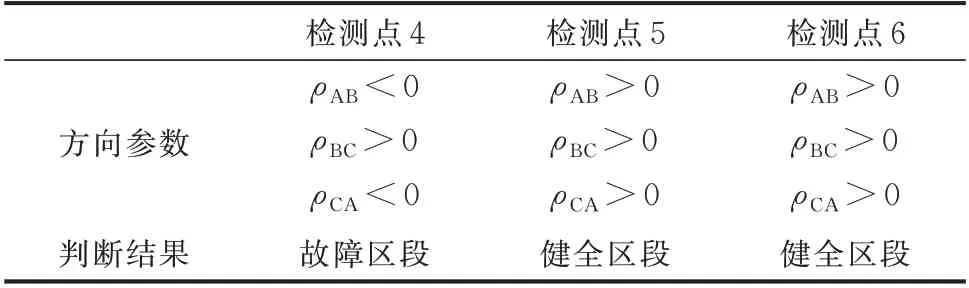
3.2 不接地系统故障区段定位算法仿真验证

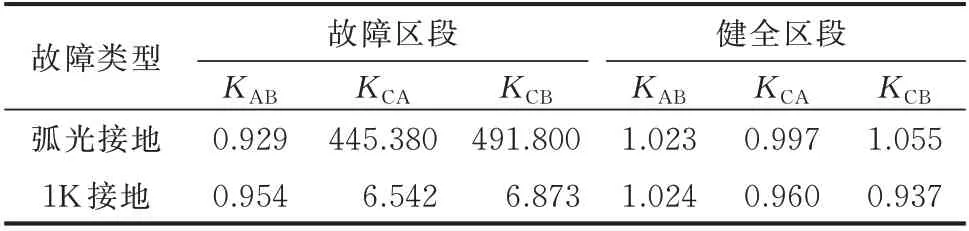
3.3 现场实验
4 结语

