基于电弧随机性和卷积网络的交流串联电弧故障识别方法

巩泉役，彭 克，陈 羽，王 玮，刘发英

（山东理工大学电气与电子工程学院,山东省淄博市 255000）

0 引言

近年来,中国电气火灾占火灾比例约为30%,且呈现上升趋势,已居各类火灾之首［1］。对于民用220 V 交流电而言,电弧电流超过0.5 A 就可能产生明显的拉弧现象［2-3］,故障点处高温会引燃周围易燃物品,导致严重的用电安全事故。低压交流串联电弧故障发生时会使得电路电流减小,导致传统保护装置如断路器、熔断器等并不会动作［4］。因此,如何有效解决低压交流串联电弧故障已成为国内外学者广泛关注与研究的问题［5-6］。

目前,对于低压交流电弧的检测方法主要分为2 类:1）根据发生电弧故障时线路电压［7］、电流［8-9］的变化规律,提出相应的识别方法；2）利用电弧的弧光和弧声［10］、电磁辐射［11］、温度等物理特征检测电弧,但前提是需要事先知道电弧可能发生的具体位置,一般用于对特定开关柜内的电弧进行检测。文献［12-14］利用发生电弧故障时表现的不规则特性检测电弧故障,如电流峰值特性［12］、连续多个周期电流信号丧失严格周期性［13-14］。该类型检测方法虽然实时性强,但难以确定公共阈值。文献［15-16］提出基于傅里叶变换的算法,无论是对电流信号采用分数阶傅里叶变换再进行时频域分析还是提取5 次谐波分量,都具有实时性差、计算量大的缺点。文献［17-18］提出基于小波变换的检测方法,因小波变换是对时间频率的局部化分析方法,易产生频谱混叠问题。文献［19］虽对小波变换进行了大量改进,但变换后的特征量中依旧存在大量冗余信息。文献［20-23］基于人工神经网络、机器学习等提出的检测方法,需要通过大量的训练、筛选才能够保证精准度,并且对数据依赖性大。其中,文献［22-23］提出基于AlexNet 卷积网络的串联电弧故障检测算法。该方法将经过简单滤波或数据清洗后的电流数据以一维数组的形式直接输入网络进行训练,存在训练时间较长、泛化能力不足等缺陷。

针对上述问题,本文提出一种基于电弧随机性和卷积网络的交流串联电弧故障检测方法。该方法利用电弧故障发生时的随机性来提取电弧特征值,并在MATLAB 中构建AlexNet 模型,进一步提高方法的普适性。最后,通过对多种负载和工况进行试验验证了该检测方法的有效性。

1 电弧特征值提取方法的原理

负载在正常工作时,电流相对稳定,周期与周期间相似度高,但发生电弧故障时,由于存在高频随机特性,会使得电流信号中存在一定突变量,周期间相似度低。因此,可通过皮尔逊相关系数r［24］,来体现电流信号周期间的自相关性,如下式所示:

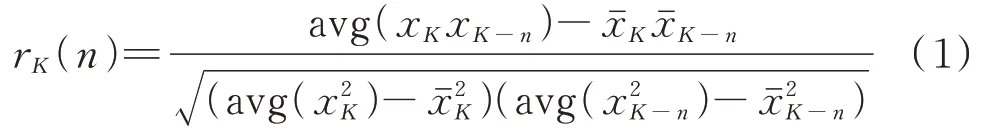
式中:xK和xK-n分别为滤波后K时刻和K-1 时刻的采样电流；xˉK和xˉK-n分别为滤波后K时刻和K-1 时刻滤波后的采样电流平均值；n为当前采样点的值；K为信号总尺度；avg（·）为取均值函数；rK(n)为信号总尺度为K时在采样点n处的皮尔逊相关系数。

rK(n)的大小受电流中的稳态因素影响较大,特别是基频和直流分量,在进行rK(n)的计算前,应减弱电流中基频和直流分量对计算结果的影响,将高频特性进行放大,提出一种以零频率为中心的陷波滤波器充当高通滤波器,其传递函数H(z)如下:

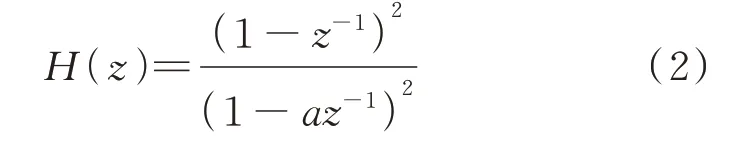
式中:z为xK的频域输入量；a为陷波系数。

该滤波器为一个二阶传递函数,当频率越高时,信号衰减越弱。其中,a取0.77,在经过滤波器以后直流分量可被完全滤除,基频也可得到大幅抑制。

在发生电弧故障时,数据间存在较大的变化率,对其求导后数值会存在较大突变。其一阶导数D可表示为:

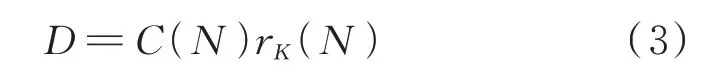
式中:N为滑动窗口长度；C(N)为系数,其值仅随滑动窗口大小N而改变。

固定窗口下C(N)中的每一项均为定值,其提取过程如下:

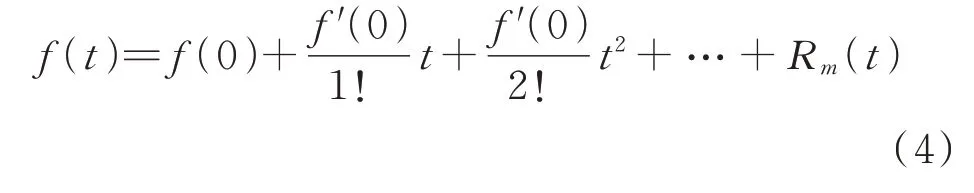
式中:Rm(t)为展开式的拉格朗日余项；m为展开项总数,因仅计算一阶导数,故m取3 即可；f（t）为需要进行泰勒展开的函数；t为时间。

首先,在零点进行m项泰勒展开,然后,进行拉普拉斯变换,通过求导和拉普拉斯反变换［25］得到式（5）,详细推导过程见附录A。

式中:Fs为采样频率；l为步长的累加量,其初始值为0；L为步长的累加量最大值。

综合考虑,在5 kHz 采样率下,滑动窗口N取10,可使信号中所有采样点均参与到计算中去,避免数据中的特征信号在计算中丢失,且对信号中的突变信息最为敏感。采用梯形积分进计算一阶导数,可得到:

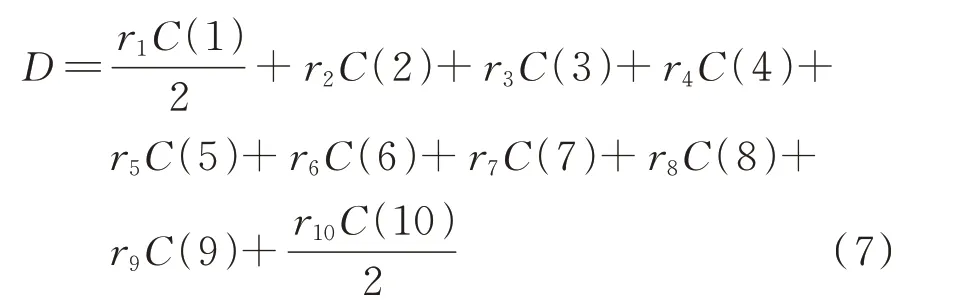
式 中:r1,r2,…,r10分 别 为K取1,2,…,10 时 的 皮 尔逊相关系数。

因滑动窗口N取10,所以在利用式（7）计算相关系数的一阶导数时,相当于求取10 个相关系数间的一阶导数值,取其绝对值作为电弧特征值E,即E=|D|。

2 数据采集及电弧特征值计算

2.1 数据采集及处理

根据GB 14287.4 标准［26］,按照串联碳化路径电弧实验的要求搭建交流串联电弧故障实验电路。该电路由交流电源、断路器、负载、电弧发生器、电流互感器及示波器等构成。图1 为接线图,附录A 图A1为实物图,断路器选用空气断路器,电流互感器变比为3 000∶1,选用Tek-MDO3000 示波器进行电流数据的采集,电弧发生器完全按照标准要求选取和设计,其主要结构由直径为6.4 mm 的碳制固定电极和铜制移动电极、螺旋调节器等组成,螺旋调节器与移动电极相连,用于控制电极间的空气间隙长度。

参照GB 14287.4 标准中的常用典型负载,进行数据采集和分类整理［27］。其中,线性负载有2 种,分别是800 W 电热器阻性负载（记为负载1）、1 000 W电熨斗阻性负载（记为负载2）。非线性负载有8 种,分别是1 500 W 电钻电容启动电机类负载（记为负载3）、2 100 W 电磁炉涡流类负载（记为负载4）、600 W 电脑开关电源类负载（记为负载5）、800 W 微波炉磁控管类负载（记为负载6）、1 000 W 吸尘器串激电机类负载（记为负载7）、800 W 微波炉+800 W电阻组合负载（记为负载8）、600 W 电脑+1 000 W吸尘器组合负载（记为负载9）、36 W 日光灯气体放电类负载（记为负载10）。

首先,对采集到的电流信号利用均值数字滤波器进行消噪处理,得到滤波后的电流频率为5 kHz。交流电弧两端电压和线路电流如附录A 图A2（a）所示,不同典型负载在正常与电弧故障2 种状态下的电流波形如附录A 图A2（b）至图A2（q）所示。然后,利用式（2）对采集到的电脑负载进行陷波滤波,滤波后的电流信号中以高频成分为主,滤波效果如附录A 图A3 所示。

2.2 电弧特征值计算

对经过陷波滤波得到的电流信号进行相关系数r的计算,结果如附录A 图A4 所示。对多数负载而言,在正常工作时,滤波后的皮尔逊相关系数趋近于1,而在发生电弧故障时则低于0.96。但对于少数负载而言,如电脑负载,其相似度值相较于电热器负载、微波炉和电阻组合负载而言,要更低一些,在0.88～0.93 范围内；当发生电弧故障时,相关系数在0.75～0.85 范围内。虽然从数值上可有效区分这2 种状态,但与其他负载间存在数据交叉现象。利用式（7）对相关系数进行电弧特征值的计算时,结果如图2 所示。

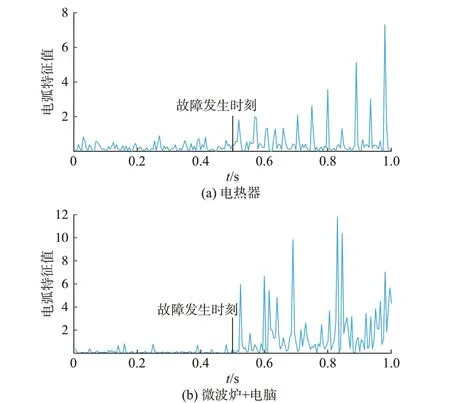
图2 不同负载电弧特征值计算结果Fig.2 Calculation results of arc characteristic value with different loads

由图2 可知,当负载正常运行与发生故障时,电弧特征值存在较大差异。在负载正常工作时,相关系数基本不变,电弧特征值趋近于0；在发生故障时,相关系数浮动较大,电弧特征值存在数值突变。经大量实验数据分析,阈值取1 时,可有效判别电弧故障。

2.3 检测方法对比

根据GB 14287.4 规定,如果1 s 内发生14 个及以上半周期的电弧故障时,要求电弧故障断路器应在30 s 内发出警报信号。选取10 种典型电器及其组合,各采集100 组1 s 时长的有效电流数据进行电弧故障检测,其中,对于每种负载数据,故障50 组,非故障50 组。对比文献［12］（记为方法1）、文献［17］（记为方法2）、文献［28］（记为方法3）以及本文方法的检测结果,如表1 所示。

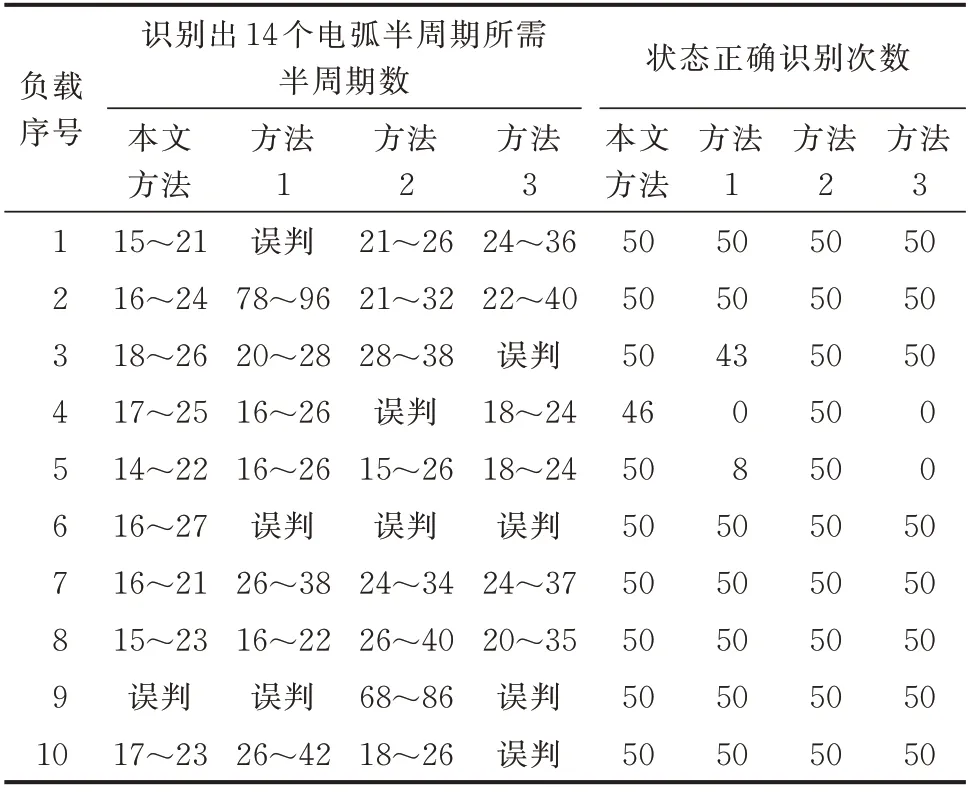
表1 4 种方法的检测结果Table 1 Detection results of four methods

由表1 可知,在10 种典型负载正常工作时,本文方法仅对50 组电磁炉负载（负载4）产生4 次误判,其余9 种负载均未发生误判,与其他3 种方法相比,所产生的误判最少。根据GB 14287.4 标准,在发生电弧故障时,出现误判或识别出14 个电弧半周期所需半周期数超过100 个,即认为该算法不适用于该负载类型。与其他3 种方法相比而言,本文方法对10 种典型负载的电弧半周期数识别精度最高、适用种类最多,仅对吸尘器+电脑负载（负载9）无法做到有效判别。

通过计算吸尘器+电脑负载的电弧特征值（见附录A 图A5）可知,在发生故障时,该负载的电弧特征值在0.3 左右,并不满足1 的阈值标准,与其他负载正常情况下的电弧特征值出现交叉现象。因此,有必要采用AlexNet 模型对电弧特征值进行特征提取,以提升算法的普适性。

3 AlexNet 模型结构与电弧故障检测算法

3.1 AlexNet 模型结构

传统的AlexNet 模型由5 个卷积层、3 个池化层和3 个全连接层构成。卷积层可用于提取局部特征,池化层可用于特征压缩并提取主要特征,全连接层则用于分类。传统的AlexNet 模型参数规模较大,计算成本高。因此,采用卷积拆分和分组卷积的方式可降低卷积核参数数量,全连接层采用全局平均池化完成特征向量化,采用PReLU 激活函数,因增加了一个参数修正环节,可有效避免参数众多问题［29］。本文所用的AlexNet 模型架构如图3 所示。

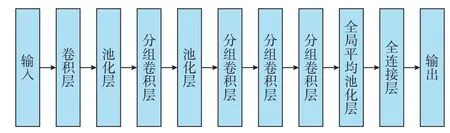
图3 AlexNet 模型架构Fig.3 Architecture of AlexNet model

3.2 基于AlexNet 模型的电弧故障检测方法

故障前后,本文算法中电弧特征值有较大区别,即存在多处突变。因此,在采集电流数据时,需保留一段故障发生时刻之前的电流数据,在进行一维卷积运算时可以突出发生电弧故障时多处突变的特征信息,并融入卷积运算中。为了更加直观地呈现输入样本,分别取一组正常和故障样本生成图像,如附录A 图A6 所示,实际输入是以一维数组的形式表示。

采样信号xk如附录A 图A7 所示。其中,xk1为故障检测点之前的电流数据,xk2为故障发生时刻之后的电流数据。根据GB 14287.4 规定的1 s 内需检测到14 个及以上故障电弧半周期的标准,考虑到本文方法识别出14 个电弧半周期所需半周期数均在30 个以内,因此,为保证算法的高时效性,采样信号xk时间尺度取0.4 s,其中,xk1时间尺度取0.1 s,xk2取0.3 s,即本文方法在故障发生后的0.3 s 时进行故障判别。在0.4 s 的时间尺度和5 kHz 的采样频率下,将电弧特征值E生成数组,作为模型的输入量,其尺度大小仅为1×400。

基于AlexNet 模型的电弧故障检测方法流程如图4 所示。

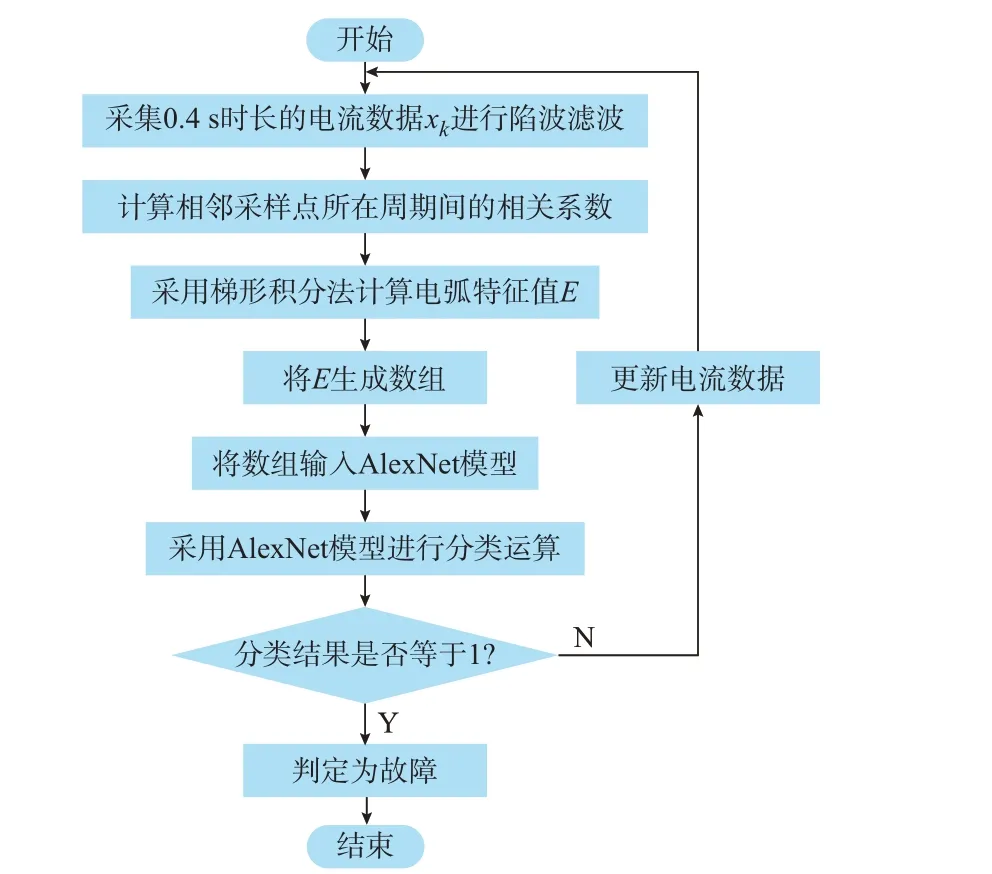
图4 基于AlexNet 模型的电弧故障检测方法流程图Fig.4 Flow chart of arc fault detection method based on AlexNet model

4 试验验证与分析

4.1 AlexNet 模型分析

对10 种典型负载分别采集110 组0.40 s 的电流数据,其中55 组正常、55 组故障,电弧故障发生时间为0.1 s。每种负载类型各抽取50 组故障数据和50 组正常数据作为训练集,共1 000 组训练数据。每种负载类型剩余的5 组故障数据和正常数据作为测试集,共100 组。

在MATLAB 中搭建AlexNet 模型并进行训练,训练结果如图5 所示。由图5 可知,在迭代了100 次以后训练准确率开始趋近于1,并稳定在99.7%附近,同时,网络的损失值也在不断下降。在迭代120 次以后,模型开始收敛,模型总训练时长为17.56 s。总体而言,AlexNet 模型训练过程简单且准确率高。

AlexNet 模型对100 组测试集的识别结果如图5（c）中的混淆矩阵所示,可知模型对测试集中电弧故障的识别率为100%,无任何误判情况。

图5 AlexNet 模型训练效果Fig.5 Training effect of AlexNet model

为了进一步验证AlexNet 网络与电弧特征值构成的特征矩阵之间的适应程度,采用交叉验证的方式测试模型性能,即对10 种典型负载重新采集和生成3 000 组训练数据,随机抽取1 000 组作为训练集,100 组作为测试集进行训练,重复50 次,统计训练结果。经过50 次的交叉验证,准确率达到99.5%以上的最少迭代次数为65 次,最大迭代次数为187 次；对测试集的检测结果最低识别率为99%,即误判1 次,共出现3 次,其余情况均为100%识别。

4.2 AlexNet 模型性能检测

为了进一步验证AlexNet 模型对训练集负载类型进行故障检测的可靠性,对10 种典型负载重新各采集50 组有效的数据,利用在MATLAB 中构建好的AlexNet 模型对实测数据进行电弧故障检测。其中,对于每种负载,分别为25 组故障数据,25 组非故障数据,共500 组数据。AlexNet 模型对10 种典型负载均可有效地完成状态分类,实现电弧故障识别,仅对电钻负载出现3 次误判,虽无法做到100%训练集负载类型都可检测,但较其他检测方法,已具备较高检测精度,检测精度可达99.4%。

对于10 种典型负载而言,在发生电弧故障时,同一负载下,不同工频半周期内的燃弧电压的值并不完全相同,故不同组别间的故障电流数据存在较大差异。但在负载正常工作时,数据较为稳定,因此,有必要改变负载功率大小,进一步对方法进行验证。对改变功率后的10 种典型负载重新各采集50 组有效的数据,其中,对于每种负载,分别为25 组故障数据,25 组非故障数据,共500 组数据。此时,AlexNet 模型的检测性能稍微变差。对于电脑负载而言,误判均来自内部整流线路等控制电路的影响,均发生在负载正常阶段；对于日光灯负载而言,由于功率较小,导致信号受线路、设备和环境影响较大,因此存在几次误判。

总之,改变负载功率大小对AlexNet 模型的检测性能影响较小,主要是负载本身特性所产生的影响。在实际工作中,民用电负载种类复杂多变,经常会出现线路参数相差较大和未知负载的情况。线路长度不同,其电气参数就不同,电源的谐波含量也就不同。因此,为了进一步检验AlexNet 模型的检测性能和普适性,采集10 种典型负载在不同线路长度下的电流数据各50 组,故障25 组,非故障25 组,代入模型进行检测。测试结果（见附录A 表A1）表明,本文提出的检测方法能够适用于不同长度的线路,改变线路参数对本文提出的检测方法基本无影响。

采集8 种未参与模型训练的负载类型各50 组有效电流数据进行检测,其中,每类负载数据均为故障25 组、非故障25 组。对非训练集负载类型,采用AlexNet 模型的检测结果如表2 所示。

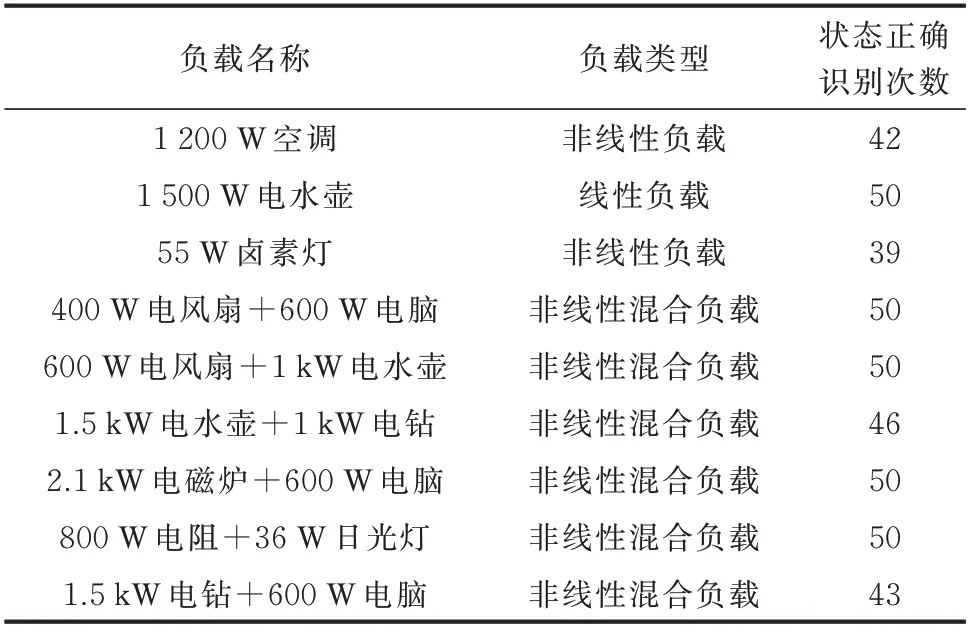
表2 非训练集负载类型的AlexNet 模型检测结果Table 2 Detection results of non-training set load with AlexNet model

如表2 所示,卤素灯负载的误判较多,原因在于0.4 s 的采样信号中,故障发生后的0.3 s 中,信号中的电弧特征信息较少,误判主要来自故障信号。对于空调、1.5 kW 电水壶+1 kW 电钻、1.5 kW 电钻+600 W 电脑3 种负载而言,误判产生的主要原因在于正常信号中扰动较大,存在电弧特征值的突变现象,但突变信息并不是神经网络进行故障判别的唯一特征信息,仅是网络在进行特征提取时的影响因素之一,因此仅存在几次误判。在实际工程应用中,可以通过对训练集种类的不断补充来不断优化模型的检测效果。

总之,本文提出的故障检测模型对训练集负载和非训练集负载都具有较高的识别精度,算法的总体识别精度可达98.5%以上,且满足了GB 14287.4标准所规定的要求。

4.3 AlexNet 模型抗干扰分析

对计算机启动电流进行电弧特征值的计算,结果如附录A 图A8 所示。在电源打开后到计算机稳定运行阶段,共60 个电流半周期,存在4 次超过阈值1 的情况,在之后的140 个电流半周期,即计算机稳定运行阶段,无任何误判。

附录A 图A9 为电热器稳定运行时接入微波炉负载的过程。对该过程的电流进行电弧特征值的计算,结果如图A9（b）所示,在电热器稳定运行的1.25 s 内,共出现1 次超过阈值的情况。从接入微波炉到混合负载稳定运行阶段,电弧特征值共出现6 次超过阈值的情况,其中,2 次来自刚接入微波炉阶段,且突变电流值较大；4 次来自即将达到稳定运行阶段。平稳运行阶段电弧特征值未发生超过阈值的情况。

将计算机和混合负载的启动电流数据输入AlexNet 模型进行检测,虽然在第255 个电弧半周期处存在较大突变,但在0.4 s 的计算窗口下,对于计算机和混合负载的启动过程,各阶段电弧特征值超过阈值次数远低于14 次。因此,即便信号中存在较大突变,但未对AlexNet 模型的检测产生影响。

附录A 表A2 为采用AlexNet 模型对典型负载启动过程进行检测的结果,每种负载各采集10 次启动过程数据。检测结果表明,提出的AlexNet 模型可有效排除负载启动过程对故障识别的影响,无误判发生。

5 AlexNet 模型对比分析

本文方法与文献［22-23］中的方法比较结果如表3 所示,其中,文献［22］的方法（记为方法4）和文献［23］的方法（记为方法5）也是基于AlexNet 模型的检测方法。

表3 基于AlexNet 模型的3 种检测方法对比Table 3 Comparison of three detection methods based on AlexNet model

由表3 可知,本文方法训练集数量为1 000 组,且单组数据尺度仅为1×400,与其他2 种方法相比,大大压缩了训练集数量和数据维数,且精度也高于其余2 种方法。方法4 和方法5 因没有进行特征信息的提取,完全依靠原始电流数据进行训练,势必会产生非训练集负载和负载启动过程对模型存在较大影响的情况。总体而言,本文利用电弧特征值训练的AlexNet 模型鲁棒性更强。

6 结语

针对低压交流串联电弧故障隐蔽性强、严重威胁民用场合下用电安全的问题,本文提出一种基于电弧随机性和AlexNet 模型的交流串联电弧故障识别方法。建立的基于AlexNet 模型的电弧故障检测方法可进一步提升电弧故障检测的普适性,且将电弧特征值作为模型的输入,可压缩特征向量维数,放大电弧特征信息,使得训练过程简单,较好地融合了传统算法与神经网络的优点,提升了低压交流串联电弧故障识别精确度。改变环境温度、湿度、增设屏蔽性负载等同样会影响电弧故障特性,受实验条件限制,本文未对上述工况进行试验验证,在后续工作中将进一步加以考虑。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。