面向综合能源系统的㶲流计算模型

李家熙，王 丹，2，周天烁，贾宏杰，2

（1. 智能电网教育部重点实验室（天津大学）,天津市 300072；2. 天津市智慧能源与信息技术重点实验室（天津大学）,天津市 300072）

0 引言

日益突出的社会环境和资源问题导致全社会对高效绿色能源需求日趋迫切,综合能源系统（integrated energy system,IES）作为多能利用的一种形态,得到了社会各界的广泛关注［1-2］。IES 涉及多种能量形式,不同能量的品质存在差异。㶲作为衡量能量品质的一种量度,兼顾了能量的“量”和“质”,被广泛引入能源系统的研究。

目前,关于㶲的研究大多集中在某一具体能源转换环节中㶲的变化情况。例如,文献［3］将㶲分析引入发电系统,建立光伏、风机、水力等多能互补发电系统的㶲分析模型；文献［4］针对伊朗伊斯法罕某一发电厂中的蒸汽循环过程,基于㶲平衡方程分析了锅炉、涡轮、冷凝器等各个循环设备的㶲情况；文献［5］针对园区级IES,采用能质系数建立㶲分析模型,基于图论求解各个能源设备的㶲分布。

部分IES 㶲分析研究将系统视为“黑箱”模型,以㶲效率作为系统规划、运行、评估的一项核心指标。其中,文献［6］采用基于能质系数的㶲分析方法,计算系统输入和输出㶲,引入㶲效率构建多目标规划模型；文献［7］引入能量的折算系数求解㶲效率,并将㶲效率作为系统优化调度的一项目标。此外,部分研究开始分析IES 内部的㶲损情况,文献［8］建立了㶲在多能管线中的传递理论,以总㶲损作为系统优化的目标函数；文献［9］建立了能源站㶲损模型,研究了以最小化总㶲损为目标的多站联合运行优化调度模型。

上述研究中,无论是具体能源转换环节的㶲变化分析,还是㶲效率和㶲损分析,均未考虑㶲在能源网络中的分布特征,类比能流、碳流、信息流等研究对象,具有网络化特征的IES 同样可以构建㶲流理论,以便分析更为精细的系统能源品质特征。目前,已有一些关于单一能源网络的㶲分析研究,如文献［10］建立了区域热力系统的㶲分析模型,但未考虑电力、天然气、热力系统之间耦合因素的影响,无法适应IES 的㶲流建模。

目前,已有部分研究基于“势”和“流”的角度分析IES 中某种流量的分布。例如,文献［11-12］针对电力、天然气、水力、热力能流模型,定义了与能流有关的“流”和“势”的概念,其中,“流”参数包括电流、气流、水流、热流,“势”参数包括电压、气压、水压、温度。类似地,IES 㶲流分布同样可以基于“势”和“流”的角度进行分析。对此,文献［13］以电流、气流、水流等介质参数为“流”参数,基于传统㶲计算方法［14］与电路理论中的电势概念［15］,定义了IES 㶲流分析的“势”参数。与电势和电势差的物理含义［15］类似,㶲势反映了单位介质承载的㶲,㶲势差反映了单位介质传递的㶲。基于上述“流”与“势”的概念,文献［13］提出了IES 能源网络㶲流机理模型,通过整体和局部㶲平衡分析以及与传统㶲分析方法的对比,验证了模型的合理性和优越性。

文献［16-18］分别建立了多能流、碳流、信息流计算模型,实现了能源网络中能量流、碳流、信息流的高效求解。类似地,基于IES 㶲流机理,建立IES㶲流计算模型是获取大规模系统㶲流分布,以及量化能源品质研究的重要基础。基于IES 㶲流计算模型,决策者可计算各能源网络有效能的流动及损耗情况,追踪高品质能量流动轨迹,进而做出改善系统能源品质的优化决策。

考虑到目前关注IES 网络㶲流分布的研究较少,对于较大规模的系统㶲流分析缺乏合适的矩阵化计算方法,本文基于文献［13］提出的IES 㶲流机理,提出了不同场景下IES 㶲流矩阵化计算模型:1）若系统某些位置能流或功率已知,即非平衡节点功率已知场景下,以介质流为支路参数,㶲势为节点参数,建立了矩阵化间接计算模型；2）若系统某些位置的源荷㶲可以测算,即非平衡节点㶲已知场景下,建立了介质流与㶲流之间的联系,构建㶲集线器模型描述能源耦合环节,提出了矩阵化直接计算模型。最后,通过算例系统验证了两种模型的正确性、合理性、优越性,分析了系统的能源品质特征。

1 基于非平衡节点功率的㶲流间接计算模型

本文研究的典型IES 包括电力、天然气、热力系统以及能源站设施。文中涉及非平衡节点功率是指电力、天然气、热力系统除平衡节点［19］之外的源荷功率,源荷功率为源端供应功率与负荷消耗功率的统称,包括电源、气源、热源分别供应的电功率、气功率、热功率,以及电负荷、气负荷、热负荷分别消耗的电功率、气功率、热功率。本章基于IES 㶲流机理模型和分析方法［13］,提出基于非平衡节点功率的㶲流计算模型。已知非平衡节点功率可先求解系统多能潮流,进而计算㶲流相关变量,实现㶲流间接求解。以下分别针对各能源系统说明具体求解步骤,所有变量均以矩阵、向量形式描述。

1.1 基于潮流分布的电力系统㶲流间接计算模型

基于电力系统㶲流机理模型［13］,电力系统㶲流分布包括电力线路㶲流、电力线路㶲损、电源供应㶲、电负荷消耗㶲,以向量形式描述㶲流,电源供应㶲和电负荷消耗㶲统称为电力源荷㶲。电能为最高品质能源,可全部视为㶲［14］。因此,电力系统潮流计算模型即为㶲流模型,线路㶲流、㶲损和源荷㶲可表示为:

式中:ee、Δee、Pe和ΔPe分别为ne,l维电力线路㶲流、电力线路㶲损、传输有功功率和有功损耗列向量,ne,l为电力线路数目；ee,N和Pe,N分别为ne,n维电力源荷㶲和源荷功率列向量,负荷对应元素为正值,电源对应元素为负值,连接节点对应元素为0,ne,n为电力节点数目。

在已知非平衡节点功率的条件下,采用如牛顿-拉夫逊法（下文简称牛拉法）、PQ分解法和前推回代法等算法求解有功潮流分布,即可获得电力系统㶲流分布,有功损耗为㶲损,电压为电力系统㶲势［13］。

1.2 基于气流分布的天然气系统㶲流间接计算模型

基于天然气系统㶲流机理模型［13］,天然气系统㶲流分布包括天然气管道㶲流、气源供应㶲、气负荷消耗㶲,以向量形式描述㶲流,气源供应㶲和气负荷消耗㶲统称为天然气源荷㶲。

天然气网络分析常以非平衡节点气流率为已知量,表征气源提供或负荷消耗的功率［20］,基于燃气系统能流求解管道气流率分布。基于文献［13］中的天然气系统㶲流机理模型,将燃料㶲等效为天然气燃烧过程中从环境温度变为理论燃烧温度放出的热量㶲［21-23］,天然气系统㶲流可表示为天然气节点㶲势与气流率的乘积。采用矩阵的形式表示天然气系统的㶲流计算模型:

式中:Ta和Tb分别为环境温度和天然气的理论燃烧温度；G为天然气的热值。

1.3 基于水流分布的热力系统㶲流间接计算模型

基于热力系统㶲流机理模型［13］,热力系统㶲流分布包括㶲损、热源㶲和热负荷㶲、元件㶲流。其中,㶲损包括供回水管道㶲损和热负荷㶲损,热负荷㶲损是由热负荷出口与回水节点的㶲势差导致的；热源㶲和热负荷㶲分别为热源供应㶲和热负荷消耗㶲,统称为热力源荷㶲；元件㶲流包括供回水管道㶲流、流入热源㶲流、流入负荷㶲流和流出负荷㶲流。

在已知热负荷的情况下,基于热力潮流计算求解管道水流率以及供水、回水和出口节点水温,进而获得各节点的㶲势,基于㶲势和水流率求解㶲流及㶲损分布［13］。根据节点处水温T、环境温度Ta,定义热力系统的节点㶲势pT为［13］:

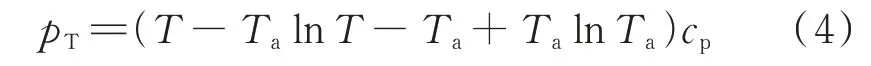
式中:cp为水的比热容。

根据节点㶲势和水流率,计算元件㶲流和元件传递热量㶲。其中,元件㶲流为㶲势与水流率的乘积,元件传递热量㶲为㶲势差与水流率的乘积［13］:

式中:eh为元件㶲流；mh为水流率；Δeh为元件传递热量㶲,包括㶲损与热力源荷㶲；ΔpT为元件两端节点㶲势差。由式（5）可知,pT反映单位水流率承载的㶲,ΔpT反映单位水流率传递的热量㶲。

由式（5）可得,对于规模化热力系统,热源㶲为供水与回水节点㶲势之差与水流率的乘积。采用矩阵的形式可表示为:

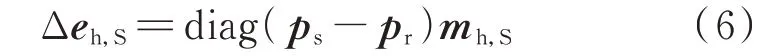
式中:Δeh,S为nh,n维热源㶲列向量,nh,n为供水节点数目；diag（·）表示以向量中的元素构成的对角矩阵；ps和pr分别为nh,n维供水和回水节点㶲势列向量；mh,S为nh,n维热源水流率列向量,当第i个节点为热源供水节点时,mh,S的第i个元素为此节点的水流率,其他元素为0。本文选取供水至回水节点的水流方向为正,mh,S和Δeh,S的非零元素为负值。

同理,热负荷㶲可表示为供水与回水节点㶲势之差与水流率的乘积。采取矩阵的形式可表示为:

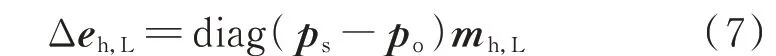
式中:Δeh,L为nh,n维热负荷㶲列向量；po为nh,n维出口节点㶲势列向量；mh,L为nh,n维热负荷水流率列向量,当第i个节点为负荷供水节点时,mh,L的第i个元素为此节点的水流率,其他元素为0。mh,L和Δeh,L的非零元素为正值。

热力系统中,部分热负荷出口节点㶲势和回水节点㶲势存在差异,故产生热负荷㶲损,该部分㶲损可以表示为出口、回水节点㶲势之差与水流率的乘积。采用矩阵的形式可表示为:

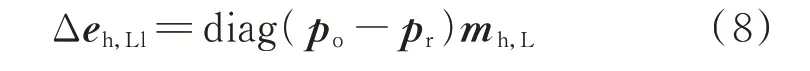
式中:Δeh,Ll为nh,n维热负荷㶲损列向量。

借助节点-支路关联矩阵［24］描述系统拓扑,基于式（5）,对于规模化热力系统,供水管道两端的㶲势差可由节点-支路关联矩阵与节点㶲势向量表示,则供水管道㶲损可表示为:

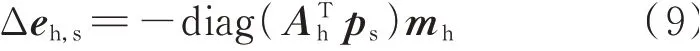
式中:Δeh,s为nh,p维供水管道㶲损向量,nh,p为供水管道数目；mh为nh,p维供水管道水流率列向量；Ah为nh,n×nh,p供水网络节点-支路关联矩阵。

假设供水网络和回水网络完全对称,且忽略水流损失,则回水网络的节点-支路关联矩阵可视为-Ah。同理,回水管道㶲损向量Δeh,r可表示为:

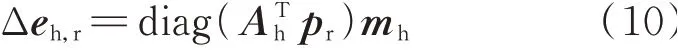
由式（5）可知,供回水管道㶲流主要由管道中水流出节点的㶲势决定,可定义供水网络流出节点-支路关联矩阵、流入节点-支路关联矩阵,用于表征支路和流出、流入节点的拓扑关系［12］。

其中,流出节点-支路关联矩阵Ah,-中的元素可表示为:

式中:(i,j)表示矩阵第i行、第j列的元素。

受供回水网络对称性的影响,供水网络的流入节点-支路关联矩阵Ah,+即为回水网络流出节点-支路关联矩阵,其元素为:

基于上述关联矩阵、节点㶲势列向量、供水管道水流率列向量,可用矩阵的形式分别表示供水和回水管道㶲流:

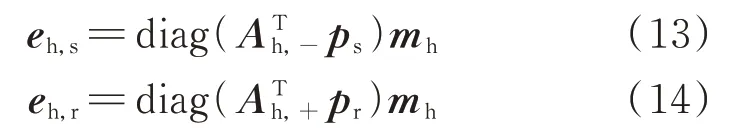
式中:eh,s和eh,r分别为供水和回水管道nh,p维㶲流列向量。

综上所述,基于热力潮流求解水流率和各节点水温,构建供水、回水和出口节点㶲势向量,采用式（6）—式（14）求解规模化热力系统的㶲流分布。

1.4 基于等效节点的能源站㶲流间接计算模型

电力、天然气和热力系统通过能源站实现能源转换,涉及能源品质的改变,即产生㶲损。能源站可等效为电力、天然气和热力节点的集成形式,在多能潮流结果的基础上,通过各能源系统㶲流计算模型可获取能源站等效节点的㶲流,将能源站等效为㶲损节点。采用向量形式表示能源站㶲损［13］:

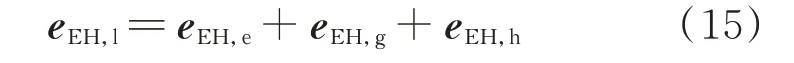
式 中:eEH,l为 能 源 站 节 点 㶲 损 列 向 量；eEH,e、eEH,g和eEH,h分别为能源站对应电力、天然气和热力（热源㶲或热负荷㶲）相连节点的㶲流列向量,维数为能源站数目,若第i个能源站没有第k种能源形式的相连节点,则eEH,k的第i个元素为0,即

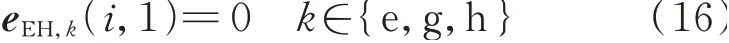
1.5 基于非平衡节点功率的㶲流间接计算模型

综上所述,在非平衡节点功率已知的情况下,IES 㶲流求解可建立在多能流计算结果基础上,基于电力潮流、天然气流率、节点温度、水流率等多能流参数,获得IES 㶲流分布。本文选取“以热定电”的IES 运行模式展开分析,具体计算流程如图1所示。

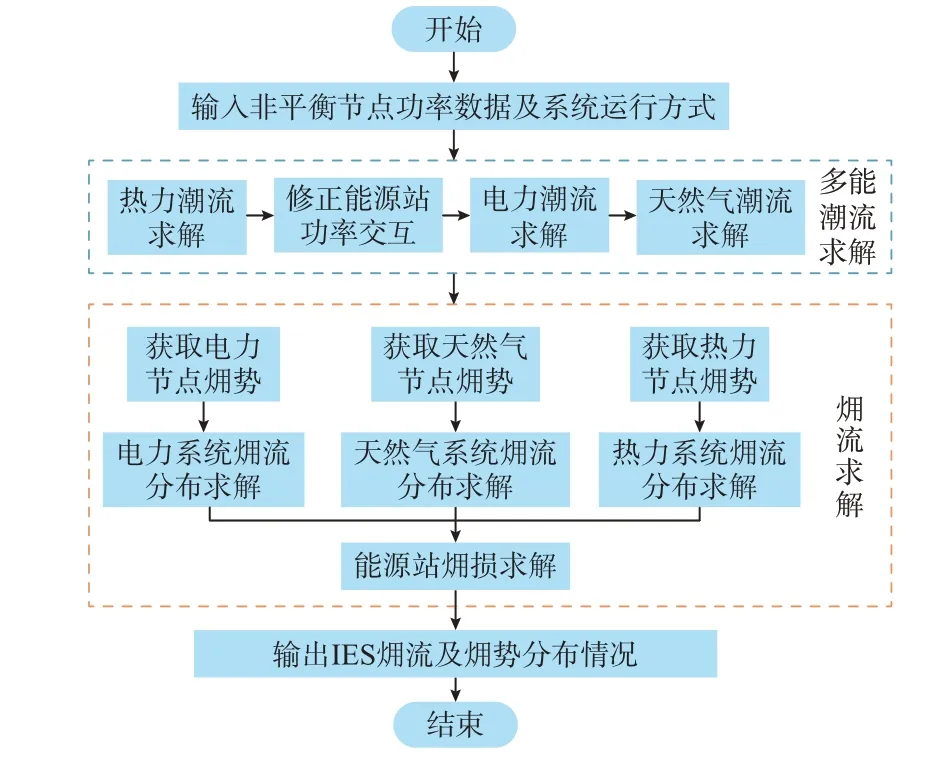
图1 基于非平衡节点功率的㶲流间接计算模型Fig.1 Indirect calculation model of exergy flow based on power of unbalanced nodes

1）基于非平衡节点功率、网络拓扑、管线参数、能源站设备型号及运行方式等数据,选取合适的多能流计算模型,求解IES 中的电力潮流,天然气流率,热力系统的供水、回水和出口节点温度以及水流率等；

2）通过电压、电力潮流、电负荷获取电力系统㶲势、电力线路㶲流、电力线路㶲损、电力源荷㶲；

3）计算天然气节点㶲势,由天然气流率向量得到天然气管道㶲流、天然气源荷㶲；

4）根据热力系统各节点温度获得供水、回水和出口节点㶲势向量,通过节点㶲势和水流率向量求解热力系统的㶲流分布,包括元件㶲流、㶲损、热负荷㶲和热源㶲；

5）根据电力源荷㶲、天然气源荷㶲、热力源荷㶲计算能源站等效节点㶲流列向量,进而获得各能源站等效节点㶲损；

6）最后,形成IES 整体㶲流及节点㶲势分布。

2 基于非平衡节点㶲的㶲流直接计算模型

非平衡节点㶲是指电力、天然气、热力系统除平衡节点之外的源荷㶲,源荷㶲为源端供应㶲与负荷消耗㶲的统称,即上述电力源荷㶲、天然气源荷㶲、热力源荷㶲的统称。非平衡节点㶲可以通过若干种方式获得。例如,基于IES 㶲流机理模型［13］,源荷㶲可表示为介质流与节点㶲势的复数乘积（电力）或实数乘积（天然气、热力）形式,通过源荷位置介质流的量测装置测算源荷电流、气流、水流等,量测电压、供水温度等㶲势计算参数估计节点㶲势,进而间接测算非平衡节点的源荷㶲。该场景没有测算能流或功率,故㶲流间接计算方法不再适用。针对上述场景,可建立IES 各能源环节的㶲流计算模型,以获取系统整体㶲流分布。

2.1 电力系统三相㶲流直接计算模型

基于电力系统㶲流机理模型［13］,电力系统有功潮流为㶲流,有功线损为㶲损,如果非平衡节点㶲已知,表示非平衡节点功率已知。此时,电力系统三相㶲流计算模型可由潮流模型［25］得到,表示如下:

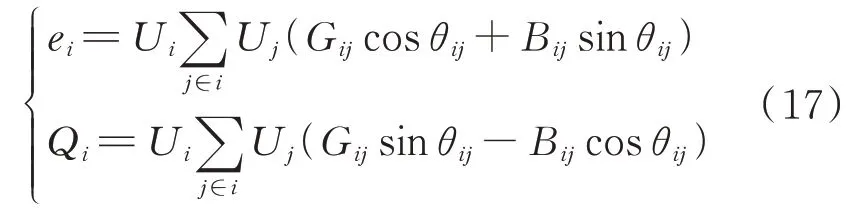
式中:ei和Qi分别为节点i的㶲流和无功功率；Ui和Uj分 别 为 节 点i和j的 电 压；j∈i表 示 节 点i和j相连；Gij和Bij分别为节点i和j间线路的电导和电纳；θij为节点i和j电压相角差。

基于有功损耗计算公式,节点i与j之间电力线路的㶲损Δee可表示为:

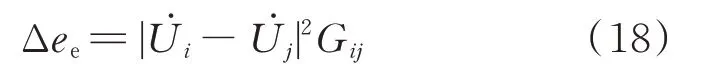
式中:U̇i和U̇j分别为线路两端的电压相量；|⋅|表示复数取模或实数取绝对值。

式（17）可采用牛拉法、PQ分解法、前推回代法等算法求解,本文不再赘述。

2.2 天然气系统气压-㶲流直接计算模型

基于天然气系统㶲流机理模型［13］,天然气㶲流等于㶲势与气流率的乘积,㶲势由天然气参数和环境温度得到,可视为常数,天然气流率在节点处满足广义化的基尔霍夫第一定律［20］,㶲流在节点处同样满足广义化的基尔霍夫第一定律,可采用节点㶲流方程表示:

式中:Ag为ng,n×ng,p天然气系统的节点-支路关联矩阵。

低压、中压和高压天然气系统可分别采用Lacey 方程、Polyflo 方程和Panhandle“A”方程来表示节点气压和气流率之间的关系［26］。将式（2）代入3 类气压-气流方程,可得到表征不同气压等级下节点气压与管道㶲流关系的气压-㶲流方程:

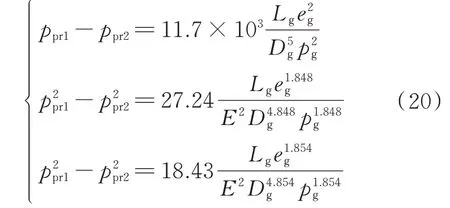
式中:ppr1和ppr2为管道两端的气压；eg为管道㶲流；Dg为管道直径；Lg为天然气管道长度；E为效率因子。式（20）中的3 个式子分别可称为:类Lacey 㶲流方程、类Polyflo 㶲流方程和类Panhandle“A”㶲流方程。

类比天然气潮流求解思路,式（19）和式（20）构成的气压-㶲流计算模型可采用牛顿节点法求解,具体求解流程如附录A 所示。

2.3 热力系统水力-热力-㶲流直接计算模型

IES 多能流研究中,热负荷为已知量,能流、负荷都与温度、水流率有关,热力潮流可采用水力、热力模型交替迭代的方法求解。同理,基于热力系统㶲流机理模型［13］,㶲流、负荷㶲都与㶲势、水流率有关,而㶲势又与温度有关。因此,同样可采用水力模型、热力-㶲流模型交替迭代的方法求解热力系统㶲流分布。

2.3.1 水力模型

热力系统中水作为传递㶲的介质,是影响㶲流、㶲损和负荷㶲的重要参数,水流分布的获取在㶲流计算中十分重要。水流在节点处满足广义化的基尔霍夫第一定律,水压在环路内满足广义化的基尔霍夫第二定律,可采用流量连续方程和水压降落方程描述［27］:

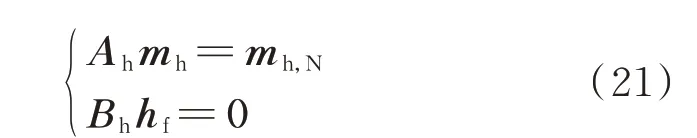
式中:Bh为nh,l×nh,p回路-支路关联矩阵,nh,l为回路数 目；hf为nh,p维 水 压 损 失 列 向 量；mh,N为nh,n维 热力源荷水流率列向量。式（21）可采用牛拉法进行求解。mh,N可以表示为:

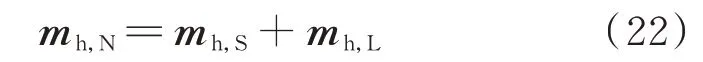
2.3.2 热力-㶲流模型

热力模型包括:热力源荷功率方程［19］、管道水温降落方程和节点水温混合方程,以描述热力管道和节点处的温度变化。热力源荷功率方程中,水传递热功率表示为温差、比热容与水流率的乘积,热力系统㶲流机理模型中提出,水传递热量㶲等于㶲势差与水流率的乘积［13］。如果热力系统非平衡节点㶲已知,将热力源荷功率方程中的供水和出口温度向量差与比热容的乘积cp(Ts-To)替换为供水和出口节点㶲势向量差ps-po,热力源荷功率向量Δϕ替换为热力源荷㶲向量Δeh,N,即替换为热力源荷㶲流方程,进而得到热力-㶲流模型,如式（23）所示。

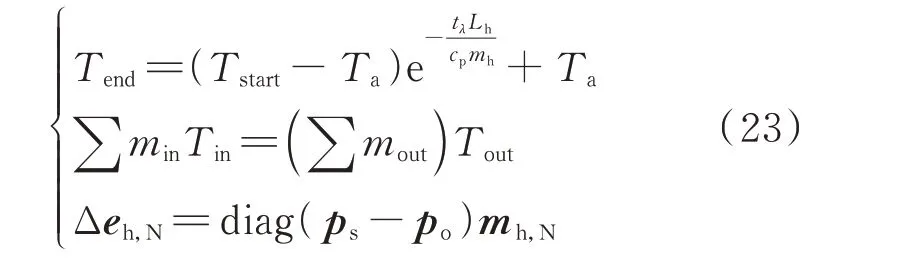
式 中:Tstart和Tend分 别 为 管 道 两 端 的 水 温；tλ为 热 传导系数；Lh为热力管道长度；Tin和Tout分别为流入和流出节点的水温；min和mout分别为流入和流出节点的水流率；Δeh,N为热力源荷㶲列向量,热源出口和回水节点㶲势相等,热源吸收和负荷放出热量㶲均可由上式热力源荷㶲流方程表示。

已知非平衡节点㶲,结合式（21）所示的水力模型和式（23）所示的热力-㶲流模型,可采用交替迭代［28］的方法求解热力系统㶲势和水流率,进而采用式（6）—式（14）求解㶲流分布,具体计算方法如附录B 所示。

2.4 㶲集线器模型

IES 分析中,常采用能源集线器模型对多能耦合环节即能源站进行建模,传统能源集线器可表示为［29］:

式中:Pin为nES,in维能源站输入功率列向量,nES,in为输入能量形式数目；Pout为nES,out维输出功率列向量,nES,out为输出能量形式数目；C为nES,out×nES,in能量耦合矩阵。

传统能源集线器从能量的角度建立能源站模型。考虑到不同能量存在“质”的差异,文献［30］提出了㶲集线器模型的概念,本文在此概念的基础上,基于功率流与㶲流之间的关系,建立了㶲集线器模型的通用化表达形式。文献［6,23］提到了基于能质系数的㶲计算方法,其中能质系数表示为单位能量所包含的㶲。能源站电、气或热端口㶲流e可表示为功率P与对应能质系数λ的乘积:

由式（1）、式（3）和式（5）可得,电力、天然气、热力端口的能质系数λe、λg、λh可分别表示为:

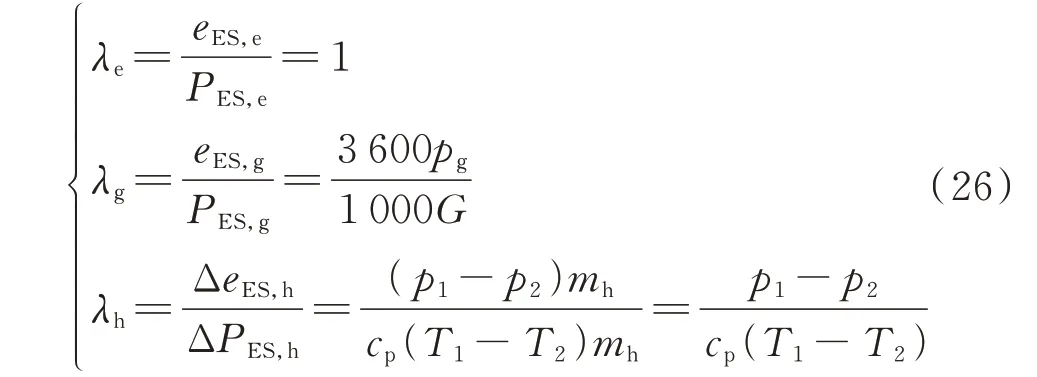
式中:PES,e、PES,g和ΔPES,h分别为能源站端口电、气和热功率；eES,e、eES,g和ΔeES,h分别为能源站端口电能㶲、燃料㶲和热量㶲；T1和T2分别为传递热量的热水两端的水温,p1和p2为两端对应的㶲势。

考虑规模化系统,以矩阵的形式表示式（25）,可将能源站输入和输出端口的㶲流表示为:

式中:ein为nES,in维输入端口㶲流列向量；eout为nES,out维输出端口㶲流列向量；λin为nES,in×nES,in输入和输出端口的能质系数矩阵；λout为nES,out×nES,out输入和输出端口各能量的能质系数构成的对角矩阵。电、气、热的能质系数均不为0。因此,λin和λout的对角线元素不为0,即λin和λout可逆。由式（24）和式（27）可得:

本文将式（30）定义为㶲集线器模型,将能源站等效为输入和输出端口有效能关系的接口,兼顾了能量的“量”和“质”。通过㶲集线器模型和输出端口㶲流,可获得输入端口的㶲流。附录C 选取两种典型能源站拓扑结构,展示了基于㶲集线器模型的能源站建模方法。

2.5 基于非平衡节点㶲的㶲流直接计算模型

在㶲流计算中,电力系统采用牛拉法求解系统㶲流；天然气系统采用牛顿节点法求解㶲流；热力系统采用水力模型和热力-㶲流模型交替迭代算法求解㶲流。三者基于㶲集线器模型耦合,耦合方式取决于系统的运行模式、设备类型等。本文选取“以热定电”的IES 运行模式展开分析,整体系统㶲流求解模型如图2 所示。具体流程如下:

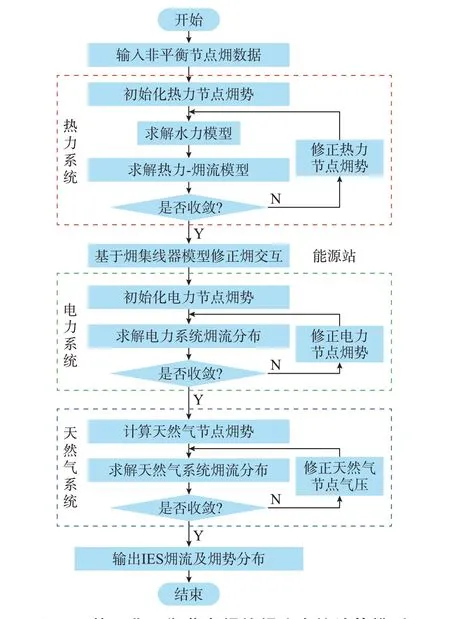
图2 基于非平衡节点㶲的㶲流直接计算模型Fig.2 Direct calculation model of exergy flow based on exergy of unbalanced nodes

1）获取IES 的负荷㶲,确定系统的运行方式、网架拓扑、能源站等信息；

2）设置热力节点㶲势初值,采用水力模型、热力-㶲流模型交替迭代的方法求解热力系统㶲流、㶲势分布；

3）基于㶲集线器模型,通过能源站输出的热量㶲,计算输入或输出的电能㶲、燃料㶲；

4）基于能源站输入或输出的电能㶲更新电力源荷㶲,设置电力节点㶲势初值,采用牛拉法求解电力系统㶲流、㶲势分布；

5）基于能源站输入或输出的燃料㶲更新天然气源荷㶲,计算天然气节点㶲势,采用牛顿节点法求解天然气系统㶲流分布；

6）获取IES 整体㶲流及㶲势分布。

2.6 㶲流直接计算模型和间接计算模型比较分析

基于非平衡节点功率的㶲流间接计算模型和基于非平衡节点㶲的㶲流直接计算模型均可获取IES㶲流及㶲势分布,但应用场景不同。㶲流间接计算模型适用于系统非平衡节点功率已知的情况,采用多能流计算获取能流、介质流率分布,进而计算系统节点㶲势,获得系统整体㶲流分布,再通过等效节点㶲流获取能源站㶲损情况。基于负荷㶲的㶲流直接计算模型适用于系统非平衡节点㶲已知的情况,构建各能源系统的㶲流计算模型,不需要先进行多能流计算,能源耦合环节即能源站采用㶲集线器模型进行建模。两种㶲流计算模型的对比分析如表1所示。

表1 两种㶲流计算模型比较Table 1 Comparison of two exergy flow calculation models

3 算例分析

3.1 算例介绍

基于已有多能系统算例,构建算例IES 如附录D 图D1 所示,系统管线参数如附录E 所示,中压天然气系统基于5 节点天然气系统［31］参数修改,气源气压为0.5 MPa,天然气理论燃烧温度为1 973 ℃,热值为45.75 MJ/m3［32］。热力系统基于8 节点热力系统［33］参数修改,系统由双热源供热,两个热源供水温度均为100 ℃,负荷出口温度为50 ℃。电力系统基于IEEE 33 节点配电网［34］参数修改,源端电压为12.66 kV。

此算例中采用两种典型能源站,便于分析不同能源耦合环节对IES 能源品质的局部影响。电力、天然气、热力系统通过能源站ES1 和ES2 耦合,ES1和ES2 结构以及与各能源系统的连接方式如附录D图D2 所示。其中,ES1 包含热电联产（combined heat and power,CHP）和燃气锅炉（gas boiler,GB）,CHP 气-电转换效率ηCHPg-e和气-热转换效率ηCHPg-h分别为0.3 和0.4,GB 气-热 转 换 效 率ηGBg-h为0.85,CHP 天然气分配系数v1为0.5［35］。ES1 采用“以热定电”方式运行,接入电力系统节点E6、天然气系统负荷节点G6、热力系统热源节点H1。ES2 包含电锅炉（electric boiler,EB）和GB,GB 气-热转换效率ηGBg-h为0.85,EB 电-热 转 换 效 率ηEBe-h为0.95［6］,ES2 中EB 和GB 产热相同,ES2 接入电力系统负荷节点E5、天然气系统负荷节点G7、热力系统热源节点H2。

附录F 展示了多能负荷功率已知场景。附录G表G1、表G2、表G3 是算例系统电流、气流、水流、电压、供水温度量测数据,结合节点㶲势的初始假设,用于估算多能负荷㶲数据,如表G4、表G5、表G6所示。

3.2 两种模型㶲流计算结果

基于本文提出的㶲流间接计算模型、直接计算模型,计算并分析典型运行场景下IES 的㶲流分布。

假设系统电、气、热负荷功率已知,分别如附录F 表F1、表F2、表F3 所 示,热 源 节 点H2产 热 为700 kW,基于㶲流间接计算模型,求解算例多能管线㶲流分布结果如表2 所示,源荷㶲、负荷㶲损结果如表3 所示,㶲流和㶲势分布结果如图3 所示。图中,绿色、蓝色、红色、紫色网络分别代表电力、天然气、供水、回水网络；图3（a）中的黑色、红色、紫色数字分别代表㶲流、㶲损、源荷㶲,单位kW；图3（b）中,电力系统的节点㶲势采用幅值（kV）和相角（rad）表示,天然气系统的节点㶲势均为8.88(kW∙h)/m3,热力系统节点㶲势的单位为kJ/kg。

假设系统电、气、热负荷㶲已知,分别如附录G表 G4、表 G5、表 G6 所 示,且H2供 应 㶲 为129.309 kW。基于㶲流直接计算模型,求解算例㶲流分布结果如表2 所示,源荷㶲、负荷㶲损结果如表3 所示,㶲流和㶲势分布与图3 结果一致。

传统基于能质系数的㶲计算方法可计算元件㶲损、传递㶲［6］。由表2 可知,基于功率损耗和能质系数可以求解多能管线㶲损；由表3 可知,基于源荷功率和能质系数可以求解源荷㶲,计算结果与本文间接和直接计算模型相同；基于本文模型采用式（26）同样可以计算源荷功率的能质系数,且计算结果与传统方法一致,以上结果验证了本文模型的正确性。

此外,表2、表3、图3（a）数据表明:㶲流在所有节点均满足局部㶲平衡关系,即流入节点的元件首端㶲流与源端供应㶲之和,等于流出节点的元件末端㶲流、负荷消耗㶲以及㶲损之和。由表2、表3、图3（a）可知,系统源端总供应㶲等于总负荷㶲与总㶲损之和,满足整体㶲平衡关系。因此,本文模型是合理的。

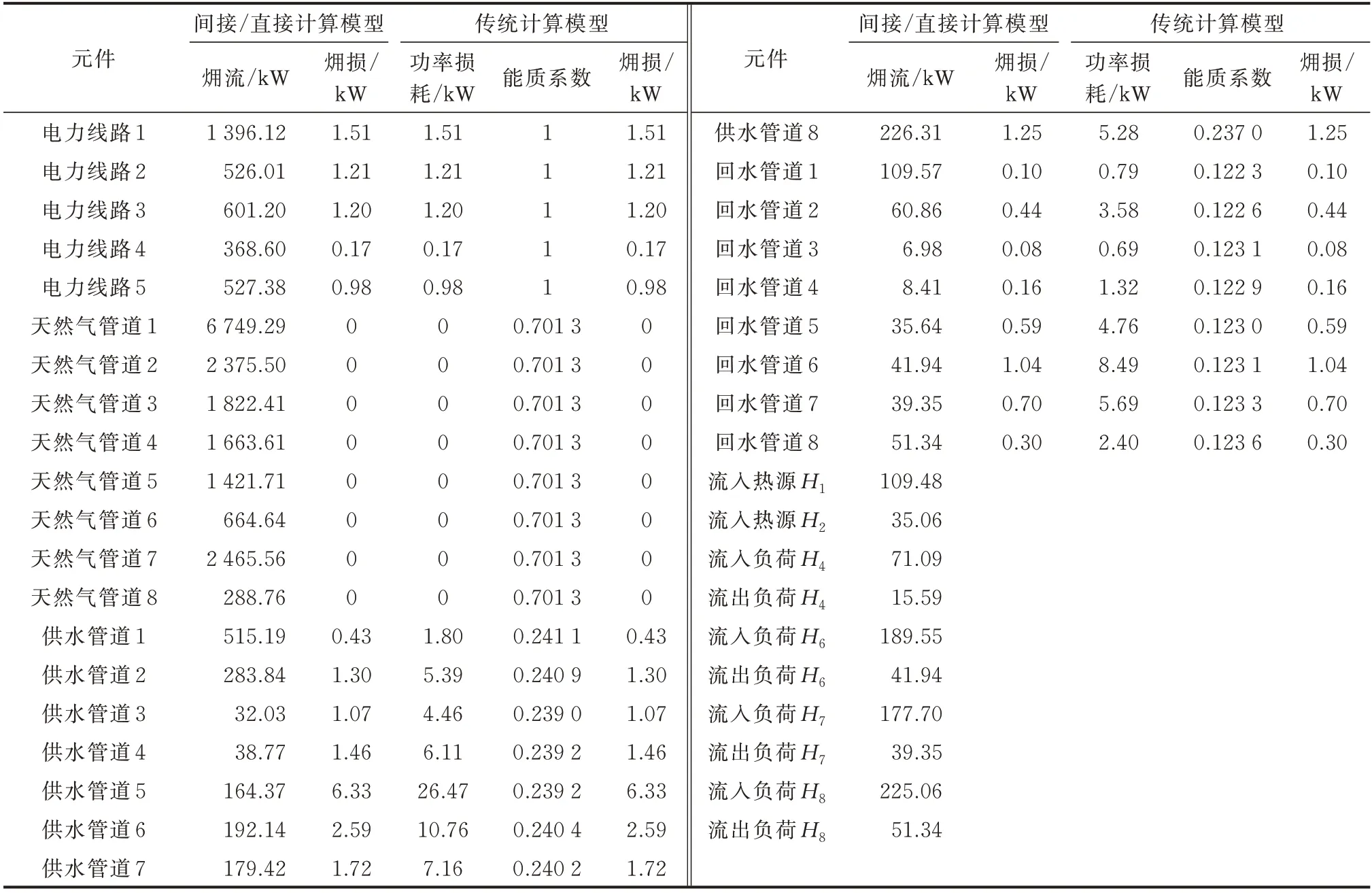
表2 多能管线㶲流分布计算结果对比Table 2 Comparison of calculation results of exergy flow distribution in multi-energy pipelines

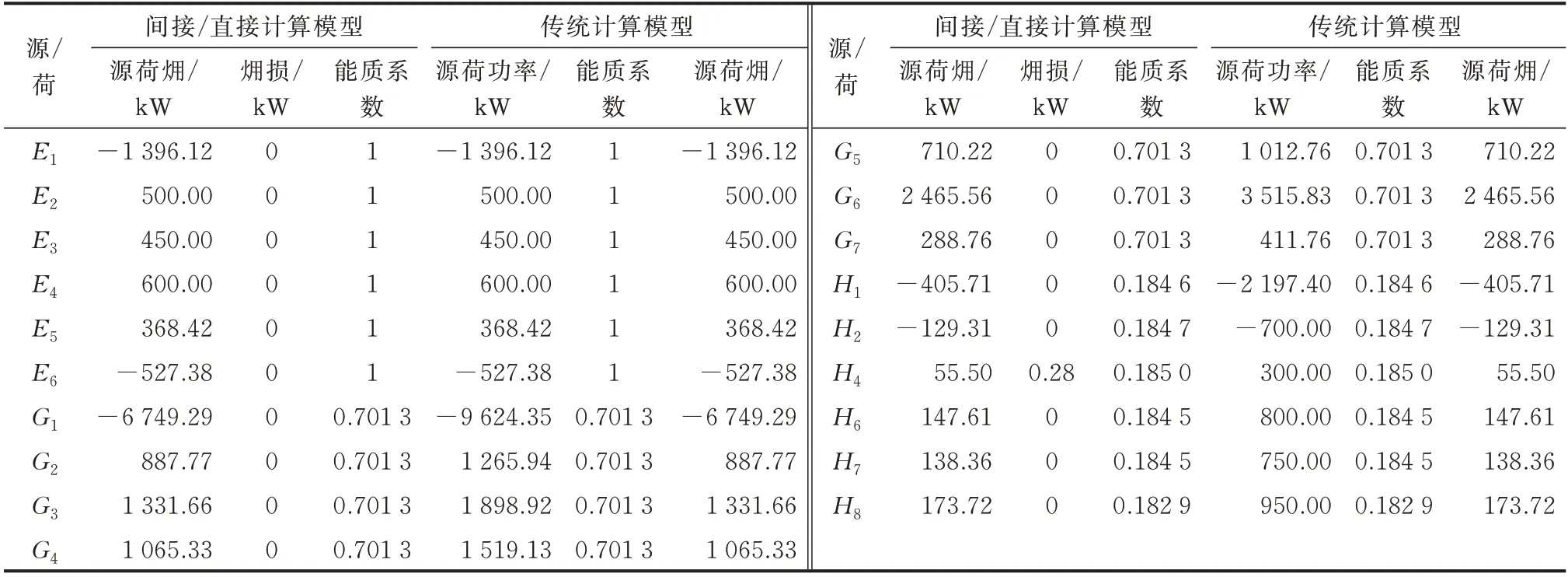
表3 源荷㶲和负荷㶲损计算结果对比Table 3 Comparison of calculation results of source and load exergy and load exergy loss

传统IES 㶲分析法缺乏对系统㶲流建模,由表2、图3（a）可知,本文模型不仅可求解㶲损、源荷㶲,还能计算网络中㶲流分布,实现整体和局部能源品质的协同分析,因此,本文模型与传统方法相比具有优势。对于已知非平衡节点功率的场景,传统方法首先需要计算能量和能质系数,然后计算㶲,以热力系统为例,不同元件传递的能量以及对应能质系数存在差异,不利于系统矩阵化建模。与传统方法相比,间接计算模型通过定义关联矩阵实现㶲流计算的矩阵化建模,使用更为简便,更适用于大规模IES的能源品质分析。对于已知非平衡节点㶲的场景,能流参数及能质系数无法直接获取,传统方法不再适用,而直接计算模型直接以㶲为研究对象,可以实现该场景下的系统㶲流计算。综上分析,本文模型与传统方法相比更具优越性。

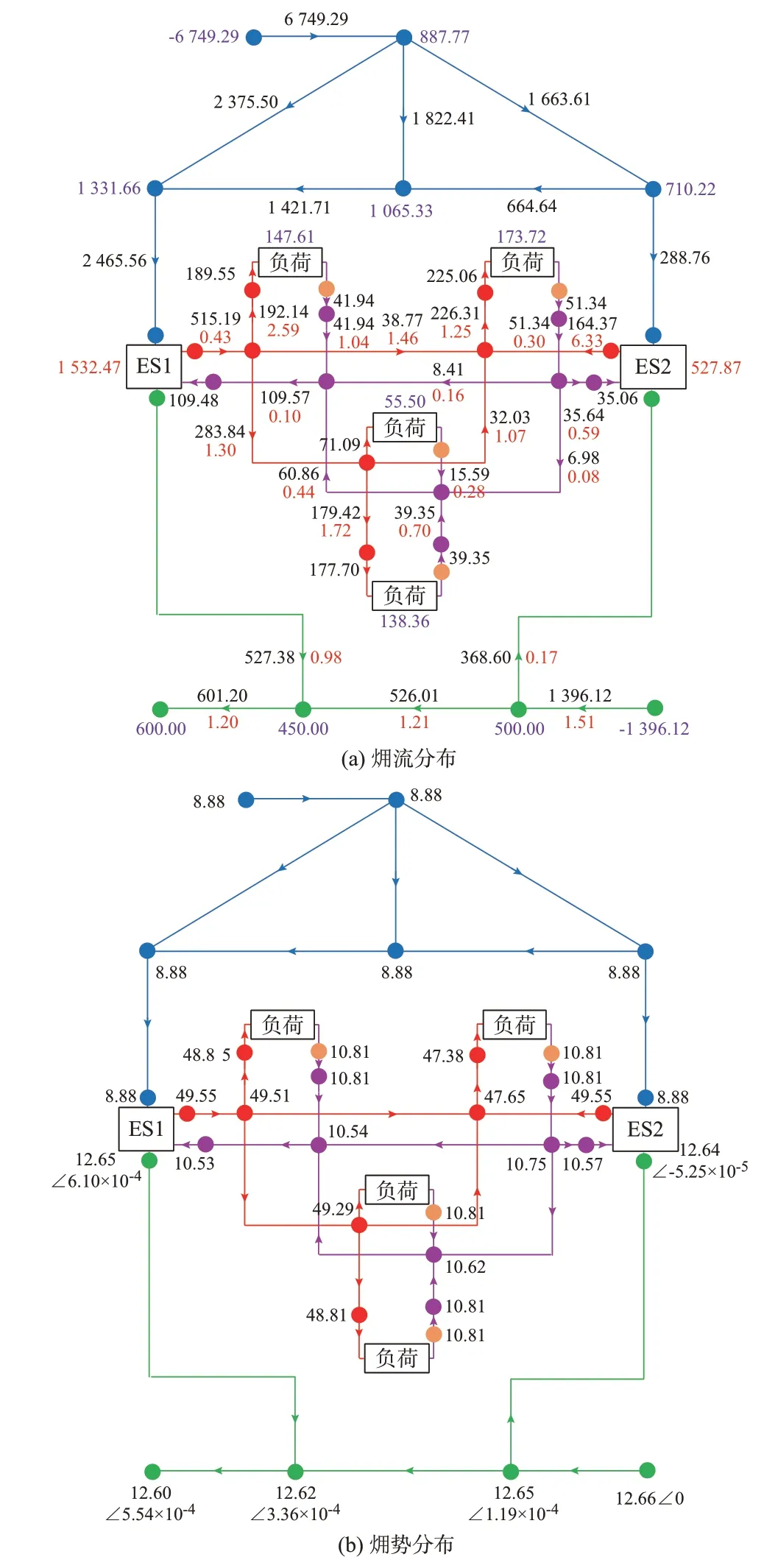
图3 算例系统㶲流和㶲势分布示意图Fig.3 Schematic diagram of exergy flow and exergypotential distribution of case system

3.3 两种模型中能源站耦合特性对比分析

㶲流直接计算模型中,采用㶲集线器建立能源站模型。根据ES1 和ES2 能源设备参数、运行参数、结构,由式（26）、式（29）、式（30）计算得到表征ES1 和ES2 当前运行状态的㶲集线器模型为:

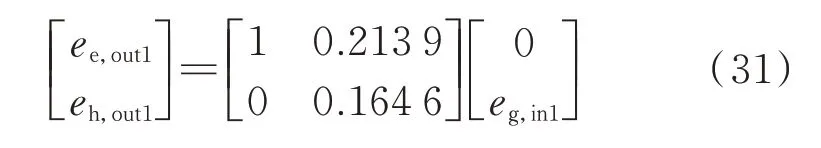
式中:eg,in1为ES1 输入端口的燃料㶲；ee,out1和eh,out1分别为ES1 输出端口的电能㶲和热量㶲；ee,in2和eg,in2分别为ES2 输入端口的电能㶲和燃料㶲；eh,out2为ES2 输出端口的热量㶲。

㶲流间接计算模型中,采用能源集线器建立能源站模型,得到表征ES1 和ES2 当前运行状态的能源集线器模型为:

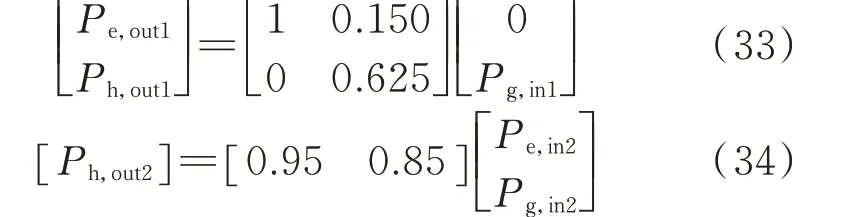
式中:Pg,in1为ES1 输入端口的气功率；Pe,out1和Ph,out1分别为ES1 输出端口的电功率和热功率；Pe,in2和Pg,in2分别为ES2 输入端口的电功率和气功率；Ph,out2为ES2 输出端口的热功率。

由式（31）—式（34）可知,能源集线器模型描述输入和输出端口能量关系,㶲集线器描述输入和输出端口有效能关系。根据ES1 输出端口的热量㶲可计算输入端口的燃料㶲和输出端口的电能㶲。已知GB 和EB 产热比例的条件下,根据ES2 输出端口的热量㶲可计算输入端口的电能㶲和燃料㶲,这恰恰体现了“以热定电”的运行模式特点。

分析式（31）、式（32）所描述的㶲耦合矩阵,以及式（33）、式（34）所描述的能量耦合矩阵,两种矩阵的维数、非零元素所在位置相同,但部分元素数值存在本质差异。㶲耦合矩阵中,部分元素对应高品质能量向低品质能量转化关系,其数值低于能量耦合矩阵中的对应元素。例如,ES2 将电能、天然气转换为低品质热量,式（32）所示的㶲耦合矩阵各个元素均小于式（34）所示的能量耦合矩阵对应元素。同理,㶲耦合矩阵中部分元素对应低品质能量向高品质能量转化关系,其数值高于能量耦合矩阵中的对应元素。例如,ES1 涉及天然气向高品质电能的转换,对应式（31）所示的㶲耦合矩阵的第1 行、第2 列元素0.213 9,高于式（33）中的对应元素0.150。当㶲耦合矩阵中的元素不涉及能量品质改变时,其数值与能量耦合矩阵中对应元素相等。综上,㶲耦合矩阵和能量耦合矩阵存在相似性和差异性,㶲耦合矩阵兼顾了能量的“量”和“质”。

能效、㶲效率作为能量和能质评估的重要指标,分别反映了能量和有效能的利用程度,本文定义能源站能效为能源站输出端口功率与输入端口功率的比值［36］,能源站㶲效率为能源站输出端口㶲与输入端口㶲的比值［37］。根据式（31）—式（34）计算ES1、ES2 的能效和㶲效率,得到ES1 能效为77.50%,ES2 能效为89.72%,ES1 㶲效率为37.84%,ES2 㶲效率为19.68%。由结果可知,ES1 能效低于ES2,但㶲效率高于ES2,说明ES2 中使用的EB 虽然拥有较高能效,但将大部分高品质电能转换为低品质热量,极大地降低了㶲效率,而ES1 中使用的CHP产生了高品质电能,有利于抑制能源品质的降低。由此可见,除了考虑经济性、能效等因素,能源站设备配置、运行优化、控制等研究还应全面考虑能源品质影响。

3.4 能源站产热量改变对能源品质的影响分析

考虑到外界负荷需求变化,ES1 或ES2 产热量由100 kW 变化为2 500 kW,算例系统的能源品质发生变化。

保持v1不变、ES2 中EB 和GB 产热相同,ES1和ES2 输入和输出功率的关系不受能源站产热改变的影响,由式（33）、式（34）表示,故ES1 和ES2 的能效恒为77.50%和89.72%。ES1 或ES2 产热量的改变影响了热力系统的运行方式,因此,对回水节点的水温和㶲势有影响。由式（26）可知,能源站输出热量的能质系数发生改变,结合式（31）、式（32）可知,ES1 和ES2 的㶲效率也发生改变。此外,热力系统运行方式的改变将影响网络中介质流率与节点㶲势的分布,进而改变系统㶲流分布。综上,系统中能源站产热量改变将影响各能源系统局部的能源品质情况。

以下进行量化分析,如附录H 图H1（a）所示,随着ES1 产热量增大,算例中能源站ES1 㶲损逐渐增大,ES2 㶲损逐渐减小,总的能源站㶲损占比较大,不同能源站的㶲损可能呈现相反的变化趋势,系统总㶲损呈现降低的趋势。如图H1（b）所示,随着ES2 产热量增大,ES1、ES2 㶲损以及系统总㶲损的变化趋势与ES1 产热量增大时的变化趋势恰好相反。

本文定义系统能效等于总负荷功率与源端供应总功率的比值［36］,系统㶲效率等于总负荷㶲与源端供应总能量㶲的比值［37］。由附录H 图H2（a）可知,随着ES1 产热量增大,系统能效呈现降低的趋势,而㶲效率变化趋势与能效相反,呈现逐渐升高的趋势。由图H2（b）可知,随着ES2 产热量增大,系统能效和㶲效率的变化趋势与ES1 产热量增大时的变化趋势恰好相反,ES2 中EB 能效较高,产热量增大时降低了系统能量损耗,在负荷不变的条件下,系统能效增大,算例拓扑较为简单,负荷㶲变化较小,随着系统㶲损的增大,系统的㶲效率逐渐降低。

由上述分析可知,实际IES 中的能源站运行方式、网络拓扑结构更为复杂,若综合考虑能源站、网络结构和运行方式的改变,系统能源品质特征将受更多因素的影响,各能源网络之间、能源站之间、整体与局部之间、能量与能质之间的关系更为复杂。基于㶲流分析与计算模型,可获取系统㶲流分布,进而按照需求采用非线性优化技术寻找优化方案,改善整体或某环节的能源品质情况,减少高品质能源损失。同时,能量和能质指标可能存在互斥性,IES规划、运行优化、控制等技术应该综合考虑整个系统、各能源站间、各能源网络间能量“量”与“质”的差异,考虑能量和品质的协同优化。

4 结语

本文基于IES 㶲流机理,提出了两种适用于不同场景的IES 㶲流计算模型。算例分析结果表明:

1）基于间接和直接计算模型,可有效求解IES㶲流、㶲势分布,前者针对已知非平衡节点功率的场景,后者针对已知非平衡节点㶲的场景,两种计算模型具有正确性、合理性、优越性。

2）两种计算方法采用的能源站模型存在差异,前者采用能源集线器模型,后者采用㶲集线器模型,㶲集线器模型中耦合矩阵反映了能源站输入和输出有效能之间的关系,兼顾了能量的“量”和“质”。

3）由两种计算方法结果可以看出,能源站能效高并不意味着㶲效率高,不同能源站出力配置对局部和整体的能源品质产生影响,后续规划、运行优化、交易、评估等技术研究中,需要综合考虑系统整体和局部之间的能源品质差异,兼顾能量“量”与“质”的差异,实现IES 能量的量质协同。

在后续的研究工作中,将考虑更多能源品质的影响因素,例如天然气或热力系统介质损失、管存、介质阻力、介质改变等因素对系统㶲流的影响,建立更为精细的IES 㶲流计算模型。基于㶲流计算模型,综合考虑系统整体和局部的能源品质差异,研究面向能源品质提升的IES 规划、运行优化、交易等技术。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。