基于双层模仿学习的多园区综合能源系统分布式协同优化调度

程 义，李更丰

（西安交通大学电气工程学院,陕西省西安市 710049）

0 引言

园区综合能源系统通过多能互补和多元储能提高能源利用效率,促进可再生能源消纳［1］,是应对能源环境危机的有效解决方案。园区间通过能量互济进行协同优化,可进一步降低总运行成本［2］。

多园区的协同优化分为集中式和分布式。集中式优化由决策者采集各园区数据及参数并求解全局优化问题。文献［3］通过电热互济建立多园区集中优化调度模型。但由于隐私保护问题,集中决策者实际难以获取各园区详细信息［4］。分布式优化将全局优化问题分解为多个子问题,由各主体单独求解。文献［5］采用交替方向乘子法（alternating direction method of multipliers,ADMM）实现多能源枢纽分布式协同优化运行。文献［6］建立了多园区非合作博弈优化模型。然而,以上研究均未考虑源荷多重不确定性。

文献［7］采用ADMM 保护各主体隐私,并在子区域内采用随机优化处理风电不确定性,随机优化需获得不确定量的准确概率分布,但实际难以获得。文献［8］将ADMM 和鲁棒优化相结合来解决电-气耦合综合能源系统分布式协同优化问题,但鲁棒优化仅制定应对最恶劣场景下的调度计划,与实际情况有较大偏差。

深度神经网络作为新一代人工智能技术核心,是一种通用拟合函数,能够以数据驱动方式拟合复杂不确定性概率分布,从而避免预测误差和建模不精确问题。

目前,已有较多研究将神经网络应用于电力系统不确定性调度问题。文献［9-11］采用深度Q 网络（deep Q network,DQN）分别对微网、储能和电动汽车进行动态优化调度。文献［12-13］采用深度确定策略梯度（deep deterministic policy gradient,DDPG）对园区综合能源系统和含风电系统进行不确定性优化调度。文献［14］采用多智能体深度确定策略梯度（multi-agent deep deterministic policy gradient,MADDPG）实现多园区系统的分布式协同优化运行。文献［15］以通信神经网络（communication neural net,CommNet）作为智能代理,采用近端策略优化（proximal policy optimization,PPO）进行训练,实现主动配电网分布式电源优化调度。

以上研究均采用强化学习训练神经网络。但是,强化学习不属于监督式学习,其训练数据非平稳分布,收敛性差,对大量超参数敏感。

模仿学习则是策略神经网络的监督式算法,具有良好的收敛稳定性和全局最优性。文献［16］采用模仿学习实现了发电商参与电力市场的智能决策。

针对多园区综合能源系统协同优化过程中的不确定性和隐私保护问题,本文提出一种双层优化模型［17］。上层采用通信神经网络来兼顾不确定性和隐私保护问题,实现对储能设备的预测决策一体化调度；下层采用ADMM 进行分布式优化得到完整的多园区协同调度方案,并通过算例验证了所提方法的有效性。

1 多园区综合能源系统协同优化调度建模

1.1 多园区综合能源系统结构

本文研究的多园区综合能源系统的整体结构如图1 所示。

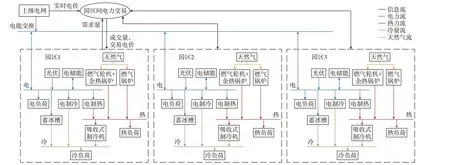
图1 多园区综合能源系统结构示意图Fig.1 Schematic diagram of structure of multi-park integrated energy system

每个园区均为冷热电联供型综合能源系统,包含光伏、热电联产、燃气锅炉、电制热、电制冷、电储能和蓄冰槽等常见单元［18］。

各园区通过电力互济形成多园区协同系统,同时也可以向上级电网购电。

1.2 集中式优化调度模型

多园区综合能源系统的集中式优化目标为总体运行成本最低,将各个园区的购气、向上级电网购电和储能运行折旧成本相加即得到总运行成本最小化目标函数,如式（1）所示。

多园区协同优化问题的约束条件包括所有园区的约束条件,每个园区又包括功率平衡约束和各类设备运行约束。

1）功率平衡约束

各园区均需满足电、热、冷功率平衡约束:

2）设备运行约束

热电联产以定热电比模式运行,并满足功率限值约束:

燃气锅炉、电锅炉、电制冷和吸收式制冷机均为能量转化模型,并满足功率限值约束:

蓄冰槽利用蓄冷介质进行储冷,处于蓄冷工况时,其消耗电功率以增加蓄冷量；处于制冷工况时,其不消耗电功率,通过热交换形式进行融冰释放冷量,满足冷负荷需求。模型如下:

电储能模型与蓄冰槽类似。为保持电储能持续稳定运行,要求在一个调度周期始末电储能的储量相等。电储能模型［19］如下:

1.3 园区间电力交易机制

1.3.1 交易电价机制

园区间交易电价在上级电网的售电与购电实时电价之间,才能使购电园区以低于向上级电网购电电价从其他园区优先购电,以节约购电成本,并使售电园区以高于向上级电网售电电价向其他园区优先售电,以增加售电收益,即

具体的交易电价应能够反映实时的上级电网电价和多园区系统的供需情况。当供大于求时,处于买方市场,价格应偏向买方利益,即价格较低,购电成本低；而供小于求时,处于卖方市场,价格应更加利于卖方,即价格较高,售电收益高。因此,设计如下的园区间交易电价决定机制,将上级电网实时购售电价以多园区系统总供求量为权重进行加权平均,得到园区间实时交易电价,即

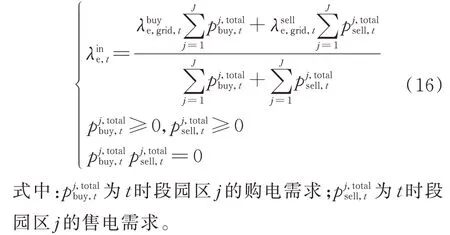
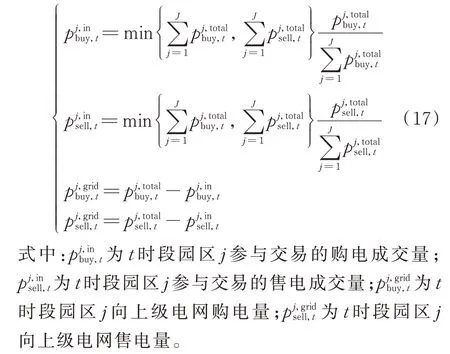
1.3.2 交易量分配机制

当供需总量不平衡时,应按照各园区的供需量比例来分配交易量,未满足的需求则由上级电网平衡:

2 通信神经网络及模仿学习原理

2.1 通信神经网络

通信神经网络对各智能体神经网络输入的隐私数据编码后在隐层进行信息交互,其示意图和通信机制说明如附录A 图A1 和式（A1）所示。

2.2 模仿学习

2.2.1 行为克隆

模仿学习是一种使神经网络效仿专家行为的训练方式。

行为克隆是最直观的模仿学习方式。神经网络以状态作为输入数据,以专家动作作为标签,进行监督式训练,形成由状态到动作的策略映射。行为克隆的示意图及局限性说明如附录A 图A2 所示。

2.2.2 数据增强

数据增强（dataset aggregation,DAgger）算法则是一种改进的模仿学习,能够有效解决有限范例样本以及累积偏离误差的问题,如附录A 图A3 所示。

3 基于通信神经网络和ADMM 的多园区综合能源系统分布式协同优化调度

在多园区系统中,各园区储能设备的实时调度存在不确定性和隐私保护两个问题。不确定性问题在于储能实时调度需要预测源荷及电价等不确定因素在未来时段的走势,以预留合理的储量空间；隐私保护问题在于各园区储能全局最优调度需要获取互联的其他园区信息。

为兼顾储能实时调度所面临的不确定性和隐私保护问题,在本文建立的双层优化模型中,上层采用多智能体通信神经网络来决策各园区储能动作。经模仿学习训练,智能体可获得预测决策一体化功能,并通过独特的隐层加密通信结构,保护了各园区数据隐私。其余设备动作不影响未来时段的系统能量状态,属于单时段确定性优化问题。

同样,为了保护各园区隐私,本文在模型下层采用ADMM 对问题进行分布式求解,各园区间只需交互少量耦合变量信息,各自求解优化子问题并进行迭代即可获得与集中式优化一致的最优解。

3.1 上层采用多智能体通信神经网络

3.1.1 状态空间

各园区智能代理的输入状态空间为局部实时状态信息,包括当前调度时段该园区的光伏、电热冷负荷、向上级电网购电的实时电价（这里假设不存在向上级电网售电或售电电价为零）、电储能和蓄冰槽的储量状态,即

3.1.2 动作空间

各园区智能代理的输出动作空间为当前时段的储能设备动作（根据下一时段的储量状态可计算出当前时段储能设备充放功率）,即

3.1.3 动作可行域

用于决策的神经网络在输出动作时,经非线性函数Sigmoid 处理后,将输出值限制在［0,1］区间内,输出值的意义为下一时段的储量状态。然而,储量状态需要满足多种约束条件,因此,在将神经网络输出值转换为设备实际动作时,需要求出当前时段的动作可行域［20-21］,以保证满足相关约束条件。每一时段动作可行域的求解过程如附录A 式（A2）—式（A5）所示。

3.1.4 模仿学习专家策略

利用源荷及电价的历史数据构造完美预测信息下的集中式优化模型作为模仿学习的专家策略,来提供每一时段的最优储能动作作为标签,其优化时域为当前时段到调度周期结束的全部后续时段,即

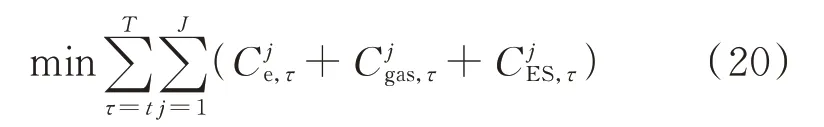
式中变量含义见式（1）,其中每个时段的各园区约束条件见式（2）—式（14）。

3.2 下层采用ADMM

每一时段,由模型上层确定了储能设备动作后,多园区系统的其余设备动作则由模型下层采用ADMM 对单时段确定性优化问题进行分布式求解［22］。具体求解过程如附录A 式（A6）—式（A9）所示。

3.3 园区间电力交易

通过ADMM 求出的某园区与上级电网以及与其他园区的交互电功率之和,即为该园区的购、售电需求,如式（21）所示。

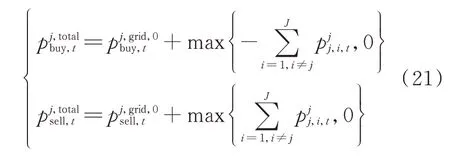
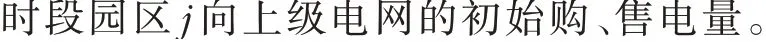
然后,将各园区的总购、售电需求输入1.3 节所述的电力交易机制中,即可确定当前时段的交易电价和各园区交易成交量以及向上级电网的最终购、售电量。

3.4 双层优化架构

将多智能体通信神经网络增强模仿学习和ADMM 相结合,并通过所提电力交易机制进行园区间合理利益分配的双层分布式优化架构,如图2所示。

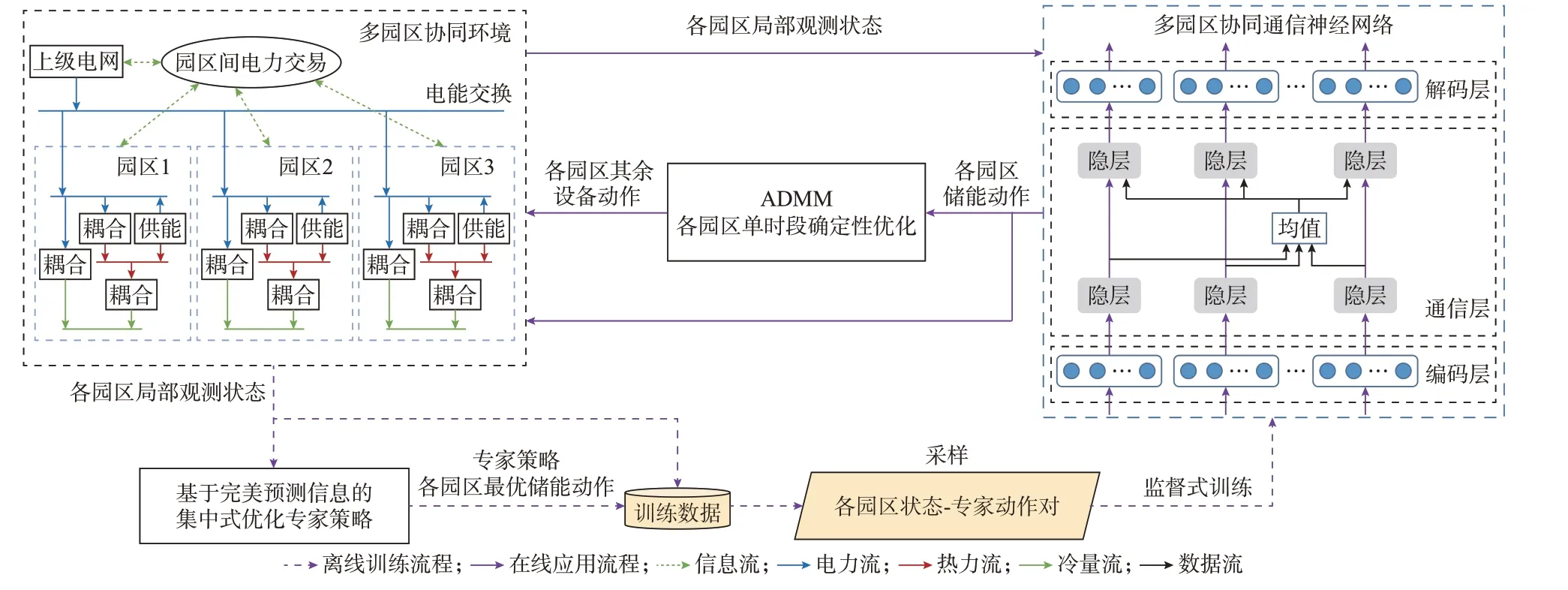
图2 基于通信神经网络和ADMM 的多园区双层优化模型Fig.2 Multi-park bilayer optimization model based on CommNet and ADMM

4 算例分析

为验证所提双层优化模型的有效性,采用3 个园区构成的多园区综合能源系统作为算例进行仿真研究。以一天24 h 为一个调度周期,1 h 为一个调度时段。每个园区中的设备参数及成本参数如附录B表B1 所示。

4.1 场景对比

为验证多园区电力互济协同优化的经济优势,设置各园区独立优化和多园区协同优化两个场景。

算法1:完美预测信息下的多园区系统集中式优化,即理论最优策略。

算法2:本文所提的基于通信神经网络和ADMM 的双层优化模型。

算法3:各园区独立运行,并基于各自的完美预测信息进行优化调度。

算法4:各园区独立运行,无预测信息,不考虑储能系统,每一调度时段仅对园区中其他设备依据即时信息进行单时段优化的贪婪优化策略,即理论最劣策略。

通信神经网络训练所需的样本数据由各园区光伏、电热冷负荷及实时电价的典型日基准曲线叠加截断正态分布随机量抽样得到。各园区典型场景如附录B 图B1 所示,其中园区2 的样本数据如附录B图B2 所示,园区1 和园区3 按同样方法进行场景生成。

本文算法采用的通信神经网络包含3 个隐层,分别为编码层、通信层和解码层,3 个隐层神经元数量均为64,隐层采用的激活函数为ReLU,输出层采用的非线性函数为Sigmoid,经验池大小为1 000,每次训练采样批量大小为128,学习率为0.000 1。

在训练过程中所得总运行成本收敛曲线如图3所示。智能体经过约1 000 个训练周期后基本收敛,能够逼近完美预测信息下的集中式优化方法。神经网络的均方差损失函数在训练过程中逐渐减小,如附录B 图B3 所示。

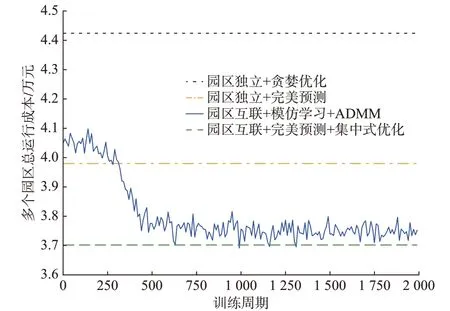
图3 训练过程中所有园区的总运行成本Fig.3 Total operation cost of all parks during training process

由不同算法调度所得各园区典型日运行成本以及所有园区总运行成本统计结果如表1 所示。

表1 不同场景的日运行成本Table 1 Daily operation costs in different scenarios

对比各园区独立运行和多园区电力互联两种场景下的理论最优策略,证明各园区间的电力互济能够使资源在更大范围内优化配置,利于降低总体运行成本。

观察4 种算法所得总运行成本,可见算法2、算法3 和算法4 比算法1（理论最优策略）的调度成本分别升高了1.16%、7.50%和19.51%,并且其中独立运行和协同运行两种场景的理论最优策略（算法3 和算法1）需要对整个调度周期的源荷及实时电价等不确定因素进行完美预测,实际无法达到。这说明,本文所提双层优化模型能够实现多重不确定性环境下多园区系统的分布式协同优化运行,在保护各园区数据隐私的前提下,不需要预测值,只根据即时信息即可实时决策,并获得与理论最优策略接近的性能。

4.2 不确定性算法对比

为验证所提算法在处理不确定性问题方面的优势,采用同为神经网络智能算法的MADDPG 算法和基于预测值进行滚动优化的模型预测控制（model predictive control,MPC）算法进行对比。智能算法的训练过程如附录B 图B4 所示,3 种算法产生的总运行成本统计数据如表2 所示。

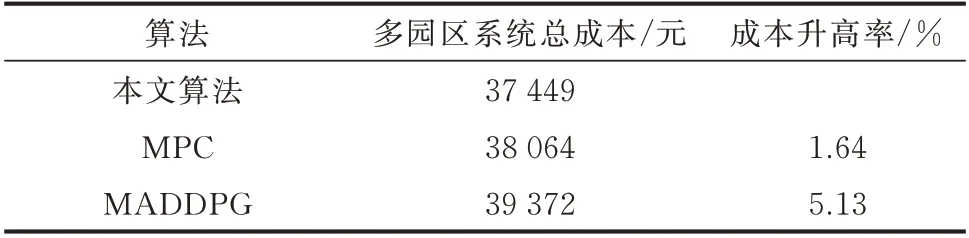
表2 不同算法的调度成本Table 2 Dispatch costs of different algorithms

由于源荷和电价的不确定性,MPC 方法会受到预测误差较大影响；而MADDPG 强化学习方法则是算法本身难以收敛到全局最优点。可见,本文所提方法在不确定性优化调度问题上,相比于MPC 方法和MADDPG 强化学习方法,能够避免预测误差带来的影响,具有较好的全局最优收敛性,并获得最优调度结果。

通过3 种算法及理论最优策略进行调度所得到的储能设备储量状态曲线分别如附录B 图B5、图B6 和图B7 所示。可见,本文算法通过模仿完美预测信息下的集中式优化专家策略,调度得到的储量状态变化曲线在变化趋势与数值上均能逼近最优储量状态变化曲线,能够依据源荷与电价的变化趋势合理协调储能系统的充放能行为。

4.3 ADMM 分布式算法分析

为验证本文模型下层采用ADMM 分布式求解单时段确定性优化问题的有效性,采用集中式优化方法和ADMM 分布式方法分别求解模型下层问题进行对比。其中,ADMM 中的耦合变量和拉格朗日乘子的初值均取0,惩罚系数和残差收敛阈值均取0.01。两者求解结果如附录B 表B2 所示。

可见,采用ADMM 分布式算法与集中式优化方法求解出的结果完全一致,而且分布式算法具有保护各主体隐私的优势。

图4（a）统计了一个调度周期中每个调度时段ADMM 分布式算法的迭代次数,图4（b）以16:00—17:00 的调度时段为例,展示了迭代收敛过程中原始残差和对偶残差的数值变化。

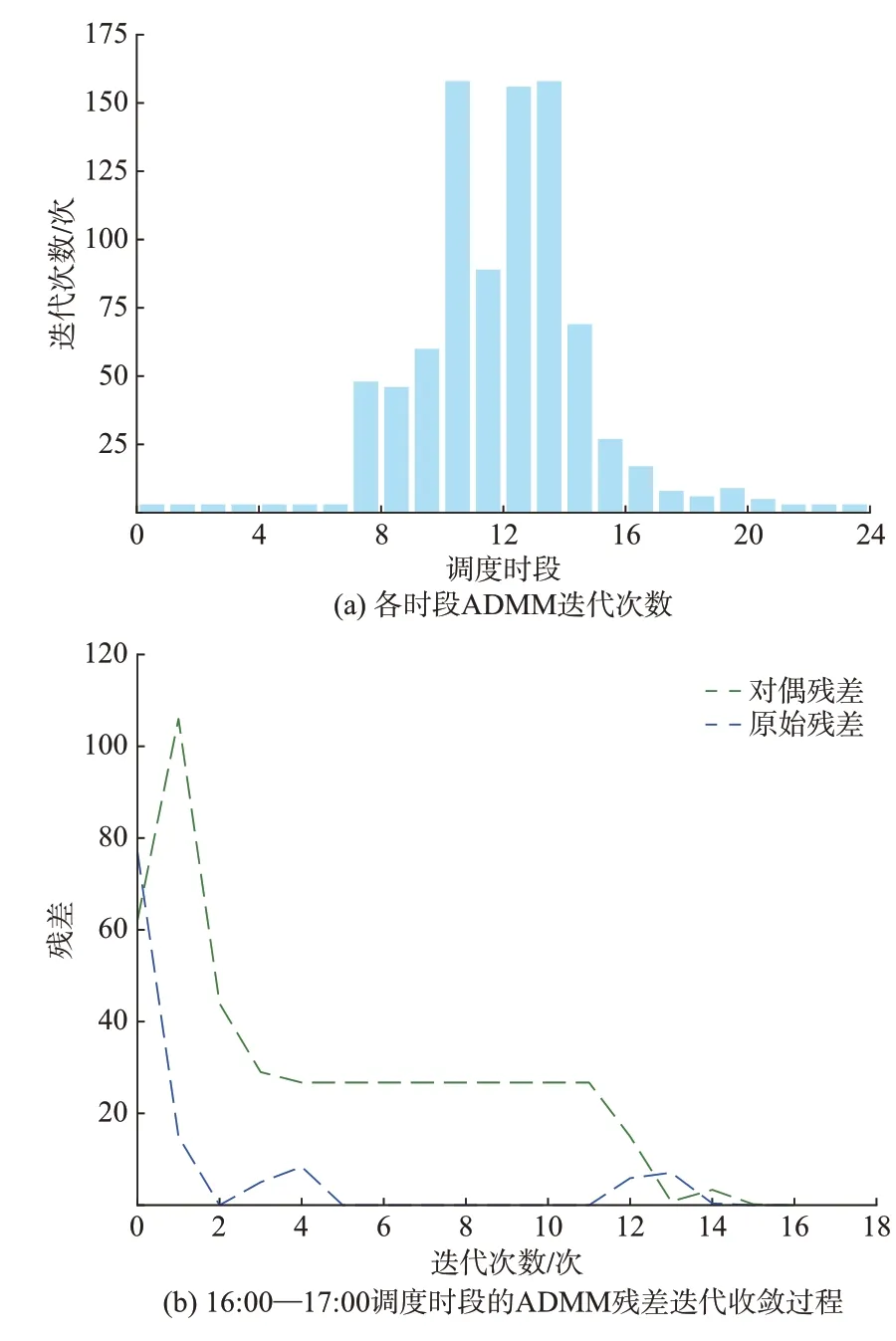
图4 ADMM 的迭代过程Fig.4 Iteration process of ADMM

可见,随着迭代进行,原始残差和对偶残差虽有波动,但总体趋势均稳步下降直至小于设定阈值,所有时段优化问题的ADMM 分布式求解过程均具有较好的收敛性。

4.4 园区间电力交易机制有效性分析

由本文所提园区间电力交易机制所确定的交易电价、交易电量和各园区向上级电网购电量如图5所示。

由图5 可知,各园区主要在外部电价较低时段向上级电网购电以满足需求,而在外部电价较高时段进行园区间电力交易。本文所提交易电价机制形成的交易电价比上级电网电价约降低了一半的水平。

各园区运行成本构成如表3 所示。园区1 光伏出力大于负荷需求,作为主要售电方,将多余电量卖给其他园区,获得售电收益；而园区3 的光伏出力小、负荷水平高,作为主要购电方,以低于上级电网购电价格的交易电价来购买其他园区的电力,减少购电成本。购售双方均能从园区间电力交易中获益。

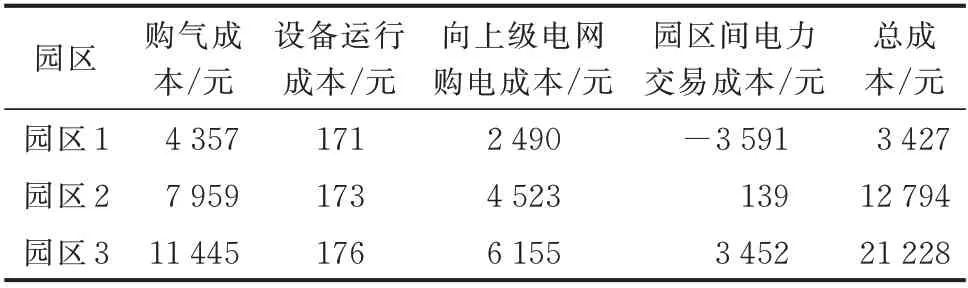
表3 各园区成本构成Table 3 Cost composition of each park

为进一步验证本文所提交易量分配机制的合理性,以时段18～19 为例,该时段采用ADMM 求出的初始交易结果和经交易机制处理得到的最终交易结果对比如表4 所示。

由图5 和表4 可知,在时段18～19,供小于求,处于卖方市场,由所提交易电价机制确定的实时交易电价相对较高,为0.63 元/（kW·h）,比较接近该时段向上级电网购电的电价0.79 元/（kW·h）,反映了实时供求关系。

表4 各园区交易电量分配Table 4 Distribution of transacted electricity quantity in each park

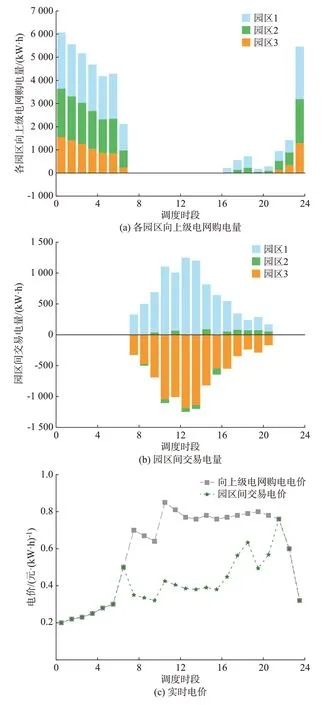
图5 多园区综合能源系统电力交互结果Fig.5 Power interaction results of multi-park integrated energy system

该时段有两个购电方即园区2 和园区3,由ADMM 求出的初始交易结果是两园区等分交易量,即均向园区1 购买119 kW·h 的电量。但是,园区3本身有远大于园区2 的购电需求,其剩余大量的购电需求需要向上级电网购买,两园区间的交易量分配和成本分摊并不合理。经本文所提交易量分配机制处理后,两园区按总购电需求比例来分配交易量份额,从而保障了各园区的合理利益。

4.5 优化结果分析

园区1 的典型日调度结果如附录B 图B8 所示。在外部电价较低时段0～6,向上级电网购电满足电负荷,通过电制热和电制冷满足热、冷负荷,并分别向电储能和蓄冰槽充电和蓄冰；在光伏大发时段7～17,将过剩光伏电量通过电力交易卖给其他园区,热负荷则利用燃气锅炉供应；在光伏出力减小而外部电价仍较高的时段17～23,同时存在热负荷与电负荷,故采用热电联产同时供热供电是最经济的供能方式,并且电储能和蓄冰槽释放能量以满足电、冷负荷需求。

园区2 的典型日调度结果如附录B 图B9 所示。园区2 自身的供需水平较为匹配,故在园区间电力交易中的参与程度较低。园区3 的典型日调度结果如附录B 图B10 所示。园区3 的光伏出力小而负荷水平较高,因此,在上级电网购电价格较高时,以较低的交易电价购买其他园区电量,节约购电成本。

5 结语

针对多园区综合能源系统协同优化运行过程中面临的隐私保护问题和多重不确定性因素,本文将通信神经网络增强模仿学习和ADMM 结合,建立了适用于多园区系统分布式协同的双层优化模型,并提出了相应的园区间交易机制以保障各园区利益。通过算例验证了所提方法不依赖于对源荷及电价等不确定量的准确预测,能够在保护各园区数据隐私的前提下,达到与基于完美预测信息的集中式优化方法接近的性能,并验证了所提交易机制的合理性。

本文对系统不确定性因素的仿真建模较为简单,后续研究考虑利用真实历史数据,在更大规模算例上验证模型的有效性。此外,本文以集中式优化作为专家策略,后续研究重点在于进一步考虑各园区间的博弈均衡,对多园区系统进行更加合理的利益分配。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。