弱电网中锁相环型并网变换器非线性暂态稳定解析分析

熊佳旺，孔 力，叶 华，裴 玮，韩一江

（1. 中国科学院电工研究所,北京市 100190；2. 中国科学院大学电子电气与通信工程学院,北京市 100049）

0 引言

随着中国“双碳”战略目标的实施,以光伏、风电等新能源为主体的新型电力系统得到迅速发展。同时,电力电子变换器以其灵活控制、促进新能源消纳水平等优势在新型电力系统中得到广泛应用［1-2］。然而,与传统同步发电机相比,电力电子变换器具有惯量小、动态过程快且复杂等特点,这给新型电力系统的暂态分析带来严峻挑战［3］。美国南加利福尼亚900 MW 光伏失稳［4］、2019 年英国大停电［5］、中国新疆哈密风电场的次同步谐振［6］等实际案例表明,对并网变换器系统进行暂态分析是必要的。

并网变换器通过锁相环（phase-locked loop,PLL）采集公共连接点（point of common coupling,PCC）的电压并对其进行控制,以维持变换器与交流电网的同步运行。一方面,PLL 的非线性特性使并网变换器与电网间的稳定分析变得更为复杂；另一方面,高比例新能源的接入使外部电网强度降低,呈现出弱电网的特性。因此,亟须开展弱电网环境下并网变换器的稳定性分析。

针对并网变换器的稳定性分析,国内外开展了大量小信号稳定性研究［7-11］,如特征根分析、阻抗分析等。研究结果表明,含PLL 的并网变换器在弱电网系统中具有负阻尼性质,且基于dq坐标变换的PLL 控制器设计可能会导致系统产生共振而失稳［7-8］。小信号模型主要将系统模型线性化以达到可运用线性控制理论分析的目的［9-11］。然而,该简化过程在小扰动场景下较为精准,但针对大扰动场景,该方法误差较大,无法描述系统非线性特性,难以获得精准的稳定判据。

与小信号方法相比,暂态分析方法更适合研究非线性特性。最早的暂态稳定研究主要通过电磁暂态程序的仿真结果［12］进行分析,虽然该方法可以模拟各种暂态现象,但大规模系统的仿真运算时间长、效率低,难以获得数值稳定边界。等面积法［13］大量运用于传统同步发电机的暂态分析,并且在其他系统的稳定性分析中得到了应用与拓展。文献［14］提出了不同电网故障强度的电压源型变换器等面积分析方法,然而在分析过程中忽略了系统阻尼。文献［15］对等面积方法进行修正并分析,但并未定量分析系统的稳定边界。李雅普诺夫函数法［16-19］作为非线性系统中常用的分析方法,常用于电力系统暂态分析,如能量函数法［18-19］。该方法通过构造李雅普诺夫函数得出稳定判据,但过于保守,且难以找到通用的构造方法。尽管以上方法在系统暂态稳定分析中得到了一定运用,但无法提供解析式来描述并网变换器系统的暂态稳定性,难以获得简洁实用的稳定判据。

围绕上述问题,本文推导了基于系统扰动量的非线性动力学模型,通过平均法计算了系统扰动量的近似解析解,获得了系统的稳定边界,并分析了系统非线性项及系统参数对稳定性的影响。本文首先阐述了系统典型结构及所建立的非线性动力学模型；然后,计算并获得系统稳定判据；最后,分析关键参数对系统稳定性的影响并进行仿真与实验验证。

1 弱电网连接的并网变换器

1.1 系统描述

本文研究弱电网连接的并网变换器暂态稳定性,将电网侧等效为带阻抗的无穷大电源,变换器通过PCC 与弱电网相连。图1 为系统的简化模型。其 中:Vg、VPCC、Vc、θg、θPCC、θc分 别 为 电 网 相 电 压、PCC 电压、并网变换器输出端口电压幅值及其对应相角；Isabc为系统线路三相电流值；Zg和Ls分别为电网侧等效阻抗和滤波电感；Lsd和Lsq分别为Ls的d、q轴分量；Vdc和Cdc分别为变换器直流侧电压及其滤波电容；ωn为固有角频率,其值为100π；θPLL为PLL的 输 出 相 角；Isd、Isq、Isd,ref、Isq,ref分 别 为 并 网 变 换 器 电流环电流Is的d、q轴分量及其参考值；ud和uq分别为PCC 电压的d、q轴分量；mabc、md、mq分别为控制器的输出信号及其d、q轴分量；PI 表示比例-积分环节。

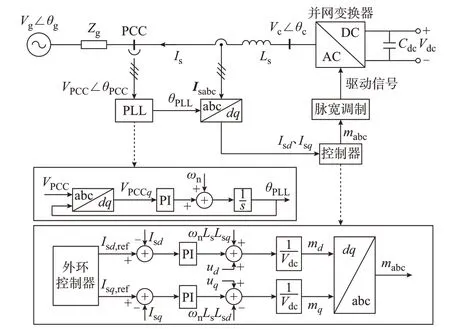
图1 弱电网连接的并网变换器简化模型Fig.1 Simplified model of grid-connected converter connected to weak grid

为获得系统的二阶动力学模型,本文做出如下假设:

1）考虑到PLL 的带宽通常为2～20 Hz,而电流环的带宽通常为20～100 Hz［20］,因此,本文将电流环解耦分析,并直接给定电流参考值,即Isd=Isd,ref、Isq=Isq,ref。

2）本文模型存在一个平衡点,因为若系统不存在平衡点,必然失稳［21］。

3）线路阻抗通常表现为电阻和电感的形式,线路电阻通常表征为阻尼特征,对系统的稳定性起到积极的作用,因此,本文分析纯电感线路来描述系统最极端的场景,即Zg=Lg,其中Lg为电网侧等效电感。

1.2 基于系统扰动量的非线性动力学模型

基于本文做出的假设,系统PCC 处的q轴电压Vpccq为:

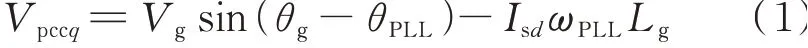
式中:ωPLL为PLL 的输出角速度。

根据图1 可以得到并网变换器的PLL 数学微分模型为:

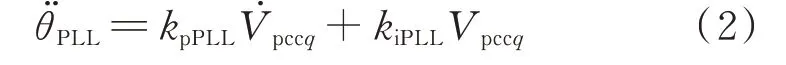
式中:kpPLL和kiPLL分别为PLL 控制器的比例、积分系数。

为建立系统的动力学模型,本文定义PLL 输出角度与电网侧角度差δ为:

式（4）中,M>0 是保证ωn1为实数的前提。然而当并网变换器向电网侧进行供电时,M可能为负数。此时,可对式（4）中的角度差做δ=-δ变换,便可保证ωn1为实数,且变换前后方程形式不变,因此式（4）所表达的系统二阶非线性动力学模型具有普适性。

文献［22］指出,任意系统的振荡可分为稳态量和扰动量,其中稳态量主要影响系统静态工作特性,扰动量主要影响系统动态工作特性。因此,本文将系统振荡分为稳态量δ0和扰动量δd,即δ=δ0+δd。将其代入式（4）并整理可得:

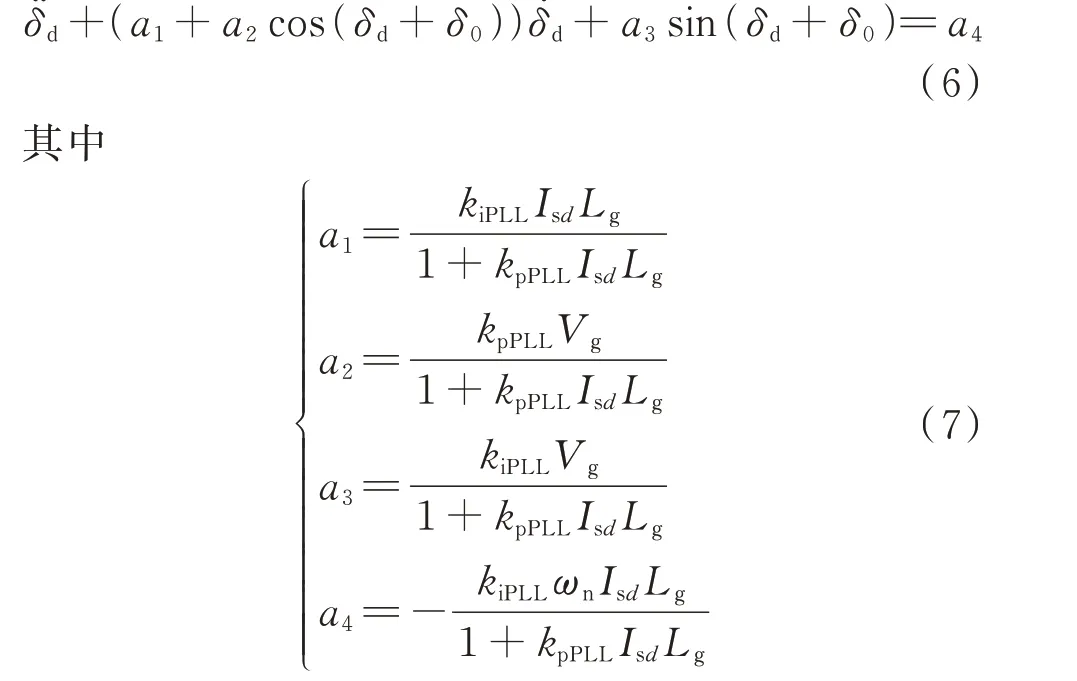
进一步地,本文将稳态量设为平衡点,即稳态量可表示为:

因此,基于系统扰动量的非线性动力学模型可以表示为:

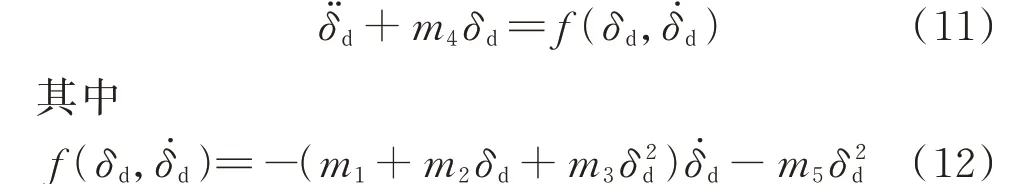
2 基于平均法的稳定判据

为研究弱电网环境下并网变换器的暂态过程,需要一种时域分析法来预测系统运行轨迹及稳定边界。本文提出的基于系统扰动量的非线性动力学模型与非线性振动理论中的振动方程有诸多相似之处,例如达芬方程、范德波尔方程等。本文借鉴单自由度自治系统的平均法［23］对非线性动力学方程进行求解,进而获得其稳定判据。

2.1 平均法

平均法适用于分析精度仅限于基频分量的非线性系统,系统模型的表达式为:

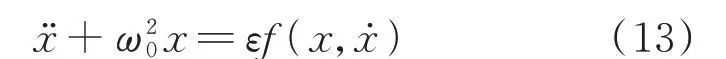
式中:x为变量；ω0为系统角频率；εf(x,ẋ)为非线性项,其中ε为足够小且与x、ẋ无关的独立参数。

式（13）等号右侧项为系统的非线性项,当ε=0时,式（13）为线性系统,此时,其解的形式为定幅值为A、定初相角为θ的三角函数。当ε ≠0 时,其解的形式为变幅值为A(t)、变初相角为θ(t)的三角函数。

式（13）通用解的形式为:

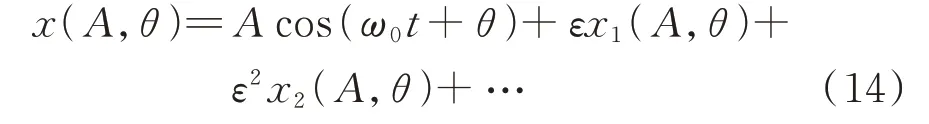
式中:x(∙),x1(∙),x2(∙),…为A和θ的函数。

在平均法中,假设系统幅值及初相角的变化远慢于系统的频率。因此,系统模型解析解可表示为:

式中:ψ=ω0t+θ。

系统模型的近似解析解可通过求解平均化方程式（16）获得。平均法的本质是将系统响应分为多个运动周期,在每个运动周期内系统处于简谐振动,而下一个周期与上一个周期相比,系统的振幅和初相角发生微小变化。

2.2 系统解析解及其稳定判据

本文借鉴平均法求解思路,假设系统模型解析解的形式为:

式中:C0为积分常数。

为求出积分常数C0,需确定系统的初始状态,即扰动前的初始值。在系统发生大扰动前,本文假定系统处于初始状态δ=δ1,此时初始条件映射到系统扰动模型式（11）中有:

解析解幅值的变化趋势决定系统扰动量的振荡趋势,进而反映系统稳定性。当解析解的幅值随时间增长而减小时,系统将逐步收敛,此时系统稳定；当解析解的幅值不变时,系统处于等幅振荡状态,此时系统处于临界稳定；当解析解的幅值随时间增长而增大时,系统振荡失稳。本文对幅值的平方进行求导,根据导数的符号判别系统稳定性。

由式（24）可定义幅值的平方Aδ为:

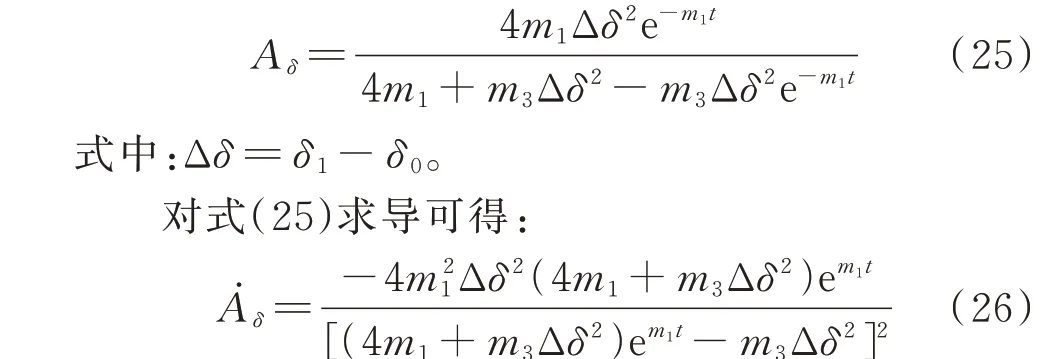
式（26）中Ȧδ<0 表明系统振荡幅值逐渐减小,因而系统稳定。此条件下,文中所获得的关系式可作为系统的大扰动稳定判据,即

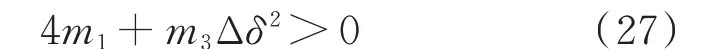
基于大扰动稳定判据式（27）,本文定义大扰动判据标识量c为:

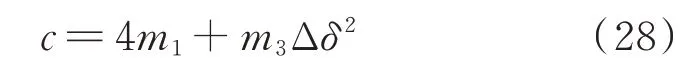
根据大扰动判据标识量表达式,可获得系统在m1-m3-Δδ三维空间下的稳定边界,如图2 所示。

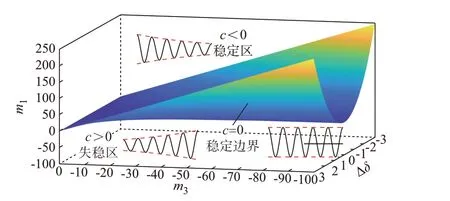
图2 大扰动三维稳定边界Fig.2 Three-dimensional stable boundary of large disturbance

当c=0 时,Ȧδ=0,此时系统处于临界稳定状态,即系统工作点（m1,m3,Δδ）位于稳定边界上。将c=0 代入式（24）整理可得系统处于临界稳定时的扰动量δd(t)为:

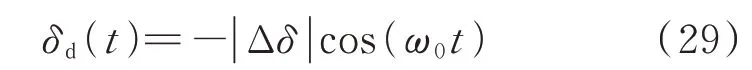
当c<0 时,Ȧδ<0,此时系统的幅值逐渐减小,如图2 中稳定区红色虚线所示,系统在大扰动后扰动量逐渐收敛,最终系统稳定。同理,当c>0 时,系统将振荡失稳。因此,通过解析解所获得的稳定标识量可以反映系统的暂态稳定性。

3 参数分析与说明

为进一步理解稳定标识量如何表征系统稳定性,本章对系统参数进一步分析和说明。式（4）的说明中提及“M>0 是保证ωn1为实数的前提”,因此本章的分析与说明均基于此前提。

3.1 非线性项

结合非线性项展开过程式（6）至式（11）,尽管sinδ项也作为非线性项参与系统稳定分析,但是根据平均化方程式（20）可以看出,平均化方法的关键积分主要是非线性函数f对变量ψ展开后傅里叶级数的一阶谐波系数,而sinδ项仅分解出高阶谐波而并未分解出一阶谐波,因此sinδ项不是系统的主导非线性项。与sinδ不同,cosδ项展开后除类似线性化得到的常数项cosδ0外,还产生平方项δ2,该项与导数项结合所产生的三倍频激发出一阶谐波参与系统稳定分析。因此,与大扰动稳定判据式（27）影响参数一致,本系统主导非线性项cosδ通过影响m1与m3进而影响稳定判据。

3.2 PLL 参数

为研究不同参数对系统稳定性的影响,将系统参数代入大扰动判据标识量,并重写大扰动判据标识量:

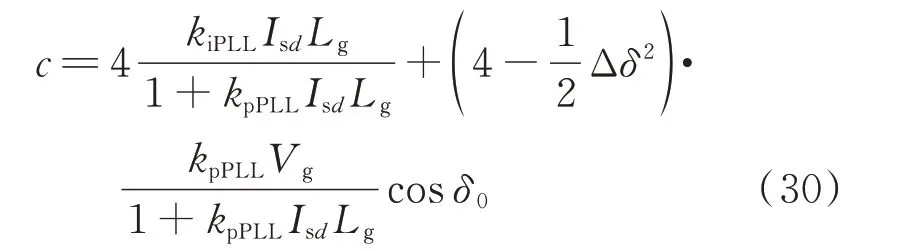
文献［24］通过等面积法分析了系统稳定点的存在性,当Δδ>π/2 时,系统工作点已越过减速区,此时系统不存在稳定点。因此,该场景并不在本文的考虑范围之内。当系统发生大扰动时,本文假定Δδ2<π2/4<8,即4-0.5Δδ2>0。

从式（30）可以看出,在M>0 的前提下,PLL积分控制参数对系统的影响关键取决于Isd。当Isd为正时,PLL 积分控制参数kiPLL与大扰动判据标识量呈正相关；当Isd为负时,PLL 积分控制参数kiPLL与大扰动判据标识量呈负相关。与PLL 积分控制参数kiPLL不同,随着PLL 的比例控制参数kpPLL的增大,大扰动判据标识量的值增大。

令式（30）中c=0,并化简可得系统关于PLL 参数空间的稳定边界曲线为:

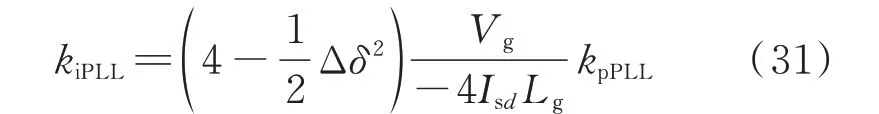
根据式（31）绘制出如图3（a）所示的关于PLL参数的二维平面示意图。当系统扰动前后的角度差Δδ为恒定时,系统的稳定边界为线性曲线。此时,系统稳定边界的斜率可以反映系统所能承受的最大扰动程度,即稳定边界的斜率越大,系统所能承受的最大扰动程度越小。

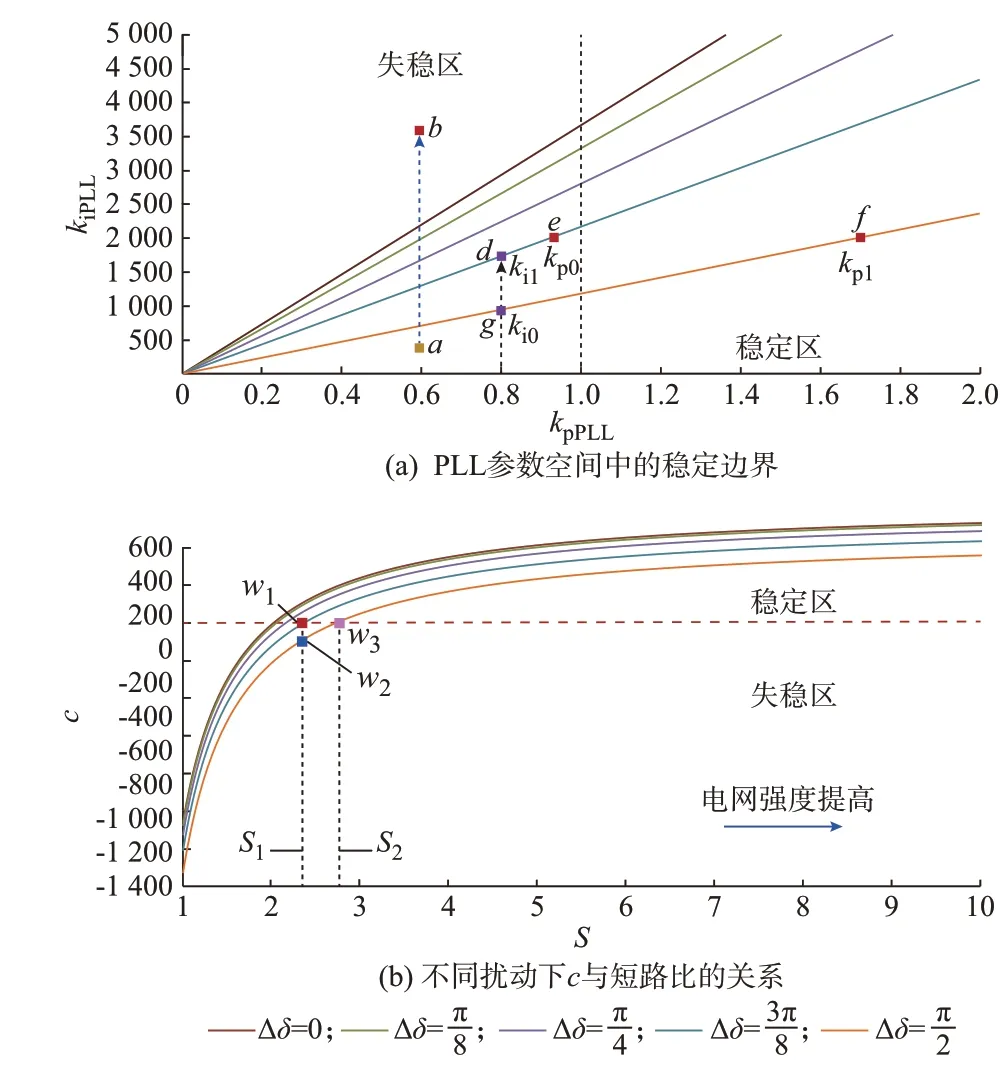
图3 PLL 参数及短路比分析Fig.3 Analysis of PLL parameters and short-circuit ratio

从图3（a）可以看出,假设扰动后系统工作在a点,此时系统处于稳定区,系统将稳定运行,然而随着PLL 积分控制参数kiPLL的增大,系统的工作点由a向b移动,此时系统已越过稳定边界,最终系统将失稳。从系统所能承受的扰动程度来看,若PLL 的比例、积分控制参数分别为0.8 和ki0,系统所能承受的最大扰动Δδ=π/2。当增大PLL 的积分控制参数使其由ki0变为ki1时,系统所能承受的最大扰动由Δδ=π/2 变为Δδ=3π/8,即稳定边界点由g变为d。可以看出PLL 的积分控制参数对系统所能承受的扰动程度有负相关的影响。同理,当增大PLL 的比例控制参数使其由kp0变为kp1时,稳定边界点由e变为f,且系统所能承受的最大扰动由Δδ=3π/8 变为Δδ=π/2。因此,PLL 的比例控制参数对系统所能承受的扰动程度有正相关的影响。

3.3 短路比

短路比作为衡量系统强弱的指标在大量文献中得到广泛应用与拓展。若系统参数固定,系统的短路比可定义为:

图3（b）为本文所提大扰动判据标识量c与S的关系示意图,其中c>0 为稳定区,其余部分为失稳区。随着S增大,电网的强度提高,c也随之增大。反之,在S较小时,系统的c急剧下降,故弱电网环境下系统发生大扰动振荡的可能性提高。若系统初始工作点为w1,短路比为S1,且发生大扰动使系统角度改变π/4,由于系统仍处于稳定区,因而系统振荡的幅值将逐步衰减。然而,随着扰动的增大,系统工作点由稳定区向失稳区偏移,例如由w1点转移至w2点,此时系统已处于失稳状态,因此系统将出现振荡失稳的现象。此时,要使系统回归稳定,需将系统的S至少提高至S2,如图中w3点。

4 仿真分析

为对理论分析进行补充说明,本文在MATLAB 上搭建如图1 所示的基于弱电网连接的并网变换器时域仿真模型。具体参数如附录A 表A1 所示。模型的正确性的验证详见附录B。

4.1 稳定判据验证

本文分析了以下扰动场景:d轴电流参考值扰动和电网侧等效电感扰动。具体场景参数变化如附录A 表A2 所示。

图4（a）为场景1 的PLL 输出角度与理论大扰动标识量的波形图。若负荷波动、控制策略等扰动使外环控制器的输出d轴电流参考值在0.5 s 时由-30 A 变为-45 A,即图中电流参考变化差Δisd,ref=15 A,此时系统d轴电流参考值的变化导致系统的c由202 变为46,c仍大于0,因此,在该扰动下系统将在一段时间的振荡后回归稳定。若系统扰动程度加剧,导致c跌落至负半轴,系统自身抗干扰能力无法维持系统稳定,最终导致失稳。需要注意的是,场景1 的扰动主要取决于系统平衡点位置差Δδ,图4（a）中蓝色曲线的振荡在初始平衡点附近,因而平衡点位置差Δδ较小,而红色曲线偏离平衡点较大,最终导致系统仍处于失稳区。

图4（b）为场景2 的PLL 输出角度与理论大扰动标识量的响应波形图。假定发电机脱机等扰动使电网侧等效电压在0.5 s 时由220 V 变为180 V或120 V,即电网侧等效电压变化差ΔVg为40 V 或100 V。如图4（b）所示,此时系统扰动导致系统的c由202 变为108 或-33,进而表明系统振荡稳定或失稳。与场景1 不同的是,场景2 所产生扰动的平衡点位置差Δδ相近,因而难以说明扰动大小而导致系统失稳。事实上,通过前文的理论分析过程可知,场景2 的参数变化主要影响m1与m3进而导致系统扰动后恢复能力下降,最终导致系统失稳。

图4（c）为电网侧等效电感扰动后PLL 输出角度与理论大扰动标识量的波形图。假定系统传输线开路、交流侧检修等使电网侧的等效电感在0.5 s 时由3 mH 变为4 mH 或6 mH,即电网侧等效电感变化差ΔLg为1 mH 或3 mH。如图4（c）所示,在0.5 s时电网侧的等效电感变化导致系统的c由202 变为97 或-114。当c为正时,系统稳定,如图4（c）中红色曲线所示；当c为负时,系统振荡失稳,如图4（c）中蓝色曲线所示。与场景1 扰动类似,场景3 扰动也通过影响系统平衡点位置差Δδ最终导致系统失稳。

4.2 参数影响

为验证PLL 控制参数与系统稳定关系,本文在不同PLL 控制参数下进行仿真,图4（d）和（e）分别为不同PLL 控制参数的系统仿真响应波形图。随着比例控制参数的增加,系统由最初的失稳逐渐变为稳定,且稳定后波动幅值也在下降。而与比例控制参数不同,积分控制参数对系统的稳定有相反的作用,与3.2 节所分析的内容相吻合。需要注意的是,在不同PLL 控制参数下,系统的平衡点并未发生变化。回顾式（8）,易发现PLL 的参数与系统平衡位置无关。

为验证短路比与系统稳定的关系,本文在0.5 s注入一个可使系统失稳的大扰动,如图4（f）所示。与3.3 节分析一致,随着扰动的注入,系统的短路比由2.0 变为1.5,为使系统回归稳定,本文在0.55 s 时对系统短路比进行调整,使其上升至2.5,最后系统回归稳定。

5 实验验证

为进一步验证本文所提暂态稳定方法及参数影响分析的有效性与正确性,本文搭建了并网变换器硬件在环测试平台。具体装置如附录A 图A1 所示,由并网变换器、交流线路、电源等组成的主电路部分在RTLAB 实验平台搭建,并网变换器控制电路由数字控制平台完成。系统的设置参数如附录A表A1 所示。

5.1 稳定判据验证

图5（a）至（c）描述了不同d轴电流扰动下的系统响应波形与大扰动标识量的测试结果。系统在0.5 s 时注入大扰动使系统d轴电流发生突变,扰动量分别为15.00、19.25、30.00 A。当系统发生不同的大扰动时,大扰动标识量均发生变化。大扰动标识量的大小代表了系统的稳定性。当大扰动标识量c大于0 时,系统将恢复稳定；当大扰动标识量c等于0 时,系统处于临界稳定状态,此时系统等幅振荡；当大扰动标识量c小于0 时,系统将振荡失稳,实验结果与本文理论分析及仿真实验一致。

5.2 PLL 参数影响验证

图5（d）和（e）分别描述了相同扰动、不同PLL控制参数条件下的系统响应波形图。在相同扰动下,PLL 的比例控制参数kpPLL由0.35 增加至0.75,系统由原来的失稳状态变为稳定状态。

5.3 系统短路比影响验证

图5（f）描述了系统发生扰动后调整短路比的响应波形图。与仿真结果一致,系统在0.5 s 时注入扰动,此时外接电网强度较弱,系统将失去稳定；在发生扰动后的0.05 s 调整系统的短路比,系统将回归稳定。

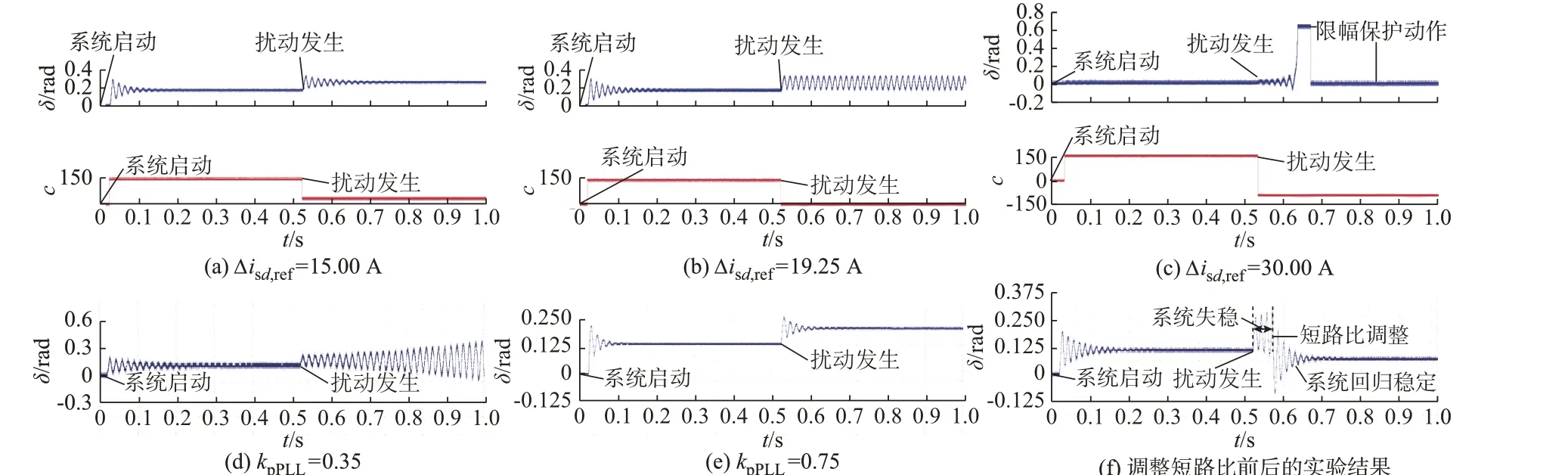
图5 实验结果Fig.5 Experiment results

6 结语

本文建立了基于弱电网环境下并网变换器的非线性二阶动力学扰动量模型,并采用平均法求解出扰动量的近似解析解,进而获得系统稳定判据,绘制稳定判据图,对关键非线性参数、PLL 控制参数及系统短路比进行分析,最终通过仿真模型与数值模型进行对比,验证解析解的正确性,并对3 种场景、不同参数进行分析,通过仿真与实验进行验证,得出以下结论:

1）本文通过非线性振动理论中平均法所获得的数值近似模型可以较准确地描述系统在大扰动前后的动态响应。

2）本文获取的稳定判据能有效评估系统的稳定性并为系统控制提供有效的理论支撑。

3）在一定条件下,PLL 比例控制参数与系统稳定性呈正相关,PLL 积分控制参数与系统稳定性呈负相关,通过本文的关系式在一定程度上可以指导PLL 的参数设计。

4）短路比作为判别系统强弱的指标之一,与系统抗扰能力具有正相关性,系统可以通过调节短路比来维持系统稳定。

需要强调的是,本文所提方法适用于大扰动下不同振荡频率的基频分量的稳定性分析,且对含有PLL 的变换器均有效。然而本文仅对单个并网变换器进行分析,并未研究多个变换器间的交互稳定。后续将基于现有研究,深入研究多个变换器间的交互机理并建立通用的模型,获得更加实用的稳定判据,为非线性控制提供理论基础。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。