基于量子粒子群混合烟花优化支持向量机的软件缺陷预测研究

崔梦天，龙松林，赵城斌，吴克奇，姜 玥，谢 琪

(西南民族大学计算机系统国家民委重点实验室，四川 成都 610041)

静态软件缺陷预测技术从20 世纪70 年代便得到初步发展，目前已被证明是提高软件可靠性和软件质量的有效方法之一[1].而作为人工智能和数据科学领域核心的机器学习理论，正广泛应用于软件缺陷预测领域.软件缺陷预测技术发展至今，已有许多学者对此进行了深入的研究，也取得了大量丰硕的成果.目前，静态软件缺陷预测技术是起步较早且发展势头较好的，简而言之，静态缺陷预测技术将软件缺陷预测问题理解为一个二分类问题，从数据中识别和区分出有缺陷样本和无缺陷样本[1].

由于项目之间存在的各种各样的差异性，无法设计出某种缺陷预测模型可以适用于所有的软件缺陷预测项目[2].研究者们对如何构建软件缺陷预测模型进行了研究[3].而支持向量机作为机器学习领域的一个代表算法，在软件缺陷预测上也得到了较多的应用，Elish 等人[4]针对NASA 数据集，将8 种机器学习方法与支持向量机(Support Vector Machines，SVM)进行了系统比较，研究结果表明:SVM 方法在总体性能上优于其它机器学习算法.

参数的选择对于SVM 的性能有至关重要的影响，随着智能优化算法的不断涌现和发展，越来越多的优化算法被应用到了SVM 参数的选择之中.杨晓琴[5]提出基于改进蝙蝠算法的软件缺陷预测模型，将蝙蝠算法引入到SVM 的参数选择中；王男帅等人[6]提出基于遗传优化支持向量机的软件缺陷预测模型，使用遗传算法来完成SVM 的参数选择工作；朱朝阳等人[7]提出基于粒子群优化SVM 的面向对象软件缺陷预测模型，以预测准确度作为适应度评价的动态惯性权重粒子群优化SVM 参数.

与原模型相比，上述方法的预测性能有了很大的提高，但仍有很大的改进空间.由粒子群算法结合量子计算理论演变而来的量子粒子群算法的算法性能，相对于原始的粒子群算法明显地提高，但其自身仍然存在算法早熟收敛的现象[8].因此，本文提出量子粒子群混合烟花算法，再基于量子粒子群混合烟花算法优化支持向量机，提高预测性能，并将其应用于静态软件缺陷预测，更有效地对软件产品进行预测和维护，减少故障发生的概率，提供给开源软件一个有效的软件质量保证方法.

1 相关工作

1.1 量子粒子群算法

量子粒子群优化(Quantum-behaved Particle Swarm Optimization，QPSO)[9]算法是PSO 算法的变种，其取消了原始粒子群算法中粒子的移动方向属性，增加了粒子位置的随机性，从而减少运行算法所需要的参数并改善了PSO 容易陷入局部最优的缺点[10].

mbest是所有个体平均最优，通过它来求解粒子出现在相对点的位置，gbest求解通过平均最好位置mbest得到.QPSO 中粒子更新步骤如下:

计算pbest的平均值mbest，如公式(1)所示:

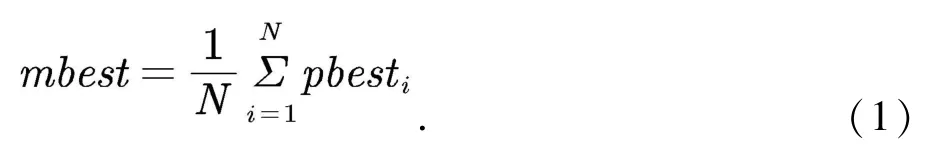
其中pbesti为局部最优值，表示每一个参数取值的变化过程中到目前为止最优适应度函数值所对应的取值；N表示粒子群大小.

计算Pi，用于第i个位置的更新，如式(2)所示:

其中gbest表示当前全局最优粒子，ø为(0，1)上的均匀分布数值.

通过式(3)对粒子位置进行更新，

其中，xi代表第i个粒子的位置，α为创新参数(一般不大于1)，u为(0，1)上的均匀分布数值，取＋和-的概率为0.5.

1.2 烟花算法

在烟花算法(Fireworks Algorithm，FWA)[11]，每个烟花被视作一个可行解，即寻找到的参数，烟花爆炸向四周放射火花也即烟花算法对邻域进行搜索的过程.

在烟花算法中，爆炸算子根据不同位置烟花的适应度值并相对于种群来计算其的爆炸半径和爆炸产生的火花数目，对于烟花xi，其爆炸半径Ri和爆炸火花数目Si的计算公式如式(4)(5)所示[12]:

对于式(5)计算出来的火花数为小数的情况，烟花算法使用式(6)将其转化成整数，并且根据适应度的好坏来限制产生火花的数量.

烟花算法通过式(7)同时产生高斯变异火花，从而增加爆炸火花种群的多样性:

上式中，xi为随机选择的烟花，k 为选择的维度.

若产生的火花不在可行区域内，则映射规则会利用式(8)将新生成的火花映射至可行域内.

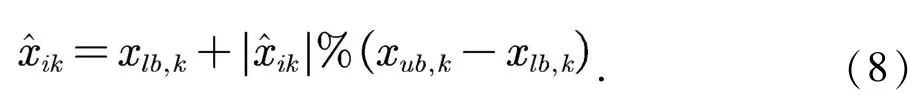
其中xub，k和xlb，k分别为解空间在维度k上的上边界和下边界.

在FWA 的每一轮迭代中，假设候选者集合为K，烟花种群大小为N.烟花算法首先从候选者集合选取适应度值最优的个体保留至下一代，而对于剩下的N-1 个烟花，候选者xi被选择作为下一代烟花的概率的计算公式如式(9)(10)所示:

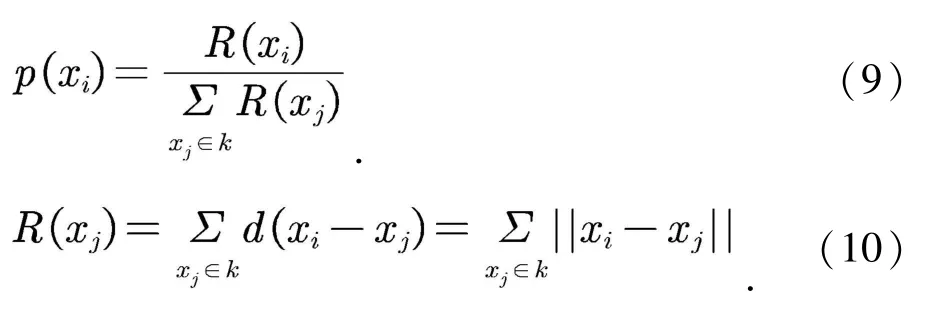
其中R(xi)为当前个体到候选者集合K除xi以外所有个体之间的距离之和，可以看出，距其它候选者越远的个体，其被选择保留至下一代的概率较大.烟花算法迭代运行，直到达到终止条件.

2 QPSO-FWA-SVM 的软件缺陷预测模型

2.1 QPSO-FWA 算法

QPSO-FWA 的思想是:把一个种群划分为个两个子种群，宏观上同时运行两种优化算法.每轮迭代中，两个子种群分别使用QPSO 算法和FWA 寻优，找出比较各自的最优解，即选出本轮迭代中的全局最优解.该QPSO-FWA 混合优化算法通过对解的不断比较、选择和迭代，对搜索范围进行了缩小，且在较大程度上克服了算法在更新解的过程中容易陷入局部最优的缺点，较为充分利用了两种算法各自所具有的局部和全局搜索能力.QPSO-FWA 混合优化算法流程如下:

第一步:对于算法的基本参数如空间中粒子和烟花的初始信息、算法的搜索空间、最大迭代次数进行初始化，设置种群大小，初始化种群.

第二步:把种群划分为2 个子种群，分别在两个不同的子种群上运行QPSO 和FWA，得到相对应的适应度值.

第三步:比较两个适应度值，选出本轮全局最优适应度值，即从中选择具有更优适应度值的参数.若迭代轮次不是S 的倍数，将更大的适应度值随机替换进入具有更小的适应度值的种群，若迭代轮次是S 的倍数，则随机交换两个种群中的T 个个体，其中S 代表的含义是每隔多少轮交换一次.

第四步:对算法进行迭代，每次都划分为两个子种群并分别运行QPSO 和FWA，得到适应度值.

第五步:重复第三步，判断是否达到终止条件(达到目标收敛精度或最大迭代次数)，若达到终止条件则算法结束，否则重复第四步，直至满足算法的终止条件.

本文提出的QPSO-FWA 算法伪代码如下所示:

2.2 QPSO-FWA 算法流程图

QPSO-FWA 混合优化算法的运行流程图如图1所示.

图1 QPSO-FWA 算法流程图Fig.1 QPSO-FWA algorithm flow chart

2.3 软件缺陷预测模型

将QPSO-FWA 算法应用于支持向量机的参数，高斯径向基核函数有一个参数σ，在参数优化的提升空间较大，且能实现非线性映射、收敛范围较大，在进行参数寻优时也具有更高的灵活性；其次，支持向量机还自带有一个惩罚因子C，用于控制对错误分类的惩罚力度.因此，本文所提出的QPSO-FWA-SVM 采取径向基核函数用于支持向量机的映射，需要优化C和σ两个参数.为了增强模型的稳定性，模型的适应度函数设置为K 折交叉验证的K 次实验所得准确度的平均值，对SVM 的参数进行优化.

如图2 所示，QPSO-FWA-SVM 软件缺陷预测模型的流程图包含如下4 个步骤:

图2 QPSO-FWA-SVM SDP 实验流程图Fig.2 QPSO-FWA-SVM software defect prediction flow chart

STEP1:获取数据集，对数据集进行分析(如TSNE)，对数据集进行简单的数据还原的处理工作，比如缺失值填补等.

STEP2:针对分析结果，对数据集进行相对应的数据预处理工作，得到用于后续实验的训练集.

STEP3:选择合适的评价指标评估模型，使用作为QPSO-FWA-SVM 对数据集进行软件缺陷预测，并设置SVM、QPSO-SVM 预测模型的对照组.

STEP4:对实验结果进行分析，评估模型的优劣.

3 仿真实验

3.1 数据集

本文采用NASA 提供的MDP 软件信息数据集[13]，包括CM1、JM1、KC1、MC1、PC3，PC4 和PC5 共7 个数据集，相关信息见表1.

表1 NASA MDP 实验数据集Table 1 NASA MDP Datasets

由表可知，MDP 数据集存在较为严重的数据不平衡问题(有缺陷样本量数远小于无缺陷样本数)，且数据维数过高，故对数据集做如下预处理工作:

1)对数据集采用SMOTEENN 方法进行采样，使得有缺陷样本数与无缺陷样本数相当，由于分类模型对于平衡数据具有高灵敏度，使得实验结果具有说服力.

2)利用主成分分析(PCA)对数据集进行特征选择，选择特征值贡献率大于90%的特征所对应的特征子集进行实验.

3)基于SVM 的特性，若不对数据进行归一化(Normalization)，可能会导致SVM 无法收敛，且归一化在一定程度上可以避免数值计算不稳定，并能使得模型参数以较快的速度收敛.

3.2 评价指标

为了证明本文方法的有效性，通过使用准确率、查准率、查全率及F1 值这些通用指标进行比较.这些指标都是从混淆矩阵中推导出来的，混淆矩阵如表2所示[14].

表2 混淆矩阵Table 2 Confusion matrix

相关的定义如下[15-17]:

准确率表示模型所得分类结果中，预测与实际相同的测试实例与所有测试实例个数的比值，即

精确度也叫做查准率，表示模型所得分类结果中，被正确预测的正例与预测为正例的样本总数之比，即

查全率表示预测正确的正例与实际容易出错的模块的比值，即

F1 值是对查准率和查全率进行整体评价，计算公式如下:

3.3 实验结果与分析

实验采用K 折交叉验证(K-Fold Cross Valiadation)方式(K 根据数据集的大小来确定)来检测模型的预测能力，将K 次实验所得准确度的平均值作为QPSO-FWA 算法的适应度对SVM 的参数进行优化，并使用对应的参数代入SVM 得到其他评价指标作为实验结果.针对所选择的7 个数据集进行实验，得出了传统SVM、QPSO-SVM 和本文提出的QPSO-FWASVM 方法的预测结果.对于SVM 来说，若设置较大惩罚因子则算法对出错样本的容错率低，但同时会降低模型的泛化能力，可能导致模型过拟合，所以将参数的范围设置为(0，100]进行参数的寻找，同时因为采用交叉验证的平均值来作为适应度，一定程度上规避了模型的过拟合的可能性，具体实验结果即各个评价指标见表3.

表3 缺陷预测模型性能指标Table 3 Defect prediction model performance indicators

通过表3，可以直观地看出，在准确度、查准率、查全率和F1 值上，本文提出的QPSO-FWA-SVM 软件缺陷预测模型在整体上要优于经典SVM 和QPSOSVM.在准确率这项指标上，QPSO-FWA-SVM 软件缺陷预测模型在7 个数据集上的表现均优于其他两个模型，原因是实验是使用准确度作为适应度函数进行最大化，从而寻找最优参数.在查准率上，除在MC1数据集上较经典SVM 值低以外，在其他数据集上，QPSO-FWA-SVM 模型均优于另外两个模型，QPSOFWA-SVM 在MC1 上的查准率为0.87，而经典SVM为0.94.其次QPSO-FWA-SVM 的查全率指标除在PC3 和KC1 上表现不如另外两个模型之外，在其他数据集上均相较更为优秀，且在PC3 上的表现也达到了0.92.

F1 值可以综合评价查准率和查全率，虽然本论文提出的模型在查全率和查准率没有做到完全优于另外的模型，但是在F1 值上的表现，本文提出的QPSO-FWA-SVM 软件缺陷预测模型均是最优值，充分说明了QPSO-FWA-SVM 的优越性.

QPSO-FWA 算法在QPSO 的基础上混合了FWA算法，提高了QPSO 跳出局部最优的能力.值得注意的是，CM1 数据集共327 条数据，QPSO-FWA-SVM 的在CM1 数据集上的10 折交叉验证准确率达到94%，说明该模型在小样本的情况下也具备较好的预测能力.

4 结语

本文提出了量子粒子群混合烟花优化算法，用于对支持向量机的参数寻优，将两种算法进行融合，进行参数寻优，从而达到更好的软件缺陷预测效果.其次，本文基于NASA MDP 数据集进行仿真实验，将混合烟花算法的量子粒子群算法、量子粒子群算法用于SVM 的参数寻优，并且与经典的SVM 之间进行对比，通过各项评价指标，证明了QPSO-FWA-SVM 软件缺陷预测模型的有效性和优越性.同时，通过实验对比表明量子粒子群混合烟花算法对量子粒子群算法跳出局部最优的能力有较大程度的改进.