超临界流体流动加速效应及其判别式研究进展

黄 宇， 段伦博

(1.东南大学 能源热转换及其过程测控教育部重点实验室，南京 210096；2.东南大学 能源与环境学院，南京 210096)

符号说明：

Ac、KV、θ——流动加速因子

cp——比定压热容，J/(kg·K)

d、D——管内径，m

G——质量流速，kg/(m2·s)

k——热导率，W/(m·K)

p——压力，Pa

Pr——普朗特数

q——热流密度，kW/m2

q+——无量纲热流密度

Re——雷诺数

T——温度，K

u——流速，m/s

x——距加热段入口处的距离，m

αp、β——体积膨胀系数，K-1

βT——绝热压缩系数，Pa-1

δ——边界层厚度，m

μ——动力黏度，kg/(m·s)

ν——运动黏度，m2/s

ρ——密度，kg/m3

τ——切应力，Pa

H——焓，kJ/kg

下标

ac——流动加速效应

b——流体

i、in——管内

w——壁面

超临界流体(SCF)狭义上指流体温度和压力均超过其临界点，而广义上则包括压力超过临界压力而温度低于临界温度的流体。Pioro等[1]对20世纪初以来SCF的发展进行了详细介绍，并描述了SCF在动力工程应用中的热工水力特性。随着超临界二氧化碳布雷顿循环和超临界水冷却核反应堆(SCWR)的兴起，SCF的对流传热研究得到了广泛关注，且SCF在太阳能、核能和燃煤等领域得到了蓬勃发展。

一般认为，SCF的比定压热容最大时对应的温度为准临界温度(Tpc)，在该温度附近SCF的密度、比定压热容、热导率和动力黏度等物性参数均会发生较大变化，而流体密度的剧烈变化是导致浮升力效应和流动加速效应出现的根本原因。SCF在管内进行对流传热时，由于近壁面附近流体温度与主流区温度相差较大，导致沿径向方向流体存在较大的密度梯度，从而产生浮升力效应[2]。由于加热管内沿程温度升高以及压力减小，导致SCF体积膨胀，流速增大，使得边界层内切应力减小，进而抑制湍动能的生成并使壁面热阻增大，该现象称为流动加速效应[3]。一般来说，浮升力效应随管径的增大而增强，而流动加速效应往往在微细管中更加重要[4]。浮升力效应对传热的影响与浮升力和流动方向有关，而流动加速效应的方向一般与流动方向相同，因此总会起到弱化传热的效果。

近年来，已有许多学者探究了流动加速效应对SCF传热的影响，但对于其判别式以及同一判别式的阀值选择还未达成共识。笔者针对现有常规直管所选用的流动加速判别式进行了对比分析，讨论了判别式存在的问题。最后，基于非常规直管，探究了现有判别式的准确性，并对未来流动加速效应及其判别式的发展进行了展望。

1 直管流动加速判别式及其阀值

针对常规直管内所选用的流动加速判别式及其阀值汇总见表1[5-16]。当流动加速因子大于阀值时，流动加速效应对传热的影响不可忽略。

表1中的流动加速判别式大体上可分为2类，即仅考虑主流区物性变化引起的流动加速效应的判别式和从边界层切应力变化角度出发提出的判别式。通过对比不同的判别式和阀值，可以发现：

(1) 很多学者采用Mceligot等[3]提出的判别式对不同工况下SCF的流动加速效应进行了分析，然而流动加速判别标准却不恒定，这说明学者对阀值的选取还没有达成统一。

(2) Bovard等[13]和Liu等[14]所采用的判别式较为相似，前者基于理想气体状态方程，后者采用van der Waals方程进行理论推导。由于van der Waals方程更加贴近CO2的状态变化，因此Liu等提出的判别式能更准确地计算超临界CO2(sCO2)所受到的流动加速效应。

(3) 除Jiang等[10]所研究的微细管外，其他学者所采用的判别式均不包括由于沿程压降造成的流动加速效应(KVP)，而仅考虑由于沿程温度变化导致的流动加速效应(KVT)。当管内径小于0.1 mm时，由于压降引起的流动加速效应对传热的影响不可忽略。

(4) 由于流动加速效应的方向总与流动方向相同，因此流动加速判别式的适用性不受流动方向限制。

2 流动加速效应

结合前文的判别式和阀值，研究人员计算了不同工况下的流动加速效应，并对传热恶化现象进行了解释。部分学者在此基础上结合努塞尔数Nu或壁面温度的变化趋势进行了更深入分析，进一步验证所选择的流动加速判别式阀值的准确性。

在系统压力为8.6 MPa、入口温度为30 ℃、质量流量为0.12 kg/h和入口Re为2 900时，Jiang等[5]计算得到的流动加速因子分布见图1。从图1可以看出，当qw≥57.6 kW/m2时，在管上游流动加速因子为9.5×10-7～2.5×10-6。根据所选阀值(9.5×10-7)，可以认为此时流动加速效应会减弱湍流强度，并对对流传热产生抑制作用。Jiang等[5]对比了流动加速效应与浮升力效应对局部Nu的影响，发现高热流密度下的传热弱化主要是由流动加速效应造成的。值得注意的是，如果选择流动加速判别式阀值为3×10-6，则浮升力效应和流动加速效应均可被忽略，此时将无法解释高热流密度下的传热恶化现象。

表1 竖直和水平管内流动加速效应判别式

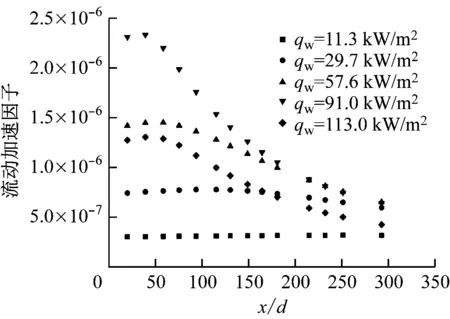
图1 sCO2竖直向上/下流动时流动加速因子的沿程变化[5]

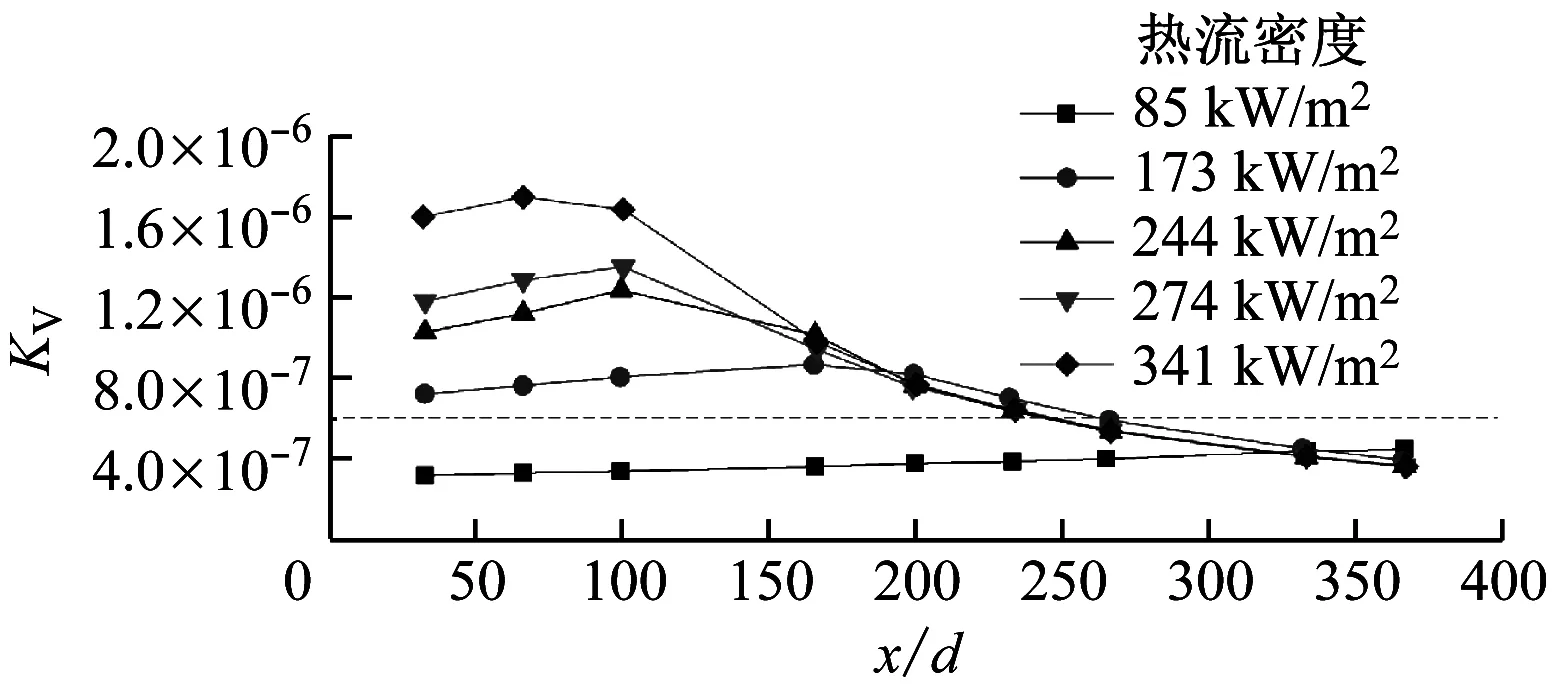
在入口压力为7.7～7.8 MPa、入口温度为297 K、质量流速为1 823 kg/(m2·s)和入口Re为2 600条件下进行实验，Jiang等[10]发现此工况下KVP的数量级仍为10-7，如图2所示，表明此时由于管内压降产生的流动加速效应不能忽略。观察Nu的变化曲线可以发现，在x/d=100处存在局部传热恶化现象。当KV>6×10-7时，流动加速效应会明显抑制对流传热的进行，说明此时Murphy等[17]提出的判别式阀值(9.5×10-7)不再适用。

在q=22.2 kW/m2条件下管的下表面无量纲热流密度q+和实验得到的NuEXP与通过Gnielinski公式计算得到的NuGn的比值(NuEXP/NuGn)的沿程变化见图3。当质量流速为250 kg/(m2·s)时，管的下表面发生传热强化。Kim等[12]认为仅通过流体温度Tb下的物性计算q+，而没有考虑壁温对各物性的影响，因此不能解释流动加速效应对传热的影响。

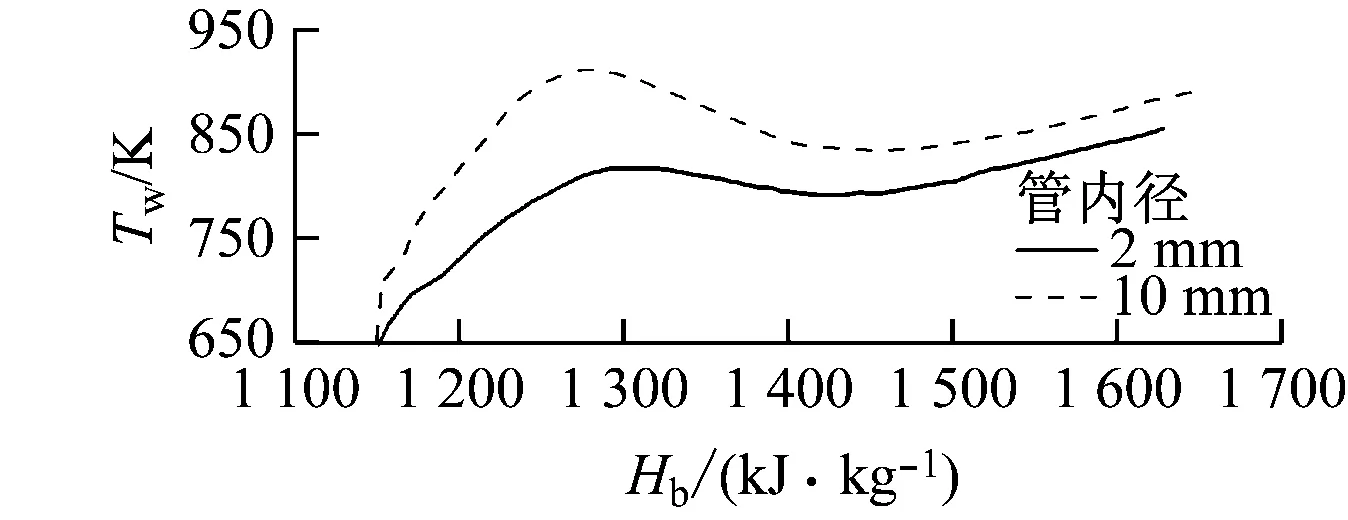
如图4所示，在Tin=623 K、p=3 MPa、qw=500 kW/m2和G=704 kg/(m2·s)条件下,Cheng等[8]模拟计算了无重力时管壁温的变化情况。由图4可知，在没有浮升力效应时仍存在传热恶化现象，尽管此时对应的KV均小于3×10-6，但不能忽略流动加速效应对传热恶化产生的影响。这也间接说明根据其他SCF实验和模拟结果提出的流动加速判别式阀值可能不再适用于超临界碳氢燃料。

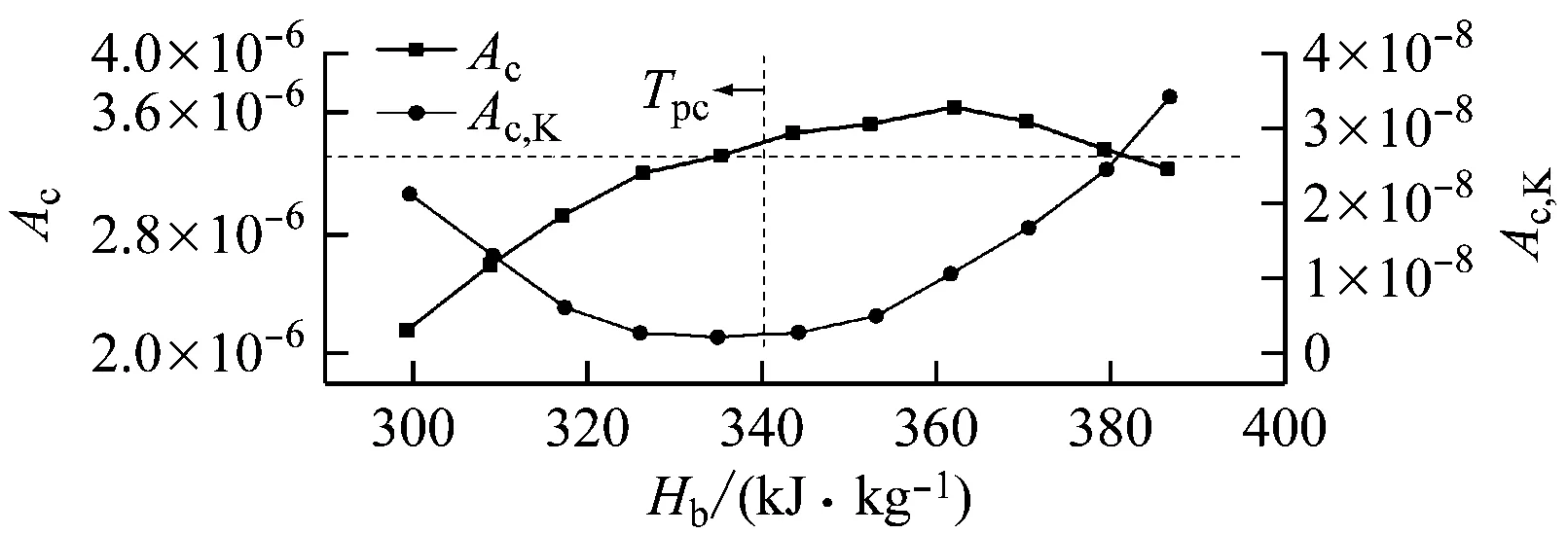
如图5所示，在p=7.61 MPa、Tin=30.5 ℃和G=901.8 kg/(m2·s)条件下通过与Kim等[18]提出的流动加速因子Ac,K进行比较，Liu等[14]发现当热流密度为175.9 kW/m2时浮升力效应可以忽略，而所提出的流动加速因子Ac在准临界区域存在峰值，当Ac不低于3.3×10-6时，传热恶化的发生是由于流动加速效应。此时，Ac,K在准临界温度附近出现最小值，在远离准临界温度时出现最大值，不能对准临界区域附近发生的传热恶化进行解释，说明采用更能准确反映CO2状态变化的van der Waals方程推导得到的Ac更为合理。

(a)

(b)

(b)

(a)

(b)

(1)

(a)

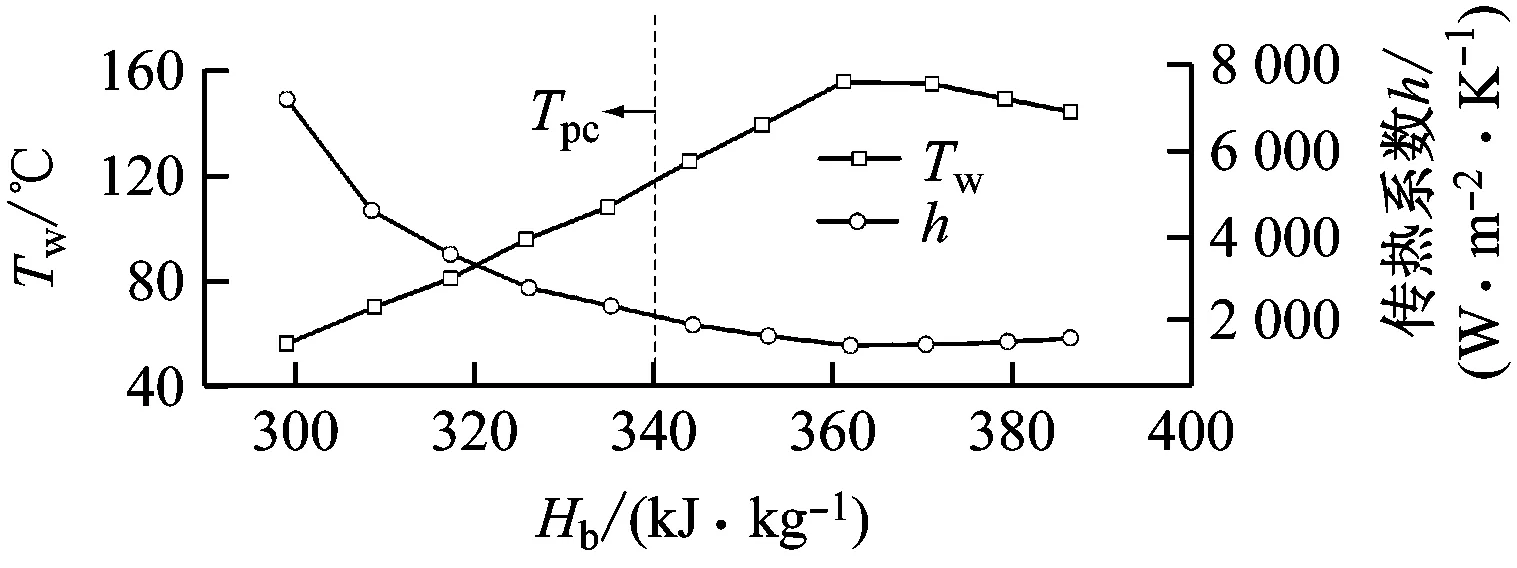
(b)

应用前文所述流动加速判别式对常规直管内的传热恶化现象进行解释时，存在如下现象：

(1) 在Jiang等[5]的实验结果中，如果采用Mceligot等[3]提出的流动加速判别式阀值，则可能会忽略流动加速效应对传热的影响，导致传热恶化不能通过浮升力效应和流动加速效应进行解释。Jiang等[10]在低Rein和pin下通过对比浮升力效应和流动加速效应对Nu的影响，发现Murphy等[17]提出的判别式阀值(9.5×10-7)可能过高，这可能会忽略此时流动加速效应对传热的影响；而在高Rein和pin下，Murphy等[17]建议的阀值是适用的。这说明流动加速判别式阀值的准确性对于流动加速效应能否合理解释传热恶化至关重要。

(2) 当管内径为微米级时，由管内压降造成的流动加速效应不可忽视。

(3) 当浮升力效应被忽略时，一般可通过Nu的变化情况来对流动加速判别式阀值的准确性进行验证。

3 非常规管流动加速效应的研究

在包括SCWR、气体冷却器和换热器在内的实际工业应用中，大多不是单一的圆形光滑直管，而多选用非圆形截面直管、环形管、螺旋盘管和管束等。因此，研究非常规管内的流动加速效应并评估由光滑直管推导得出的流动加速判别式在非常规管内的适用性是非常重要的。

Zhang等[19]对竖直螺旋盘管内的sCO2对流换热特性进行了模拟，探究了流动加速效应对传热的影响。基于Mceligot等[3]和Mikielewicz等[20]的研究成果，结合归一化处理，得到流动加速因子θ：

(2)

如图6所示，通过分析无重力下sCO2传热系数hng与hc(hc为忽略流动加速效应和浮升力效应的传热系数[19])之比随q+的变化情况，发现当q+大于4.5×10-4时由于流动加速效应引起湍流的近层流化，使得传热受到抑制。这表明q+=4.5×10-4时可以较为准确地反映竖直螺旋盘管内流动加速效应对传热的影响。

图6 hng/hc随q+的变化[19]

考虑到现有非常规管内流动加速效应的研究较少，笔者对水平U形管内sCO2的流动加速效应进行数值研究，其中该U形管180°回转型弯头直径为40 mm，管内径为1.82 mm，管外径为2.2 mm，加热段长度为500 mm。采用有限体积法对三维稳态控制方程进行求解，湍流模型选用带有增强壁面函数的RNGk-ε模型。经分析发现，网格数为256万时可以达到网格无关性，y+<1时可以保证近壁面流体流动和传热的精确捕捉。计算工况为p=8 MPa、qw=80 kW/m2、G=400 kg/(m2·s)、Tin=20 ℃，分别设置g=0 m/s2(忽略浮升力)及sCO2密度恒定(忽略浮升力和流动加速效应)。通过忽略浮升力和流动加速效应时的传热系数hnBA与忽略浮升力时传热系数hnB的比值可定量表示流动加速效应对传热的影响。

如图7所示，由于流动加速效应对传热的弱化作用，导致hnBA/hnB均大于1。选用表1中Wang等[7]、Kim等[12]、Gu等[15]和Liu等[14]所采用的流动加速判别式计算水平U形管内的沿程流动加速效应。

(a) KV判别式[7]

(b) q+判别式[12]

(c) Ac判别式[15]

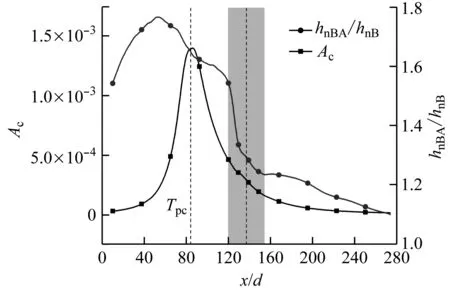
(d) Ac判别式[14]

由hnBA/hnB和流动加速判别式计算得到的流动加速因子沿程变化均为先增大后减小，但流动加速因子最大值出现的位置不同。这可能是因为流动加速判别式大多以整体流体温度下的物性参数进行计算，然而在流体温度达到Tpc之前，近边界层流体温度已达到Tpc，诱使流动加速因子最大值向入口迁移。U形管入口处的hnBA/hnB明显大于出口处，说明在此工况下流动加速效应在入口处对传热的影响更强。流动加速因子KV和Gu等[15]提出的Ac公式可定性反映这一趋势，而q+和Liu等[14]提出的Ac则不能。在水平U形管弯管段(图中阴影部分)由于离心力的出现增强了管内的二次流强度，使流体密度沿流动方向变化梯度减小，促使流动加速因子更快减小。此外，计算域中KV均小于其判别式阀值，但此时管子内部流动加速效应不可忽略，说明其判别式阀值不适用于水平U形管。

4 结 论

(1) 总体来说，对于SCF流动加速效应的研究远少于浮升力效应，且针对竖直管内的研究多于水平管，在非常规管内探究流动加速效应的模拟和实验研究极少。

(2) 针对常规直管，大多采用流动加速因子KV对流动加速效应进行分析，部分则选用无量纲热流密度q+和理论推导得出的流动加速因子Ac，然而研究人员对于判别式和判别阀值的选择还没有达成共识。

(3) U形弯头的存在会抑制流动加速效应对传热的影响，而由直管理论推导得到的流动加速判别式不能反映该现象。

5 展 望

针对流动加速效应及其判别式的研究应重点关注以下方面：

(1) 在非常规管和非均匀热流密度下，对基于光滑直管理论推导出的流动加速判别式所作出的假设进行修正，推导适用于实际工业应用的流动加速判别式及阀值。

(2) 不同工况下流动加速对传热影响的判断标准可能不同，因此需要深入研究。应探究包括Re、近壁面和主流区剧烈物性变化对流动加速效应判别式阀值的影响。

(3) 近年来，以印刷电路板式换热器(PCHE)为代表的SCF微纳尺度传热受到了广泛关注，在未来有较为广阔的发展空间。微纳管中由于压降产生的流动加速效应可能是未来SCF微细尺度传热研究的重点。