基于小波分析理论的桥梁监测信号去噪研究

王 刚

(山西路桥东二环高速公路有限公司，山西 太原 030006)

0 引言

随着社会经济的迅猛发展，交通行业的重要性日益凸显，桥梁的建设和运营亦如火如荼。桥梁的建设施工和运营过程中，在材料、温度、风速、荷载变换及地震等因素的影响下，桥梁容易发生各类结构变化，极易产生潜在的风险因素进而导致桥梁事故的发生。因此，桥梁的健康监测越来越受到重视。

然而，在桥梁的健康监测中，信号极易受各类环境因素的干扰和影响，导致采集的信号中含有大量杂乱无章的噪声和突变。因此，桥梁监测信号的去噪处理显得尤为重要。

小波变换(Wavelet Transform)是近年来迅速发展的一个新领域[1]。它作为一种多尺度分析工具，不仅很好地继承了傅里叶变换，更是完善了傅里叶变换。与傅里叶变换相比，它的主要优势在于能够将信号进行分解，分解为与原函数不同位移及分辨率的小波函数形式，细化分析问题部分的信息，从而对原信号进行多尺度细化分析。因此，小波变换又有“数学显微镜”之称，可用来分析非平稳信号[2]。小波分析在诸多领域有着广泛的应用，包括量子力学、图像处理、信号分析、桥梁健康监测等，并取得丰硕的成果[3]。

1 小波分析理论

1.1 傅里叶变换

傅里叶变换的核心内容就是将信号分解为若干个不同频率连续正弦波，并且将这些分解出来的正弦波相互叠加[4]。通过这一变换，可以分析出信号中各频率的成分。傅里叶变换作为纯频域分析方法，其缺点也是显而易见的，即无法辨别信号中的时域部分。

傅里叶变换公式如下：

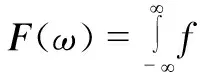
(1)

1.2 小波变换

小区域的波即为小波。母小波的定义为：设ψ(t)∈L2(R)为可积函数，则其傅里叶变换F(ω)满足：

(2)

母小波具有波动性和带通性。

若母小波是连续的，则可得到如下关系

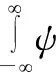
(3)

在对非平稳信号进行分析时，小波变化具有傅里叶变化所不具备的时频分析局部化能力。此外，正交、二进小波变换对频域进行分析时，具有分割二进频带的能力。

2 小波分析在去噪方面的应用

在桥梁的监测过程中，受环境等多重因素的影响，导致监测信号中都带有噪声，这对桥梁的监测是不利的[6]。小波分析就是依靠其较强的去相关性，对桥梁监测中的信号进行小波变换，将原始信号和噪声进行有效分析。通过小波分解，根据幅值的大小对噪声和有效信息进行区分，从而做到将绝大部分噪声去除。

2.1 小波分析去除奇异点

傅里叶变换作为研究函数奇异性的一种方法，其缺点较为明显，即缺乏时域局部分析能力[7]。傅里叶变换在研究函数奇异性时，只能确定其整体性质而不能准确确定奇异点的时域位置和分布，因此傅里叶变换不具备局部分析的能力。

小波分析具有很强的时域局部化能力，可用来分析信号奇异点的时域位置和分布。

本文采集了部分原始信号波形，并计划使用小波分析检测其中的奇异点，同时将奇异点进行消除。如图1所示，在T=1 195和T=1 211处存在奇异点。拟使用db3小波对信号进行局部的分解，得到细节信号图，如图2所示。从图2中可以看出，细节信号d1、d2中包括了奇异点。在对信号进行重构时，将d1、d2及d3消除，可得到图3。对比图1及图3可以发现，奇异点已经基本消除。

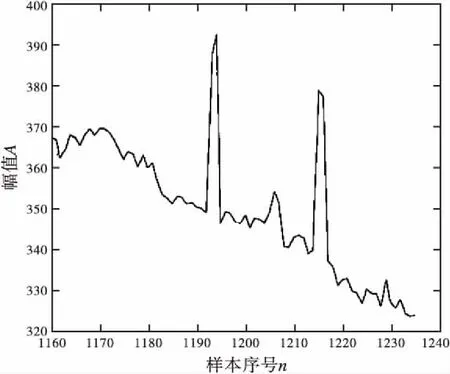
图1 原始信号波形图

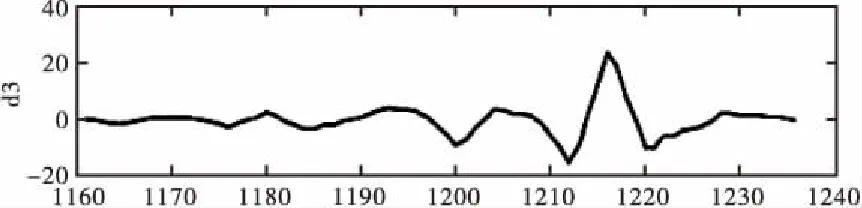
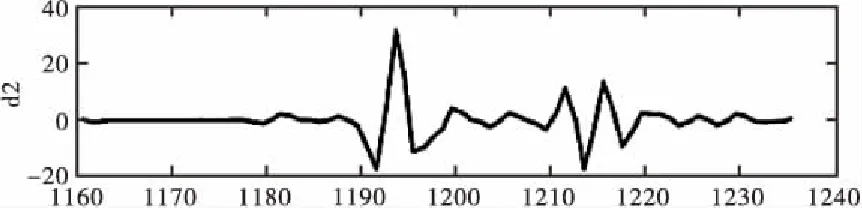
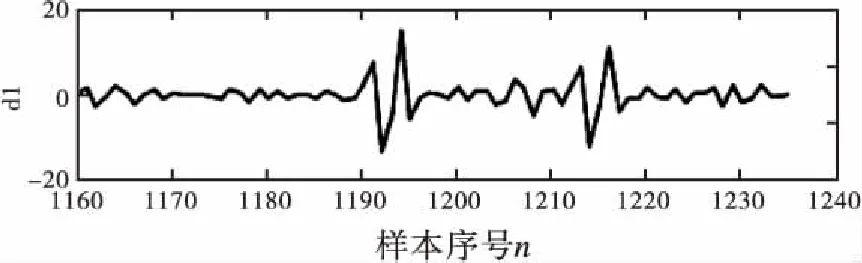
图2 小波分解的细节信号波形图

图3 消除奇异点后的波形图

如图4所示，本文采集了含奇异点的原始信号。为了确定该奇异点的具体时间点，采用haar小波对其进行小波变换。先用矩阵将原始信号进行表值，其大小为1×1 024，精度为双精度。

图4 原始信号示意图

对原始信号采用小波变换，采用db6小波，尺度范围为1～32之间。其处理后图像如5所示。

图5 db6连续小波变换后系数图

从图6可看出，经haar连续小波变换后的图，可明显在T=715时发现一个倒锥图形。因此，可判断出该区域内存在奇异突变点。

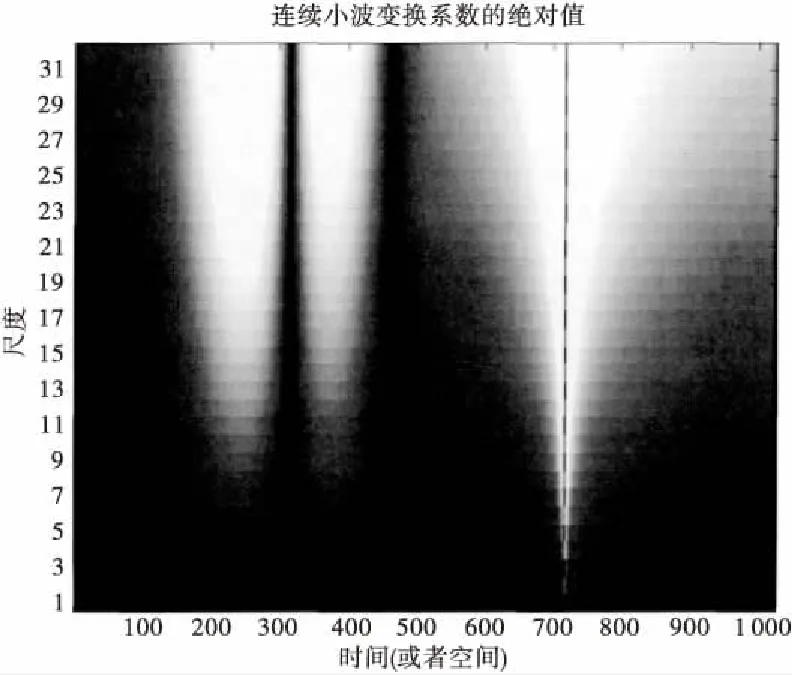
图6 haar连续小波变换后系数图

2.2 小波阀值去噪

2.2.1 阀值选取

阀值的选取在信号去噪的过程中至关重要[8]。我们将原始信号记为f(t)，其小波系数为ωjk，通常将其简记为ω。将运用阀值处理后的系数记为η(ω)，η(ω)为阀值函数。通常，我们在选用阀值时有硬阀值和软阀值两类函数。

硬阈值函数：

(4)

软阈值函数：

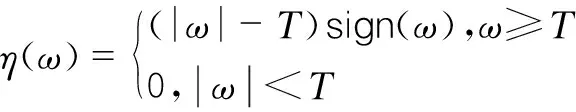
(5)

在ωT时，硬阀值和软阀值的处理就有所区别。硬阀值在|ω|>T时，全部保留ω值，这样可以完整地留下原信号的边缘特征。但在|ω|=T时，采用硬阀值处理原信号函数会导致信号重构时产生震荡现象。相比硬阀值，软阀值在|ω|>T时对ω进行收缩处理，这虽然可以使系数的连续性更好，但却使得η(ω)与ω之间存在恒定的差值。这些差值会在后续的重构中，影响其性质。

针对两类阀值的优缺性，选用合适的阀值，或结合两类阀值的优缺点进行改造，构造出去噪效果更佳的阀值函数。

2.2.2 阀值估计

在去噪过程中，无论选用软阀值还是硬阀值，都需要确定其阀值[9]。因此阀值的选取至关重要，直接影响重构信号的准确值。若选取的阀值偏小，则难以有效去除噪音；若选取的阀值偏大，则会导致原始信号中有效信号丢失。我们通常采用以下阀值公式：

(6)

其中，T——噪声函数；N——信号长度。

在实际的去噪过程中，通常T需要随着信号函数的改变而改变。因此，在T值的选取中，需要将信号函数的平稳性和信噪比考虑进去。在面对平稳性较差的信号时，T应当选取较小值；当信号的平稳性较强时，则应选取较大的T值。当信号的信噪比较大时，应选取较小的T值；当信号的信噪比较小时，应选取较大的T值。

3 仿真实测信号分析

本文选取桥梁监测过程中的部分动应变信号数据，对其进行去噪处理分析。选用几类常见的小波基及阀值对信号数据进行预处理，得到以下数据，如表1所示。

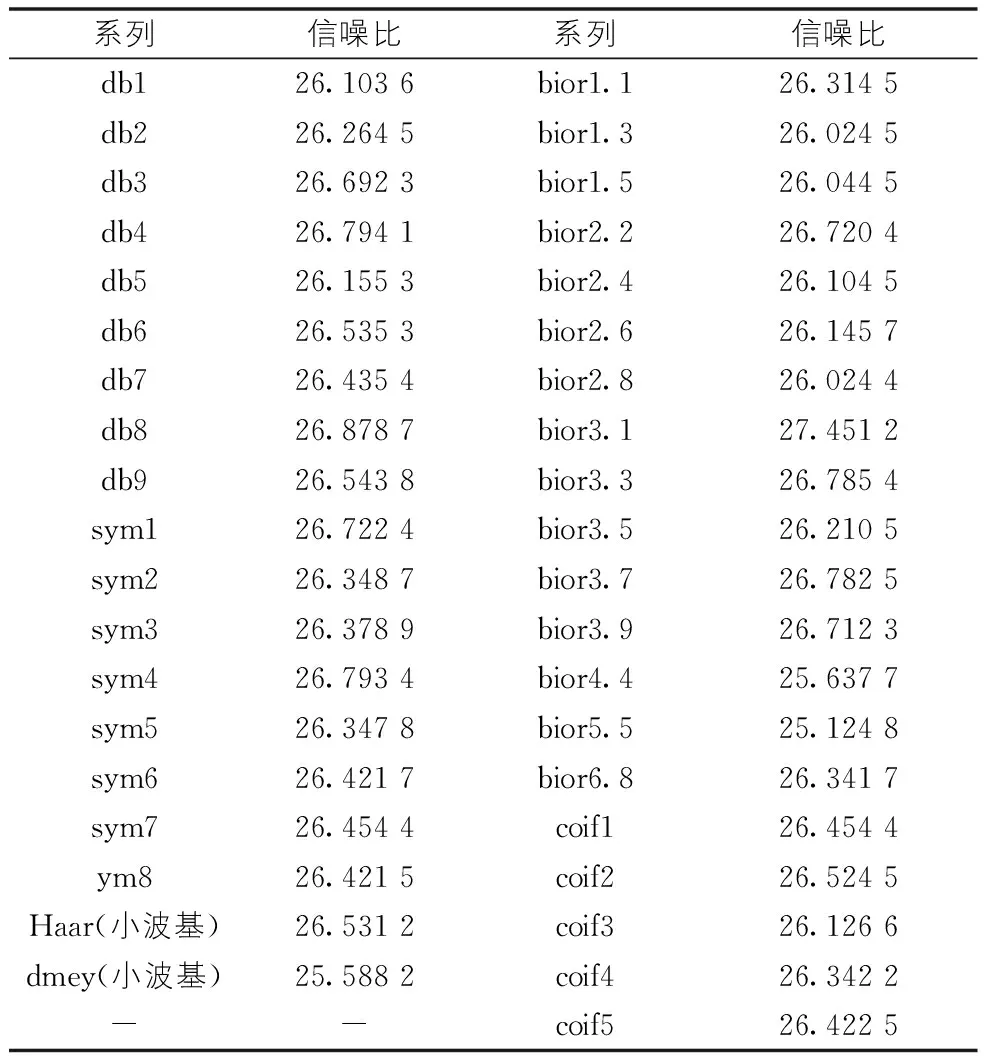
表1 去噪效果对比表

通过对表1中的数据进行简单的对比分析可知，对于实测的动应变信号而言，小波基bior3.1在进行6层分解后能够取得最高的信噪比27.451 2，故采用bior3.1作为本次信号实测分析的小波基。

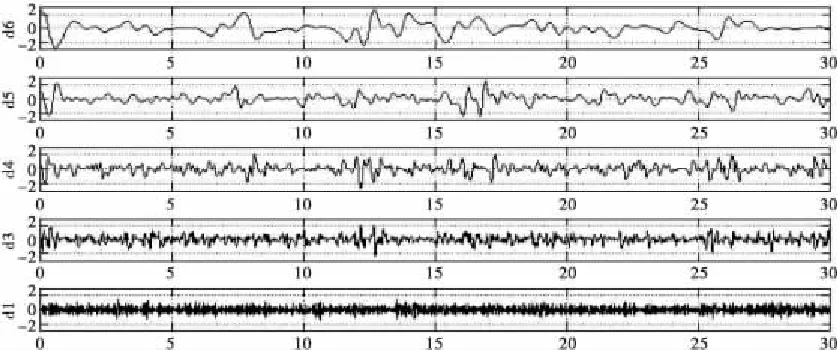
图7 高频系数图

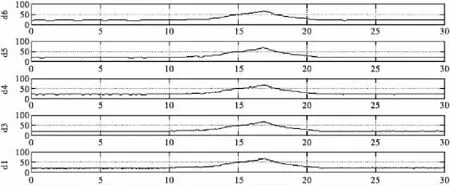
图8 低频系数图

多尺度分解如图7～8所示。其中，a1～a6及d1～d6分别为原始动应变信号经各层分解后的低、高频信号。

在经过6层小波分解后，容易辨别出该原始动应变信号的峰值以及该段突变段的起点及终点。而选择了bior3.1作为本次的小波基函数后，接着进行阀值规则的选择。通常，一般选用Rigrsure、Heursure、Sqtwolog和Minimaxi等阀值规则，用于对局部信号的阀值预估，分别采用软、硬阀值对分层处理后的信号进行处理[10-11]。将经软、硬阀值处理后的信号进行重构，得到去噪后的信号。

下表为四种阈值规则对动应变信号去噪的效果对比。

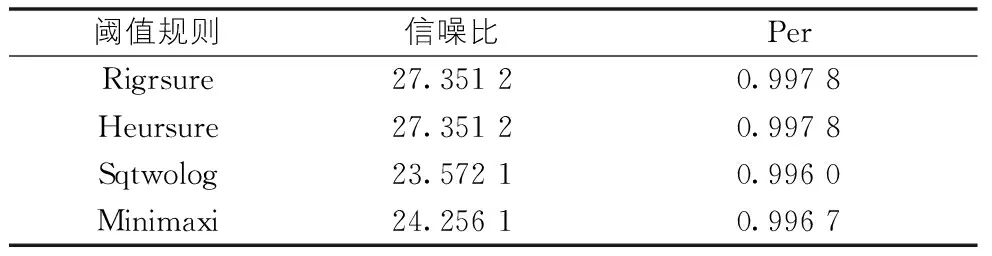
表2 去噪的效果对比表

通过对表2进行简单的数据对比可以发现，Rigrsure规则或Heursure规则可以得到较高的信噪比和per值。因此，本文在后期的小波阀值去噪过程中采用Rigrsure规则。采用Rigrsure阀值规则对信号分别采用软、硬阀值去噪，如图9所示。

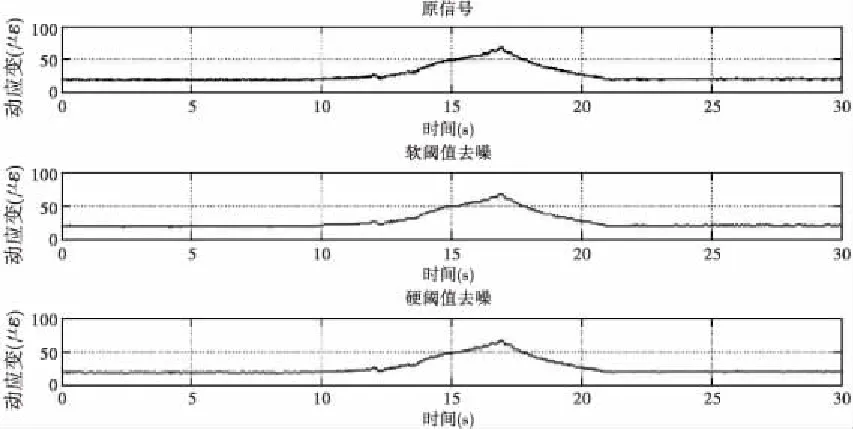
图9 软硬阈值去噪对比图

对比图9中的原始信号、软阀值去噪和硬阀值去噪可以发现，原信号中存在大量的噪声，而在采用了Rigrsure阀值规则进行小波软、硬阀值去噪后，有效减少了噪声。将软、硬阀值的去噪效果进行对比可以发现，软阀值去噪后的波形比较平滑；而硬阀值处理后的波形则存在着突变的点及不连续现象。因此，本文采用软阀值进行后续的去噪工作。将原信号及经软阀值去噪后的信号进行傅里叶变换，得到频谱图10。

图10 频域对比图

对图10进行观察可以发现，经傅里叶变换后的频域图和原信号的频域图十分接近。经傅里叶变换后的频域图毛刺图像明显减少、波形更加平滑，表明基于Rigrsure阀值规则的小波去噪方法对动应变信号的去噪效果明显。

4 结语

本文主要介绍了小波分析理论在实际采集数据案例中的应用。通过对小波变换和傅里叶变换的对比，发现了小波变换在时域局部化分析方面的独特优势。同时，介绍了小波分析在桥梁监测信号去噪方面的应用，包括小波分析去除奇异点和小波阀值去噪。最后，运用小波分析方法，对采集的桥梁动应变监测信号进行分析处理。不同的小波基、阀值规则和软、硬阀值的处理方法都会对去噪效果产生影响，针对此次采集的动应变信号，采用bior3.1小波基能取得最高的信噪比。同时，在此基础上采用Rigrsure阈值规则能得到信噪比和per值。最后，通过软、硬阀值处理结果的对比，选定去噪效果更佳、波形更为平滑的软阀值作为去噪方式。

[1]庞晓清.桥梁检测中信号处理及模态分析[D].湖北：武汉理工大学，2007.

[2]Mallat5.A Theory for Multiresolution Signal Decomposition：the Wavelet Representation[J].IEEE Trans.On PAMI，1989，11(7)：673-693.

[3]冉启文.小波分析方法及其应用[M].哈尔滨：哈尔滨工业大学出版社，1995.

[4]Farge M.，Wavelet Transform and Their Applications to Turbulence[J].Annual，Rev Fluid Mech，1992(24)：522-531.

[5]崔锦泰著，程正兴译.小波分析导论[M].西安：西安交通大学出版社，1995.

[6]Felber A.J.Development of a Hybrid Evaluation System[D].University of British Columbia.1993.

[7]李 惠，周文松，欧进萍，等.大型桥梁结构智能健康监测系统集成技术研究[J].土木工程学报，2006，39(2)：46-52.

[8]何旭辉.南京长江大桥结构健康监测及其关键技术研究[D].江苏：中南大学，2004.

[9]力宏男.结构健康检测[M].大连：大连理工大学出版社，2005.

[10]晏文渊.模态分析及信号处理在桥梁监测中的应用[D].陕西：长安大学，2011.

[11]Ebrahim Mehrani，Ashraf Ayoub，Amir A youb.Evalua-tion of fiber optic sensors for remote health monitoring of bridge structures[J].Materials and structures，2009(42)：183-199.