非局部薄板动力学特性分析的广义有限积分变换方法 *

姜人伟，杨树涛，赵佳敏，李道奎，马维力

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073； 2. 中国运载火箭技术研究院 北京宇航系统工程研究所， 北京 100076；3. 中南大学 土木工程学院， 湖南 长沙 410075)

薄板作为工程中应用最广泛的结构之一，其理论诞生以来就一直受到学者们的广泛关注。由于薄板的静、动力学控制方程均为高阶偏微分方程[1]，因此国内外大量学者都致力于研究其求解方法，例如Ritz法[2-3]、Navier法、Galerkin法及广义变分原理法[4]等，这些方法大多具有一定的局限性，仅能求解特定的问题，不具有普适性，直到有限元方法的产生[5]，才彻底解决复杂薄板问题的求解方法。

随着学者们的研究不断深入，研究对象也已经从宏观领域拓展到纳米领域，例如碳纳米管[6]和石墨烯板[7]。该类对象的研究手段主要有三种途径：实验方法、分子动力学方法和连续介质力学方法。实验方法是能够获得结构力学特性最直接、最有效的方法，类如Jena等[8]、Xu等[9]皆通过实验方法获得了石墨烯的剪切特性、弹性模量、屈服强度等参数，但实验方法投入大、成本高，经济性较差。分子动力学方法是一种理论数值仿真手段，其能够较好地获得纳米结构原子运动轨迹的微观细节，进而得到想要获得的特性参数[10]，但其缺点也较明显，即计算量大，即使是在计算机技术已经非常先进的今天，也仍难以对其进行快速的计算。相比于上述两种方法，连续介质力学方法具有计算效率高、计算结果相对较准确等优点，因此其被广泛应用于纳米结构的力学行为分析中。

学者们研究发现，适用于宏观尺度的经典连续介质力学方法，由于纳米尺度材料的尺度效应，往往得不到理想的结果[11]。此时，Eringen提出了应力梯度非局部连续介质力学理论[12]，该理论认为，物体中任一点的应力不仅与该点的应变有关，而且与其邻域内所有点的应变皆有关，因此其能够很好地考虑尺度效应。基于该理论，学者们对纳米结构的力学行为做出了大量研究[13-16]。但同时，由于非局部理论中非局部应力梯度项的引入，导致系统的能量泛函难以给出显示表达式，给控制方程的求解带来了一定的困难。

广义有限积分变换方法为求解线性偏微分方程的重要方法[17]，钟阳等[18-19]将其引入了弹性矩形薄板问题的求解中，并得到了理想的效果。该方法直接从控制方程出发，通过广义有限积分变换将高阶偏微分方程变换为线性方程组，进而得到待求解问题的精确解。因此，广义有限积分变换方法对求解非局部问题具有较好的适应性。

本文旨在推导基于应力梯度非局部薄板振动特性分析的广义有限积分变换方法，并将计算结果与有限元法及已有文献的结果进行对比，验证了本文推导的正确性。在此基础上，又研究了非局部参数、薄板的尺度对系统固有频率的影响。

1 非局部薄板动力学控制方程

与传统弹性理论不同，非局部弹性理论认为物体中任一点的应力不仅与该点的应变有关，而且与其邻域内所有点的应变皆有关。因此，在非局部弹性理论中，薄板的应力应变关系可以表示为

(1)

基于式(1)，考虑一个长为a，宽为b，厚度为h的矩形薄板，其动力学控制方程可以写成

(2)

其中：ρ为薄板的材料密度；D=Eh3/12×(1-ν2)为薄板的弯曲刚度，E为薄板的弹性模量，ν为薄板的泊松比。

对于四边固支边界条件，可以表示为

(3)

2 广义有限积分变换求解方法

为了求解式(2)与式(3)，定义二维广义积分变换对

(4)

其中，Xm(x)和Yn(y)为适应边界条件式(3)的积分核函数，即

(5)

为满足式(5)，Xm(x)和Yn(y)可取

(6)

其中，αm和βn分别需要满足

(7)

cm和cn分别定义为

(8)

此时，积分核函数Xm(x)和Yn(y)具有以下性质

(9)

对于控制方程(2)，设其解为

w(x,y,t)=W(x,y)sin(ωt+φ)

(10)

因此，控制方程(2)可改写成

(11)

对式(11)中的每一项做广义积分变换，并进行分部积分并化简，可得

(12)

其中，Imr、Ins、Jmr及Jns的表达式为

(13)

将广义积分变换后的结果式(12)代入控制方程(11)，可以得到

(14)

整理式(14)，并改写成矩阵形式，可得

(15)

其中

(16)

(17)

由于式(15)中W11、W12、…、Wtt不可能同时为零，因此式(15)成立的前提需要满足行列式

(18)

式(18)中仅含有未知变量ω，通过求解该式，即可得到薄板的固有频率。令非局部参数μ=0，上述求解过程即简化为宏观尺度下经典弹性薄板理论的广义有限积分变换求解方法。

3 结果分析

3.1 正确性验证

为了验证本文推导的正确性，将本文计算方法结果与有限元法或已有文献结果进行对比。首先，令非局部参数μ=0，将广义有限积分变换法的计算结果与有限元方法计算结果进行对比，计算过程中取薄板的几何参数及材料参数如下：边长a=b=1 m，厚度h=0.005 m，密度ρ=2 700 kg/m3，弹性模量E=7.2×1010Pa，泊松比ν=0.33。计算结果对比见表1，计算中广义有限积分变换法所取截断项数为4，即t=4，可见本文所采用的广义有限积分变换法的计算结果介于10×10单元和50×50单元的有限元法之间，这说明截断项数为4的广义有限积分变换法的计算精度要高于10×10单元的有限元法，同时这也验证了本文方法计算的正确性。

考虑纳米尺度的非局部薄板，其几何尺寸为：a=15 nm，a/b=1.5，厚度h=0.34 nm，密度ρ=2.25 g/cm3，弹性模量E=1.06 TPa，泊松比ν=0.25。在本算例中，固有频率ωk将通过式(19)无量纲化。

(19)

将计算结果与文献[14]中的算例结果进行对比，如表2所示。由表2可知，在取不同的非局部参数μ时，本文方法与已有文献中的结果吻合良好，进而也验证了本文计算方法的正确性。

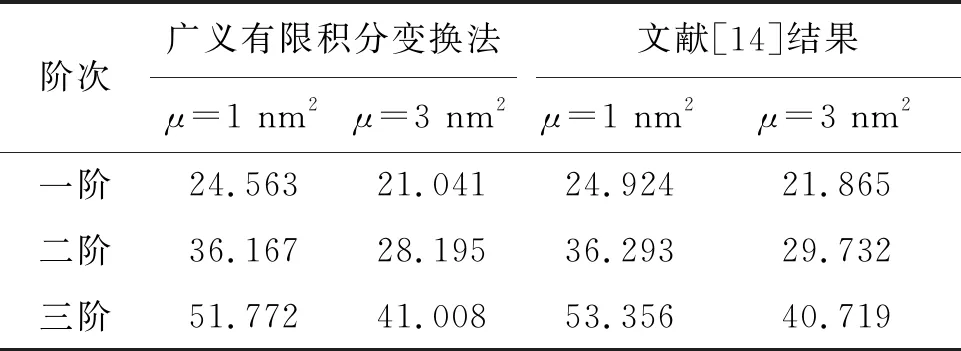
表2 不同非局部参数下固有频率计算结果对比

3.2 参数影响分析

3.2.1 非局部参数对固有频率的影响

图1 固有频率随非局部参数变化规律Fig.1 Nonlocal parameter effects on the nature frequency

3.2.2 薄板尺度对固有频率的影响

图2与图3分别给出了不同非局部参数下固有频率比随板的边长变化规律和不同阶模态随板边长的变化规律。在该算例中采用方形板，即a/b=1，厚度、密度及弹性模量等参数与之前算例相同。固有频率比的定义如下：

(20)

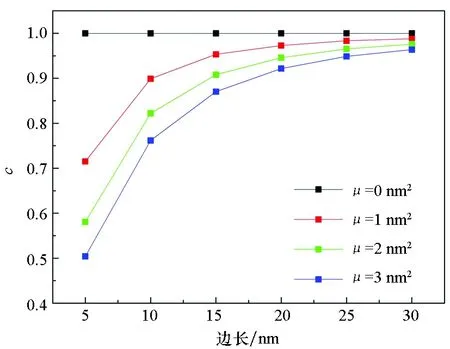
图2 不同非局部参数下固有频率比随板的边长变化规律Fig.2 Dimension effects on the nature frequency for different nonlocal parameters

图3 不同阶固有频率比随板的边长变化规律(μ=2 nm2)Fig.3 Dimension effects on the nature frequency for different mode (μ=2 nm2)

从图2中可以看出，随着薄板边长的增大，非局部理论结果逐渐靠近经典薄板理论计算结果，这也从侧面说明了非局部理论在纳米尺度下对薄板的固有频率影响较大，但到了宏观尺度下则可以不考虑非局部效应，采用经典的弹性薄板理论对结构进行分析即可。从图3中可以看出，高阶模态的固有频率比要小于低阶模态的固有频率比，该结论与文献[20-21]中的结论相同，这也从另一个角度验证了计算的正确性。

4 结论

针对应力梯度非局部薄板理论模型，推导了非局部薄板动力学特性求解的广义有限积分变换方法，得到了非局部薄板的固有频率，并将计算结果与有限元法及已有文献的结果进行对比，验证了本文方法的正确性。在此基础上，研究了非局部参数、薄板的尺度对系统固有频率的影响。主要结论如下：

1)广义有限积分变换方法直接对非局部理论控制方程进行积分变换，进而对控制方程进行求解，该方法可为难以写出能量泛函的高阶偏微分方程提供新的求解思路。

2)非局部参数的增大，薄板的固有频率会减小，随着模态阶次的增高，其受非局部参数的影响也逐渐增大。

3)在纳米尺度结构分析时需要考虑非局部效应，在宏观尺度下则无须考虑。