电磁发射超高速弹丸气动特性数值分析 *

冯军红，鲁军勇，李 开，李湘平

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

电磁发射超高速弹丸是指利用电磁能技术发射一体化弹丸至超高速状态，其具有初速高(可达6Ma以上)、射程远(可达200 km以上)、威力大以及发射能量精确可调等优势，是一种先进的动能杀伤武器[1-3]。作为大空域飞行的超高速弹丸，其气动减阻以及飞行稳定特性是关键，值得深入研究。随着计算流体力学的发展，采用数值方法计算超高速弹丸的气动力及力矩逐渐被国内外学者普遍接受，成为研究弹丸气动特性的重要手段[4-9]。

相对于传统的低速弹丸，超高速弹丸的飞行空域和速域范围较大，几乎覆盖了大气层的不同层段，涉及稠密大气层减阻、稀薄气体效应以及黏性干扰效应等气动现象，使得超高速弹丸气动力、力矩以及压心变化较大，存在大空域气动减阻、气动热防护和飞行稳定性等诸多问题。近年来，国内南京理工大学等[9-10]单位开展了超高速弹丸的气动特性研究，重点分析了弹丸的气动力和气动热特性，但缺乏对弹丸再入飞行段大攻角下的气动特性分析。其他研究单位也较少涉及这一方面的研究。

本文以电磁发射超高速弹丸为研究对象，采用雷诺平均数值方法计算了超高速弹丸的三维气动流场，并通过风洞试验数据验证了数值计算精度。重点分析了超高速弹丸再入段大攻角下的气动特性，得到了弹丸的非线性气动参数，为超高速弹丸再入段飞行稳定性研究提供了气动数据，也为弹丸外形设计提供了参考。

1 数值仿真方法

1.1 控制方程

不考虑体积力，采用Favre平均定常张量形式的N-S方程为：

(1)

(2)

(3)

1.2 湍流模型

对于弹丸的外部流场计算，最为常用的湍流模型是S-A(Spalart-Allmaras)单方程模型，详细的模型说明可见文献[11]。但是S-A湍流模型在预测分离流方面误差较大，石磊等[12]对比分析了S-A和k-ωSST湍流模型在预测高速旋转弹丸气动特性的精度，指出SST湍流模型在可压缩分离流预测方面优于S-A模型。SST湍流模型适合用于高速流动和由于逆压梯度造成的分流流动[13]，并得到了广泛的应用[9,14]，有关k-ωSST湍流模型的详细说明可见文献[15]。本文拟采用这两种湍流模型计算超高速弹丸的三维流场，并将计算结果与风洞试验进行对比，同时，采用k-ωSST湍流模型计算超高速弹丸再入段大攻角下的气动流场。

1.3 计算模型及网格

为减小气动阻力，采用无翼式布局，流线型外形，见图1。以弹丸总长L为特征长度，弹丸长细比约为7，尾翼呈“×”型结构，翼厚度为2 mm，斜置安装于弹丸底部。由于尾翼斜置的原因，使得弹丸并不完全对称，因此，建立了三维全弹模型，同时考虑超声速来流，前场流场区域为0.5倍弹长，后场区域为3倍弹长，径向为1.5倍弹长。采用ICEM CFD软件进行网格划分，在弹丸和尾翼壁面处进行网格加密处理，保证壁面y+值位于30～35之间，网格过渡比为1.2，如图1所示。

(a) 计算模型及对称面网格(a) Calculation model and grid of symmetry plane

(b) 三维网格结构(b) Three-dimensional grid (c) 尾部剖面网格(c) Tail section grid图1 计算模型及网格示意图Fig.1 Computation model and grids distribution

利用有限体积法、基于隐式方法数值求解定常的N-S方程，空间上采用二阶迎风格式进行离散，采用AUSM+通量分裂格式，弹丸和弹翼表面采用无滑移的绝热壁面条件，在来流入口、出口以及周向边界上均采用压力远场边界条件。整个计算工况见表1。基准工况的大气压力为101 325 Pa，温度为288.15 K，再入工况可取12 km海拔高度的大气参数，大气压力为19 399 Pa，温度为216.65 K。

表1 计算工况

2 计算结果分析

2.1 数值验证

2.1.1 网格无关性验证

为验证计算网格无关性，在现有模型基础上划分了3套不同数量的网格，网格加密方式相同，在弹体壁面附近进行网格加密，粗网格数量为160万，最小网格尺寸为0.05 mm，最大网格尺寸为4 mm；适中网格数量为260万，最小网格尺寸为0.02 mm，最大网格尺寸为1.5 mm；精细网格数量为330万，最小网格尺寸为0.01 mm，最大网格尺寸为1 mm。数值计算结果可见表2，升力系数的相对误差较小。俯仰力矩系数的相对误差从210万加密到330万时计算结果相差0.06%，这说明网格影响趋于收敛，本文选用适中网格数量满足计算要求。

表2 网格无关性数值验证

2.1.2 数值结果试验验证

采用风洞试验数据验证数值仿真结果，图2～4显示了数值计算和风洞试验的对比结果，分别对比了高马赫数下S-A和k-ωSST湍流模型的预测精度。可看出，法向力系数和俯仰力矩系数吻合较好，最大误差为1.8%。同时两种湍流模型的预测精度相当。相对于S-A湍流模型，k-ωSST湍流模型的最大误差为1.7%，略高于S-A模型的预测精度，这是因为法向力系数与俯仰力矩系数主要由气体压差产生，黏性项贡献较小，而两种湍流模型对压力项预测精度较高，所以误差较小。

图2 轴向力系数随攻角变化曲线(Ma=4)Fig.2 Variation curve of axial force coefficient with angle of attack (Ma=4)

针对轴向力系数，两种湍流模型的预测精度较低，尤其是k-ωSST湍流模型，最大误差达到14%，而S-A湍流模型的最大误差为4.7%。这是由于相对于法向力系数，轴向力系数的黏性项贡献较大，而湍流涡黏模型在预测湍流黏性项方面的误差较大，使得计算结果偏差较大。而S-A模型在计算外流场方面具有优势，因此得到了广泛的应用。但k-ωSST模型在计算分离流方面更具有优势[12-15]。因此，本文在基准工况下采用S-A模型；在再入工况下，由于弹丸攻角较大，会产生分离流，采用k-ωSST湍流模型进行计算。

图3 法向力系数随攻角变化曲线(Ma=4)Fig.3 Variation curve of normal force coefficient with angle of attack (Ma=4)

图4 俯仰力矩系数随攻角变化曲线(Ma=4)Fig.4 Variation curve of pitching moment coefficient with angle of attack (Ma=4)

2.2 基准工况气动分析

采用S-A湍流模型的计算结果分析了弹丸气动流场特性。图5显示了攻角3°工况下，不同截面的流场压力分布云图。图5(a)表示0°截面，即弹体的铅垂面，图5(b)表示45°截面，即绕弹中心轴旋转45°的截面。来流在弹体头部以及弹翼前缘形成脱体激波，但由于弹丸钝角较小，脱体激波距离较小。激波向周围空间延伸，且强度逐渐降低。针对高马赫数来流工况，来流激波角较小，使得激波后的气流贴近物体壁面。气流经过弹丸底部先膨胀后压缩，即底部流场除了由于高速气流引射作用形成的低压回流区外，还会形成再压缩波或激波，流场总压进一步损失。

(a) 0° 截面(a) 0° section

(b) 45° 截面(b) 45° section图5 不同截面的流场压力分布云图(基准工况)Fig.5 Pressure contour in different cross sections (base case)

对于超高速弹丸，气动阻力主要由三部分组成，即摩擦阻力、波系阻力以及底部阻力。从图5中可清楚看出波系阻力和底部阻力的产生机理。波系阻力主要是由于气流经过激波后总压损失，而底部阻力是由于弹丸底部低压造成的。图6显示了不同攻角下升力系数和阻力系数的变化曲线。升力系数随攻角接近于线性增长，而阻力系数随攻角的增长规律呈非线性。

图6 升力系数和阻力系数随攻角变化曲线Fig.6 Variation curve of lift and drag coefficient with angle of attack

图7 压心系数和升阻比随攻角变化曲线Fig.7 Variation curve of pressure center coefficient and lift drag ratio with angle of attack

图7显示了弹丸压心系数和升阻比随攻角的变化曲线。随攻角的逐渐增大，弹丸的压心系数逐渐变小，说明弹丸的静稳定裕度降低，在大攻角下，弹丸的稳定性变差，不利于弹丸姿态收敛。此外，升阻比随攻角先增大后减小，从图6也可看出，升力系数和阻力系数增长趋势不同，在大攻角下，阻力系数增长更快，而升力系数相对较慢，导致升阻比增长逐渐变小，存在极值，针对本文研究的弹丸，在Ma=4工况下，攻角在12°左右，升阻比达到最大值。这是因为在大攻角下，气体流动分离导致诱导阻力急剧增大，使得总阻力增大，最终导致升阻比达到极值，这也符合升阻比变化规律。

2.3 再入工况气动分析

重点分析了再入工况下弹丸在大攻角下的气动特性。图8显示了攻角25°下，不同截面的流场压力分布云图(图8(a)和图8(b)的截面定义与图5相同)。大攻角下，气体横向效应比较明显，弹丸迎风面这一侧的激波强度较大，激波后的静压急剧增大，而弹丸的背风面由于气流的分离作用使得压力逐渐减小。相对于低攻角工况，流场的波系结构对弹丸的影响比重较大，使得弹丸的气动阻力和升力均增大。

(a) 0°截面(a) 0° section

(b) 45°截面(b) 45° section图8 不同截面的流场压力分布云图(再入工况)Fig.8 Pressure contour in different cross sections (reentry case)

图9对比了攻角3°和攻角25°两种工况下的底部流场结构。在小攻角下，弹丸来流边界层未发生分离现象，底部回流区相对对称，而在大攻角下，由于弹丸背风面的边界层分离与再附作用，使得来流较为复杂，回流区呈现更为复杂的形态，存在滑移线，形成剪切层。这些流场形态均会影响弹丸的气动特性和飞行稳定性。

(a) 3° 攻角(a) 3° angle of attack

(b) 25°攻角(b) 25° angle of attack图9 弹丸底部流场速度分布云图Fig.9 Velocity distribution of flow field at the base of projectile

图10 流向截面的压力分布云图(再入工况)Fig.10 Pressure distribution in streamwise section (reentry case)

由于弹丸在大攻角下横流效应明显，这里详细分析了流向截面的压力分布和流向涡结构分布。图10显示了靠近弹丸尾部流向截面的压力分布云图，可明显看出经过激波后的流场压力突增，类似于乘波结构，而在弹丸的背风面，由于分离作用弹丸表面压力较小，使得弹丸上下压差较大，形成气动升力。图11对比了不同攻角下的流向涡结构，重点分析横流绕过弹丸表面后，在背风面的气流形态，可看出，在小攻角下，气体横向流速较小，基本贴体流动；而在大攻角下，横向气流绕过弹体后形成脱落涡结构及一对清晰的流向涡，流向涡导致弹丸背风面形成低压回流区，使得压力降低。由此可知，大攻角下弹丸的迎风面气动流场类似于乘波结构，弹丸的背风面流场类似于低压脱落涡结构。这两种流场机理均对弹丸的气动特性存在影响。

(a) 3° 攻角(a) 3° angle of attack

(b) 25° 攻角(b) 25° angle of attack图11 不同攻角流向截面的流向涡分布云图Fig.11 Streamwise vortex distribution in different streamwise sections

图12 弹丸表面压力系数流向变化曲线Fig.12 Pressure coefficient curve on projectile surface

为进一步分析这两种机理对弹丸气动特性的影响效果，分析了弹丸表面的压力系数变化规律，如图12所示。气流经过弹丸头部后，由于激波作用，压力系数急剧降低，随后流经迎风面的气流压力系数逐渐减小，而背风面的气流压力系数变化较小，在靠近尾翼处，由于尾翼的影响，使得压力系数产生突变。对比不同攻角的压力系数变化，可看出，随攻角的增大，迎风面的压力系数变化较大，而背风面的压力系数变化相对较小，这说明迎风面的波系结构、流场特性对弹丸的气动特性影响更为显著。

图13显示了再入工况下(Ma=2)弹丸阻力系数和压心系数随攻角变化曲线。随着弹丸攻角的增大，阻力系数迅速增大，尤其是攻角大于15°后，弹丸的阻力系数增长较快，这说明了大攻角下阻力系数的非线性特性。同时，弹丸的压心系数也逐渐减小，当攻角大于15°后，由于弹丸压心系数的前移，使得静稳定裕度降低了4.5%，这说明再入工况下，弹丸的再入攻角较大，使得弹丸气动阻力迅速增大，静稳定裕度急剧降低，弹丸的姿态收敛较慢，从而使弹丸再入段的速度衰减较大。

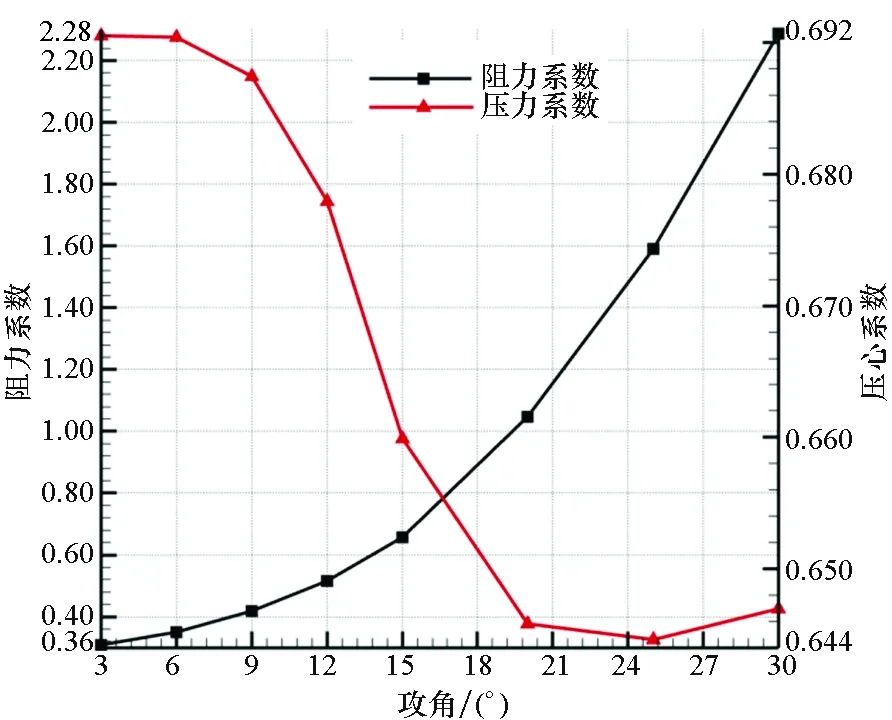
图13 阻力系数和压心系数随攻角变化曲线(再入工况)Fig.13 Drag coefficient and pressure center coefficient change with angle of attack (reentry case)

弹丸的阻力系数是攻角的偶函数，略去四阶以上微分项，可写为：

(4)

(5)

式中，ΔCD=(CDj-CD(j-1))/(αj-αj-1)，Δα=αj-αj-1。计算结果见表3。初步评估在大攻角工况下，弹丸的阻力二阶项是小攻角的2倍，这说明在大攻角下，阻力系数二阶项或诱导阻力是弹丸气动阻力的主要组成部分。

弹丸升力系数是攻角的奇函数，略去高阶项，可得：

(6)

可采用一阶差分格式评估弹丸气动升力的非线性特性。计算公式为：

(7)

计算结果可见表3。在小攻角工况下，ΔCL/Δα的值较小，且基本相同，这说明升力系数随攻角的线性变化特性；在大攻角下，ΔCL/Δα的值是小攻角的2倍，这说明一阶线性近似误差较大，而且随着攻角的逐渐增大，ΔCL/Δα值逐渐增大，这说明大攻角下弹丸升力系数的非线性特性，高阶项的比重逐渐增大，需要引入更高阶量才能更为准确地计算气动参数。

表3 气动系数与攻角的差分量

3 结论

采用数值计算方法研究了超高速弹丸的气动流场特性。利用风洞试验数据对比了两种湍流模型对超高速弹丸气动数据的预测能力，计算结果表明两种湍流模型在计算法向力和俯仰力矩系数等方面的预测精度较高，可达到2%以内，而在阻力系数预测方面，精度较差，S-A湍流模型的预测精度达到4.6%，而k-ωSST湍流模型的预测精度达到14%，这说明S-A湍流模型在预测弹丸外流场特性方面具有较高的精度，这与先前的研究结果一致。

分析了弹丸的底部和横向流场分布特性。相对于小攻角的气动流场，大攻角的弹丸底部流场更为复杂，回流区存在滑移线等非定常流场结构。大攻角下的弹丸横流效应更为明显，使得高速流场在弹丸背风面形成对称的脱落流向涡，这些流向涡导致弹丸背风面的压力降低。在迎风面，激波效应较为明显，激波后压力急剧增大，类似于乘波结构，而迎风面的压力变化对弹丸的气动阻力和升力特性贡献作用更大。

最后，分析了弹丸气动非线性特性，在大攻角下，弹丸的气动升力和阻力系数呈现明显的非线性特性，阻力系数明显增大，而且弹丸的静稳定裕度也急剧降低，使得弹丸的收敛特性变差，这是引起弹丸再入段速度衰减的主要原因。