运用动态规划的智能卫星集群星间通信路由算法 *

伦伟成，李 群，于芹章，张 灿

(1. 国防科技大学 系统工程学院, 湖南 长沙 410073； 2. 复杂系统仿真总体重点实验室, 北京 100101)

智能卫星是具有自主能力的一类人造卫星，它能够在尽可能减少地面指令的直接操控下独立完成任务，如此可降低操作成本且节省通信资源。单个智能卫星的能力有限，将多个智能卫星编组为智能卫星集群(Smart-Satellites-Swarm，SSS)则可以增强卫星的多任务遂行能力和抗干扰能力，提高卫星完成复杂航天任务的效率和成功率。以色列的SAMSON计划[1]和美国的小行星探测计划[2]都是典型的智能卫星集群实例。

要促进从智能卫星的“单体自主”向SSS的“群体智能”发展，必须使卫星具备网络化信息协同能力，在此基础上建立有效的星间信息协同机制，让SSS的成员卫星可以借助星间链路进行通信以实现信息交互和任务协作，从而更好地完成那些对时效性、响应性、自主性都有较高要求的任务。为了达到前述目标，亟待解决智能卫星集群的星间通信路由问题(Inter-satellite Communication Routing Problem of Smart-satellites-swarm，ICRPS)。ICRPS的核心是如何规划数据从源卫星传到目的卫星的合理路径，使星间通信在时延等方面满足任务要求。

星间通信路由问题可以在卫星网络的背景下进行研究，卫星网络的节点是卫星、边是星间链路。Xu等[3]提出了基于编码的多路径路由算法以应对多层卫星网络中的通信拥塞问题。Xie等[4]面向动态星间网络提出了采用广义领域搜索的星间路由算法。Huang等[5]采用梯级优化设计方法来设计导航卫星网络的星间链路联络方案。Wang等[6]面向低轨卫星通信网络提出了基于软件定义网络架构的改进路由算法。尤启迪等[7]针对面向卫星网络的空间信息快速回传场景提出了多路径快照聚合路由算法。Soret等[8]面向低轨元星座卫星网络提出了通过最小化轨道面间链路来自动分配路由的算法。Zhang等[9]面向低轨卫星网络提出了基于星间链路状态信息的星上自动控制的路由算法。Roth等[10]针对双低轨Walker星型星座设计了采用星间链路的两层地理路由体制。梁俊等[11]针对软件定义卫星网络提出了基于切比雪夫神经网络的智能路由策略。

上述算法主要针对传统卫星，在工作模式方面还是由地面的指控中枢预先规划路由，且路由一旦确定便不再更改，卫星在其中只能机械地收发数据，若将这些算法用于ICRPS，则无法发挥智能卫星的自主性优势。

因此本文研究了一种适用于智能卫星的星间通信路由算法，该算法基于动态规划的思想，由各卫星自主参与规划路由，使其在规划时能够根据SSS现状灵活调整路由，达到路由在数据传送过程中持续动态更新的效果。

1 ICRPS概述

为了求解ICRPS，需要基于SSS建立智能卫星集群网络(Network of Smart-Satellites-Swarm，NSSS)：将SSS各成员抽象为节点，成员之间存在的星间链路抽象为边，边的权值就是星间链路的长度；从而把ICRPS转换为求解NSSS的两个节点间的最优路径。

不过，ICRPS寻求的最优路径要满足时延最短而非长度最短。时延是指数据从源卫星传送到目的卫星所需的时间，ICRPS主要考虑以下两种时延：

1)发送时延，指从发送数据的第一个比特算起到其最后一个比特发送完毕所需的时间[12]，等于数据长度与发送速率之商；

2)传播时延[12]，指电信号传播星间链路长度的距离所需的时间，等于星间链路长度与电信号传播速率(约等于光速)之商。

因NSSS的节点处在不断运动中，节点间时延和链路连通性也在不断发生变化[11]，故NSSS其实属于动态网络；但在某个具体时刻NSSS又是静态网络，因为卫星在此时刻的位置是固定的。考虑到NSSS的这种二元特性，结合智能卫星的自主性，采用动态规划策略求解ICRPS，分多个阶段规划SSS成员星间通信的路由，在每一阶段中把NSSS作静态网络处理，各阶段的NSSS整合起来又是随时间变化的动态网络。

采用图论的表示方法[13]，将NSSS记作(V,A)，V表示节点集(即卫星集合)，A表示边集(即星间链路集合)，节点数记为|V|=n，再构造NSSS的邻接矩阵Q=(qij)n×n，qij的赋值规则如式(1)所示。

(1)

为便于表达，规定：卫星vi、节点vi和vi这三种表达是等价的；边和星间链路含义相通；边权值和星间链路长度含义相通。

包含vi和vj的卫星对能否建立星间链路(简称“建链”)取决于是否同时满足以下两个条件：

1)卫星对彼此可见，要求地心到卫星对连线的直线距离hL大于地球强电离层高度hI与地球半径RE之和，即

hL>hI+RE

(2)

2)卫星对可以互相通信，要求vi对于vj的俯仰角θi在vi的天线扫描范围之内且vj对于vi的俯仰角θj在vj的天线扫描范围之内，即

(3)

式中，γi,min和γj,min分别表示vi和vj的天线扫描范围的下限，γi,max和γj,max表示上限。

卫星对若能建链，便可以进行通信，此时其星间链路的长度就等于卫星之间的直线距离。

作为智能卫星，SSS各成员可以采用文献[14]中的方法根据轨道根数计算其他成员在惯性坐标系的位置，进而在考察是否满足式(2)和式(3)所示条件的基础上得到当前时刻的NSSS。在必要时，SSS将通过地面站上注星历等方式保证计算的准确性。

2 星间通信路由静态规划算法

2.1 算法描述

星间通信路由静态规划算法借鉴了Dijkstra算法[15]的思想，用于求解某一具体时刻的静态NSSS上一条以vb为起点、ve为终点的时延最短路径。

设vi,vj∈V，定义有向链表Pj(vi)表示从vj到vi的路径(未必最优)，Pj(vi)的长度记作Lj(vi)，Pj(vi)的节点数记作|Pj(vi)|，从而构造函数Tj(vi)描述数据传输的总时延：

(4)

式中，c是电信号在星间链路中的传播速度(下同)，dT表示数据的一次发送时延。则算法追求的最优即等价于Tb(ve)最小。

将vj到vi的最优路径的时延记作Dj(vi)，定义集合Sb表示为规划从vb出发的最优路径而考察过的所有节点。初始时，对∀vi∈V，令Pb(vi)=[vb,vi](采用中括号表示链表，以区别于集合)，Dj(vi)=0，Sb={vb}。算法的具体流程如算法1所示，其中运算符⊕表示将符号后的元素添加到符号前的链表末尾。

算法1 星间通信路由静态规划算法

2.2 算法有效性分析

本节将证明算法1的有效性。

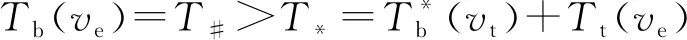
前述证明否定了算法结束时有vt∈Sb或vt∈V-Sb，于是vt∈∅，因此并不存在比P#更优的P*，从而推翻假设，证明算法1有效。

□

3 求解ICRPS的动态规划算法

3.1 基本算法描述

哥哥茫然地不知道说什么。这时祖父进来了。看了翠姨的热度，又感谢了我的母亲，对我哥哥的降临，感到荣幸。他说请我母亲放心吧，翠姨的病马上就会好的，好了就嫁过去。

因此，本节在算法1的基础上，设计一种基于动态规划求ICRPS可行解的算法2。考虑到智能卫星搭载的宇航级芯片的性能可达400 MIPS[16](今后还会变得更快)，则相比于传送时延，其路由规划的耗时可以忽略不计，所以卫星将其规划路由的具体时刻的NSSS作为静态网络处理而采用算法1推算其到目的卫星的路由(算法2第6至7行)。可见，采用算法2求出的路由具有时间属性，路由的每一段路径都是前驱卫星在其规划路由时刻到后继卫星的最优路径，这种最优是针对特定时刻的，不同的规划时刻可能会得到不同的最优路由。

算法2 求解ICRPS的动态规划算法

3.2 面向数据分段传送的算法扩展

受网络协议等因素的限制，星间链路一次传输的数据长度往往是有限的，过大的数据将被拆分为若干数据子段以时分复用的方式分别传送，而且两次传送之间还存在一个空时隙，所以卫星在发送每一个数据子段时都必须重新规划当前时刻的路由。

设需要一个长度为lT的数据从vb传送到ve，星间链路一次传输的最大数据长度为lm。考虑有lT/lm=p，p+1,…,lr，则需要将原数据拆分为p+1个数据子段(若lr=0则拆分为p个数据子段)，前p个数据子段长度为lm，第p+1个数据子段长度为lr。基于此，针对前述分段不连续传送的情况将算法2扩展为算法3。

算法3 面向数据分段传送的路由算法

4 ICRPS的仿真建模

4.1 智能卫星Agent的行为模型

在ICRPS的仿真中，一个仿真时刻要同时处理多个智能卫星诸如计算星间链路、收发数据、规划路由等多种行为。为此，采用基于Agent的建模与仿真(Agent-Based Modeling and Simulation，ABMS)方法[17]，建立智能卫星Agent(Smart Satellite Agent，SSA)模型，以刻画智能卫星的自主性与行为并发性。

在ICRPS仿真中，存在三种角色的SSA：源卫星、目的卫星、中转卫星。目的卫星只要接收其他卫星发送的数据即可。

图1 源卫星的行为流程Fig.1 Action process of source satellite

中转卫星vα的行为流程如图2所示。中转卫星通过设置中转任务列表(Transfer Task List，TTL)来处理多数据子段，每接收到一个数据子段便将其加入TTL中。TTL采用先进先出策略，若TTL非空，则调取排在第1位的数据子段为其规划路由从而将其发送出去。

在图2中，中转卫星也受规划有效时间ΔT′的约束，如果超过ΔT′仍不能建链，则数据传送中断，需要生成传送中断信息，然后以本星为源卫星、vb为目的卫星，采用算法3规划路由将传送中断信息反馈给vb，由vb根据任务时效性决定是否重新传送。如果中转卫星收到其他卫星发来的传送中断信息，将优先处理这些信息。当然，传送中断信息也面临传送失败的风险，必要时可以借助地面站来传送。

图2 中转卫星的行为流程Fig.2 Action process of relaying satellite

在Agent建模时，每一个SSA都被赋予上述三种角色的行为，在具体的仿真场景中各SSA根据自己被分配的角色而采取相应的行为。

4.2 ICRPS仿真的调度算法

算法4的关键是为SSA设置延迟。延迟是指实体停留在进程中的某一点不再向前移动，延迟结束时实体所在的位置就是复活点——进程继续推进的起点。延迟分为两类：无条件延迟是指预先确定延迟持续的时间，到时间后自动结束延迟；条件延迟是指事先无法确定何时结束延迟，必须等到满足某些条件后进程才能继续。例如空时隙属于无条件延迟，TTL为空时属于条件延迟。

5 仿真实验与分析

5.1 实验设计

选择体系效能分析仿真(System-of-systems Effectiveness Analysis Simulation，SEAS)平台来建立SSA模型，采用ABMS方法对ICRPS进行仿真实验。

算法4 SSA仿真调度算法

表1 SSS类型

取γi,min=γj,min=20°，γi,max=γj,max=60°[18]，hI=120 km[19]，RE=6 378.137 km。数据长度为2 048 000 bit，设星间链路一次传输的最大数据长度为51 200 bit，即源卫星需要分40次发送长度为51 200 bit的数据子段。卫星发送数据的速率为100 kbit/s，空时隙为0.1 s，规划有效时间ΔT′=1 min。仿真开始时刻为格林尼治时间2019年9月19日0时0分2秒，持续时间为2 min，步长为1 ms。

5.2 实验结果分析

5.2.1 实验结果分类

将ICRPS仿真实验可能出现的结果划分为图3所示分类树中实线框标识的7种类型，据此对10 620个实验结果进行分类，如表2所示。

图3 实验结果的分类树Fig.3 Classification tree of experiment results

可见，在相同的星间链路参数下不同SSS的实验结果并不相同。中轨卫星组成的SSS-3任意两个成员之间的数据传送都能够正点连续完成，没有任何推迟或中断，因为中轨卫星高度较大，姿态更加灵活，更易满足建立星间链路的条件。

表2 实验结果分类统计

SSS-1和SSS-2的实验结果绝大多数都全程无通路，因为其中包含的低轨卫星高度较低，很多情况下与其他低轨卫星或中轨卫星并不可见或无法通信，遂不能直接建链。事实上，在SSS-2中，甚至有20颗卫星(编号为6、8、9、11、19、20、22、23、30、31、33、34、42、44、45、47、55、56、58、59)与其他所有成员在2 min内都不能建链。

SSS-1的结果更能反映卫星轨道对星间路由的影响：870次正点连续传送都发生在中轨卫星之间；55次推迟连续发送和14次传送推迟后中断都在低轨卫星之间；2 601次全程无通路中没有一次发生在中轨卫星之间。

不过，图3中的“无法建链”仅表示从仿真开始后1 min以内无法建链，并不意味着卫星对之间永远不能建链，例如SSS-2的0号成员与3号成员在仿真开始后3.094 min才成功建链，超过了1 min的规划有效时间。

上述结果都是基于5.1节中的星间链路参数取值，并不是所有轨道类型的卫星在这些参数约束下都表现良好，hI、γi,min、γj,min、γi,max、γj,max、ΔT′等参数对低轨卫星的建链及规划结果的影响远大于对中轨卫星的影响。如何设置相关参数以避免出现数据传送失败及中断是一个重要的问题，仅在路由算法层面是不足以解决的，需要对卫星本身进行改进，例如增大卫星天线扫描范围[20]、卫星姿态机动、改变卫星星座构型甚至卫星轨道。这种改进需要符合实际，不能为了追求高效能而随意放宽约束。

5.2.2 路由跳数分布

10 620个实验中有5 109个卫星对完成全部40个数据子段的传送，因每个数据子段都对应一个路由，共得到204 360个有效路由，这些路由跳数的分布如图4所示。

(a) SSS-1

(b) SSS-2

(c) SSS-3图4 有效路由跳数分布直方图Fig.4 Histograms of normal routing hops

SSS-1和SSS-3的有效路由跳数分布在结构上相似，都是跳数为1和2的路由占绝大多数，在5.2.3节将介绍何时出现跳数为3的路由，而出现跳数大于1的路由则说明即使中轨卫星之间也会有无法直接通信的情况。

SSS-2的有效路由则出现了1到11这几种跳数，全部25 760个有效路由的跳数均值为3.683 54，跳数为1的路由只占14%。如前所述，低轨卫星较难直接建链，所以SSS-2成员之间直接通信的占比明显小于SSS-1和SSS-3，多数卫星对的星间通信还需通过中转卫星来完成。

5.2.3 路由的改变

按卫星对间传送不同数据子段的路由是否有变化可以对图3中的第2、3、5、6种结果类型分别进一步细分，如图5所示。

基于图5对表2中的部分实验结果进行二次分类，其结果如表3所示。表3中3-2型和6-2型的结果都不为零，说明采用算法3能够在星间通信中断的情况下重新恢复路由；而表3中3-1列和6-1列的结果都为零则表明不存在传送中断后恢复但路由不变的情况，因为中断前后的NSSS并不相同。

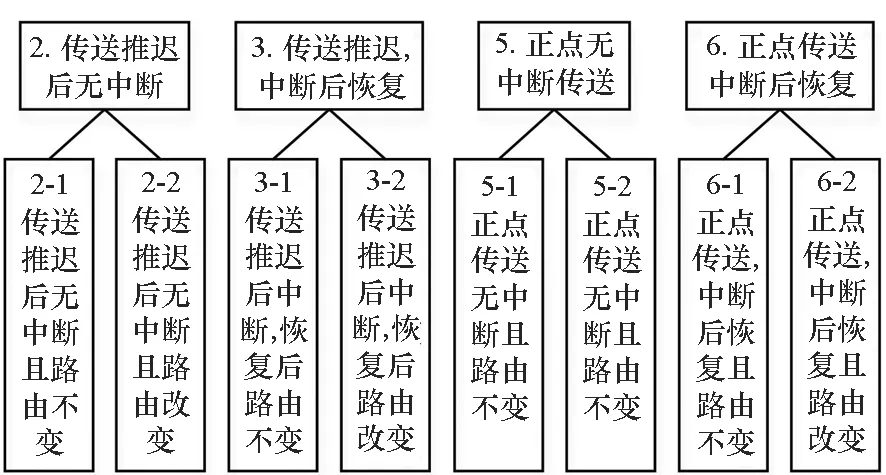
图5 实验结果的二次分类Fig.5 Further classifications of experiment results

表3 实验结果的二次分类统计

表3中路由改变的实验结果共计421个，它们的路由变化类型可以大致分为7种，如图6所示。类型1、2、3(图6中三者部分点线完全重合)见于SSS-1和SSS-3的中轨卫星对路由的变化。图4(a)和图4(c)中所有跳数为3的数据子段路由都出现在类型1所代表的卫星对路由中。类型3表示路由改变但跳数不变，仅见于跳数为2的路由。

图6 路由变化类型Fig.6 Types of routing changes

类型4、5、6、7(图6中类型6和类型7的部分点线完全重合)见于SSS-2的低轨卫星对的路由变化，其跳数有的由大变小(类型5)，有的由小变大(类型6、7)，还有先增后减(类型4)。类型7是无中断传送的路由，其跳数变化幅度相对较小，而类型4、5、6都是中断后恢复的路由，其跳数变化幅度较大。

图7和图8分别展示了上述7种变化路由及不变路由(类型8)的狭义时延和广义时延。狭义时延是指发送时延与传输时延之和。广义时延是指狭义时延加上其他形式的时延，主要有两种：排队时延是指数据为等待排在其之前的数据都发送完而耗费的时间；中断时延是指数据等待中断的星间链路恢复而耗费的时间。如图7所示，狭义时延与跳数的变化趋势几乎一致，表明二者存在相关性。

图7 典型路由的狭义时延Fig.7 Simple delays of typical routings

图8 典型路由的广义时延Fig.8 General delays of typical routings

广义时延的变化如图8所示，呈现以下规律：

1)数据子段1的广义时延总等于狭义时延，此后随着数据子段序号增大，其广义时延一般会随之递增，因为越靠后的数据子段经历的排队时延越大，如类型2、8；

2)规律1建立在所有数据子段路由的前两个卫星(即源卫星及其后继卫星)都相同的前提下，若源卫星的后继卫星改变，则排队时延将从头算起，就会出现类型1、3所示的广义时延起伏变化的情况(图8中类型1的部分点线被类型2、3遮挡)；

3)相比于无中断传送时跳数增加对广义时延的影响(类型7)，中断时延对广义时延的影响程度更大，类型4、5、6的路由中断时延甚至超过了一些数据子段的广义时延。

路由变化的原因可以分为两类：

1)数据连续传送中存在时延更短的路由：包括类型1中跳数由3变为2、类型3中跳数由9变为7，及类型2的路由变化；

2)原星间链路失效，重新规划路由：包括类型2、5、6、7，及类型1中跳数由2变为3、类型3中跳数由6变为11。

不过，类型5所示的路由变化表明，原因2导致的路由变化并不必然使狭义时延增大，时延变短的路由变化也不一定是原因1造成的。

6 结论

本文在提出求解ICRPS的动态规划算法的基础上，结合智能卫星所特有的自主性，将智能卫星建模为Agent，并为基于智能卫星Agent的ICRPS仿真设计了调度算法。借助SEAS平台对三种SSS内部成员之间的路由进行了仿真实验，实验结果表明，本文研究的算法可以有效解决不同SSS下的路由问题。不过，对实验结果分析发现，路由规划的结果受到SSS体系架构和硬件层面因素的深刻影响，如SSS星座构型和卫星轨道，以及星间链路的数据传输能力等，如何优化这些因素以提升SSS的效能将是今后的重要研究方向。