改进的局部均值分解法在爆破振动去噪中的应用

郭航伸，郭连军,2，杨 巍，潘 博，徐振洋

(1.辽宁科技大学矿业工程学院，辽宁 鞍山 114051；2.沈阳工业大学建筑与土木工程学院，沈阳 110870；3.成远矿业开发股份有限公司，辽宁 辽阳 111000；4.北京科技大学土木与资源工程学院，北京 100083)

在爆破作业环境采集的振动信号通常会含有大量噪声信号，且噪声来源复杂多样。目前，常见的振动信号去噪方法有滤波法[1]、形态学法[2]、小波法[3-4]、经验模态分解法[5]等。但是这些方法的去噪效果一般且不易精确重构原始爆破振动信号。小波技术具有多分辨分析特性和良好的时频局部性，原始信号分解后，真实信号和噪声可依据小波系数的不同特性实现分离，被广泛应用于爆破振动信号去噪领域[6-7]。局部均值分解法[8](LMD)是2005年由Jonathan Smith提出的一种自适应的信号时频分析方法，可以将一个复杂的非平稳信号分解成若干个PF(Product Function)分量和残余量之和的形式，每一个PF分量由其对应层的包络函数和纯调频函数相乘得到，所有PF分量的瞬时频率和瞬时幅值叠加便得到了原始信号完整的时频分布。LMD方法由于其良好的分析非线性、非平稳信号的能力，已在脑电信号分析[9-10]和机械故障诊断领域[11-12]得到应用。LMD法虽然比经验模态分解法更为温和，但同样存在模态混叠和端点效应问题[13]。

通过引入边界局部特征尺度匹配延拓算法[14]、自适应互补集合算法与小波阈值法对局部均值分解算法进行改进，以实现对爆破振动信号的有效降噪。

1 自适应互补集合局部均值分解算法

1.1 总体平均局部均值分解方法

总体平均局部均值分解方法[15]是对局部均值分解方法的改进，通过添加辅助噪声进行数据分析，向原始信号中添加n次等幅值随机白噪声后进行LMD分解，加入的白噪声使得数据极值点的分布更加均匀，进而改善了LMD算法中存在的模态混叠问题，同时利用多次随机白噪声的均值接近于0的特性消除引入白噪声的影响。

1.2 自适应互补集合局部均值分解算法

自适应互补集合局部均值分解算法(CELMDAN)是对ELMD算法的改进。ELMD算法中加入了多次白噪声，最终数据重构误差取决于加入白噪声的次数，次数越高则重构误差越小，但是程序的运行时间更长。CELMDAN算法通过添加有限次数的自适应白噪声，使信号能在加入较少次的噪声下达到重构误差为0，所以CELMDAN不但可以降低LMD算法中存在的模态混叠状态，还具有重构误差小，计算效率高的优点。其算法的具体流程如下：

在原始信号x(t)中加入N个不同的白噪声，进行LMD分解，对获得的PF分量取平均值，得到第1个模态分量，记为

(1)

第1个唯一的剩余分量记做r1(t)，记为

r1(t)=x(t)-PF1(t)

(2)

定义Ek(·)为信号经过LMD分解产生的第k个PF分量，则第2个模态分量如下

(3)

第k个剩余分量记为

rk(t)=rk-1(t)-PFk(t)

(4)

第k+1个模态分量记为

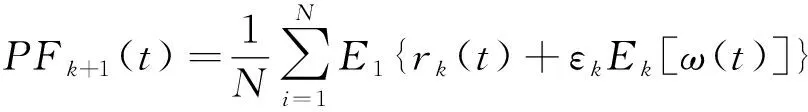
(5)

执行公式(4)和公式(5)，直到余量信号不能被分解时停止。分解终止时，信号可以表示为

(6)

式中：R(t)为最后的剩余分量。

从上述的算法中可以看出，CELMDAN的算法分解过程是完整的，能够对信号进行精确重构，且在分解的过程中能通过系数εk选择合适的噪声。

1.3 端点效应的处理方法

LMD算法也存在端点效应，算法中由于振动信号两侧的极值是未知的，在插值拟合的过程中会出现较大的误差，进而出现端点效应。针对LMD算法中的端点效应问题，相关学者提出了一些改进方法[16-17]。

边界局部特征尺度匹配延拓法可以有效地解决信号两端出现的端点效应。设Mi、Ni分别为信号的极大值和极小值，对应的时间点为tmi、tni，S1为信号左边界处的点。

首先以S1-M1-N1为三角形，找到3个顶点对应的时间坐标，找到S1对应的点Si，Si对应的时间点tsi由下式可得：

(7)

若求得的tsi不在原始信号的波形上，采用插值的方法求出Si。然后计算匹配误差Ei：

Ei=|Si-S1|+|Ni-N1|+|Mi-M1|

+|Mi+1-M2|

(8)

当min(Ei)<βl时，认为信号的规律性较强。其中β为常数，β取值既不能太大，也不能太小；l为S1-M1-N1构成的三角形数据长度。若计算出的匹配误差在所规定的阈值内，取所有计算出的匹配误差中的最小值；当计算出的匹配误差有两个或两个以上时，取与起始点距离最远的波形。当匹配误差不满足条件范围时，则认为信号规律性不强。此时根据信号的端点极值点的特征进行延拓，对信号的另一端采用同样的方法进行计算，两侧的计算完成后，就可以采用完成后的数据进行分解。以上过程可以看出，经过延拓方法处理的数据与原始信号具有很好的一致性。

2 小波阈值降噪方法

在爆破振动信号去噪中，小波阈值去噪有较为广泛的应用。小波阈值去噪方法是将爆破振动的时域信号转换到小波域，在小波域进行阈值处理。由于随机噪声具有较小的小波系数，可以设置相应的阈值将其去除，再把处理后的剩余信号重构，可以获得去噪后的信号。小波阈值去噪效果的优劣与所选的小波基、分解层数、阈值估计方法和阈值函数有关。阈值选取法主要包括默认法、硬阈值法和软阈值法，默认法适应性差，可信度较低；硬阈值保留较大的小波系数，能够保留信号有效部分的特征；软阈值将大于阈值的系数向零收缩，去噪效果更为平滑。软阈值的具体处理过程如下：

(9)

式中：xs(i,j)为去噪后的小波系数；x(i,j)为去噪前的小波系数；thr(i)是由各类阈值准则确定的阈值。

3 基于CELMDAN和小波阈值的降噪方法

单独使用小波阈值降噪方法虽然能够消除爆破振动信号的噪声，但是同时也消除了一部分有用信息。单独使用CELMDAN对爆破振动信号进行强制降噪时，通常的做法是直接去除前几个PF分量，这样虽然去掉了高频噪声，但是前几个PF分量也包含了爆破振动信号内在的高频信息。为了最大程度去除信号噪声同时尽可能保留信号中的有用信息，提出基于CELMDAN和小波阈值相结合的降噪方法。

首先采用CELMDAN算法将爆破振动信号分解为一系列的PF分量，然后分别计算各PF分量的自相关系数，根据自相关系数判断包含随机噪声的PF分量，对由噪声主导的PF分量利用小波阈值降噪方法进行降噪处理，最后将小波阈值降噪后的PF分量与剩余PF分量重构得到降噪后的爆破振动信号。

4 仿真分析

对提出的基于CELMDAN和小波阈值去噪方法进行仿真测试。测试中，采用两组正余弦波相加来模拟爆破振动信号，两组正余弦波分别为2sin (100πt)和cos (50πt)，频率分别为50 Hz和25 Hz，采样频率为2 048 Hz，采样时间为2 s(见图1)。在仿真信号数据中加入信噪比(SNR)为2的白噪声，得到假设的含噪爆破振动信号(见图2)。

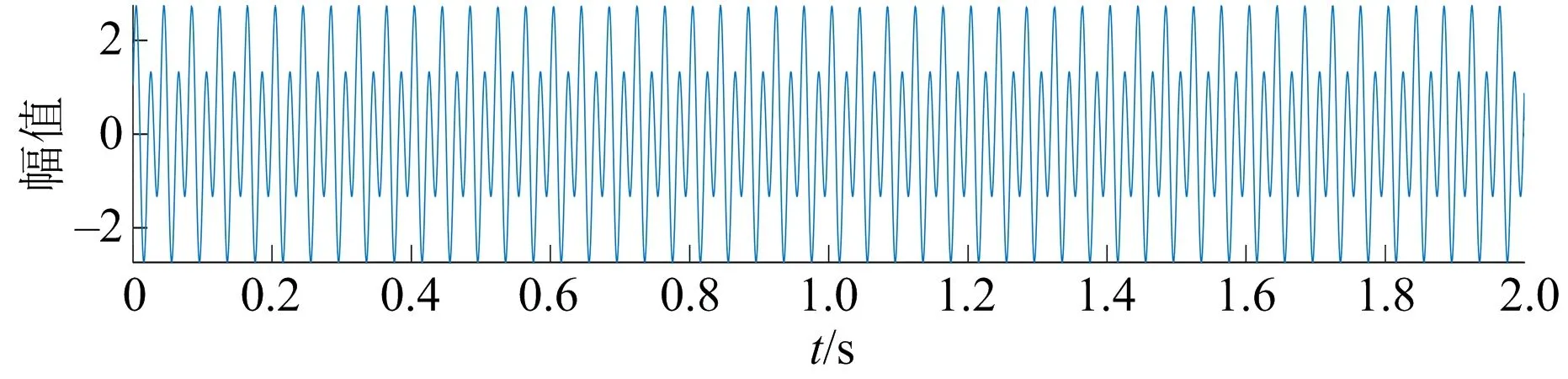
图1 仿真信号Fig.1 Original signal

图2 含噪仿真信号Fig.2 Vibration signal containing noise

将含噪仿真爆破振动信号进行CELMDAN分解，共得到11个PF分量以及1个趋势项，PF分量如图3所示。分别计算各个PF分量的自相关系数，当某个PF的自相关系数较小时，则认为该分量的主要成分为噪声，将判断为噪声PF分量再进行小波阈值降噪处理。降噪后的结果如图4所示。

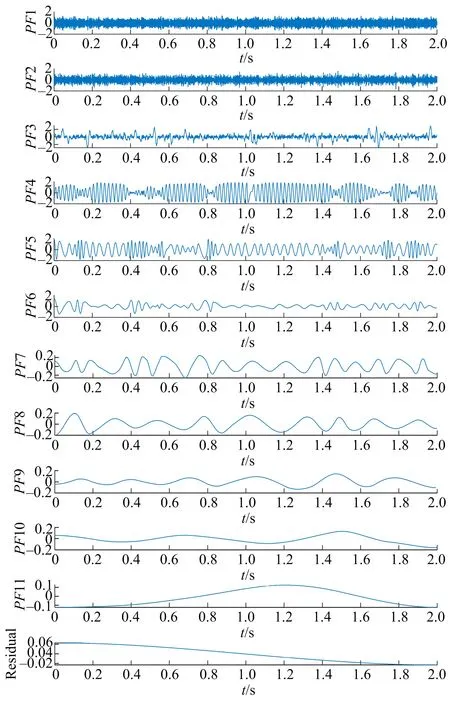
图3 CELMDAN分解结果Fig.3 CELMDAN decomposition results

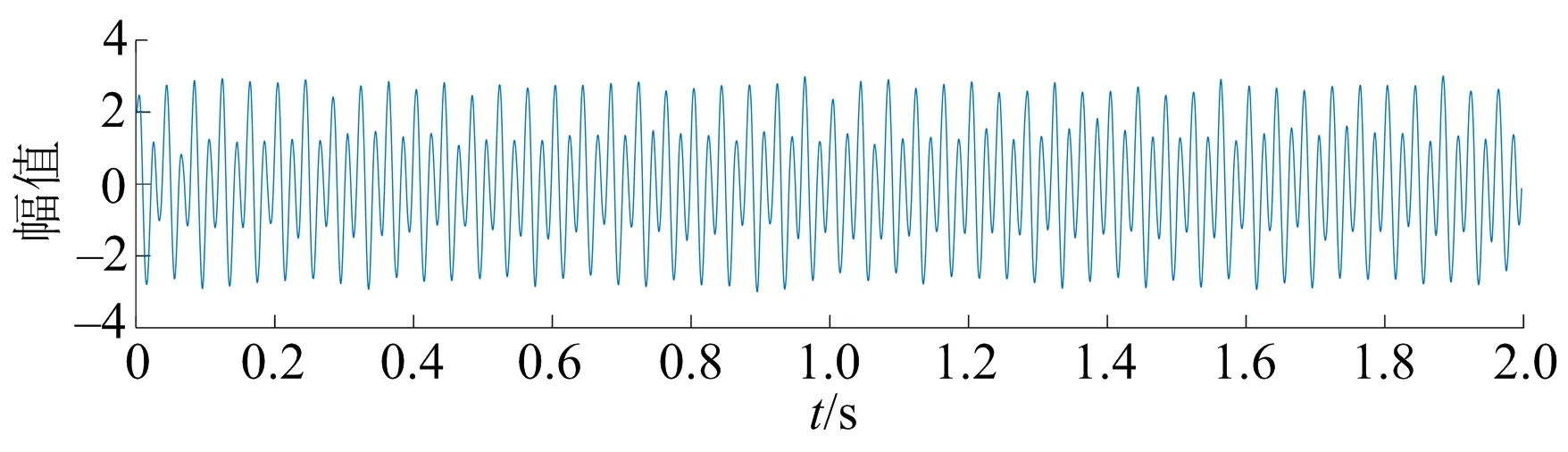
图4 降噪后信号Fig.4 Signal after noise reduction

为验证CELMDAN-WT方法对比其他方法的优势，分别采用小波阈值直接降噪方法、EMD分解、ELMD分解去除第1个分量降噪法对仿真信号降噪处理。采用均方根误差(RMSE)和信噪比(SNR)两项指标对算法的性能进行检验，均方根误差和信噪比定义如下[18]：

(10)

(11)

表1 不同去噪方法的性能

对比4种方法的性能指标可以得出：单独使用小波阈值去噪方法在去除噪声时也带来严重的信号失真；EMD分解后单独舍弃IMF1分量，由于噪声信号去除不完全，导致信噪比不高，信号局部不光滑；总体平均局部均值分解和经验模态分解相比较而言，一定程度上降低了模态混叠现象，去除了更多的噪声，相比于前两种方法信噪比提升很大；而采用CELMDAN-WT去噪方法处理信号时可以得到更高的信噪比和更小的均方根误差，信号获得了良好的降噪效果。

5 应用实例

以某工程现场实测爆破振动信号为例，爆破振动信号来自鞍钢关宝山露天铁矿爆破现场，该区域地质条件较差，测点周边临近省道、村庄、民房，由于测试环境复杂，获取的爆破振动信号受噪声污染严重。监测仪器为成都中科测控有限公司生产的TC-4850测振仪，测量范围：0～35 cm/s；A/D分辨率：16 Bit；频响范围：0～10 kHz；测量精度：0.01 cm/s。随机选取了在不同时间内测得的两组数据进行处理，原始数据如图5所示。原始爆破振动信号波形复杂、受噪声污染严重，需要去噪处理获得真实信号。采用CELMDAN-WT方法对所测信号进行去噪处理，去噪后信号如图6所示。

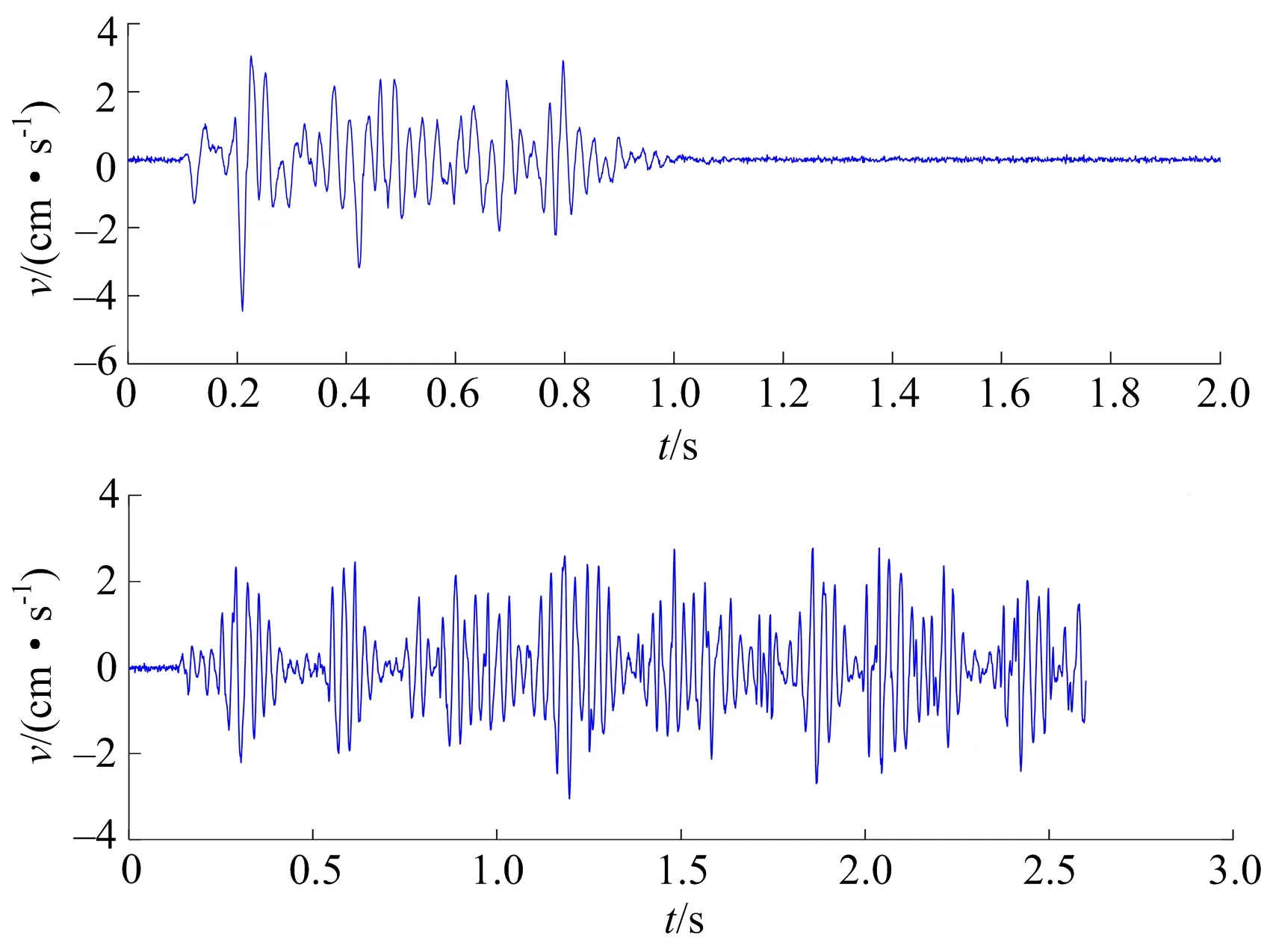
图5 现场监测原始信号Fig.5 Signals measured in situ

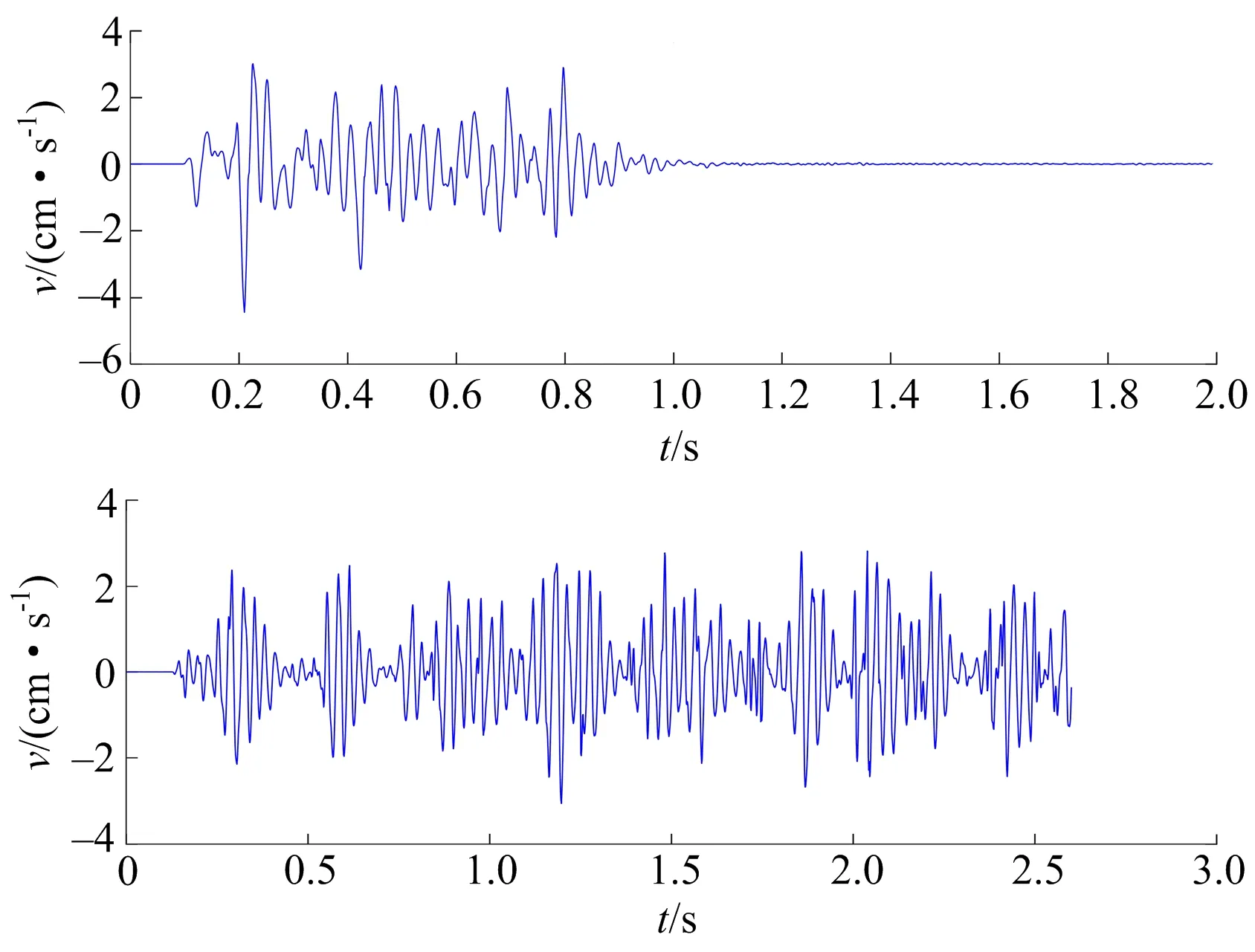
图6 去噪后信号Fig.6 Denoised signal

由图6可以明显看出，经过CELMDAN-WT方法去噪后的爆破振动信号波形较去噪前清晰，计算含噪爆破振动信号去噪后的信噪比、均方根误差，计算结果如表2所示。

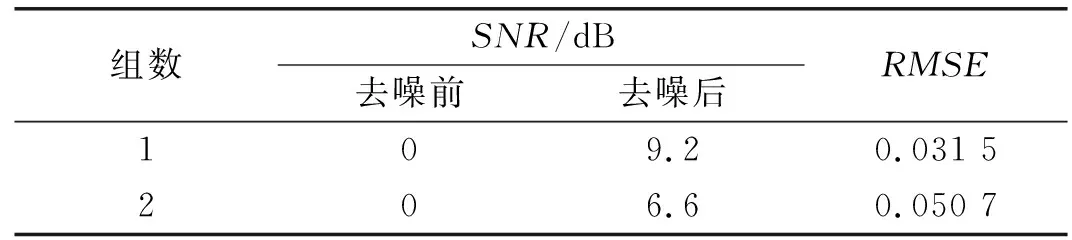
表2 爆破振动信号去噪效果

从表2中可以看出，去噪后爆破振动信号的信噪比都有不同程度的提升，受噪声干扰最严重的是第1组信号，信噪比提升了9.2 dB。对去噪前后的信号做FFT时频谱分析，去噪前后频域如图7所示。

图7 去噪前后信号频域Fig.7 Frequency domain of signal before and after denoising

从图7可以看出，原始含噪信号的频谱相对杂乱。100 Hz以下的低频部分是爆破振动的优势频段，但其在频谱图中优势不明显，说明信号受到了严重的噪声干扰，经过去噪处理后的信号频谱优势频段更加明显。经过CELMDAN-WT方法处理后的爆破振动信号，信噪比有了较大的提升，信号的原始信息得到了更好的保留，为下一步的爆破振动信号的分析提供了可信的基础。

由原始爆破振动信号三维能量(见图8)可以看出，爆破振动信号能量主要集中在0～100 Hz，在100～200 Hz范围内分布着大量的低能量信号，这些低能量信号主要是采样环境中的其他噪声信号。通过与采用CELMDAN-WT方法去噪后爆破振动信号的三维能量(见图9)，对比可以看出，原始爆破振动信号经过去噪后，100～200 Hz内噪声信号基本完全除去。由于噪声信号的存在，信号优势频段在三维能量图中表现不明显，而去噪后则可以明显看出信号有用成分能量在时域和频域的分布。

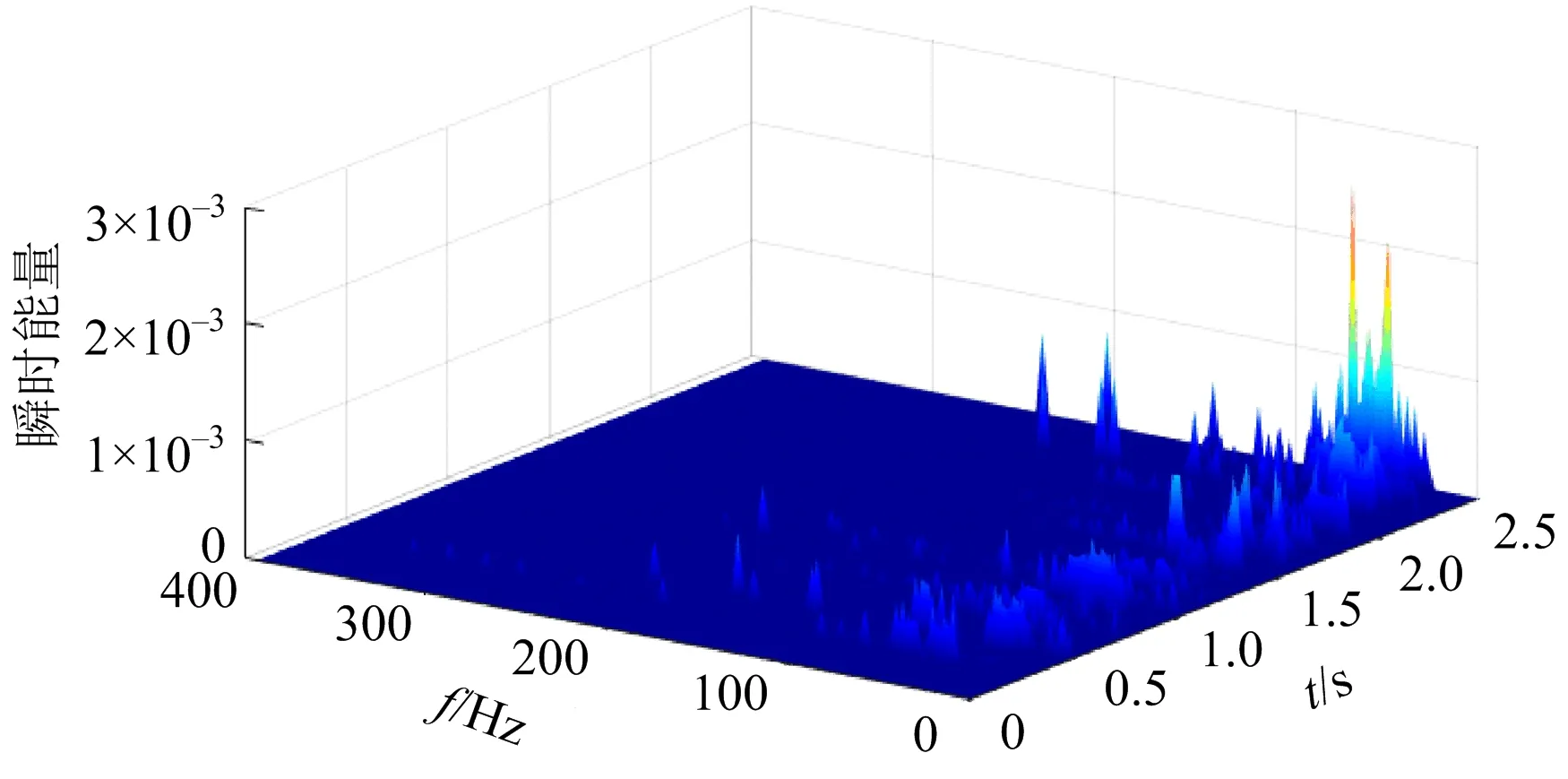
图8 原始爆破振动信号三维能量Fig.8 Three dimensional energy of original blasting vibration signal

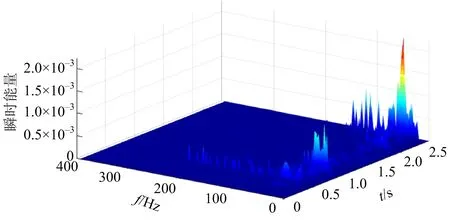
图9 去噪后爆破振动信号三维能量Fig.9 Three dimensional energy of blasting vibration signal after denoising

6 结论

1)对含有噪声的爆破振动信号直接使用小波阈值法降噪效果不佳，信号严重失真。

2)EMD和ELMD方法分解后直接剔除IMF1分量虽然能够去除一部分噪声，但因为存在模态混叠的问题会减少信号高频部分的有用成分。

3)CELMDAN-WT方法能够有效地消除爆破振动信号中的噪声，实现了信号与噪声的分离，信噪比最高提升9.2 dB。