爆破振动对高层框架-剪力墙结构的影响

李 猛，范延静，李 彬，潘建荣，王 湛

(华南理工大学土木与交通学院，广州 510641)

随着爆破技术的广泛应用，爆破施工带来的危害也越来越受到关注[1]，特别是爆破地震波产生的爆破振动，它会对附近正在建或者已建成的建筑物产生损伤破坏[2-5]。因此，研究爆破地震波对建筑物的影响具有重要意义。

目前，关于爆破地震波的研究主要包括爆破振动传播规律以及临近建筑物的动力响应。对于爆破振动传播规律的研究，前苏联学者M.A.萨道夫斯基通过对大量爆破数据进行分析，并结合相似原理，提出了萨道夫斯基公式，该公式在我国被广泛应用于爆破振动分析[6]。然而，经典萨道夫斯基公式未考虑高程对振动速度的影响，使其应用范围存在局限性。针对萨道夫斯基公式的不足，Marrara等[7],崔未伟等[8]对高程影响峰值速度进行研究，并指出峰值振动速度随高差增加而增大。谭文辉[9]、郭得福等[10]通过量纲分析的方法，得到了考虑高程差的振速预测公式。随着对爆破振动研究的深入，爆破地震波作用下建筑物的动态响应成为研究热点之一。

雷振等[11]对爆破地震波作用下不同建筑高程振动规律进行探究，研究表明在测点同一楼层时，水平距离不变，随着距地高差的增加，振动速度也越来越大。P.K.Singh等[12]研究不同起爆方式、爆破孔径等相关爆破参数对结构的影响。罗艺等[13]，王松青等[14]，曹孝君[15]考虑了爆破地震波主频对结构物的影响，研究表明振动速度的放大作用不仅与高程有关，还与爆破地震波主频、振动传播历程等因素有关。但目前的研究集中于结构整体振动频率与爆破地震波频率的关系，而对于结构建筑内部构件振动速度局部放大效应研究存在不足。

本文结合广东以色列理工学院二期校区山体爆破工程，采用爆破振动记录仪对建筑周边基础和建筑结构内部进行监测。通过对振动数据进行线性回归分析，确定结构内部振动频率对结构局部振动放大效应的影响，从而探究爆破冲击波的传播规律以及爆破作用下高层建筑内部结构构件振动规律。通过研究建筑物振速与地基振速放大倍数的比值关系，可估计框架-剪力墙结构不同构件处振速，提出建筑结构中易破坏位置选取原则，对类似爆破工程安全施工起指导作用。

1 工程实例

1.1 工程概况

广东以色列理工学院二期校区位于广东省汕头市金平区，校区南侧山体存在大量土石方需要爆破。校区内教师宿舍BC栋临近爆破山体，且施工工期与山体爆破时间相重合，为确保结构构件及施工安全，需要对结构关键构件采用施工监测。BC栋建筑为框架-剪力墙结构，高37.05 m，共12层。山体主要为燕山期花岗岩，采用延时起爆方式，相邻药包起爆时间间隔为75 ms。爆源单排布置，一排6个钻孔，孔径90 mm，孔深约8 m，孔距3 m，最大单段装药量144 kg，单孔药量约24 kg。

1.2 测点布置

为研究爆破冲击波振动传播规律，采用JM-3874三向加速度传感器对距离爆破点不同位置处地表振速进行监测。在此基础上，为探究爆破对建筑结构内部构件的影响，根据建筑构件距爆破点距离的不同以及迎爆面的位置，采用JM-3874三向加速度传感器对C栋建筑关键构件振速进行监测。

在距爆破点140、150、200、240、290 m处设置A～E共5个地表监测点(见图1)，采用全站仪测量其x、y、z坐标。

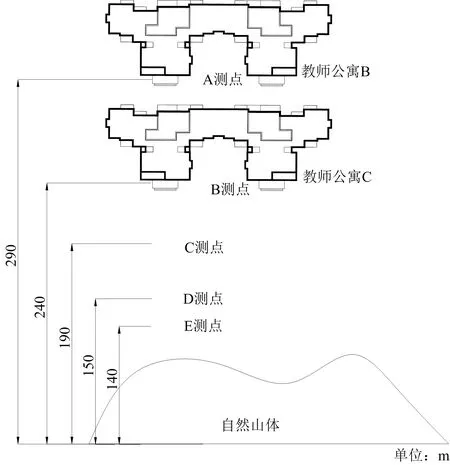
图1 地表测点布置Fig.1 Layout of surface measuring points

C栋中测点布置如图2所示，此时爆破点距C栋建筑水平距离为340 m。测点编号按照测点方位：W(西侧)、E(东侧)、C(中部)，结合测点前后顺序，所在楼层数混合编号。具体测点编号分布如图2所示。

注：E1-1-柱子；E2-1-工具间；W1-1-窗台；W2-1-窗台；C1-1-窗台；C2-1-楼板；E1-6-阳台；E2-6-阳台；W1-6-阳台；W2-6-柱子；C1-6-窗台；C2-6-楼板；E1-12-阳台；E2-12-卫生间；W1-12-窗台；W2-12-柱子；C1-12-窗台；C2-12-楼板。

2 爆破振动监测结果与分析

2.1 振速随爆心距变化规律分析

地表测点测得的x、y、z方向峰值振动速度如表1所示。

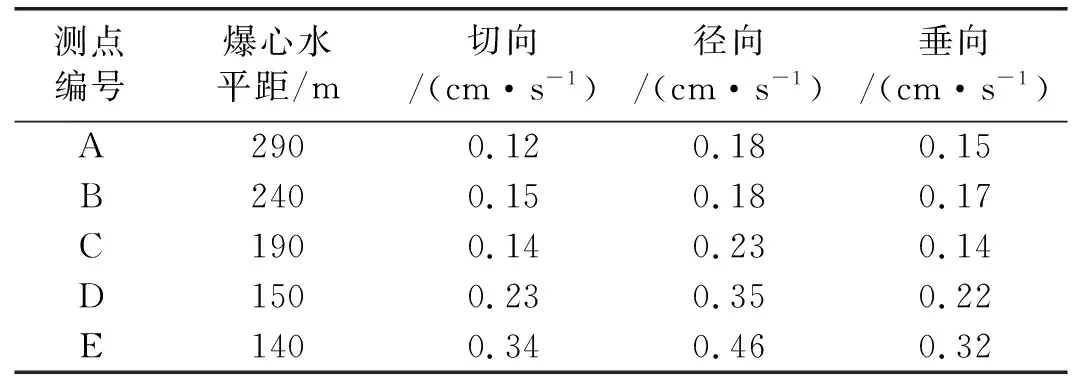
表1 地表测点振动数据

根据表1得到地表测点爆破振动速度随距爆破点水平距离的变化趋势如图3所示。

图3 地表测点振速随爆心距变化Fig.3 Change of vibration velocity of ground measuring points with the distance between blasting centers

由图3可知，随着距爆破点水平距离的增加，切向、径向和垂向振速逐渐减小且衰减趋势相同：距爆破点距离近时，振速衰减较快；距爆破点距离远时，振速基本无衰减。同时，地表测点径向振速大于切向和垂向速度。

为判断地表测点振速是否合理以及分析爆破地震波传播规律，对爆破振动质点速度采用萨道夫斯基公式进行回归分析。由于监测测点位于地表平面与爆破作业爆源点的高程差相对较小，所以不考虑高程差的影响。本文参考文献[6]所采用的萨道夫斯基模对振速进行拟合，其表达式如下：

(1)

式中：v为测点x、y、z方向最大振动速度，cm/s；Q为最大段药量，kg；R为爆源至测点的水平距离，m；K、α为与地质特征相关的系数。

按照最小二乘法原理，对振动数据进行回归分析，得拟合结果如图4所示。其线性回归系数r2为0.879，大于0.85，表明本文拟合结果较好，能真实反映测点振动速度数据。通过拟合公式计算得K=26.05,α=1.28，由此可得该区域爆破地震波峰值振速衰减公式，如式(2)所示。

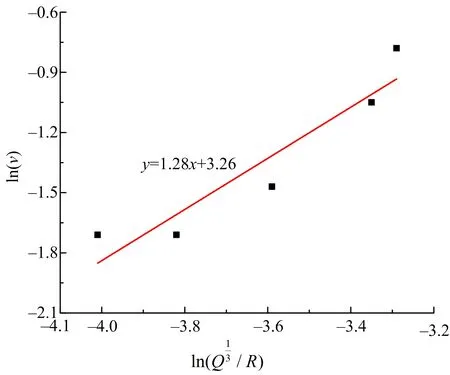
图4 地表测点振速回归分析Fig.4 Regression analysis of vibration velocity of ground measuring points

(2)

2.2 结构振动速度规律分析

地表测点峰值速度对应主振频率如表2所示。

表2 地表测点主振频率

为了研究结构构件振速与地基频率的关系，参考文献[16]可得爆破振动主频预测公式为

(3)

式中：f为爆破振动主频预测值，Hz；Kf、γ为与地质特征相关的系数。

按照最小二乘法原理，对振动数据进行回归分析。线性回归系数r2为0.954，表明爆破振动主频预测公式拟合较好，测点主频数据较为可靠，Kf=18.65,r=—1.697 1，由此可得该区域爆破地震波主频预测公式：

(4)

由式4可得，当监测点布置在C栋内部时，C栋地基频率为f=8.6 Hz。建筑内部测点振动峰值速度及主振频率如表3所示。

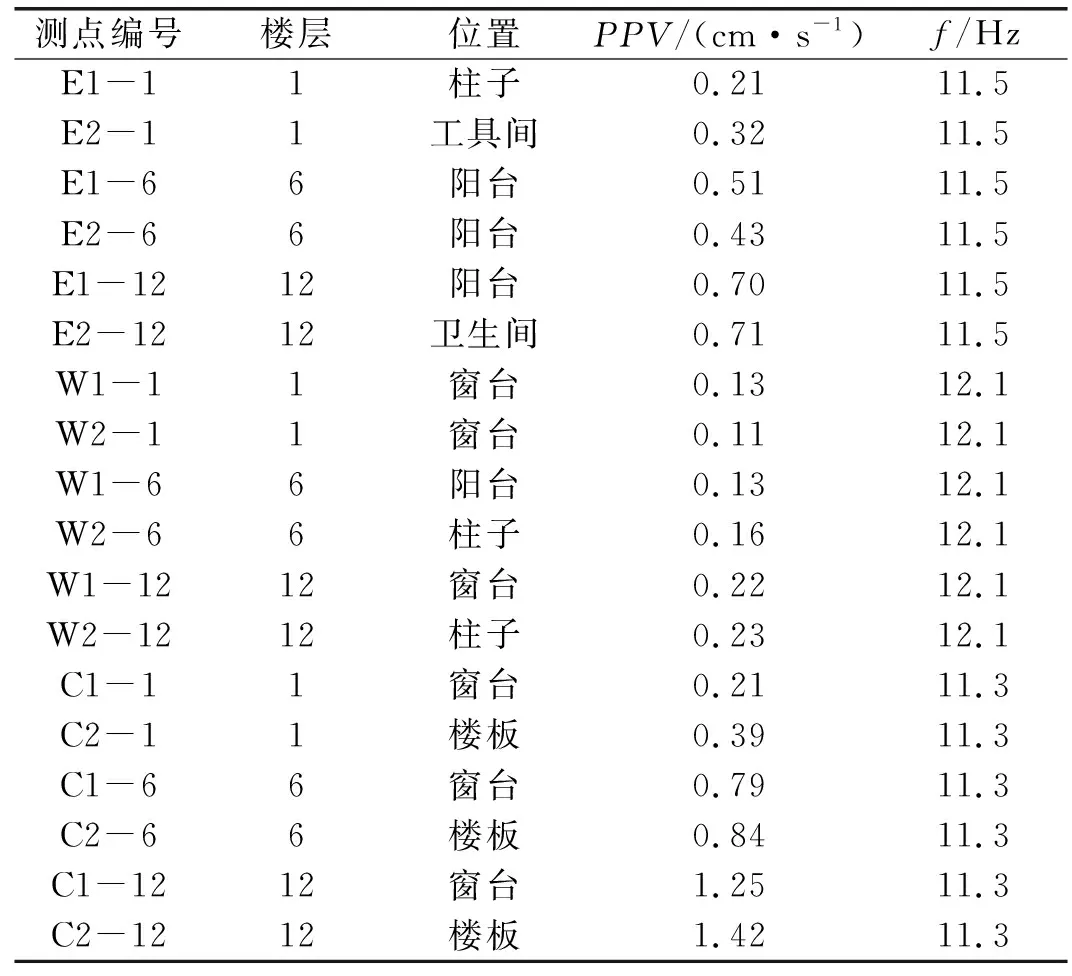
表3 结构内部测点峰值振速及频率

由于爆破荷载为非周期荷载，可采用主振频率表示为结构构件自振频率，其仅与自身的质量和刚度有关。故在实际监测中，C栋建筑的东侧、西侧和中间结构质量和刚度的差异使得结构自振频率不同，在监测的建筑主体和各局部构件引发的振动各不相同。为探究结构自身振动响应与频率的关系。定义λ为频比系数，即局部结构监测的主振频率和地基主振频率的比值：

(5)

式中：fw为地基础主频，Hz；fc为局部结构振动主频，Hz。

对同一楼层、相同频率结构局部振速取合速度，得到结构局部振速相比于地基速度的放大倍数和不同高程、频比系数的关系如表4所示。振速放大倍数随距地高程变化如图5所示。

表4 结构局部峰值振速与高程、频比系数的关系

图5 振速放大倍数随距地高程变化Fig.5 Magnification of vibration velocity varies with the elevation above ground

由图5可知，在频比系数相同的情况下，随着距地高程的增加，振速放大倍数逐渐增大；在距地高程相同的情况下，随着频比系数的减小，振速放大倍数明显增大。在本次框架-剪力墙结构监测结果表明：在同一频比系数下，框架-剪力墙结构随着距地高差的增加，振速放大倍数呈线性增长。而随着频比系数的减小，线性系数值也增大，在频比系数为1.41时，建筑高度增加16 m，振速放大倍数平均增大35%；在频比系数为1.34时，建筑高度增加16 m，振速放大倍数平均增大150%；在频比系数为1.31时，建筑高度增加16 m，振速放大倍数平均增大400%。在频比系数增加量相同的情况下，随距地高程的增加，振速放大倍数增加量逐渐增大。频比系数增大0.01，在距地高程0.4、16.4、34.4 m时，振速放大倍数增大0.1、1.0、1.8倍。

3 结论

1)爆破振动作用下地表质点各向峰值振速随爆心距的增大而减小，各点径向振动速度大于垂向和切向速度。

2)随着距爆破点水平距离的增加，地表质点x、y、z方向的振速逐渐减小，其速度衰减趋势相同：距离爆源较近的区域，地表质点振速衰减较快，距离爆源较远的区域，地表质点振速衰减较慢。

3)结构内部振速存在局部放大效应。在同一频比系数下，随着距地高程的增加，振速放大倍数呈线性增长，随着频比系数的减小，线性增长系数值也增大，建筑高度增加16 m，在频比系数为1.41、1.34、1.31时，振速放大倍数平均增大0.35、1.5、4倍。

4) 多层框架-剪力墙结构在爆破地震波作用下，在频比系数增加量相同的情况下，随距地高程的增加，振速放大倍数增加量逐渐增大。频比系数每增大0.01，在距地高程0.4、16.4、34.4 m时，其振速放大倍速增大0.1、1.0、1.8倍。中部顶层楼板结构在距地34.4 m、频比系数为1.31时，振速放大倍数约为10倍，应对此处进行重点监测，必要时可采取减少爆破炸药量、建筑物周围开挖减振沟等方式实现减振效果。