基于PSO优化LS－SVM的电力现货市场价格预测＊

张睿，杨瑞，董海雷，谭江浩

（广州汇电云联互联网科技有限公司，广东 广州 510000）

随着电力体制改革浪潮的推进，电力现货市场是当下电力工业发展的必然趋势[1－2]。目前我国电力现货市场处于摸索阶段，市场规则、电价和报价机制还不成熟，在市场环境下，电力现货市场价格的准确预测有利于发电企业开展报价决策工作[3]，因此对电力现货市场价格预测具有重要意义。

目前电价预测方法主要有时间序列法、灰色预测法、神经网络法和组合预测法等。文献[4]考虑到电价的时间特性，采用自回归移动平均模型（Autoregressive Moving Average，ARMA）对次日电价进行了预测，并对预测模型进行了误差修正。文献[5]为了提高电力现货市场电价预测精度，对传统灰色模型进行改进，采用改进灰色模型预测了电力现货与中长期市场价格。文献[6]考虑了现货市场与长期合约市场之间的关系，建立了一个改进的多电价格灰色模型来综合预测这两个市场的价格；并采用灰色求解优化算法，充分利用数据的各个信息，提高了预测精度。文献[7]将集成经验模态分解、支持向量机和自回归移动平均模型相结合，建立了电价组合预测模型，并采用电力市场的实际电价数据验证了模型的正确性。上述文献虽然基于不同的方法建立了电价预测模型，但电价预测精度有待进一步提高。

综上所述，为了提高电价预测精度，本文采用粒子群优化算法（（Particle Swarm Optimization，PSO））对最小二乘支持向量机（Least Squares Support Vector Machine，LS－SVM）的惩罚因子和径向基核函数宽度进行优化，建立基于PSO优化LS－SVM的电力现货市场价格预测模型，采用算例分析验证本文提出电价预测方法的正确性和模型的实用性。

1 最小二乘支持向量机

最小二乘支持向量机是Suykens基于支持向量机（Support Vector Machine，SVM）提出的一种改进方法，它与SVM具有相同的核函数，LS－SVM回归过程中同样遵循结构风险最小化原则。LS－SVM与SVM不同点在于优化指标和约束条件，LS－SVM的优化指标采用平方项，约束条件采用等式约束，其优点是在不影响回归精度的情况下大大减少了计算量。相比于神经网络，LS－SVM结构简单，回归拟合精度更高，目前在交通、金融和电力行业应用广泛[8]。

2 粒子群优化算法

粒子群优化算法是由Kennedy等人根据自然界中飞鸟群搜索食物的行为提出的一种优化算法，空中飞鸟在搜索食物时，需要相互竞争也要相互合作才能找到食物，飞鸟相当于粒子，而食物就相当于数学问题的最优解[10]。PSO算法原理简单、参数较少，在回归算法的参数寻优中得到了广泛应用。

PSO算法的原理如下[11]：令D维空间中种群为X＝（x1，x2，L，x）n，其中 n 为粒子个数。则第 i个粒子的位置向量为Xi＝（xi1，xi2，L，xi）lT，速度向量为Vi＝（vi1，vi2，L，vi）lT，令粒子群中个体极值为Pi＝（pi1，pi2，L，pi）lT，种群极值为Pg＝（pg1，pg2，L，pg）lT。粒子每经过一次迭代，则更新各自的速度和位置，速度和位置更新公式为：

3 基于PSO优化LS－SVM的电力现货市场价格预测模型

3．1 模型的建立

相比于神经网络，LS－SVM不易陷入局部最优，回归拟合效果更好，但LS－SVM的拟合精度受惩罚因子C和径向基核函数宽度σ影响较大，为了提高电价预测精度，本文采用PSO算法对LS－SVM的C和σ进行优化，建立基于PSO优化LS－SVM的电力现货市场价格预测模型，具体建模步骤流程如图1所示，建模步骤如下：

图1 建模流程图

1）数据归一化。为了减小数据之间的影响，需对模型的输入数据进行归一化处理，公式如下：

式（14）中，xi为原始输入值；xmax和 xmin分别为原始输入值的最大值和最小值；xi′为归一化后的值。

2）LS－SVM参数初始化。设置C和σ初始值，令C＝100，σ＝1．5，并设置适应度值计算公式，具体如下：

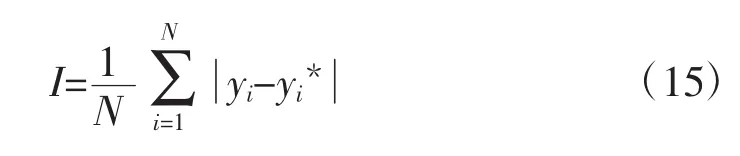
式（15）中，N 为样本容量，为 i时刻电价实际值，yi＊为i时刻电价预测值。

3）PSO算法参数设置。设置种群规模为30，加速因子均为2．05，最大迭代次数为300，惯性权重设为递减方式，递减范围为 0．9→0．4。

4）将 C 和 σ 作为优化目标，并将 C＝100、σ2＝2．5当前个体最优解，计算初始适应度值，并记为当前最优适应度值。

5）开始迭代计算，根据PSO算法速度和位置更新公式更新粒子速度和位置，并计算更新后粒子群新适应度值。

6）将新适应度值与当前最优适应度值进行比较，如果新适应度值优于当前最优适应度值，则将新适应度值更新为当前最优适应度值，否则不变。

7）重复步骤（6），并根据迭代终止条件（达到目标精度或最大迭代次数）判断是否终止迭代，若是，则转到下一步，否则，返回步骤（5）继续迭代。

8）结束计算，输出C和σ的优化结果，并将C和σ的最优值赋给LS－SVM，对电价进行预测。

3．2 模型的评价

本文采用平均相对误差和均方根误差对电价预测模型的预测效果进行评价，平均相对误差和均方根误差的计算公式分别如下：

式（16）中，N为样本容量，yi为i时刻电价实际值，yi＊为i时刻电价预测值。

4 算例分析

本文采用澳大利亚昆士兰州2017年6月的电价数据进行算例分析，电价采集的时间间隔为1h／次，30天的电价数据共720组，为了便于描述，按照时间顺序将其编号为1～720，具体如图2所示。为了建模需要，将前648组数据作为训练集，用于电价预测模型的训练，后72组数据作为测试集，用于检验模型的预测精度。

图2 6月份负荷数据

电价变化受历史电价的影响较大，为了确定电价预测模型的支持向量，首先根据经验假设t时刻电价受前3个时刻历史电价影响较大，即支持向量m＝3，采用 t－3、t－2 和 t－1 时刻电价预测 t时刻电价，利用训练集数据进行训练，采用PSO算法对LSSVM的C和σ进行寻优，求得的最优解为C＝48．36、σ＝2．25，以C和σ的最优解为LSSVM 参数，并以不同的支持向量（m＝1，2，…，8）建立基于 PSO 优化LS－SVM的电力现货市场价格预测模型，利用训练集数据进行训练，不同支持向量的训练误差如表1所示。

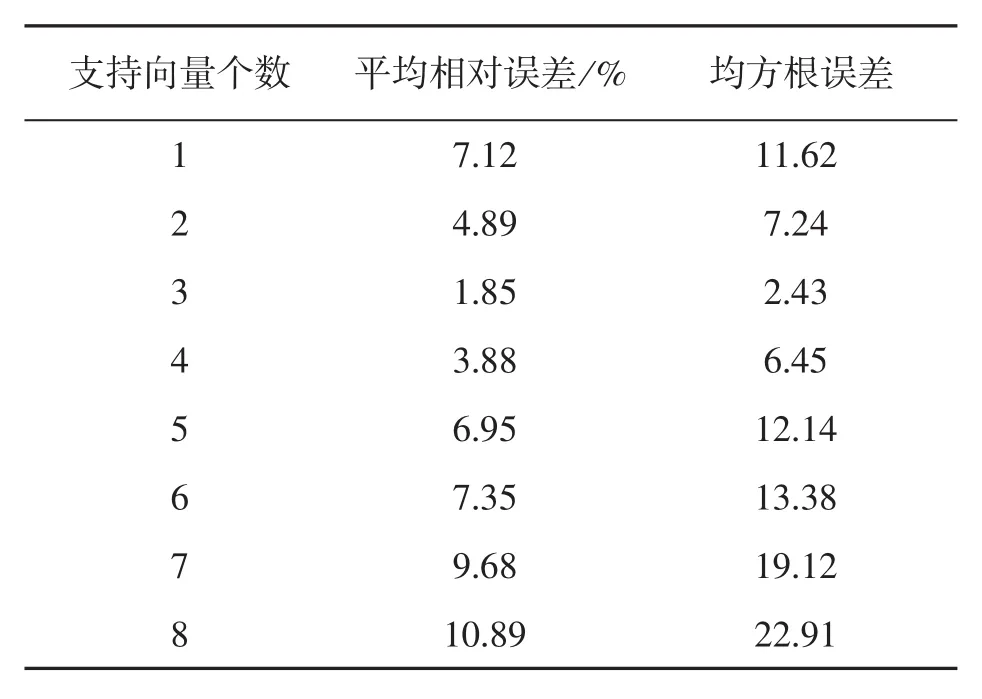
表1 不同支持向量的训练误差

由表1可知，当支持向量的个数为3时，训练集平均相对误差和均方根误差均为最小，分别为1．85%和2．43，说明了t时刻电价受前3个时刻历史电价影响较大，验证本文支持向量选择3的正确性。图2给出了支持向量m＝3时模型的训练误差，由图3可知，训练集误差区间为（－0．04，0．05），误差波动较小，模型的训练效果较好。

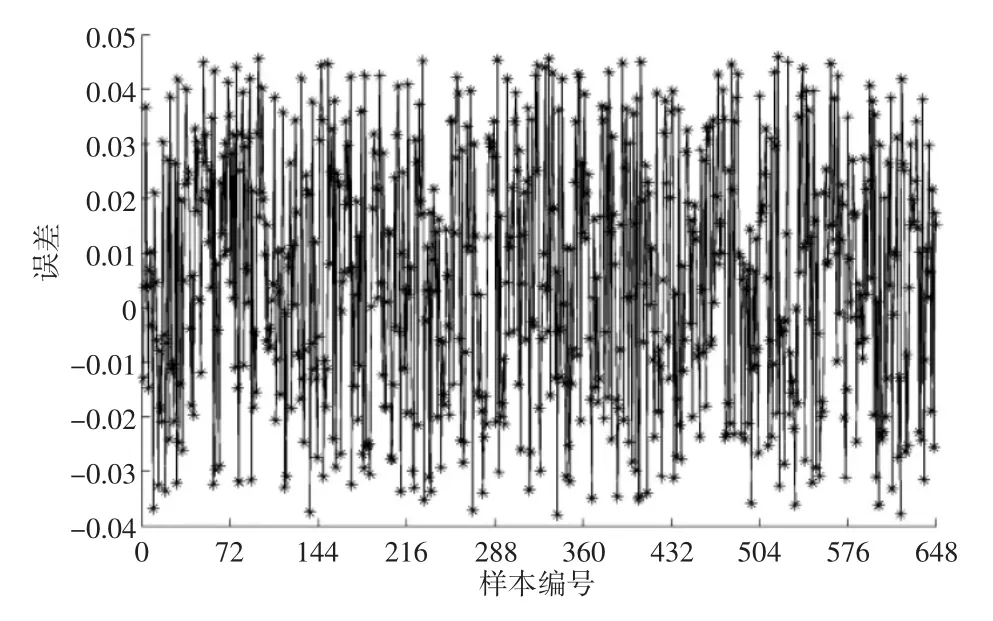
图3 模型训练误差

基于PSO优化LS－SVM的电力市场价格预测模型训练完成后，利用模型对测试集进行预测，预测结果如图4所示，由图4可知，电价预测值与实际值较接近，电价预测值变化趋势与实际变化趋势基本一致，可见预测效果较好。

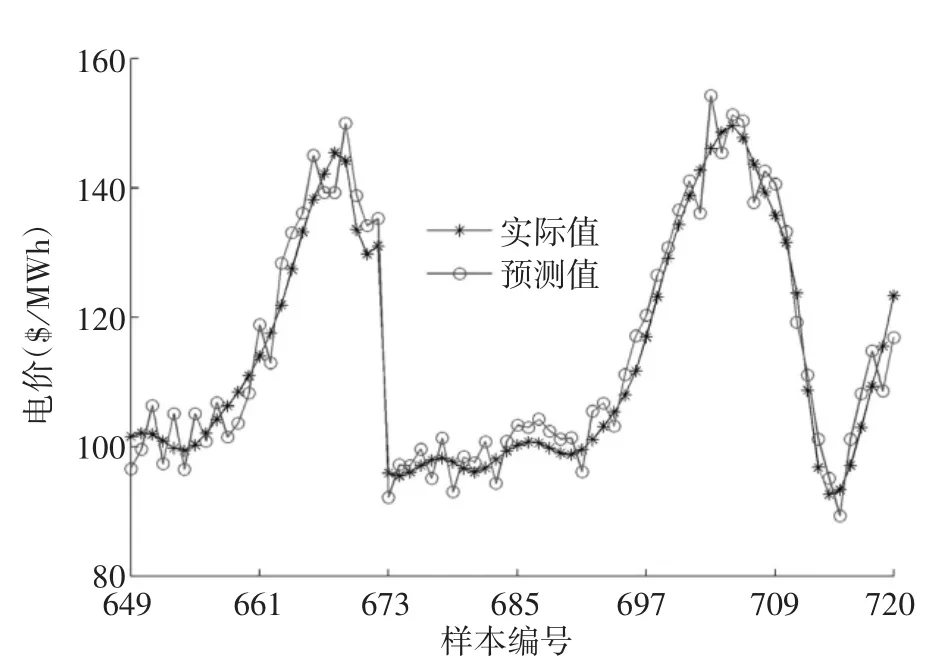
图4 测试集预测结果

根据平均相对误差和均方根误差计算公式，表2给出了PSO优化LS－SVM模型对测试集预测的平均相对误差和均方根误差，为了对比说明本文电价预测模型的预测效果，分别建立遗传算法（Genetic Algorithm，GA）优化SVM的电价预测模型和PSO优化BP神经网络的电价预测模型，对测试集数据进行预测，预测结果的平均相对误差和均方根误差也展示在表2中，从表2中三种电价预测模型的预测误差可以看出，PSO优化LSSVM模型的平均相对误差和均方根误差分别为4．51%和6．96，均小于GA优化SVM模型和PSO优化BP模型，验证了本文提出的电价预测模型的正确性和优越性。

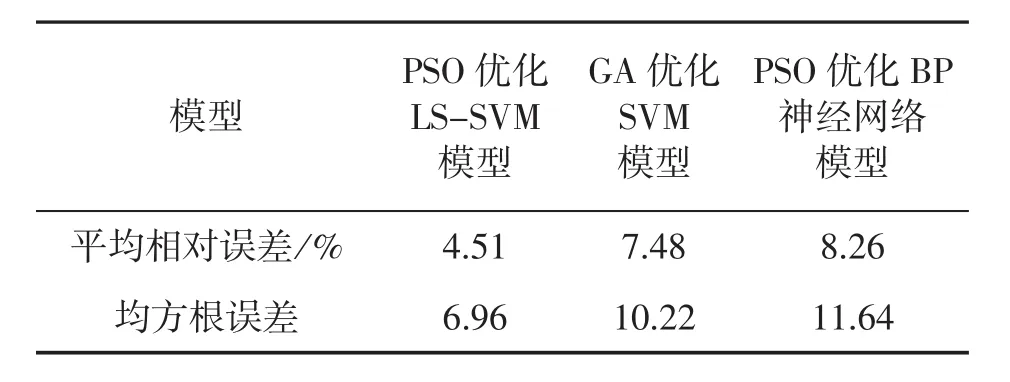
表2 不同支持向量的训练误差

5 结论

本文采用粒子群优化算法对最小二乘支持向量机的惩罚因子和径向基核函数宽度进行优化，解决了LS－SVM参数选择盲目性问题，建立了基于PSO优化LS－SVM的电力现货市场价格预测模型。采用实际电价数据对模型的正确性和实用性进行验证，并与其他常用的电价预测模型进行对比，验证了本文提出的电价预测模型的正确性和优越性。