高超声速气流中头锥逆喷防热流热耦合分析 *

尹 亮，刘洪鹏，刘伟强

(1. 湖南文理学院 机械工程学院， 湖南 常德 415000； 2. 国防科技大学 空天科学学院， 湖南 长沙 410073)

对于高超声速飞行器，特别是其头锥和前缘等尖锐部件，由于高速空气滞止和摩擦作用，其表面面临严重的气动加热环境，这给飞行器的安全设计带来巨大挑战[1-4]。对于长时间飞行，传统的烧蚀结构不再适于承担防热任务：一方面，烧蚀由于质量的减损，飞行器表面结构的改变带来了气动环境的改变，表面粗糙度的增加还增大了摩擦阻力；另一方面，烧蚀结构不满足可重复性使用，增加了飞行器的使用成本。而作为一种主动冷却技术[1,5-6]，逆向喷流技术在减阻和防热方面具有显著效果[7-8]。

逆向喷流技术的减阻和防热前景，最初由Lopatoff[9]和 Warren[10]提出，他们采用先进的试验和数值计算工具，进行了相关机理性研究。Hayashi等[11-12]采用试验和数值方法对单孔逆向喷流的减阻和防热特性进行了研究，其中自由来流马赫数为3.98，数值计算采用k-ω湍流模型，其研究结果表明逆向喷流总压和自由来流总压的比值对逆向喷流的流动模式起着关键作用。Li等[13]研究了乘波体前缘多孔逆喷结构的减阻和防热特性，采用k-ω湍流模型进行数值计算，结果表明多孔喷流相对于缝隙喷流的防热效果更加优越；当喷流孔径一定时，存在最佳喷孔间隔，使得减阻和防热效果达到最优。Huang等[14-15]还研究了逆向喷流和其他防热措施的组合热防护性能，包括激波针和凹腔等结构，其研究结果表明组合结果的防热效果更佳，并且由逆喷所带来的流场振荡和其他结构之间的非稳态模型之间存在相互耦合效应。

目前，大部分的数值计算研究是基于固体结构表面的均匀冷壁温假设而开展的，忽略了流体和固体结构之间的热交互作用，这主要会带来气动热环境的过考核问题。此外，这种与物理事实不相符合的假设，不利于对防热机理的进一步认识。事实上，固体结构气动加热的降低是和壁面温度相关的。

为了对逆向喷流中的流动和传热特性进行更好的理解，本文采用共轭传热方法，对6马赫飞行条件下的头锥逆喷结构中的流热交互过程进行数值分析。首先介绍所采用的数值计算模型和流热耦合方法，并分别与相关试验结果对比，验证其准确性。然后对不同喷流压力情况下的减阻和防热效果进行数值计算，并进一步讨论不同攻角对防热效果的影响。为了研究固体结构的热响应情况，分别采用IN718和C-103高温难熔合金材料，对其传热特性进行对比分析。

1 物理模型和数值方法

1.1 物理模型

物理模型如图1所示，由于对称性，图中仅给出了纵向截面的1/2结构。其中，头部半径为6 mm，半楔角φ为10°，头锥长度L为100 mm，逆喷喷口直径d为1.2 mm。飞行高度假定为25 km，飞行马赫数为6。逆喷相比于自由来流的总压，即总压比(Pressure Ratio, PR)为0.092。逆喷气流温度为300 K，逆喷马赫数为1。头锥材料采用高温难熔合金IN718和C-103，头锥结构厚度设定为3 mm。

图1 物理模型简图Fig.1 Diagram of physical model

1.2 数值方法

对于气动环境的预测，采用三维Navier-Stokes (N-S)方程作为控制方程。为了提高计算准确性，对流项采用AUSM-DV格式和MUSCL方法近似处理，黏性项采用中心差分格式。由于逆喷和自由来流之间，以及边界层附近强烈的流动剪切作用，数值计算采用k-ω(SST)模型。固体域采用热传导控制方程，并在固体表面增加向周围环境的热辐射项，金属固体表面辐射系数假定为0.8。

流热耦合采用如下方法：

步骤1：初始时刻t0，为固体结构指定均温温度300 K，并将流固交界面的温度传输至流体域，并作为流动计算的边界条件。

步骤2：采用传输至流体域的温度边界条件，对流场进行稳态计算，得到流固交界面上的气动热环境。

步骤3：将流固交界面上的气动热分布传输至固体域，并基于该气动热边界条件计算t0至t0+Δtc时刻固体域的瞬态传热。

步骤4：将计算所得的t0+Δtc时刻流固交界面温度传输至流体域，并作为新的边界条件进行流场计算。

步骤5：重复以上步骤2～4，直至完成所有时间步计算。

2 数值方法验证

2.1 湍流模型验证

流体域的计算采用FLUENT商业软件，结构传热采用Abaqus软件，通过编程实现数据传输。为了验证湍流模型的准确性，将计算结果与文献[11]中的实验结果进行了对比。相关实验设置参数如表1所示。图2给出了数值计算和实验测量的流场密度分布对比，可以看出流场计算中，马赫盘、回流区和再压缩激波均得到了较好的捕捉，并且和实验结果较为一致。

表1 实验参数

图2 密度分布的计算和实验结果对比Fig.2 Comparison of density distribution between numerical and experimental results

图3 St分布对比Fig.3 Comparison of St distribution

图3为固体表面的斯坦顿数(St)分布，其中θ为球头外表面和自由来流方向间的夹角。斯坦顿数是一个无量纲数，用于测量传递到流体中的热量与流体的热容量之比。由图3可以看出，数值计算和实验结果的分布趋势较为一致。除了左边第一个测点，大部分的结果偏差在15%以内。该偏差可能是由数值计算模型的假设以及实验测量误差所引起的。总的来说，数值计算和实验测量的流场和传热分布结果吻合较好，证明了逆向喷流所采用的数值模型的适用性。

2.2 流热耦合方法验证

为了验证流热耦合方法的准确性，将计算结果与实验测量结果进行对比。其中，实验结果采用1987年于NASA兰利中心开展的高速气流中的圆管气动加热实验，来流马赫数为6.47，管材为不锈钢，其他实验参数参照文献[16]。

为了节省计算资源，仅对气动加热严重的圆管前半部分进行数值计算。为了保证气动热计算的准确性，流体域近壁面第一层网格厚度取1×10-5m，固体域第一层网格厚度取1×10-4m，流固交界面附近的固体域和流体域均进行了网格加密，如图4所示。

图4 流体域和固体域网格分布Fig.4 Grid distribution of fluid domain and solid domain

图5为圆柱表面热流分布随时间的变化，实验数据为冷壁温时的测量结果[16]。其中q为任意时刻圆柱驻点热流，q0为0 s时圆柱驻点热流。由图5可以看出，0 s时数值计算和实验结果较为一致。数值结果表明，在加热时间1 s内，驻点位置的气动热流值迅速下降，而后部区域的热流降低幅度较小。这表明，采用流热耦合方法对准确计算气动热分布是非常重要的，而采用均匀的冷壁温边界条件假设将使气动热计算过考核。

图5 热流分布对比Fig.5 Comparison of heat flux distribution

图6 表面温度分布对比Fig.6 Comparison of surface temperature distribution

图6为不同时间圆管表面的温度分布，其中实验值为约5 s时的数据。由图6可以看出，大部分的实验数据位于计算所得的4 s和5 s曲线之间，其中5 s时的驻点温度比实验值高约3%，证明了数值计算和实验结果吻合良好。从图6还可以看出，随着气动加热时长增加，驻点温度上升速度远远高于圆管尾部温度上升速度，即驻点和尾部温差随之增大，这意味圆管要承受的热应力也将随之增加。

此外，驻点温度随时间的变化如图7所示。在气动加热的前1 s内驻点温度快速上升，1 s后温度上升速度较为趋缓。当驻点固体壁面温度升高时，空气滞止温度和固体壁面温度间的温差随之减小，对固体域的气动加热热流也随之减小，这可与图5中的热流分布加以相互印证。 5 s时固体结构中的温度云图如图8所示。驻点区域固体壁面由于气动加热最为严重，其温度最高。温度云图的温度梯度分布清晰表明固体内由圆管外壁面向内壁面的导热以及沿着圆管周向上由驻点向尾部的导热。

图7 驻点温度随时间的变化Fig.7 Stagnation temperature changes with time

图8 固体温度分布(t=5 s)Fig.8 Solid domain temperature distribution(t=5 s)

3 计算结果

3.1 流动与传热性能

采用IN718作为结构材料，对逆喷总压比PR=0.092的工况进行数值计算，温度、压力和流体速度计算结果如图9所示。由图9可以看出，气体自喷口逆向喷出后迅速膨胀，形成马赫盘，该马赫盘主要是激波后压力和逆喷压力的平衡结果。逆喷和自由来流相互作用结果对减低气动加热起到了直接作用：一是逆向喷流将激波推离固体壁面，并且将高温气体封装于远离固体壁面处；二是环喷口附近形成了低温低压回流区，这对头部区域冷却具有积极作用。此外还可以看到，在气体再附层的下游形成了再压缩激波，此处高温高压的气流流向近壁面区域，会造成此处气动热的升高。

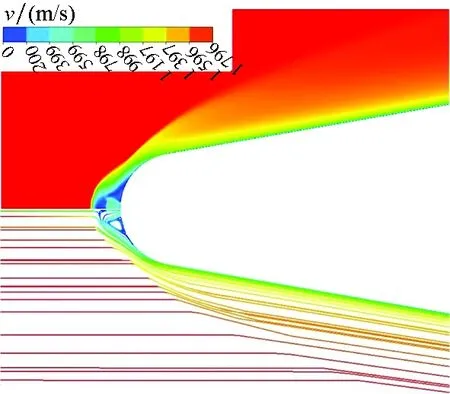
(a) 速度场分布(a) Velocity distributions

图9 速度场、温度场及压力场分布(PR=0.092)Fig.9 Velocity,temperature and pressure distributions (PR=0.092)

图10 不同时刻热流分布Fig.10 Heat flux distribution at different times

图10为热流分布随时间变化的计算结果。可以看出，在2 s时，固体壁面的最大热流由1.29 MW/m2降低至0.78 MW/m2，降低幅度约为40%；60 s时，最大热流值降低至0.29 MW/m2，降低幅度约为78%。此外，60 s时尾端的热流降低幅度约为68%。显然，采用均匀的冷壁温边界条件假设，将带来气动热环境的严重高估，这对结构设计提出了更为苛刻的要求。固体表面的温度变化如图11所示。可以看出，固体壁面的最高温度位于气流再压缩区域，同时可以看到固体壁面受气动加热后的升温过程。60 s时固体表面的温度分布云图如图12所示。可以看出，60 s时固体表面最高温度位于气流的再压缩区。

图11 不同时刻结构表面温度分布Fig.11 Surface temperature distribution at different times

图12 60 s时固体表面温度分布云图Fig.12 Solid surface temperature distribution at t=60 s

3.2 总压比的影响

图13比较了总压比PR=0.092 (图中上半部分)和PR=0.184(图中下半部分)的流场计算结果。可以看出，当总压比增大到0.184时，弓形激波和高温气体均被进一步推离头锥的头部区域。从图中还可以看出，总压比增大时，逆向喷流的出流膨胀角有所增大，环出流的低温回流区域也有所增大，这将有利于头部区域的进一步冷却。此外，再压缩区域也受到总压比增大的影响，总压比增大时，再压缩激波同样被进一步推离固体壁面，这将使得肩部附近的最大热流值有所降低。

图13 不同总压比时温度场和速度场分布Fig.13 Temperature and velocity distributions at different total pressure ratio

图14比较了没有逆喷、逆喷总压比PR=0.092和PR=0.184时壁面热流分布的对比。可以看出，在数值模拟时间段的起始和最终时刻，采用逆喷结构后壁面的最高热流均有了大幅度的下降；当总压比PR由0.092增大到0.184时，壁面最高热流有了更进一步的降低，这主要是由于流场结构改变的结果。

图14 不同总压比时热流分布Fig.14 Heat flux distribution at different total pressure ratio

此外，图14中可以看到，逆喷总压比变化时，环出流的气流回流区和再压缩区域是受影响最显著的区域。由于逆向喷流冷空气的注入，固体表面得到冷却，其温度也随之得到了大幅度的降低，并且固体结构的温度分布整体上更加均匀：其中，PR=0.092时固体表面温差降低了55.5%，PR=0.184时固体表面温差降低了83.1%，如图15所示。

图15 不同总压比时固体壁面温度分布Fig.15 Solid surface temperature distribution at different total pressure ratio

3.3 攻角的影响

本小节通过数值计算比较不同攻角对气动加热环境的影响，其中设定PR=0.138，攻角分别取0°、2°和5°。其中5°攻角时，对称面上的流场密度和温度分布云图如图16所示。可以看出，迎风面上的再压缩激波明显薄于背风面，这意味着在肩部区域，迎风面处的高温气流更加流向固体表面，这也必然带来此处气动加热环境的恶化。

图16 5°攻角时流场云图Fig.16 Flow field contour when the attack angle is 5°

图17为0 s和60 s时迎风面和背风面中心线上的热流分布。由图17(a)可以看出，随着攻角的增加，迎风面肩部区域的热流值增大幅度较大，当攻角增大到5°时，最大热流值相比于无攻角时增大超过60%，而背风面的热流值相应得到大幅度降低。这主要是攻角的增大使得迎风面和背风面的激波厚度均得以改变所致，如图16所示。相应地，在头锥尾部区域的迎风面和背风面上，气动热流也分别有不同程度的增大和减小。60 s时固体表面的热流分布如图17(b)所示，在球头的肩部区域，迎风面中心线上的热流随攻角的增大而增大，背风面中心线上的热流随攻角的增大而减小。当攻角为2°时，在头锥的尾部区域，60 s时迎风面中心线上的热流分布相较于0°时变化不大，这主要是由于攻角增大幅度较小时，尾部区域激波厚度变化相对不显著，并且受流体和固体之间的耦合传热以及固体内部的导热所影响。此外还可以看出，60 s时喷口附近的热流为负值，并且在背风面处负值区域相对更大，这是由于攻角导致逆向出流更容易流向流场压力较低的背风面，从而使背风面得到冷气流更好的冷却效果。

(a) 0 s时的热流分布(a) Heat flux distribution at 0 s

(b) 60 s时的热流分布(b) Heat flux distribution at 60 s图17 不同攻角下的热流分布Fig.17 Heat flux distribution at different attack angle

图18为60 s时固体表面的温度分布，可以看出攻角的增大使得固体表面的温差得以大幅度增大，这对材料的耐高温性能和力学性能提出了更严苛的要求。

图18 不同攻角下温度分布Fig.18 Temperature distribution at different attack angle

3.4 材料的影响

图19 不同材料热流分布Fig.19 Heat flux distribution of different materials

如前所述，逆向喷流中的传热实际上是流体和固体结构间的动态交互过程，所以本小节对材料的影响进行对比研究，其中头锥飞行攻角为0°，PR=0.184。图19为10 s和60 s时刻固体壁面的热流分布，固体材料分别为IN7118和C-103。可以看出，不同材料下头部区域的热流分布比较一致，尾部区域差异相对明显，这是因为：头部区域受逆向出流的影响较为显著，回流区中的对流冷却对头部区域的防热占主导因素；而尾部区域则以固体结构内部的热传导为主，不同材料的热物性导致固体内部的传热速度不同，从而进一步影响了流体和固体表面的耦合传热情况。图20为固体结构内表面和外表面的温度分布，可以看出选用C-103为固体结构材料时结构温度分布更为均匀，这主要是因为C-103有着更大的导热系数，从而使加热过程中固体结构内部的温差更小。图21为固体结构最高温度随时间的变化，可以看出不同材料下固体最高温度的变化较为一致，这与图19中不同时刻下不同材料表面的最高热流较为一致是相吻合的。

图20 结构内外表面温度分布(t=60 s)Fig.20 Inner surface and outer face temperature distribution (t=60 s)

图21 不同材料结构表面最高温度随时间的变化Fig.21 Maximum surface temperature for different materials with time

4 结论

采用流热耦合方法，对6马赫下的头锥逆喷结构的流动与传热特性进行了数值研究。基于对湍流模型和流热耦合方法的验证，针对不同逆喷总压比、攻角和材料对头锥防热效果的影响进行了对比研究。主要结论如下：

1)对于逆向喷流结构，为了获得准确的气动加热环境，采用流热耦合进行相关计算非常必要。与流热耦合数值计算方法相比，基于均匀冷壁温边界条件假设的热流计算值被严重高估。

2)冷气流回流区和再压缩激波对逆喷结构的防热起着关键作用。随着总压比的增大，冷气流回流区域增大，再压缩激波被进一步推离固体表面，致使固体结构得到更大幅度的冷却。采用逆向喷流结构以后，固体结构温度下降显著，结构整体温度分布更加均匀。

3)当头锥攻角大于0°时，迎风面热流得以增大，背风面热流减小；头部环出流的冷气流回流区和再压缩激波的厚度受影响明显。攻角增大时，固体结构内的温差增大幅度显著，这给固体材料的热和力学性能提出了更严苛要求。

4)对于IN718和C-103两种不同材料，其在头部气动加热环境的差异可以忽略。整体上，采用C-103作为结构材料时，结构内的温度分布更为均匀，这主要得益于C-103较大的导热系数。