太赫兹粗糙金属目标镜面雷达散射截面预估方法 *

逄 爽，曾 旸,2，杨 琪，邓 彬，王宏强

(1. 国防科技大学 电子科学学院, 湖南 长沙 410073; 2. 国防科技大学 气象海洋学院, 湖南 长沙 410073)

雷达散射截面(Radar Cross Section, RCS)是衡量目标对入射电磁波散射能力的一个重要物理量，是雷达探测、目标识别、隐身与反隐身研究的重要基础。在现代军事对抗技术领域中，军用目标的RCS是重要战技术指标之一。缩比测量是获取目标RCS的主要方式之一[1-4]。为了实现对大尺寸目标(如舰船)的缩比测量，根据缩比规律，缩比频段将上升到太赫兹(Terahertz, THz)频段，这对太赫兹频段RCS的缩比测量提出新的挑战。

太赫兹波(0.1～10 THz)是微波与红外波之间的一个过渡频段，其低频段覆盖了毫米波波段，高频段覆盖了远红外波段，处于由宏观电子学向微观光子学过渡的频段。与微波相比，太赫兹波波长更短，因而在缩比测量方面可以实现更高的缩比因子，从而更加适合于对电大尺寸目标的缩比测量与理论研究。与此同时，由于太赫兹波频率更高，波长更短，对目标表面粗糙度、细微结构等也更加敏感，这使得对太赫兹频段目标RCS的研究比微波频段更加复杂。关于太赫兹频段粗糙金属目标的散射特性的研究表明[5-6]，微波频段光滑的金属目标在太赫兹频段变为粗糙度不可忽略的粗糙金属目标，这意味着在太赫兹频段研究金属目标的散射特性以及RCS缩比关系，需要对粗糙度等影响因素加以考虑。

典型粗糙面散射理论计算方法[7]包括基尔霍夫近似方法(Kirchhoff Approximation，KA)、微扰法(Small Perturbation Approximation，SPA)、组合大小尺度的双尺度近似法(Two scale Approach，TA)和基于积分方程的粗糙面近似法(Integral Equation Method，IEM)等。近几年，国内外针对太赫兹频段粗糙目标散射特性展开了深入的研究。美国亚毫米波技术实验室(Submillimeter-wave Technology Laboratory，STL)通过对粗糙模型散射系数进行测量，并与KA算法的计算结果进行比对，证明了KA方法在太赫兹频段的适用性[8]。陈珲等在微波建模方法基础之上，对太赫兹频段表面随机粗糙结构和复杂细微结构的散射特点进行建模方法的拓展，研究并提出基于“半确定性”描述的射线追踪高频算法，实现了超电大复杂目标表面相干和非相干散射特性的一体化快速建模，为太赫兹超电大复杂目标的散射特性建模分析提供高效的方法[5]。陈刚等采用物理光学法(Physical Optics，PO)结合截断劈增量长度绕射系数法(Truncated-Wedge Incremental Length Diffraction Coefficients，TWILDC)和微扰法计算了太赫兹低频段随机粗糙金属板的电磁散射分布及其雷达散射截面[9]，给出了一种有效的理论计算方法。高敬坤等针对太赫兹全尺寸凸体粗糙目标，在激光RCS计算方法的基础之上，提出一种基于面片分级与粗糙面全波法的目标散射建模与雷达回波仿真方法[10-11]，使得在有限的存储空间和合理时间范围内，计算THz超电大目标的散射特性成为可能。

尽管目前有多种关于粗糙目标RCS的计算方法，但要通过仿真计算获得某一粗糙目标的RCS，需要经过粗糙模型的构建、面元剖分与仿真计算等复杂过程。在太赫兹频段，由于太赫兹波波长短，目标模型多为电大尺寸，上述过程的数据量与计算量剧增，耗时较长。此外，对于太赫兹频段的粗糙目标RCS缩比测量，需要一种便捷的粗糙目标RCS预估方法，便于与测量数据进行比对。因此，考虑通过测量值对相应范围内的粗糙目标镜面RCS进行预估。为了实现对太赫兹频段粗糙目标RCS的预估，本文结合金属目标镜面散射RCS随表面粗糙度的变化规律，在特定的参数区间内，提出基于基尔霍夫近似的粗糙目标镜面散射RCS预估方法，通过仿真实验证明了预估方法的有效性，有望为太赫兹粗糙目标RCS缩比测量提供支持。

1 理论分析

典型粗糙面散射特征的研究方法(如KA、SPA、TA、IEM)主要从解析计算的角度分析随机粗糙面的散射特点，给出定量的结果分析，但计算过程复杂，且适用的范围有限。基尔霍夫近似理论采用的是切平面近似，界面上任意一点的场强由该点处的切平面反射波决定[7]。基尔霍夫近似方法适用于高频条件下平缓型的粗糙面散射问题，要求粗糙面平均曲率半径远大于入射波波长，相关长度和粗糙面随机起伏的方差也均大于波长。

文献[8]在基尔霍夫近似条件下，主要考虑粗糙表面起伏均方根高度hrms的影响，建立了粗糙表面与光滑表面镜面反射系数之间的关系，如式(1)所示。

Rrough=Rsmoothe-(4πhrmskcosθ)2

(1)

其中，Rrough是粗糙表面的镜面反射系数，Rsmooth是光滑表面的镜面反射系数，θ是入射角度，k是波数。式(1)的适用条件为：粗糙面随机粗糙并服从正态分布；粗糙面的相关长度远大于波长；没有多重散射。

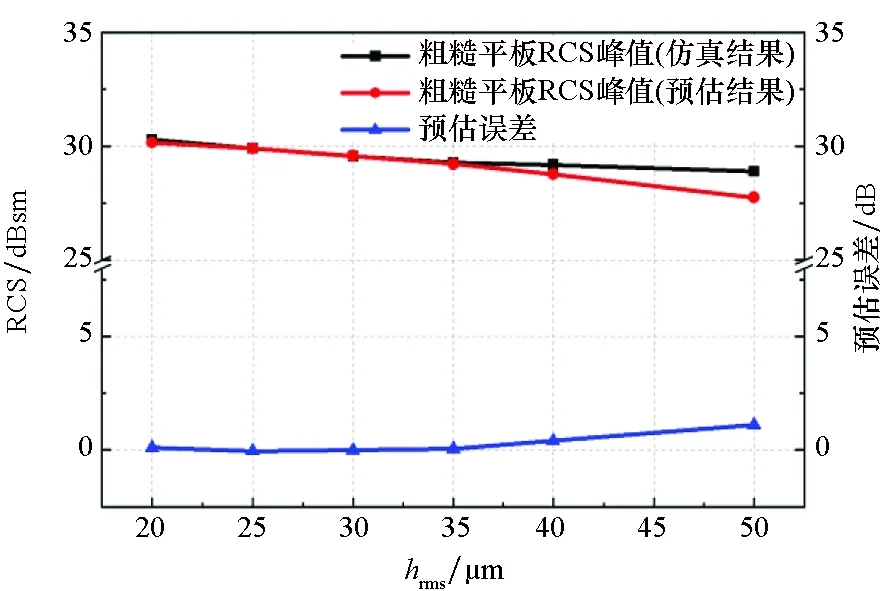
本文在太赫兹低频段(0.1～0.5 THz)研究粗糙起伏对电大尺寸目标RCS的影响，粗糙表面均方根高度小于波长(λ/150

Rrough=Rsmooth·e-{[4πhrms(1+x)kcosθ]2+y(λ/l)2}

(2)

其中，x和y为引入的待定系数。通过对式(2)的指数幂展开，发现指数幂中包含待定系数x的二次项，相比于一次项，其贡献可以忽略。此外，本文关注粗糙起伏对镜面反射的影响，入射角θ为0°，式(2)进一步整理如下：

Rrough=Rsmooth·e-[(8π2hrms/λ)2(1+2x)+y(λ/l)2]

(3)

对于表面光滑的理想电导体(Perfect Electric Conductor，PEC)目标，其镜面反射系数Rsmooth为1，由式(3)可得表面粗糙的PEC目标的镜面反射系数预估公式为：

Rrough，PEC=e-[(8π2hrms/λ)2(1+2x)+y(λ/l)2]

(4)

进一步，根据相干散射理论[9]，表面粗糙的PEC目标镜面RCS可以视为粗糙镜面反射系数对光滑目标镜面RCS的调制，因此，选取粗糙镜面反射系数作为调制因子，如式(5)建立粗糙PEC目标和光滑PEC目标的镜面RCS的关系：

(5)

其中，σr表示粗糙金属目标镜面散射方向的RCS，σs表示与粗糙金属目标具有相同形状、相同尺寸的光滑金属目标的RCS。式(5)可以具体表示如下:

σr=σs·e[-2(8π2hrms/λ)2(1+2x1)+y1(λ/l)2]

(6)

其中，x1、y1为待定参数，具体取值与粗糙目标的形状、电尺寸有关。若两个随机粗糙模型满足经典电磁相似律，即具有相同的形状以及相同的电尺寸，当粗糙面的均方根高度在特定区间内时，可以利用这两个不同频段的RCS值来求解待定系数，所得的预估公式在两个频段相应的均方根高度区间内均可使用。

2 仿真实验及结果分析

为了检验所提预估公式对镜面散射RCS的预估效果，选取具有镜面反射的金属平板和金属圆柱两种目标模型进行相应的仿真实验。首先，根据文献[12]介绍的粗糙模型生成方法，生成了服从高斯分布的粗糙平板和粗糙圆柱模型；其次，将粗糙模型和同尺寸光滑模型分别导入电磁仿真计算软件，采用弹跳射线追踪法进行RCS仿真计算；然后，提取镜面反射的RCS值，代入所提预估公式求解待定参数；最后，对特定参数区间内的粗糙平板、粗糙圆柱的镜面RCS进行预估，并将预估结果与仿真计算结果进行比对，以此验证所提预估方法的有效性。

为了检验仿真计算结果的可靠性，首先对具有解析解的标准体平板模型(220 GHz, 5 cm)进行仿真计算，结果如图1所示。仿真计算结果与理论计算结果一致，说明仿真计算结果可靠。

图1 光滑平板RCS理论计算与仿真计算结果比对Fig.1 Comparison between theoretical RCS and simulated RCS of the smooth plate

为了进一步验证预估公式的有效性，生成了四组粗糙金属模型，分别检验预估公式在不同的均方根高度区间、不同电尺寸、不同形状条件下的预估效果，具体实验设计如下：

1)检验预估公式在不同的均方根高度区间内的预估效果。按照相应的区间生成两组粗糙平板模型并进行RCS仿真计算。第一组实验中，粗糙平板模型的均方根高度主要分布区间为λ/150

2)检验预估公式对不同电尺寸粗糙平板镜面散射RCS的预估效果。本组(第三组)实验中粗糙平板模型的电尺寸为第一组粗糙平板电尺寸的两倍，均方根高度的主要分布区间为λ/150

3)检验预估公式对粗糙金属圆柱镜面散射RCS的预估效果。本组(第四组)实验采用的粗糙金属圆柱模型与第一组实验中的粗糙平板电尺寸相同，粗糙圆柱表面均方根高度主要分布区间为λ/150

每组仿真实验均在110 GHz、220 GHz、440 GHz三个频段进行。具体每组仿真实验模型的尺寸、均方根高度和相关长度参见相关列表。

2.1 预估公式在λ/150

第一组实验中，粗糙平板模型的均方根高度取值主要分布区间为λ/150

表1 第一组仿真实验参数

仿真实验中选取110 GHz (hrms=30 μm,l=4 000 μm) 和220 GHz (hrms=20 μm,l=2 000 μm) 两个粗糙平板的镜面散射RCS值代入预估公式(6)，得到待定系数x1=-0.449 2,y1=-1.890 1，再将其代入预估公式，进一步对上述三个频段的其他粗糙度模型的镜面散射RCS进行预估，不同频段预估值与仿真计算值如图2所示。

(a) 110 GHz

(b) 220 GHz

(c) 440 GHz图2 第一组实验粗糙平板RCS预估值与计算值对比Fig.2 Comparison between estimated RCS and simulated RCS of rough plates at the first set of simulations

如图2(a)所示，在110 GHz频段、边长为10 cm的粗糙平板，预估效果较好的均方根高度区间为20～40 μm，对应均方根高度与波长的关系为λ/150

图2(b)给出的是220 GHz频段、边长为5 cm的粗糙平板在特定区间内的预估值和仿真值对比。由结果可以看出，在10～20 μm内，平板镜面RCS的预估误差较小。根据图2(c)所示，在440 GHz频段、边长为2.5 cm的平板，镜面RCS预估效果较好的区间为5～10 μm。上述结果均表明，所提预估公式在λ/150

2.2 预估公式在0.1λ

在第二组仿真实验中，粗糙平板的均方根高度分布区间为0.1λ

表2 第二组仿真实验参数

对该区间预估公式待定系数的求解，选取110 GHz (hrms=0.11λ1,l=1.5λ1)的粗糙平板和220 GHz (hrms=0.14λ2,l=1.5λ2)的粗糙平板相关参数作为已知条件，求出待定参数为x1=-0.497 3，y1=-2.489 3。不同频段的预估结果和仿真结果如图3所示。

(a) 110 GHz

(b) 220 GHz

(c) 440 GHz图3 第二组实验粗糙平板RCS预估值与计算值对比Fig.3 Comparison between estimated RCS and simulated RCS of rough plates for the second set of simulations

通过不同频段的预估误差对比来看，频段为220 GHz和440 GHz时，在该区间，粗糙平板峰值RCS的整体预估效果较好；在110 GHz频段，均方根高度取值在0.1λ～0.13λ时，粗糙平板峰值RCS预估误差较小。第二组仿真实验的均方根高度取值比第一组仿真实验的要大，对RCS的影响出现了不同于小粗糙度时的变化规律，情况更复杂。

2.3 预估公式对不同电尺寸粗糙平板的预估效果检验

第三组仿真实验中，粗糙平板的电尺寸是第一组实验中粗糙平板的两倍，均方根高度主要分布区间为λ/150

表3 第三组仿真实验参数

选取110 GHz(hrms=30 μm,l=4 000 μm) 和220 GHz (hrms=20 μm,l=2 000 μm) 两个粗糙平板的镜面散射RCS值代入预估公式(6)，得到待定系数x1=-0.421 5,y1=-1.719 4，再将其代入预估公式，对上述三个频段的其他粗糙度模型的镜面散射RCS进行预估，不同频段预估值与仿真计算值如图4所示。

(a) 110 GHz

(b) 220 GHz

(c) 440 GHz图4 第三组实验粗糙平板RCS预估值与计算值对比Fig.4 Comparison between estimated RCS and simulated RCS of rough plates for the third set of simulations

由图4可以看出，预估公式对第三组粗糙平板的预估效果与第一组的预估效果大致相同，说明对于区间λ/150

2.4 预估公式对粗糙圆柱的预估效果检验

第四组仿真实验构造了特定粗糙度的金属圆柱模型，对粗糙柱面的RCS进行预估，具体模型参数见表4。

表4 第四组仿真实验参数

选取110 GHz (hrms=30 μm,l=4 000 μm) 和220 GHz (hrms=20 μm,l=2 000 μm) 两个粗糙圆柱侧面的镜面散射RCS值代入预估公式，得到待定系数x1=-0.442 9,y1=-1.734 7，进一步对上述三个频段的其他粗糙度模型的镜面散射RCS进行预估，不同频段预估值与仿真计算值如图5所示。

通过上述粗糙圆柱侧面镜面散射RCS的预估结果可以看出，该方法对单弯曲表面的镜面散射同样适用。由此可以说明该预估公式在特定条件下可以很好地对粗糙金属目标的镜面RCS进行预测，为特定条件下粗糙金属目标的缩比关系研究提供有效的比对数据。

(a) 110 GHz

(b) 220 GHz

(c) 440 GHz图5 第四组实验中粗糙圆柱RCS预估值与计算值对比Fig.5 Comparison between estimated RCS and simulated RCS of rough cylinders for the fourth set of simulations

3 结论

太赫兹频段电大尺寸粗糙金属目标散射特性建模与仿真计算存在计算量大、耗时长、难以满足RCS缩比测量需求的问题。本文通过分析太赫兹粗糙金属目标镜面散射RCS随粗糙度的变化规律，提出基于基尔霍夫近似的粗糙金属目标镜面散射RCS预估方法。采用所提预估方法对不同粗糙度的金属平板和金属圆柱镜面散射RCS进行预估，预估值与仿真计算值的一致性证明了该方法的有效性，表明该方法在太赫兹低频段小粗糙度范围内，可以实现对粗糙金属目标镜面散射RCS的快速预估，为太赫兹粗糙金属目标RCS的缩比测量提供有效的比对数据，对太赫兹粗糙目标散射特性的测量、分析和研究具有借鉴意义。后续工作将围绕其他形状、复杂结构的粗糙目标展开，并进一步研究非镜面角度下的RCS变化规律，为太赫兹频段的粗糙目标散射特性分析与测量提供更有力的支持。