基于快速傅里叶变换的扫描单发单收面阵近场成像技术 *
陈 旭,杨 琪,邓 彬,曾 旸,王宏强
(国防科技大学 电子科学学院, 湖南 长沙 410073)
合成孔径雷达(Synthetic Aperture Radar, SAR)目前广泛应用于遥感领域,它是一种有着全天候和高分辨率特性的成像雷达,在军事、通信和航天等诸多军用和民用领域中有其无可替代的优势[1-2]。主动式毫米波近场阵列成像系统是SAR成像技术在近场民用领域中的重要应用形式[3-4]。毫米波的优点在于它的散射特性对目标形状细节较为敏感,可以实现目标高分辨率成像,提高目标识别能力,并且它还具有一定的穿透能力和无电离辐射特性等。因此,毫米波成像技术在安防和无损检测等领域有其独特的优势[5-6]。
主动式毫米波近场阵列成像技术属于有源探测领域,通过接收并处理目标散射的电磁回波信号来对目标特性进行表征,它最早提出于19世纪70年代[7],经过半个世纪的发展,该领域在阵列构型、成像算法等方面取得了很大的研究进展[8-10]。扫描单发单收(Single-Input-Single-Output, SISO)面阵是最早也是技术最成熟的一种阵列全息体制,它是二维SAR向近场成像技术的直接推广。不同之处在于,毫米波近场成像阵列采用的SISO阵列维度与机械扫描尺寸是相当的,而在实际星载或机载SAR中实现一个百米甚至更高量级的SISO面阵是非常困难的,因此该成像体制常见于安检、医学成像等近场应用中。美国西北太平洋国家实验室(Pacific Northwest National Laboratory, PNNL)研制了世界首台毫米波全息成像系统,该系统通过天线机械扫描形成平面观测孔径,并结合宽频带信号实现对目标的三维成像,是扫描SISO面阵体制的典型应用[11]。
一些典型的SAR成像算法,包括频率变标算法[12](Frequency Scaling Algorithm, FSA)、线频调变标算法[13](Chirp Scaling Algorithm, CSA)、距离徙动算法[14](Range Migration Algorithm, RMA)等,经过简单推广即可用于扫描SISO面阵体制下的三维成像应用,特别是RMA因其对目标回波信号处理的高精度、高效率而被广泛应用于各种近场阵列成像体制中[15-17]。然而,典型RMA为了在回波信号处理过程中执行三维逆快速傅里叶变换(Inverse Fast Fourier Transform, IFFT)操作而引入了球面波的平面波近似以及距离维插值操作,这将造成一定的近似和插值误差,进而会导致一定的图像质量和分辨率的损失。文献[18]中提出了一种宽带积累方法,通过对不同空间波数对应的聚焦图像相干累加得到目标图像,有效避免了使用RMA带来的插值误差,然而该方法仍然对回波相位项执行了近似处理。因此,本文提出了一种基于FFT的扫描SISO面阵近场成像技术,首先考虑了目标回波沿空间路径的传输损耗,保留了回波模型中的幅度衰减因子,根据目标回波方程特性对方位维和高度维执行卷积操作,再通过FFT、降维和相干累加等步骤对回波进行处理得到最终的目标重构图像,同时避免了应用RMA带来的多步近似和插值误差造成的图像质量损失。仿真分析和实验结果表明,所提出的方法不仅可以在保证图像重构效率的前提下提升图像质量,还能够有效降低信号空间传播损耗对成像质量带来的影响。
1 成像方法推导及实施
扫描SISO面阵体制坐标系如图1所示,这里建立了笛卡尔坐标系,坐标圆心位于SISO面阵的中心位置,其中(x,y,0)表示面阵上的收发阵元位置,(x′,y′,z′)代表目标的空间三维坐标,因此x和y维度分别代表SISO面阵的方位维和高度维,阵列平面所在位置z=0。

图1 扫描SISO面阵体制坐标系Fig.1 Scanning SISO array coordinate system
这里默认系统发射信号为调频连续波,考虑到信号在空间中的传播衰减,在回波模型中保留了幅度因子1/R2,那么接收目标回波信号模型可以表示为:
(1)
式中:s(·)表示目标回波信号;σ(·)表示目标函数,即目标的像;k=2πf/c为空间波数,其中f和c分别表示空间频率和光速;R代表收发阵元到目标的距离。定义该距离表达式为:
(2)
这里定义
(3)
那么目标回波可重新表示为:
s(x,y,k)=∭σ(x′,y′,z′)·
F(x-x′,y-y′,z′,k)dx′dy′dz′
(4)
可以看出,式(4)为一个卷积积分表达式,那么式(4)可以变换成:
(5)
式中,“*(x,y)”表示对x、y两个维度的卷积。
对式(5)两端的x和y维度分别执行FFT操作可得到:
(6)
根据时域相关法的成像原理,得到目标图像的频域表达式为:
(7)
对于某一特定的目标所在距离维平面zi,都存在:
(8)
根据式(8),对于每一个空间波数kl都有:
(9)
对式(9)两端的kx和ky维度分别执行IFFT操作,可得到目标子图像表达式为:
(10)
最终重构出的目标图像表达式为:
(11)
式中,N和M分别表示重构空间目标所需距离维平面的个数以及空间波数数目。
于是基于FFT的扫描SISO面阵成像方法步骤如下:

步骤2:建立包含相位项的表达式F(x,y,z′,k),即:
(12)

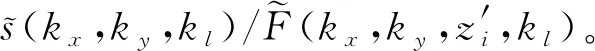


2 仿真及实测数据验证
本文应用了大量的仿真和实测数据对所提出的基于FFT的扫描SISO面阵成像方法的有效性进行了验证,成像几何形状与图1相同。成像算法是在配置为2.1 GHz处理器和8 GB内存的计算机上实现的。
2.1 仿真验证
本文开展了两组数值仿真来验证所提方法的有效性。为了验证所提方法的图像重构质量提升能力,采用的第一类目标为图2(a)所示的柠檬片模型,柠檬片直径为12.5 cm,厚度为2.5 cm,柠檬片几何中心到SISO面阵(即z=0平面)的距离为50 cm,应用FEKO电磁仿真软件进行几何建模并计算其目标回波,仿真频率范围为30~36 GHz,频点数M=31,天线阵列尺寸为50 cm×50 cm,阵元间隔为4.5 mm,符合阵元间隔Δx≤λ/2的阵列采样间隔要求,λ为中心频率对应的波长。
图2(b)和图2(c)分别为SISO-RMA和本文所提方法对柠檬片模型的三维图像重构结果,重构时间分别为1.33 s和1.05 s。在显示动态范围相同的条件下,对比两图可以看出,SISO-RMA对应的目标图像中柠檬片轮廓存在很多凸起,重构效果较差,而所提方法对应的重建图像中柠檬片轮廓更光滑,重构精度更高。
为了验证所提方法的信号传输损耗补偿能力,采用的第二类目标为图3(a)所示由理想散射点构成的空间分布的多点目标模型,天线阵列尺寸为40 cm×40 cm,计算所用频段、频点数和阵元间距与第一组仿真参数相同。

(a) 柠檬片模型(a) Model of lemon slice

(b) SISO-RMA重构结果(b) Reconstruction results of SISO-RMA
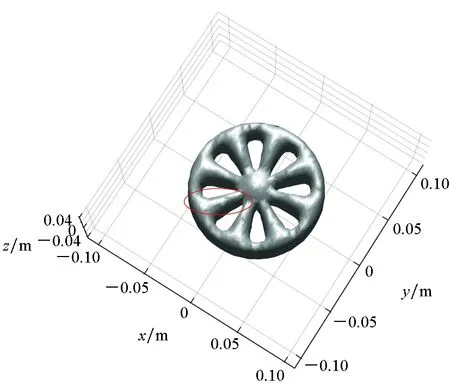
(c) 所提方法重构结果(c) Reconstruction results of the proposed method图2 仿真柠檬片模型成像结果Fig.2 Imaging results of simulated lemon slice model
图3(b)和图3(c)分别为SISO-RMA和本文所提方法对空间多点目标模型的三维图像重构结果,重构时间分别为2.83 s和4.06 s。在显示动态范围相同的条件下,对比两图可以看出,随着点目标与阵列平面距离增加,SISO-RMA对应的目标图像中点目标的像素强度逐渐变弱,尤其是z=0.6 m和z=0.7 m处的点目标已无法看到,相比之下,所提方法具有更好的信号传播衰减补偿性能。值得一提的是,虽然本文采用的SISO-RMA对应的成像结果都是经过距离向的幅度补偿后得到的,但由于在近场成像中重构区域在方位向、高度向以及距离向的跨度处于同一量级,因此仅对距离向的幅度衰减进行补偿无法有效降低信号空间传播损耗对成像质量带来的影响。
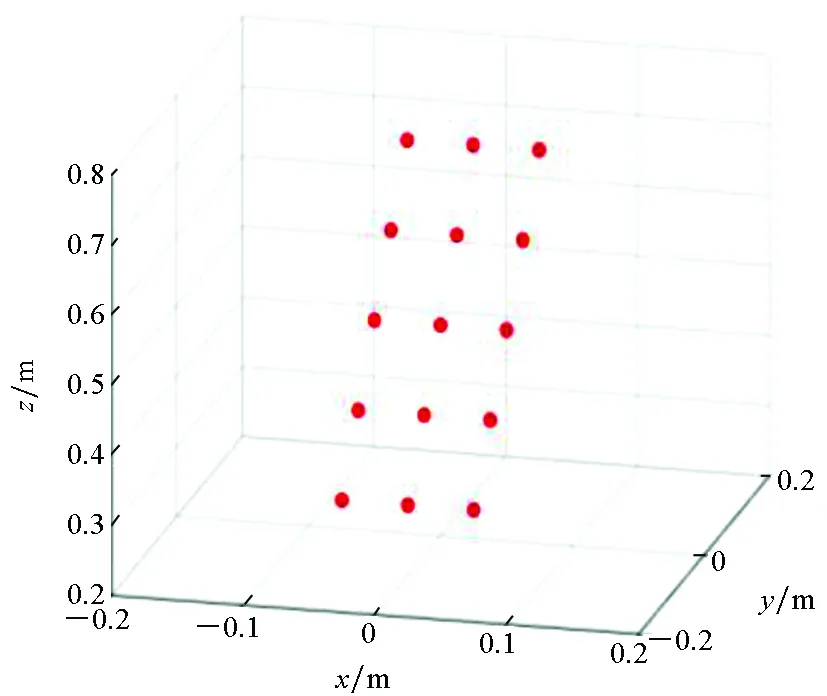
(a) 多点空间目标模型(a) Spatial target model of multiple points
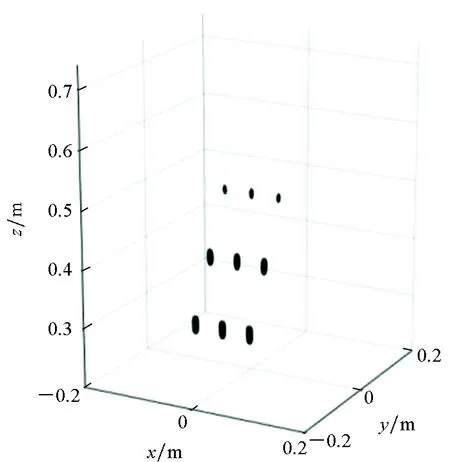
(b) SISO-RMA重构结果(b) Reconstruction results of SISO-RMA
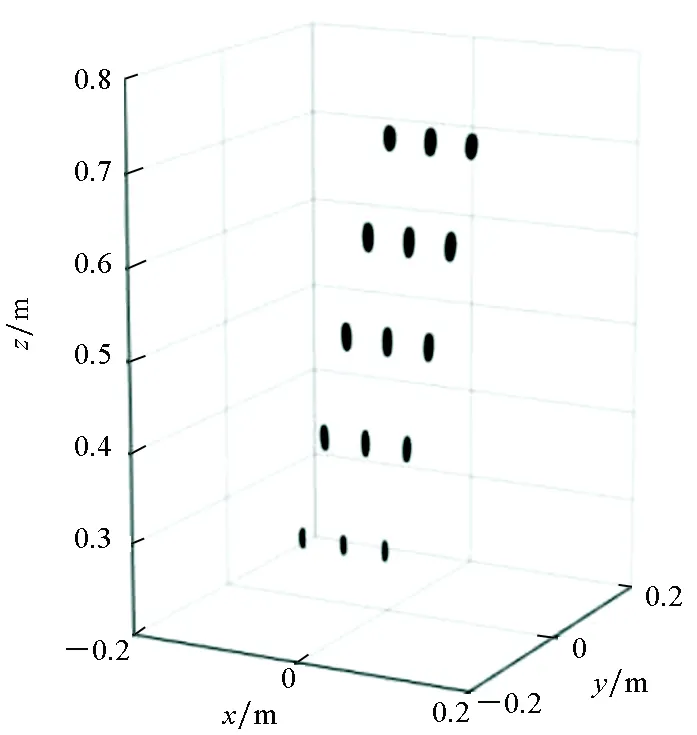
(c) 所提方法重构结果(c) Reconstruction results of the proposed method图3 空间多点目标模型成像结果Fig.3 Imaging results of the spatial target model of multiple points
2.2 实测数据验证
本文通过搭建相应的实验系统来模拟扫描SISO面阵体制,进而验证所提方法的有效性以及实际场景应用的可行性。实验的基本配置如图4所示,个人电脑(Personal Computer, PC)通过串口与控制器相连来控制二维扫描架运动,PC与矢量网络分析仪(Vector Network Analyzer, VNA)通过网线相连并控制其产生信号并读取目标回波数据。

图4 扫描SISO面阵实验基本配置Fig.4 Basic configuration of the scanning SISO array experiment
本文开展了两组实验来验证所提方法的有效性。为了验证所提方法的图像重构质量提升能力,采用图5(a)所示的人体模特作为成像目标。该模特腰部固定了一把仿真手枪模型,其所在距离维平面到扫描SISO面阵(即z=0平面)的距离为50 cm,在实验中设置VNA的工作频段为33~37 GHz,M=501,扫描孔径尺寸为64 cm×83.6 cm,扫描间隔为4 mm。
图5(b)和图5(c)分别为SISO-RMA和本文所提方法对实物模型的x-z平面投影图像重构结果,重构时间分别为22.34 s和8.79 s,在显示动态范围条件下,对比两图可以看出,两种方法都可以很好地重构人体背部和手枪模型轮廓,但所提方法对应的图像重构精度更高,而SISO-RMA对应的目标图像质量相对较差,无用的旁瓣成分较多,具体体现在图5(b)中红色圆圈包含的像素位置。
为了验证所提方法的信号传输损耗补偿能力,采用的成像目标为图6(a)所示的一个金属圆柱体和一个金属小球,采用成像场景的正视图和侧视图分别如图6(b)和6(c)所示,相比于阵列平面,金属圆柱体位于近处,金属小球位于远处,它们的几何中心在距离向上相距约33.5 cm,在实验中设置VNA的工作频段为30~36 GHz,M=101,扫描孔径尺寸为49.5 cm×31.5 cm,扫描间隔为4.5 mm。

(a) 实物模型(a) Physical model

(b) SISO-RMA重构结果(b) Reconstruction results of SISO-RMA

(c) 所提方法重构结果(c) Reconstruction results of the proposed method图5 实物模型成像结果Fig.5 Imaging results of physical model
图7(a)和图7(b)分别为SISO-RMA和本文所提方法对位于不同距离的金属圆柱体和金属小球在高度维的最大值投影成像结果,重构时间分别为3.60 s和10.58 s。在显示动态范围相同的条件下,从成像结果中可以看出,SISO-RMA对应的成像结果中与阵列平面相距较远的小球几乎消失不见,相比之下,所提算法的距离补偿性能要更好。

(a) 成像目标(a) Imaging target

(b) 成像场景正视图(b) Front view of the imaging scene

(c) 成像场景侧视图(c) Side view of the imaging scene图6 成像目标与成像场景Fig.6 Imaging target and imaging scene

(a) SISO-RMA重构结果(a) Reconstruction results of SISO-RMA

(b) 所提方法重构结果(b) Reconstruction results of the proposed method图7 实物模型成像结果Fig.7 Imaging results of physical model
3 结论
本文提出了一种基于FFT的扫描SISO面阵近场成像技术,该技术通过保留回波模型中的幅度衰减因子,并根据目标回波方程特性对目标回波以及包含幅度因子的相位项中的方位维和高度维执行卷积操作,最后应用FFT、降维以及相干累加等步骤对回波进行处理得到最终的目标图像。仿真分析和实测数据表明,应用该技术重构目标图像不仅避免了应用SISO-RMA带来的近似和插值误差,并且可以在保证图像重构效率的前提下提升重构质量,重要的优势是该方法还能够有效降低信号空间传播损耗对成像质量带来的影响。值得一提的是,在本文所提方法中可以进一步对所有空间波数以及距离向平面组合执行并行计算操作,这样可显著提升成像效率,进行实现实时成像。

