挠性航天器变幅值输入成形姿态机动策略 *

王 杰，吴 军，邹 杰

(国防科技大学 空天科学学院， 湖南 长沙 410073)

随着一些大型柔性部件(如太阳翼、天线或散热器等)在现代航天器上得到应用，航天器呈现出复杂的刚柔耦合特征。特别是当航天器进行姿态机动时，将激起柔性附件显著的弹性振动，且反作用力矩作用于航天器平台上，引起平台的姿态抖动，对于执行对地观测、激光通信等高精度任务的航天器是一个严峻的挑战。

此外，在执行一些任务时，航天器上挠性结构相对于本体需要做大范围刚体运动。比如：为持续获取电能，太阳电池阵需要持续跟踪太阳；航天器完成姿态机动任务后，要求电池阵快速指向太阳，以在机动期间或机动之后进行工作。在一些情况下，天线也需要连续指向目标。挠性结构相对于航天器本体做刚体运动，会导致系统动力学参数发生变化，航天器呈现时变参数特性，且航天器姿态在三个方向上的动力学特性会相互耦合，给姿态机动路径的设计和姿态的稳定带来了新的难题。

在近三十年的发展过程中，相关学者在航天器机动控制方面作出了重要的贡献。其中输入成形方法[1]广泛应用于柔性航天器的姿态机动规划。该方法通过调整航天器姿态机动时的脉冲序列，使机动后柔性系统的残余振动最小。为进一步提高方法的鲁棒性，相继提出一些高阶方法如零振动和零微分(Zero Vibration Derivative, ZVD)成形方法、极不灵敏度(Extra Insensitive, EI)成形方法[2]、特定不灵敏度(Specified Insensitivity, SI)成形方法[3]等。在国内，1987年最早提出了分力合成的基本理论，与输入成形方法本质上是相同的[4]。在多模态系统中，输入成形算法设计过程中考虑系统多阶固有频率和振型[5-6]。在航天器姿态机动领域，首先获取系统典型的固有频率和模态阻尼比，然后采用输入成形方法设计合适的机动路径或控制输入曲线。Parman[7]结合输入成形方法和比例-微分(Proportional Derivative, PD)控制提出了一种闭环控制策略，用于含柔性太阳能帆板的航天器姿态机动。Zhang等[8]将输入成形方法应用于柔性航天器的快速姿态机动中。Singh等[9]提出了采用两脉冲和三脉冲的成形器，以进一步提高鲁棒性，但该方法不能在线调整参数。胡庆雷等[10]结合滑模控制与输入成形方法提出了一种挠性航天器姿态机动的方法，使闭环系统取得更优的性能。

之后，学者发展了自适应输入成形理论[11]，其成形器的参数可在线调整，具有更强的鲁棒性，适用于参数快变或未知的系统。Orszulik等[12]针对参数未知的系统，采用最小二乘法进行估计，基于输入成形法控制柔性结构的振动。此外，输入成形理论也已应用于强非线性的系统[13-14]。对于参数在一定范围内变化的系统，Magee等[15]设计了一种改进的输入成形器，用于变频率系统的控制。Pao等[16]对比了几种传统成形器与变幅值成形器的性能，数值仿真结果表明变幅值成形器能更好地适应具有建模偏差、频率摄动的系统。Cho等[17]针对工业机器人系统的周期时变问题，基于状态转移矩阵计算时变输入序列，开展了地面实验进行验证，但忽略了模态之间的耦合。Lee等[18]基于模态滤波冲击响应的思想方法提出了一种改进的成形器，在参数变化较快的系统中得到了验证。Otsuki等[19]提出了一种鲁棒输入成形策略，同时控制柔性结构的位置和振动。针对单输入单目标系统，提出了一种综合的设计方法，不受系统参数变化的影响，并用于火星车的控制[20]，但该方法不适用于多目标系统。

前面的研究大多针对不确定系统或变频系统，研究变参数挠性航天器姿态机动的工作未见报道。在文献[21]中，作者首先针对变参数二阶振动系统，设计了变幅值零振动(Zero Vibration, ZV)输入成形器，提出了一种基于变幅值输入成形的航天器姿态优化方法。然而，该方法对柔性结构的动力学参数(固有频率和阻尼系数)较为敏感，在动力学参数存在误差时，柔性结构的残余振动较为明显。因此，本文提出了鲁棒输入成形器的设计方法，并以此构造了变参数挠性航天器的鲁棒姿态机动路径优化方法。该方法在变幅值ZV成形器的基础上，提高成形器的阶次，构造线性约束条件使存在参数不确定性的系统柔性结构残余振动为零，提高了控制系统的鲁棒性。

1 挠性航天器数学模型

图1给出了一个典型的挠性航天器的示意图。航天器包含一个代表卫星本体的中心刚体，带有一个或多个柔性铰接附件，表示星载天线、太阳翼或其他柔性结构。由于中心刚体与柔性附件之间的耦合，航天器经历三轴姿态机动时，会激起柔性附件的振动，而柔性附件的振动将会影响中心刚体的姿态角速度和指向精度。

图1 含柔性铰接附件的航天器Fig.1 Spacecraft with flexible movable appendage

基于伪拉格朗日方程，系统的动力学方程可表示为：

(1)

其中：第一个方程为航天器姿态运动控制方程，第二个方程为柔性附件的弹性振动方程。J为航天器转动惯量矩阵，为中心体和挠性附件的惯量之和；ω为中心刚体的角速度矢量，τ为作用于航天器上的控制力矩，C为刚柔转动耦合矩阵，η为挠性附件模态坐标，ξ为挠性附件阻尼比矩阵，Λ为附件自然频率矩阵。由于有刚柔转动耦合矩阵，姿态运动与弹性振动耦合在一起。柔性附件固定于航天器上时，系统为定常系统，动力学参数不随时间变化；而当柔性附件相对于航天器本体发生刚体运动时，柔性附件的转动惯量在航天器本体坐标系中不断变化，矩阵J和C为时变参数，系统为时变系统。

对于参数不变或在小范围内变化的系统，在得知航天器系统频率和阻尼系数的情况下，采用经典的输入成形方法设计姿态机动路径，机动完成后柔性附件的残余振动为零。而对于参数大范围变化的系统，该方法不适用。

2 变幅值鲁棒成形器

一般地，对于参数存在不确定性的系统，可提高成形器的阶次，以提高控制系统的鲁棒性。在变幅值ZV成形器的基础上，本节提出变幅值ZVD成形器设计方法。

给定一二阶线性系统

(2)

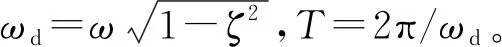
图2所示为ZVD成形器原理，成形器由作用于0、T/2和T时刻的三个脉冲信号组成。成形后的信号的时间历程为tf+T。

(a) 参考信号(a) Reference Signal (b) 脉冲序列(b) Impulse Sequence图2 ZVD成形器原理图Fig.2 Schematic of ZVD input shaper

三个脉冲信号的幅值满足：

(3)

式中，i=1,2,3，且

(4)

与ZV成形器相比，ZVD成形器对参数不敏感。

基于ZVD成形器的设计思想，设计了变幅值ZVD成形器。假设二阶系统的周期T满足T=m·(tf/n)，(m∈+，m为偶数)。同时将机动时间分为n(n∈+)份，每份满足条件Δt=tf/n。

外载荷或控制力可离散为一系列的脉冲。

=f1(t)·δ(t-t1)+f2(t)·δ(t-t2)+…+

fm(t)·δ(t-tm)+fm+1(t)·δ(t-tm+1)+…+

fn(t)·δ(t-tn)

(5)

式中：fi(t)为第i个输入元；ti为第i个脉冲的延迟时间，且ti= (i-1)·Δt。

将相差半周期整数倍的输入元组合，定义为一向量

(6)

j=1,2,…,m/2;l=1,2,…,k-2

(7)

(8)

(9)

(10)

即

(11)

将式(9)代入式(11)，可得：

(12)

3 变幅值输入成形姿态路径规划方法

本节提出一种时变输入成形控制方法，重新规划航天器的姿态机动路径，保证机动后附件的残余振动最小。简单起见，考虑航天器姿态机动为rest-to-rest机动，在机动前和机动后，航天器姿态角分别为θ0和θend，机动前后航天器姿态角速度均为0。

3.1 非线性约束条件

采用非耦合线性模型设计bang-bang机动策略，即姿态角加速度变化趋势为bang-bang类型。航天器首先加速然后减速，加速时，角加速度为a0= [ax,0,ay,0,az,0]T，反之减速时角加速度为-a0。对姿态角加速度进行无量纲化处理。

(13)

式中，χx、χy、χz为无量纲系数，与姿态角速度的关系可表示为：

(14)

对于bang-bang输入，χ满足：

(15)

式中，i=x,y,z。

四元数矢量对时间的导数满足：

(16)

式中

(17)

控制输入需保证获得与bang-bang机动策略所导致的姿态角变化一致。将方程(16)离散，即

(18)

时刻t=iΔt的姿态四元数Q为：

(19)

定义t=iΔt时刻到t=(i+1)Δt时刻四元数向量的状态转移矩阵为：

(20)

可得末端时刻和初始时刻四元数的状态转移矩阵为：

(21)

应该满足：

Qend=T0→nQ0

(22)

上述约束条件保证了成形后的控制输入所导致的航天器欧拉角变化与bang-bang机动后的姿态角相等。

3.2 线性约束条件

(23)

该系统为二阶系统，通过输入成形方法构造控制输入。系统中存在时变项，需要改进传统的输入成形方法。基于航天器的刚体模型根据姿态机动目标和机动时间求解角加速度的参考路径a。为减小甚至消除式(23)系统的残余振动，基于输入成形思想对参考路径进行重新规划。将机动时间ta均分为n段，时间间隔为Δt，在每个时间间隔中将时变系统进行线性化处理，惯量矩阵和耦合矩阵为常值。

同时，在每个间隔中，控制输入也为常值，分段线性系统的控制输入为分段的。二阶系统的前N阶模态周期表示为T1,T2, …,TN，(T1>T2>…>TN)。假定满足条件：

(24)

与定常参数系统相比，时变系统的加速时间保持不变，仍假定为ta。在第i(i=1,2,…,n)个间隔(t∈[(i-1)Δt，iΔt])内，外载荷或控制力为常值，可表示为：

(25)

控制力分解为：

F(t)=F1·δ(t-t1)+(F2-F1)·δ(t-t2)+…+

(Fm-Fm-1)·δ(t-tm)+…+

(Fm+1-Fm)·δ(t-tm+1)+…+

(Fn-Fn-1)·δ(t-tn)

(26)

定义

(27)

3.3 优化问题定义

为减小系统控制输入的脉冲性，定义平滑函数为：

(28)

因此，问题为在约束条件(27)和条件(22)下求解χ。定义优化问题：

(29)

由于存在非线性约束条件(22)，采用序列二次规划算法求取χ的最优解，然后计算最优机动路径和控制力矩。

4 数值仿真

4.1 仿真对象

为验证上节提出的方法的有效性。本节采用一含星体和柔性太阳翼的航天器的机动过程进行说明[22]。航天器包含一对太阳翼，每侧太阳翼均由铝合金三脚架和碳纤维电池阵组成，三脚架通过太阳翼驱动机构(Solar Array Drive Assemblies, SADA)和航天器本体铰接，三脚架以角速度Ω绕xs轴旋转。γ为航天器本体坐标系oxyz与惯性系OXYZ之间的夹角，初始时刻两个坐标系重合。航天器本体转动惯量为diag [2 666.7, 2 666.7, 1 666.7]kg·m2。单侧太阳翼相对于浮动坐标系的转动惯量为diag [53.6, 1 607.9, 1 661.6]kg·m2。分析中不考虑太阳翼的材料和结构阻尼。

简单起见，仅考虑太阳翼的前6阶约束模态(即太阳翼根部固支求得的模态)，见表1。

航天器本体姿态与太阳翼模态坐标的刚柔转动耦合矩阵为：

(30)

表1 太阳翼约束模态和频率

由耦合系数矩阵C可以看出，xs向扭转模态与x向姿态角速度ωx耦合。当太阳翼转角γ为0°或180°时，y向姿态角速度ωy与ys向弯曲模态耦合，z向姿态角速度ωz与zs向弯曲模态耦合。当转角γ为90°或270°时，y向角速度只与zs向弯曲模态耦合，z向姿态角速度只与ys向弯曲模态耦合。在太阳翼位于其他角度时，这两个方向的角速度和弯曲模态相互耦合。

4.2 仿真结果

航天器进行三轴姿态机动，初始时刻航天器欧拉角和姿态角速度均为[000]T，机动后航天器欧拉角目标值为[60°, 45°, 30°]T，姿态机动时间设定为20 s。太阳翼绕xs轴以Ω=3 (°)/s的角速度旋转，初始时刻γ为0°。

(a) y向(a) y-direction

(b) z向(b) z-direction图3 成形器控制力矩对比Fig.3 Comparison of torques between two input shapers

(a) y向(a) y-direction

(b) z向(b) z-direction图4 两种成形器航天器本体姿态角速度对比Fig.4 Comparison of angular velocities between two input shapers

图3给出了采用变幅值ZV和ZVD两种成形器情况下的控制力矩输入曲线，图4和图5分别给出了航天器本体姿态角速度和姿态角响应曲线。由图3～5可知，两种成形器均能实现控制目标。图6给出了太阳翼顶端面外位移响应。由图6可得，姿态机动过程中，柔性太阳翼的弹性振动幅值较大，机动完成后，太阳翼残余振动很小，达到了输入成形的目的。

图5 两种成形器航天器姿态角变化曲线Fig.5 Comparison of attitude angles between two input shapers

图6 两种成形器太阳翼顶端面外位移响应对比Fig.6 Comparison of tip deflection between two input shapers

4.3 鲁棒性分析

现实系统中，建模存在误差，并不能准确地获取系统的频率、阻尼系数等参数。因此本节中对固有频率和阻尼系数进行摄动，以评估建模误差和系统参数变化结果的影响。定义太阳翼固有频率摄动系数ε=|1-(ωact/ωnom)|，ωact为频率实际值，ωnom为用于成形器设计的固有频率标称值。分别计算ε为5%和10%时，机动过程中太阳翼的第一阶模态坐标的响应过程，如图7所示。图8为ε=5%时太阳翼顶端面外位移响应。图9对比了在频率存在偏差时两种成形器下航天器姿态角响应。可以看出，由于ZV成形器后，太阳翼仍存在较大的残余振动，导致航天器本体姿态角速度呈现非零振荡现象，航天器姿态角逐渐偏离目标值。变幅值ZVD成形器对误差具有更好的不敏感性，鲁棒性更强。

(a) ZV成形器(a) ZV shaper

(b) ZVD成形器(b) ZVD shaper图7 频率摄动对第一阶模态的影响Fig.7 Responses of the first modal coordinate with frequency perturbation

(a) 全局图(a) Complete time history

(b) 局部放大图(b) Zoomed portion图8 太阳翼顶端面外位移响应对比(ε=5%)Fig.8 Comparison of tip deflection (ε=5%)

图9 航天器姿态角变化曲线(ε=5%)Fig.9 Comparison of attitude angles (ε=5%)

(a) 全局图(a) Complete time history

(b) 局部放大图(b) Zoomed portion图10 阻尼不确定性对太阳翼第一阶模态坐标的影响 (ZV 成形器)Fig.10 Responses of the first modal coordinate with damping uncertainty (ZV shaper)

(a) 全局图(a) Complete time history

(b) 局部放大图(b) Zommed portion图11 阻尼不确定性对太阳翼第一阶模态坐标的影响 (ZVD 成形器)Fig.11 Responses of the first modal coordinate with damping uncertainty (ZVD shaper)

(a) 全局图(a) Complete time history

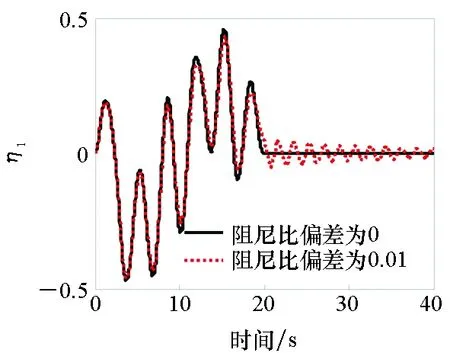
(b) 局部放大图(b) Zoomed portion图12 阻尼比为0.01时太阳翼顶端面外位移响应对比Fig.12 Comparison of tip deflection with damping uncertainty is 0.01

实际系统的阻尼比很难得到准确值，因此在求解航天器姿态最优姿态机动路径时，太阳翼的模态阻尼比视为0，需要考虑本文所提出的成形器对系统阻尼系数误差的鲁棒性。计算实际系统阻尼比偏差为0.01(即阻尼比为0.01)时姿态机动路径优化算法的鲁棒性。图10和图11给出了两种成形器下第一阶模态坐标的动力学响应曲线，图12中给出了太阳翼的顶端位移响应曲线。在存在阻尼系数不确定性的情况下，采用变幅值ZV成形器时，机动后太阳翼的残余振动显著增大，而采用变幅值ZVD成形器时，太阳翼的残余振动保持较低的幅值，因此ZVD成形器对阻尼系数不确定性的鲁棒性明显增强。

5 结论

针对挠性航天器系统参数不确定的情况，本文提出了变幅值ZVD成形器设计方法，并相应地提出了鲁棒性强的最优变幅值输入成形姿态机动策略，仿真分析了系统存在频率偏差和阻尼系数不确定性时该机动策略的鲁棒性。取得的主要结论如下：

1)提出的鲁棒最优变幅值输入成形姿态机动策略，可使航天器在姿态机动的同时，激起的挠性结构的弹性振动幅值较小，因此可显著地改善机动后航天器的指向精度和稳定度。

2)当挠性结构固有频率摄动5%时，采用变幅值ZV成形器设计姿态机动路径，机动完成后残余振动较大；而采用鲁棒变幅值成形器，太阳翼残余振动很小。

3)当挠性结构模态阻尼比偏差为0.01时，变幅值ZV成形器对阻尼系数偏差较为敏感，而鲁棒变幅值成形器几乎不会增大太阳翼的残余振动幅值。

仿真结果表明，本文提出的鲁棒姿态机动路径设计方法具有优异的鲁棒性和稳定性。