基于实时变量逆矩阵求解的非线性MIMO 解耦ADRC 控制方法*

随博文，黄志坚

（上海海事大学商船学院，上海 201306）

0 引言

多输入多输出（MIMO）控制系统，即多变量系统，广泛用于工业领域。与单输入单输出（SISO）控制系统不同，多输入多输出控制系统往往由许多测量和控制信号组成，且各变量之间具有复杂的耦合关系，这给实际应用带来很大困难。通过某种方法，将多变量系统的输出分解为单个独立的输出，这种方法通常称为解耦［1-2］。变量之间交互作用的强弱是衡量系统控制难度的一个指标。对于强耦合系统，解耦控制是较为有效的解决方法。自抗扰控制器作为一种不依赖精确数学模型、具有较强的适应性和抗扰动能力的控制策略，适合用于解决解耦控制面临的问题。通过线性扩张状态观测器，可以将回路间耦合、模型不确定性、扰动等当作总的扰动，进行估计并通过控制规律补偿。传统的解耦方法通过求解逆矩阵来实现。在这种方法中，求解控制矩阵的逆矩阵显然是首要问题。

近年来，研究者们提出了一类数值方法，如蒙特卡罗法、迭代法等［3-5］。文献［3］提出了一种求解矩阵求逆的迭代算法。文献［4］采用牛顿迭代法求取矩阵的逆矩阵，与神经网络方法相比。虽然迭代数值方法对矩阵求逆有一定的效果，但其缺点是处理大规模数据的复杂度很高［6-7］。文献［7］提出了一种基于蒙特卡罗方法来求解一类矩阵的逆矩阵方法。虽然迭代数值方法对矩阵求逆是可行的，但它们在处理大规模数据时具有复杂度高的缺点［8-9］，如计算量大、计算时间长。

随着对神经网络的进一步研究，基于神经网络求解逆矩阵的方法开始出现。与传统的数值方法相比，神经网络具有并行处理、分布式存储、硬件实现等优点［9-11］。文献［12］使用了一个由奇数激活函数构造的基于梯度的神经网络系统来求解矩阵的逆。文献［13］提出了一种基于非线性演化公式的有限时间收敛神经网络来求解时变矩阵的逆问题，它能在有限时间内收敛并精确地达到理论解。此外，神经网络方法不仅可以求解实数域的逆矩阵，而且可以通过变换方法求解复杂域的逆矩阵［14-19］。文献［19］提出了3 种不同的神经网络（ZNN）模型求复数域中时变矩阵的逆，仿真结果验证了这些模型的有效性。Wang 等［20］提出了两个具有不同激活函数的复数域ZNN 模型，以找到时变Drazin 逆，这两种模型都能在有限时间内收敛。文献［21］提出了一个复杂的变参数ZNN 模型来处理时变复数Sylvester 方程的逆问题。然而，该方法首先需要数据收集，训练模型并用基于神经网络的方法求解逆矩阵。

本文中，使用矩阵分解方法求解逆矩阵可以有效地克服上述问题。随着大数据时代的到来，本文提出了一种基于高斯消元法的LU 矩阵分解方法来求解矩阵逆问题，对求逆矩阵问题进行了分析。然后将该问题归纳为二阶、三阶、非方阵和时变测量信号的逆矩阵或高阶矩阵，并给出了它们的求逆矩阵的方法。对于被测信号变量或高阶矩阵，本文提出了一种基于高斯消去法，该方法通过将复杂矩阵分解为简单矩阵，降低了求解逆矩阵的难度，能快速得到求解结果，并且该方法可以借助计算机和Matlab 软件轻松地求解分解矩阵的逆矩阵。此外本文采用二输入二输出耦合系统的例子用于测试逆矩阵方法及其在解耦ADRC 控制中的作用。仿真结果表明，利用所提出的逆矩阵方法和解耦的ADRC 控制器信号，可以快速控制系统达到其平衡点。

因此，本文提出了一种的求解逆矩阵的方法，用于测量信号变量或高阶矩阵的求逆。该方法不仅简单，而且可实现实时控制的效果。另外，这种方法具有较为充分的数学理论和完成了非线性MIMO解耦ADRC 控制的理论和方法，提出了一种可用的非线性MIMO 解耦控制方案。此外，与其他求解逆矩阵方法相比，该方法具有以下特点：1）它可以准确有效地求解大规模矩阵的逆问题。2）对于被测信号为时变矩阵的问题，该方法也具有较好的效果。3）与神经网络方法相比，该方法不需要数据采集，训练或额外的学习过程。因此，该方法适用于数据驱动的非线性在线解耦控制。

1 非线性多输入多输出自抗扰控制解耦方法

1.1 自抗扰控制

自抗扰控制［22-23］是由韩京清教授首次提出的一种反馈控制方法，它保留了经典PID 的基本框架并作了4 个方面的改进：安排过渡过程的装置；提取系统状态信息（TD）和扰动总和信息的扩张状态观测器装置（ESO）；用状态误差信息来产生非线性误差反馈控制量的装置；根据扰动估计值对系统进行扰动补偿而生成最终控制量的补偿装置［24-25，27］。自抗扰控制器的结构图如图1 所示。

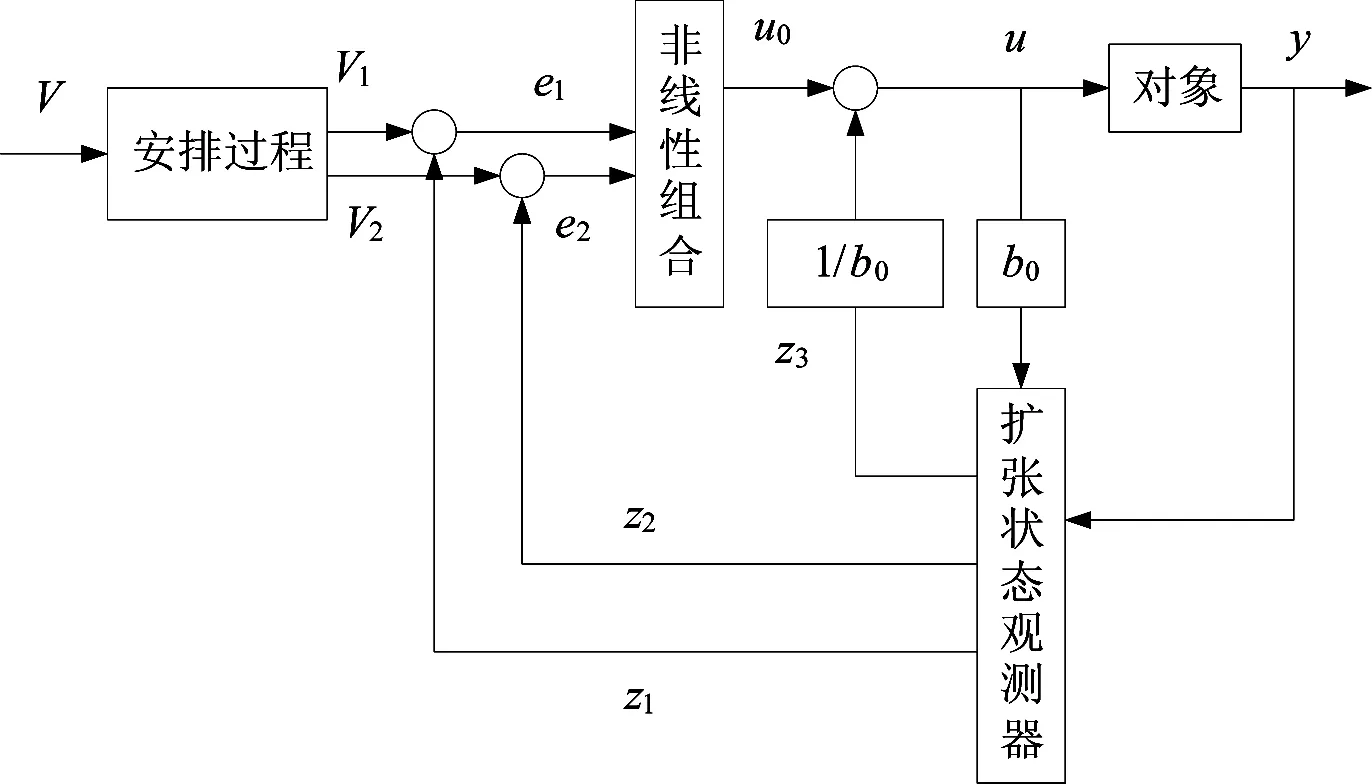
图1 ADRC 控制结构图

1）安排过渡过程，利用跟踪微分器（TD）提取微分信号：其中，fhan 和fal 是构造的非线性函数；vi1，vi2分别是系统状态和它的一阶微分；i 是下标为i 的ADRC 控制器；h 是指离散的时间采样步长；yi*是被控量的目标设定值；r 是系统的时间尺度；h0是过滤因子；e 是估计状态和系统输出的误差；yi是系统输出；zi1，zi2，zi3是扰动估计值；β01，β02，β03和β1，β2是增益系数；u是控制输出；α1，α2，δ1是fal 方程中的参数；b0是控制输出的补偿因子［21］。

1.2 非线性多输入多输出系统自抗扰控制

设有如下的多输入-多输出系统：

在这个系统中的第i 通道的输入输出关系为：

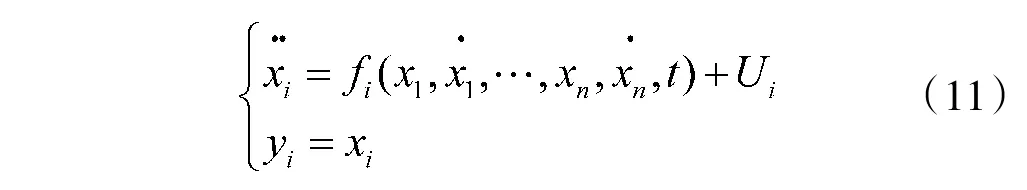
即第i 通道上的输入为Ui，而其输出为yi=xi，这样每一个通道的虚拟控制变量Ui与被控输出yi之间是单输入-单输出关系，即第i 通道的被控输出yi和虚拟控制变量Ui之间就被完全解耦了［1，20-21］。解耦原理如图2 所示。

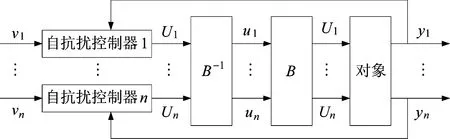
图2 非线性MIMO-ADRC 解耦控制原理图

1.3 逆矩阵变换分析

根据上述理论，可以看出式（6）中的矩阵B（x，x˙，t）应是可逆的，并且在非线性MIMO 自抗扰解耦过程中，应避免该矩阵为奇异矩阵。然而，在许多实际情况下，被控对象模型及其控制变量系数往往是未知的，只能通过把它作为可调参数来调整出其真值附近的值来用。大量仿真研究表明，对参数B（t）的估计值精度要求并不高，相对误差在30 %之内不会影响控制效果。因此，即使矩阵B（x，x˙，t）在系统运行过程中瞬间地出现不可逆的奇异现象也关系不大，可以在矩阵B（x，x˙，t）附近找一个可逆矩阵来近似即可。对于因矩阵系数为零的奇异矩阵，矩阵系数也可以在不超过30 %范围内变化，以此避免奇异现象的出现。并且这只会影响控制信号u（t）的能量大小，并不会影响ADRC 控制器的最终控制效果［22］。

此外系数矩阵B（t）主要随时间变化，因此，矩阵B（t）是一个可以被实时测量的信号变量矩阵。对于此类问题，常规用于求解实数型矩阵的求解逆矩阵的方法不再适用。在这种情况下，通常只有一般的变量迭代法才能求解逆矩阵。因此，本文提出了一种基于高斯消元法求逆矩阵的方法，该方法可以求解被测信号变量的逆矩阵，不需要控制对象模型等条件的约束。

2 逆矩阵的求解方法

逆矩阵的求解在工程实践中起着重要的作用。对于低阶矩阵而言，如二阶或三阶矩阵，有一些常规的逆矩阵求解方法，如定义法、伴随矩阵法以及矩阵变化法等。

对于高阶变量矩阵，这些常规的求解方法并不能很好地解决问题。因此，本文提出一种基于高斯消元法的矩阵分解的求解逆矩阵方法，这种方法不仅可以快速求解高阶矩阵的逆矩阵，而且可以求解时变矩阵的逆矩阵。

2.1 二阶、三阶矩阵的求逆方法

定义1.如果存在矩阵A，B，使得AB=BA=E，其中E 是单位矩阵，那么称A 矩阵可逆，并且有A-1=B。

因此，二阶或三阶矩阵的逆矩阵求解是有确定求解方式的，它们可以直接用方程式（13）和方程式（14）求得结果，可以避免使用中间数据进行运算，减少了计算量。

2.2 非方阵矩阵的求逆方法

，

这个广义逆求解法是另一种可用的方法。因此，非线性MIMO 解耦ADRC 方法可以用于更一般形式的状态变量方程。

2.3 变量矩阵和高阶矩阵的求逆方法

对于变量高阶矩阵，上述矩阵变换结果不能用于求解其逆矩阵。因此，本文提出了一种基于高斯消元法的LU 矩阵分解求逆方法，有效地解决此类的逆问题。

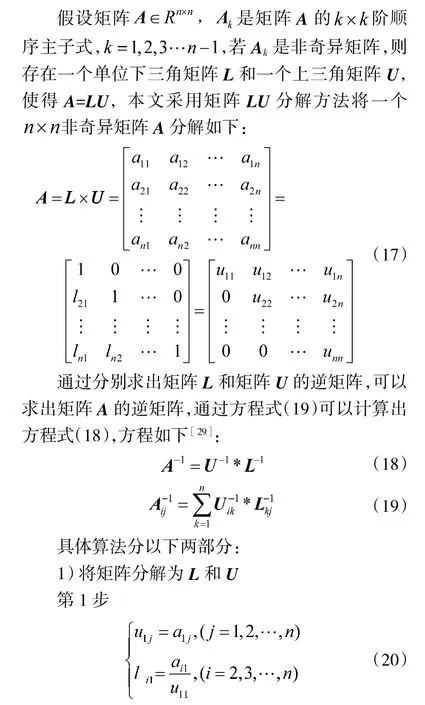
第2 步

通过这种方法，只要矩阵变量可以测量或估计，就可以用多项式计算求解逆矩阵。因此，该方法适用于实时求解被测信号变量或高阶矩阵的逆问题。

3 仿真结果与分析

通过一个数值例子的仿真说明该方法的有效性。假设一个非线性二输入二输出系统公式如下：

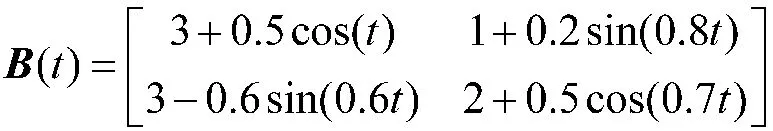
根据式（27），系数矩阵的变化图如图3 所示。

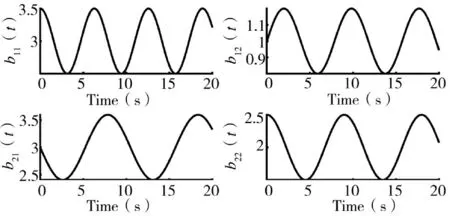
图3 耦合矩阵B（t）求逆前，控制输入系数b11（t），b12（t），b21（t），b22（t）随时间变化曲线

根据式（17）～式（24）中的矩阵分解求逆方法，可计算出耦合矩阵B（t）的逆矩阵：

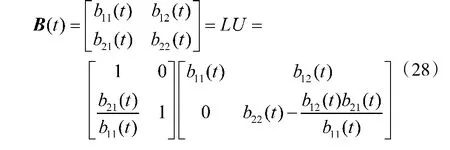
则B（t）的逆矩阵：

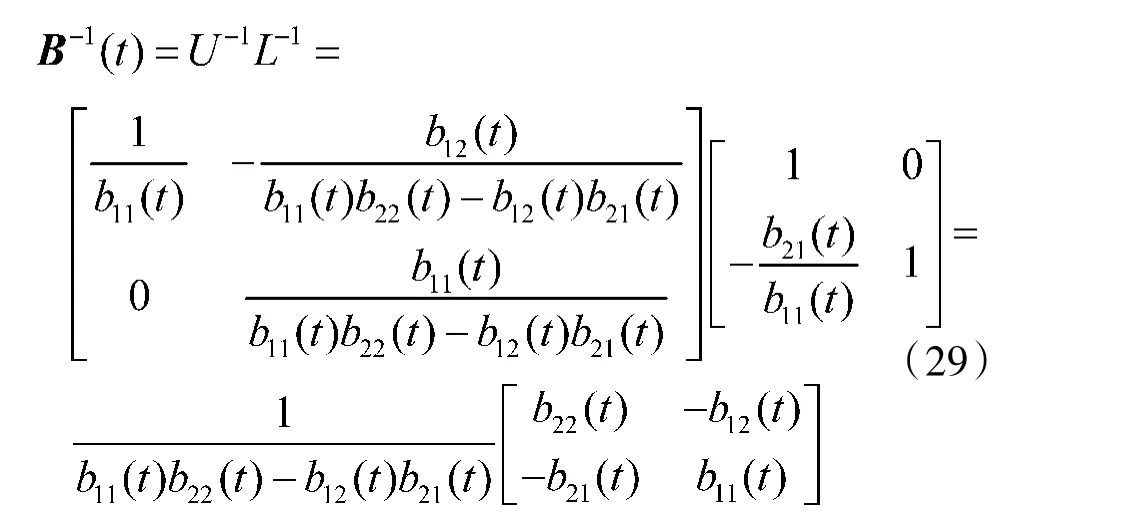
然后，将变量代入式（28），耦合矩阵B（t）的逆矩阵变化如图4 所示。

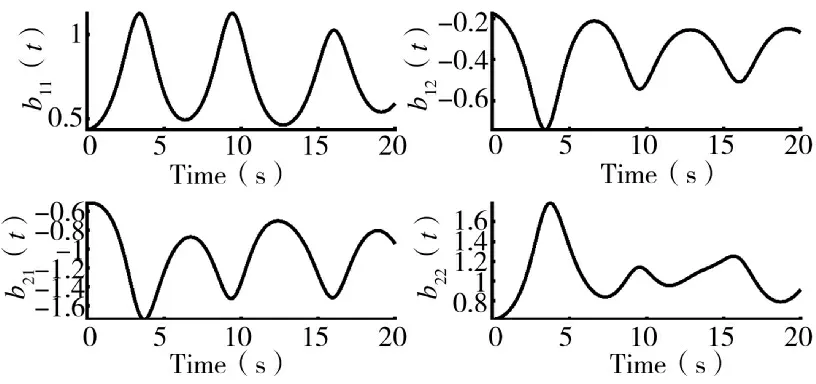
图4 通过矩阵分解求解B（t）逆矩阵时，控制输入系数b11（t），b12（t），b21（t），b22（t）随时间变化曲线

根据式（14）中的二阶矩阵求逆方法，可计算出矩阵B（t）的逆矩阵：

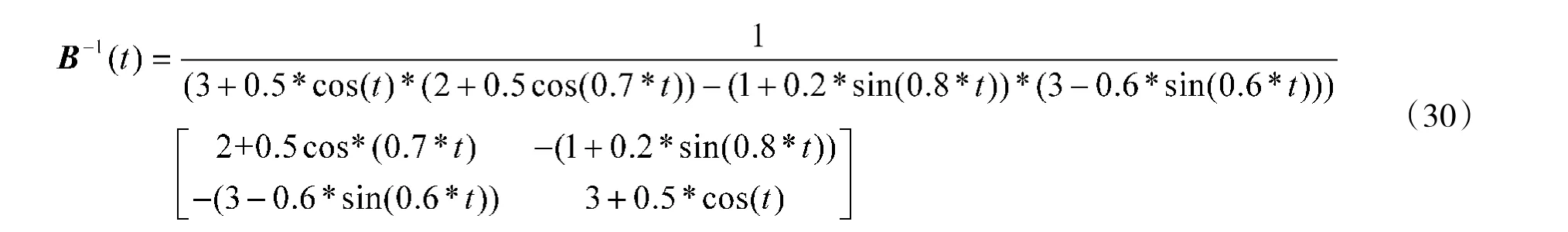
矩阵B（t）在求逆时内部元素变化曲线图如图5所示。

行列式bb 随时间的变化曲线如图6 所示。

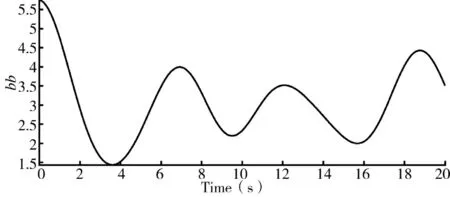
图6 耦合矩阵的行列式bb 随时间的变化曲线

从图4 和图5 可以看出，通过矩阵LU 分解求逆和式（14）方法求逆，两者的系数矩阵B（t）中的元素变化曲线是相同的，这也从另一方面证实了式（29）方法的正确性和有效性。将耦合矩阵B（t）通过矩阵LU 分解求逆后，就能够很好地解决式（26）、式（27）中的二输入二输出的非线性自抗扰解耦控制问题。通过设置不同的初始状态，进一步验证控制信号的稳定性和有效性。

1）初始系统状态设为x=［0，0］

将初始系统状态设为x=［0，0］，进行仿真实验，在仿真过程中，系统状态变量x（t）随时间的变化曲线如下页图7（a）所示，控制变量u（t）随时间的变化曲线如图7（b）所示。仿真实验表明，系统的状态变量在短暂波动后迅速收敛到目标设定值，利用本文所提方法可以快速实现式（26）二阶自抗扰控制的解耦问题。仿真图像表明，状态变量和控制变量都可以快速收敛，从而证明了本文方法的有效性和可行性。

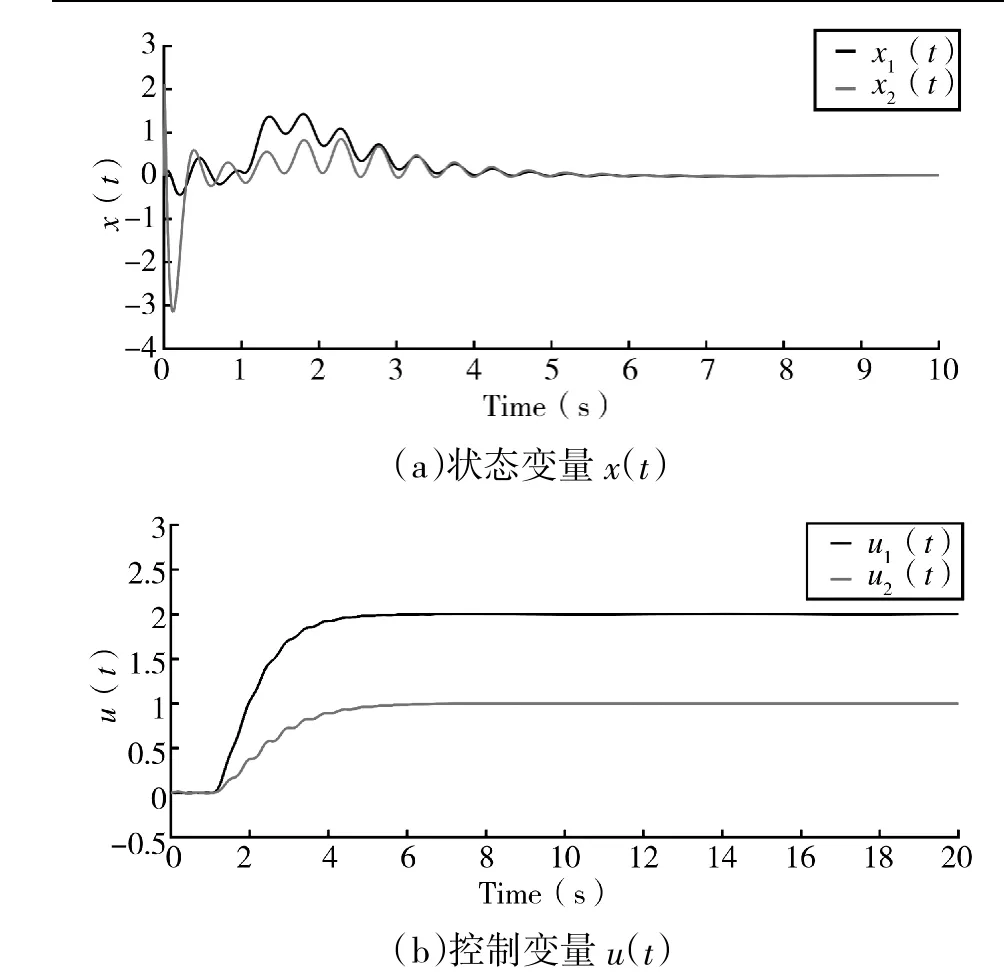
图7 系统初始状态为［0，0］收敛曲线

2）初始系统状态设为x=［1，-1］

将初始系统状态设为x=［1，-1］，进行仿真实验，在仿真过程中，系统状态变量x（t）随时间的变化曲线如图8（a）所示，控制变量u（t）随时间的变化曲线如图8（b）所示。仿真实验表明，系统的状态变量在短暂波动后迅速收敛到目标设定值，利用本文所提方法可以快速实现式（26）二阶自抗扰控制的解耦问题。仿真图像表明，状态变量和控制变量都可以快速收敛，从而证明了本文方法的有效性和可行性。

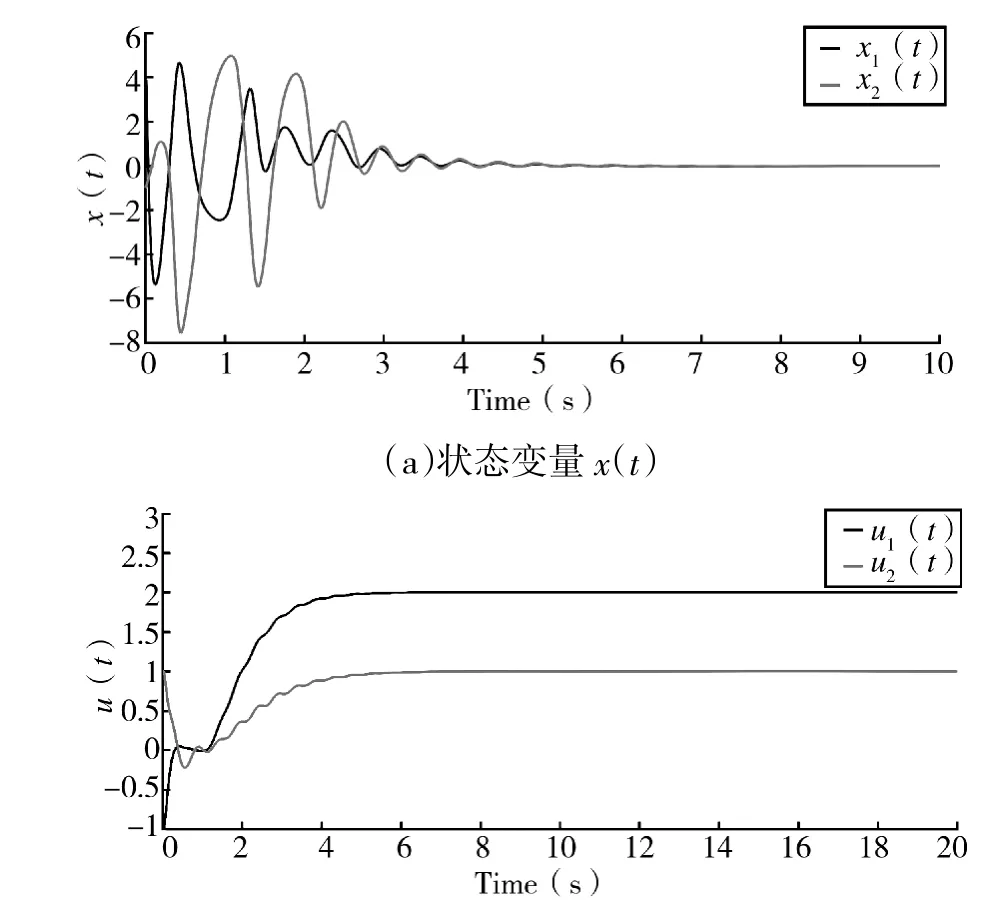
图8 系统初始状态为［1，-1］收敛曲线

3）初始系统状态设为x=［0.5，0.5］

将初始系统状态设为x=［0.5，0.5］，进行仿真实验，在仿真过程中，系统状态变量x（t）随时间的变化曲线如图9（a）所示，控制变量u（t）随时间的变化曲线如图9（b）所示。仿真实验表明，系统的状态变量在短暂波动后迅速收敛到目标设定值，利用本文所提方法可以快速实现式（26）二阶自抗扰控制的解耦问题。仿真图像表明，状态变量和控制变量都可以快速收敛，从而证明了本文方法的有效性和可行性。

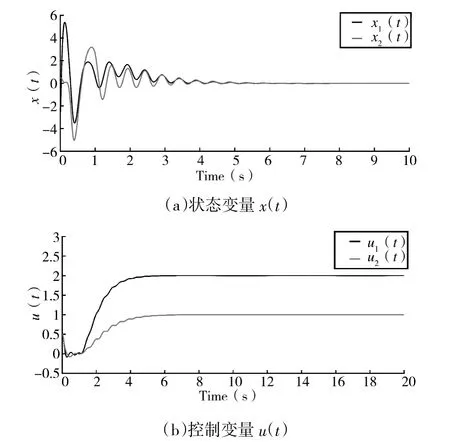
图9 系统初始状态为［0.5，0.5］收敛曲线

4 结论

本文首先分析了非线性多输入多输出自抗扰解耦控制中的求解逆矩阵问题。然后，将该问题概括为二阶、三阶、非方形和测量时变信号或高阶矩阵的求逆问题，并逐一给出相应的求解方法。对于时变测量信号或高阶矩阵，本文提出了一种基于高斯消元过程的LU 矩阵分解求逆方法，可以实时求解其逆矩阵。本文以二输入二输出非线性耦合系统为例，验证了所提求解逆矩阵方法及其在解耦ADRC 控制中的有效性和可行性。仿真结果表明，采用该求逆矩阵方法和解耦的ADRC 控制器信号，可以快速收敛到控制系统所设定的目标值。

该方法具有许多特点，首先，该方法非常适合于求解时变测量信号矩阵或高阶矩阵的逆矩阵，矩阵阶数越高，这种方法的优点就越明显。其次，这是对求解逆矩阵的一种动态求解方法，特别是对变系数矩阵的求解。第3，该方法由于避免大量中间数据的计算，大大缩短了计算时间。总之，这是一种实时的在线求逆方法，并具有较为充分的数学理论支撑。值得注意的是，这种方法是一种很有前景的新方法，因为它是一种在线数据驱动的动态求逆方法。由于该方法具有较为充分的数学理论支撑，为进一步研究非线性解耦ADRC 控制提供了新的研究思路，该方法将有助于完善非线性MIMO 解耦ADRC 控制的理论和方法。然而，本文提出的方法并不能解决所有不可逆奇异矩阵问题。因此，为使该方法更广泛地得到应用，需要进一步研究所提出的分解方法来解决逆矩阵问题。