尝试自己得出结论 促进数学核心素养提升

廖蓓蓓

【摘   要】“会用数学的思维思考现实世界”是数学素养的具体表现之一。学生经历自己得出结论的过程，有助于锻炼分析与解决问题的能力，发展数学思维。以“积的变化规律”一课为例，教师通过“巧用素材、质疑解析、应用模型、方法迁移”等方式，引导学生经历自己得出结论的过程，做到“言之有物、言之有据、言之有理、言之有瞻”。此外，教师结合教学实践提出“给足学生参与的时空，允许学生有试错的机会，提供人人有话说的素材”的思考，让数学素养的培育落到实处。

【关键词】积的变化规律;数学思考;解决问题;自己得出结论

“会用数学的思维思考现实世界”是数学素养的具体表现之一。学生经历自己得出结论的过程，有助于锻炼分析与解决问题的能力，发展数学思维。然而在实际教学中，学生自己得出结论时常常偏离核心或过于直观浅白，很难深入完整地对结论进行提炼。笔者以“积的变化规律”为例，谈谈如何为学生创设合适的学习环境，创造机会让学生能参与自己得出结论的过程，提升自己得出结论的能力。

一、教学内容分析

人教版教材四年级上册有探索“积的变化规律”这一内容，其中包括探索因数与积的协变关系，要求学生概述关系或以文字记录规律等教学内容。

“积的变化规律”是学生后续学习商的变化规律、运算定律、比例基本性质等内容的重要基础，也是引导学生经历抽象概括全过程，培养学生合情推理能力的好材料。从培养学生“会用数学的思维思考现实世界”这一角度看，这一内容的学习价值不仅仅体现在掌握“规律”本身，更重要的是让学生经历“数学思考”的过程，提升思维能力。

二、教学过程介绍

（一）巧用素材，使之“言之有物”

在对教材中的素材进行梳理与调整的基础上开始教学，引导学生在分析问题时做到“言之有物”。

1.经历初步形成结论的过程

教师呈现研究问题：

请你完成下面两组计算，你发现了什么？把你发现的现象写出来。

6×2=（  ）      4×25=（  ）

6×20=（  ）    12×25=（  ）

6×200=（  ）   48×25=（  ）

布置任务：①你发现了什么结论？②你是怎么发现这个结论的？③你觉得你发现的结论对吗？怎么证明它是对的？

交流学习：小组交流后得出以下三个结论。

结论1：第一个因数不变，第二个因数乘10，积也乘10;第一个因数乘几，第二个因数不变，积也乘几。

结论2：第一个或第二个因数不变，其余因数是倍数关系，积也是倍数关系。

结论3：某一个因数乘几，另一个因数不变，积就乘几。

2.辨析结论是否正确

教师组织学生针对以上三个结论进行讨论。因为结论1体现了规律从特殊到一般化的过渡，具有典型性，所以下面的教学围绕此结论展开。

（1）素材1：“第一个因数不变，第二个因数乘10，积也乘10”这个结论对吗？

生：对的。在左边这组算式中，先看前面两个算式。第一个因数6保持不变，第二个因数从2变为20，也就是乘了10，积也从12变成120，也是乘10。

生：从第2个算式到第3个算式也是这样的。第一个因数不变，第二个因数乘了10，积也是乘10。

师梳理并板书（如图1）：我们先理一理是怎么发现这个规律的。6不变，20=2×10，那么6×20=6×2×10，也就是“6×2”的积12再乘10。

生：当20×10的时候，积就是（6×20）×10=120×10=1200。200也可以看作2×100，那么6×200=（6×2）×100=12×100=1200。

生：6都不变，一个因数乘10，积就乘10;一个因数乘100，积就乘100。

（2）素材2：“第一个因数乘几，第二个因数不变，积也乘几”这个结论对吗？

生：对的。可以看右边这组算式中的前两个算式。算式中的第一个因数25一直保持不变，第二个因数从4变为12，因为4×3=12，所以12×25=（4×25）×3=100×3=300。

生：看第二组中的第1个算式和第3个算式，也有这样的规律。4×12=48，那么48×25=（4×12）×25=（4×25）×12=100×12=1200。

生：這句话在左边这组算式中也适用。

（3）比较结论优劣，理解结论的一般化。

教师引导学生对比前文中总结出的结论，对比“第一个因数不变，第二个因数乘10，积也乘10”和“第一个因数乘几，第二个因数不变，积也乘几”这两句话，思考哪句话的表达更清晰、更准确。

生：后面的好。第一句只讲一种情况，后面是用一句话概括所有的情况。

师：包括哪些情况？

生：一个因数不变，另一个因数乘10，积就乘10;另一个因数乘100，积就乘100;因数乘3，积就乘3;因数乘9，积就乘9。

师：还有其他情况吗？

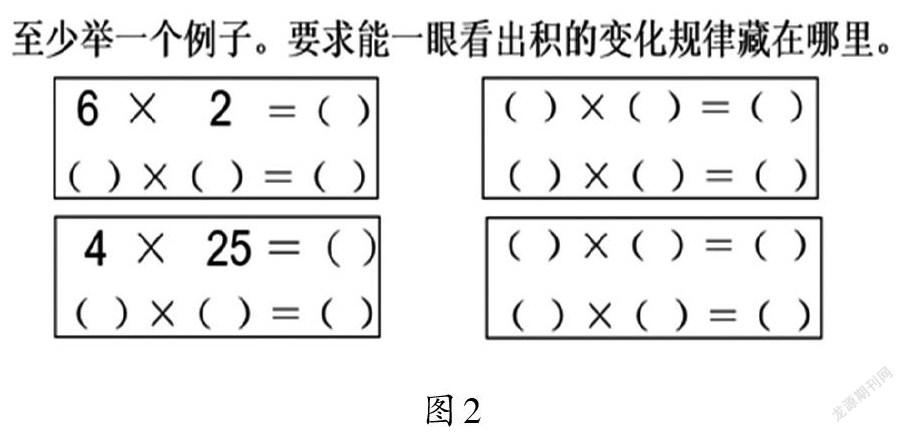
教师引导学生分两个层次举例，并记录（如图2）。

……

（4）对比归纳，修正结论。

师：结论2与结论3，所表述的意思一样吗？

生：我们组说的倍数关系，和乘几是同样的意思。

师：（指板书）关于“几”与“几”的关系，有具体要求吗？

生：积要跟着乘相同的数。

修正结论：一个因数不变，另一个因数乘几，积也乘相同的数。

以上过程，教师通过素材的呈现，引导学生观察、比较，不断发现、分析，理解规律蕴含的结构化思想，懂得提炼结论要“言之有物”。用“结论是否正确”来引导学生从结论倒回去看算式，通过对6×2与6×20，6×200积的变化规律的对比分析，清楚积的变化规律藏在两个算式的对比之中。再通过提问“哪个结论比较好”，引导学生对比结论的不同表述方式，经历从用具体数据描述规律到用“几”这样的一般性词汇描述规律的过渡。在这一过程中，学生更好地体会到结论一般化的含义，提炼了规律结构化的数学思想。

（二）质疑解析，使之“言之有据”

结论的得出必须要有依据，有依据的结论才具有科学性。教师应首先引导学生对结论的一般性进行质疑，解释结论的表述是否完整，让学生体会“推理的严密性”，再引导学生用学过的知识，如面积模型、乘法的意义等对结论的合理性进行解释，体现“言之有据”。

1.分析结论的合理性

（1）质疑。

师：我们举了这些例子后，是不是就可以说明结论一定合理？

生：还要举更多的例子，例子是举不完的。

师：如果能找到它的反例，就可以说明结论不成立。

生：0除外。

师：这是对数的要求做补充。（板书：0除外）

（2）解释。

师：如果找不到反例，那么我们说暂时这个结论可用。除此之外，你还有什么办法能解释此结论确实合理吗？

生画图解析：我画了一个长方形，长是5，宽是4。如果长不变，宽乘2，面积就乘2。如果宽不变，长乘2，面积也是乘2。

……

借图归纳：长方形面积用“长×宽”来表示，在长与宽中，一个数不变时，不管是长乘几或者宽乘几，面积都会跟着乘相同的数。这和积的变化规律完全一致。

（3）总结。

看来，通过面积图或者对乘法意义的解释，确实可以说明以上总结出的“积的变化规律”是存在的。

2.完善“积的变化规律”

师：研究到这儿，你还能“推”出其他的猜测吗？

生：如果一个因数不变，另一个因数除以几，或者加上几、减去几，积是不是也会随着发生同样的变化？

学生提出猜测后，教师引导学生推翻不成立的猜测，解释成立的猜测，并用一句话把规律写完整。

（三）应用模型，使之“言之有理”

模型建立后，应用模型的过程既是对模型进行巩固的过程，也是从归纳走向演绎，用已经证明是正确的规律解决问题的过程。在这个过程中，学生要做到“言之有理”。

教师出示问题：

（1）如果A×8=200，那么A×8×3=？

（2）如果A×8=25，那么A×8×3=？A×32=？

学生解答问题……

教师呈现学生解决问题（1）的两种情况。

情况1：A=200÷8=25，A×8×3=25×8×3=200×3=600。

情况2：A×8×3=200×3=600。

教师追问：情况2中的200是从哪里来的？

生：因为A×8=200，所以可以用200代替“A×8”。

师：用这两种方法都能得到答案，给两种方法各取一个名字，你会怎么取？

生：第1种叫按步计算法，第2种叫打包法。

……

师：看问题（2），如果A×8=25，要求A×8×3=？你选哪种方法？

生：用打包法。因为这道题要把A求出来，那是有小数的，不好算。

生：用打包法更方便，A×8就是25呀！25×3=75，一下子就算出来了。

师小结：看来可以把“A×8”看成一个标准，快速求出“A×8×3”的积。

教师再次出示题目：A×32=？请学生计算并写出思考过程。

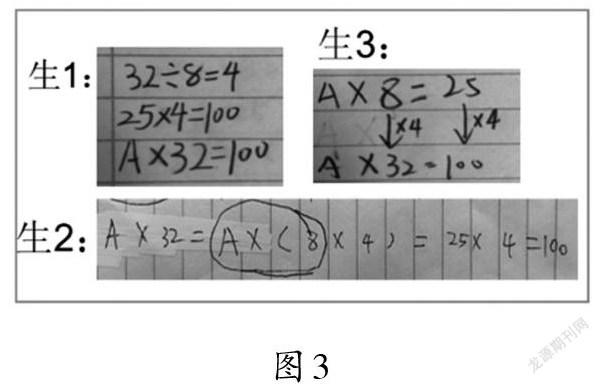
学生解题后，教师呈现学生作品（如图3）。

教师引导学生思考并交流：①三种方法有什么相同的地方？②生2作品中的（8×4）是什么意思？“A×8”圈起来又是什么意思？③根据A×8=25，你还能求哪些算式的积，看谁想得多……

“打包法”以“A×8”的积为参照标准，可求出“A×8×3”与“A×32”的积。学生在解决问题的过程中体会“A×8”与“A×32”的关系。图中生2的方法是将规律作为一个结论使用，这其实就是对后续要学习的乘法结合律的实际应用。学生自主编题求积，是结构化模型的再应用，对促进自身数学思维的发展具有重要的意义。

（四）方法迁移，使之“言之有瞻”

在本课学习之后，学生获得了探索规律的一般方法和经验，这为他们后续的探索和研究提供了学习路径，使之“言之有瞻”。

1.回顾梳理

师：这堂课我们分几个步骤研究了积的变化规律？

2.追问

师：研究积的变化规律后，你还想研究什么？

借问题给学生提供研究方向：①两个因数同时变化时，积会怎么变？②两个因数发生怎样的变化，积不变？引导学生选一个问题课后进行探究。

学生由本节课研究的“积的变化规律”联想到“如果两个因数同时变化，积会怎么变”以及根据“积的不变规律”联想到“商的变或不变规律”等。本课探索规律的研究路径，为学生后续的规律探索提供了方法上的支持。这些活动经验与数学思考将支持学生的长久发展。

三、教学实践启示

選择合适的素材，创设有价值的活动，让学生经历自主得出结论的过程，可以培养学生的数学思维，促进其核心素养的提升。要达到此目的，教学时，教师需要做好以下三件事情。

（一）给足学生参与的时空

学生要自己得出有价值的结论，需要经过积极深入的思考和钻研，经历观察、发现、分析、归纳等学习过程。因此要给学生提供充足的时间，并为学生提供独立思考的机会，让他们先尝试记录想法，再与同伴充分地讨论、交流，经过比较、辨析，让大多数学生都能完整经历过程，深入思考结论。

（二）允许学生有试错的机会

数学学习是知识不断扩充、能力不断发展的过程，纠错也是数学学习的必要途径。教师应允许学生有试错的机会，可以经常使用“写下你发现的结论”这样的方式让学生尝试有深度的思考。同时，教师不要立即对学生的结论给出评价，而要通过学生间的交流、讨论，让他们尝试自己发现问题，从而得出正确的结论。

（三）提供人人有话说的素材

教师在挑选教学素材时，需考虑学生的不同水平层次，设计让人人都有话说的素材。如本课中“已知A×8=200，求A×8×3=？”学生都能求解，但解题方法未必相同;“A×8=25，A×32=？”学生得到的答案是相同的，但他们记录的思考过程及方式却不一定相同。这些都是让人人有话说的好素材。

参考文献：

[1]李光树.小学数学学习论[M].北京：人民教育出版社，2014：167-203.

[2]程靖，孙婷，鲍建生.我国八年级学生数学推理论证能力的调查研究 [J].课程·教材·教法，2016（4）：17-22.

[3]林碧珍.数学臆测引发数学论证的课堂实践（上）[J].小学教学（数学版），2018（4）：4-7.

（浙江省温州市永嘉县瓯北中心小学   325102）