质量守恒润滑模型的快速数值计算方法*

顾春兴 戴 黎

(上海理工大学机械工程学院 上海 200093)

在大多数机械系统中，流体动压润滑是广泛存在的。这些机械系统包括径向滑动轴承系统、止推轴承系统、活塞环/缸套系统和机械密封系统等。一般情况下，当机械系统的2个接触面之间存在收敛和发散间隙时，2个接触面间将会产生流体动压力。此时，润滑油能有效地分离接触表面以减少摩擦[1]。

近年来，表面织构作为一种降低摩擦磨损的有效手段，在学术界和工业界得到了广泛的应用和研究[2-7]。然而，在涉及流体动压润滑的数值模拟中，流体润滑区域可能会出现空穴现象[8-10]。同时，由于表面织构的存在，润滑油膜破裂后会发生润滑油膜的重构。因此，在计算流体压力时，需要对空穴边界进行质量守恒处理，以准确地完成摩擦学系统润滑性能的预测[11]。在过去的几十年里，人们提出了不同的质量守恒空化算法。其中，由JAKOBSSON和FLOBERG[12]、OLSSON[13]提出的JFO(Jacobsson-Floberg-Olsson)空化边界条件具有特殊的地位，已经在很多研究中得到了成功应用。

然而，采用质量守恒的空化边界条件将会使流体动压润滑模型的求解变得不稳定，计算时间增加。此外，润滑模型的求解时间还与网格密度有关。在表面织构的模拟中，常需要采用精密的网格才能精确地表征表面织构。网格数的增加将导致数值计算的时间成倍增加。因此，在求解含有质量守恒空化边界条件的雷诺方程时，高效和稳定的求解方法是迫切需要的。

为了解决由网格细化和采用质量守恒空化边界条件引起的润滑模型不易收敛和计算时间过长的问题，本文作者通过结合Fischer-Burmister-Newton-Schur (FBNS)方法和网格细化(GR)策略，提出一种高效的数值计算方法。采用这种数值计算方法将显著减少流体动压润滑模型的求解时间。

1 数学模型

1.1 控制方程

为了预测油膜压力，文中将采用具有JFO空化边界条件的二维雷诺方程[12-13]。方程式如下：

(1)

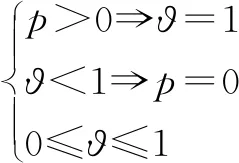
(2)

式中：p为油膜压力；h为油膜厚度；ϑ为流体饱和度；ρ为润滑油密度；μ为润滑油黏度；t为时间步长。

流体饱和度ϑ和油膜压力p之间的关系可由公式(2)揭示。如公式(2)所示，当油膜压力p大于空化压力(pca=0)时，ϑ设为1。当油膜压力p等于空化压力时，流体饱和度ϑ将小于1。

1.2 加速收敛的数值计算方法

在含油润滑机械系统的数值模拟中，求解流体润滑模型往往需要多次迭代。因此，流体润滑模型的求解速度是非常关键的。数值模拟的运行时间取决于流体润滑模型的收敛速度。因此，迫切需要加快流体润滑模型计算速度的方法。

文中所提出的高效的数值计算方法，采用如下2种方法，以提高流体润滑模型的计算效率。一方面，计算中将采用FBNS方法[14]，以提高流体润滑模型求解的稳定性和收敛性。FBNS方法的采用，可以将流体润滑模型(一个约束问题)的求解转化为一个无约束问题的求解，而无约束问题的求解则可以直接采用现有的商用求解器。文献[14-15]中已经给出了FBNS方法的详细步骤，文中不再详述，下面仅简要介绍FBNS方法的求解步骤。按照FBNS方法，首先需要对考虑JFO空化边界的雷诺方程进行修改[12-13]。质量守恒的空穴边界条件将采用一个互补约束来代替。相应的表达式如下：

(3)

(4)

其中θ=1-ϑ。当且仅当p、θ≥0和pθ=0时，公式(4)所涉及的约束条件才能满足。根据文献[14]可知，采用FBNS方法求解流体润滑模型，其计算速度将明显快于传统方法(2个数量级)。

如图1所示，沿x和y方向对研究对象进行网格划分。网格点沿x方向的位置用i进行标记，沿y方向的位置用j进行标记。网格点(i,j)处的油膜压力可以用p(i,j)表示，网格点(i,j)处的油膜厚度可以用h(i,j)表示。流体润滑模型数值方程可采用有限体积法进行离散。如图1所示，分别使用下标P、E、W、N、S、e、w、n和s来替换下标(i,j)、(i+1,j)、(i-1,j)、(i,j+1)、(i,j-1)、(i+0.5,j)、(i-0.5,j)、(i,j+0.5)和(i,j-0.5)。

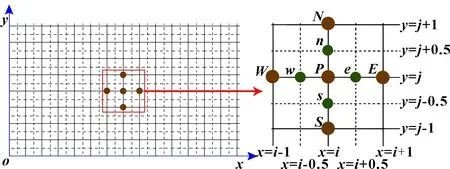
图1 流体动压润滑模拟中的网格点分布情况

基于有限体积法，公式(3)可以分解成[15]：

6ΔyU[(1-θW)ρWhW-(1-θP)ρPhP]+

(5)

其中he=0.5(hE+hP),hw=0.5(hW+hP),hn=0.5(hN+hP),hs=0.5(hS+hP),ρe=0.5(ρE+ρP),ρw=0.5(ρW+ρP),ρn=0.5(ρN+ρP),ρs=0.5(ρS+ρP),μe=0.5(μE+μP),μw=0.5(μW+μP),μn=0.5(μN+μP),μs=0.5(μS+μP)。另外，带上标pre的项代表前一时间步的项,Δt则表示时间步长。

因此，对公式(5)进行重新排列，可得如下表达式：

ANPN+ASPS+APPP+AWPW+AEPE+BPθP+BWθW+CP=0

(6)

公式(6)揭示了油膜压力和流体饱和度之间的线性关系，因此离散化结果可以表示为

G(p,θ)=Ap+Bθ+c=0

(7)

式中：A是包含AN、As、AP、AE和AW的信息的矩阵；矩阵B包含BW和BP的信息；c是包含边界条件和CP信息的向量。

此外，公式(4)可离散为如下的表达式：

(8)

公式(8)所示的离散化结果可用如下表达式表示：

(9)

另一方面，如图2所示，可采用GR(网格细化)策略以进一步加快流体润滑模型的计算速度。在GR策略中，粗网格上的p和θ的最终解将作为细网格上p和θ的初始值。通过这种方式，可保证细网格上p和θ的初始值接近于最终解。根据牛顿迭代法的特点，当初始值足够接近最终解时，牛顿迭代法具有二次收敛。另外，由于网格数目较少，粗网格上数值计算的收敛速度相对较快。当合理选择网格层数时，GR策略可以有效地缩短计算时间。

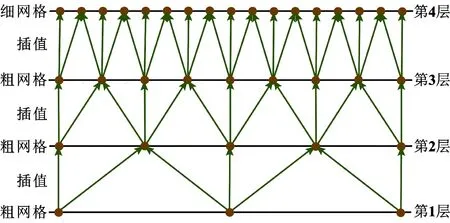
图2 网格细化策略示意

在GR策略中，较低网格层(亦称粗网格)上的计算结果应该首先进行插值，然后才能用作较高网络层(细网格)上的计算初始值。基于流体润滑压力和流体饱和度的特点，文中所采用插值算法为非线性插值运算，相应的表达式为

uk(i,j)=uk-1(I,J),i=2I,j=2J

(10)

9uk-1(I+1,J)-uk-1(I+2,J)),i=2I+1,j=2J

(11)

9uk-1(I,J+1)-uk-1(I,J+2)),i=2I,j=2J+1

(12)

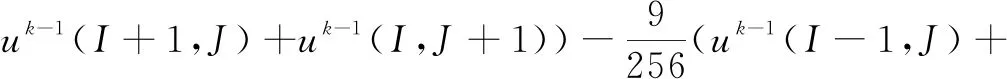
她的高烧退了一些，但仍然烫着，青辰继续给她煎药，喂药，喂米汤或者面汤，然后再给她擦洗四肢，一套忙活下来，大半天的时间便已过去。

uk-1(I,J-1)+uk-1(I,J+2)+uk-1(I+1,J-1)+

(13)

其中uk(i,j)是第k网格层中的参数，而uk-1(I,J)位于第k-1网格层中。

图3总结了流体润滑模型的快速数值计算流程，其中Gr为所采用的网格层数。在每一网格层的计算中，p和θ值需要不断更新，直到更新的值(在当前迭代步)和前面的值(在前面的迭代步)之间的偏差小于或者等于一个允许的精度(10-6)。

图3 流体润滑模型的快速数值计算流程

2 结果和讨论

2.1 油膜厚度的表征

油膜厚度的表征是流体润滑数值计算的关键。摩擦学系统中油膜厚度是最小油膜厚度和轮廓形状之和。其表达式如下：

h(x,y)=h0+hprof(x,y)

(14)

式中：hprof(x,y)是轮廓形状。

织构化的表面轮廓的表达式[16]如下:

(15)

式中：Λ=|x′cosα±y′sinα|cosα[16]；α代表凹槽角度；dg是平均凹槽深度；wg表示平均凹槽宽度；x′和y′都在局部坐标轴上，而局部坐标位于织构单元的中心。

图4给出了织构化轮廓的数值重建云图。其中，量纲一X可由X=(2x-b)/b，而量纲一Y可由Y=(2y-l)/l计算，b表示接触面的宽度，l表示接触面的长度。

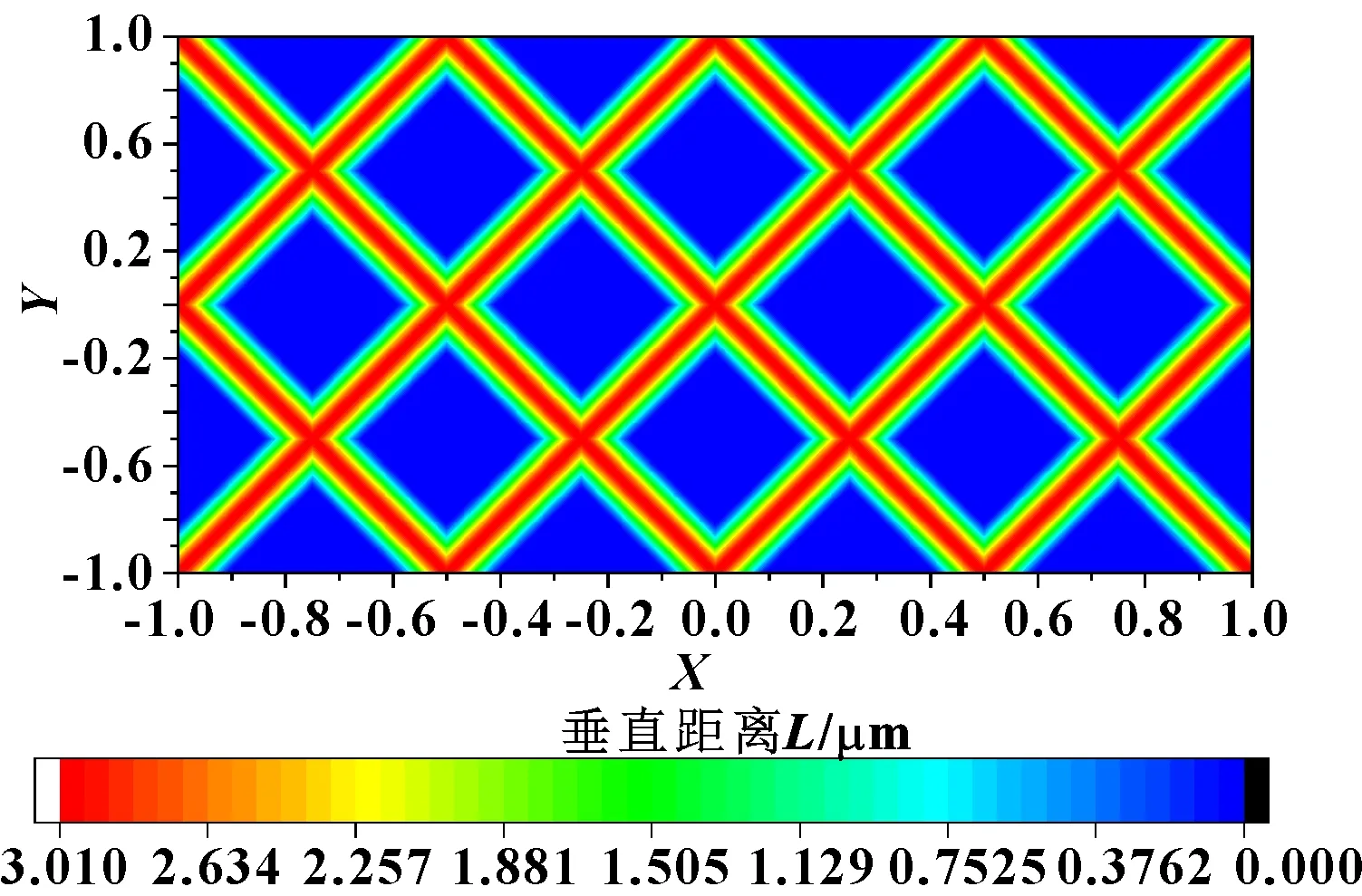
图4 织构轮廓的数值重建云图

2.2 数值模拟条件

为了评估所提出的快速数值计算方法的有效性，进行了一系列稳态仿真试验。在这些算例中，假定滑动速度为10 m/s，润滑油黏度为0.004 Pa·s，润滑油密度为860 kg/m3。同时，织构轮廓尺寸如下：沟槽深度为3 μm，沟槽宽度为40 μm，凹槽角度设为45°。织构单元尺寸为200 μm×200 μm，接触面长度为800 μm，接触面宽度为400 μm。文中对3种算例进行数值计算，以评估所提出的快速数值计算方法的求解效率。3种算例所采用的最小油膜厚度分别为0.141、0.283和0.566 μm。即，3种算例的最小油膜厚度值分别为综合表面粗糙度的0.5倍、1倍和2倍。数值模拟条件见表1中。

表1 数值模拟条件

2.3 网格收敛性研究

在评估所提出的快速数值计算方法的计算效率之前，首先应该进行网格收敛性研究，以评价网格数量对数值计算结果的影响。在流体动压润滑模拟中，网格必须足够精密，才能精确地表征表面轮廓。如图5所示，当网格大于1 200×600时，最大流体压力的计算结果将趋于稳定，逐渐接近于精确值。因此，在下面的数值计算中，将采用1 200×600网格。

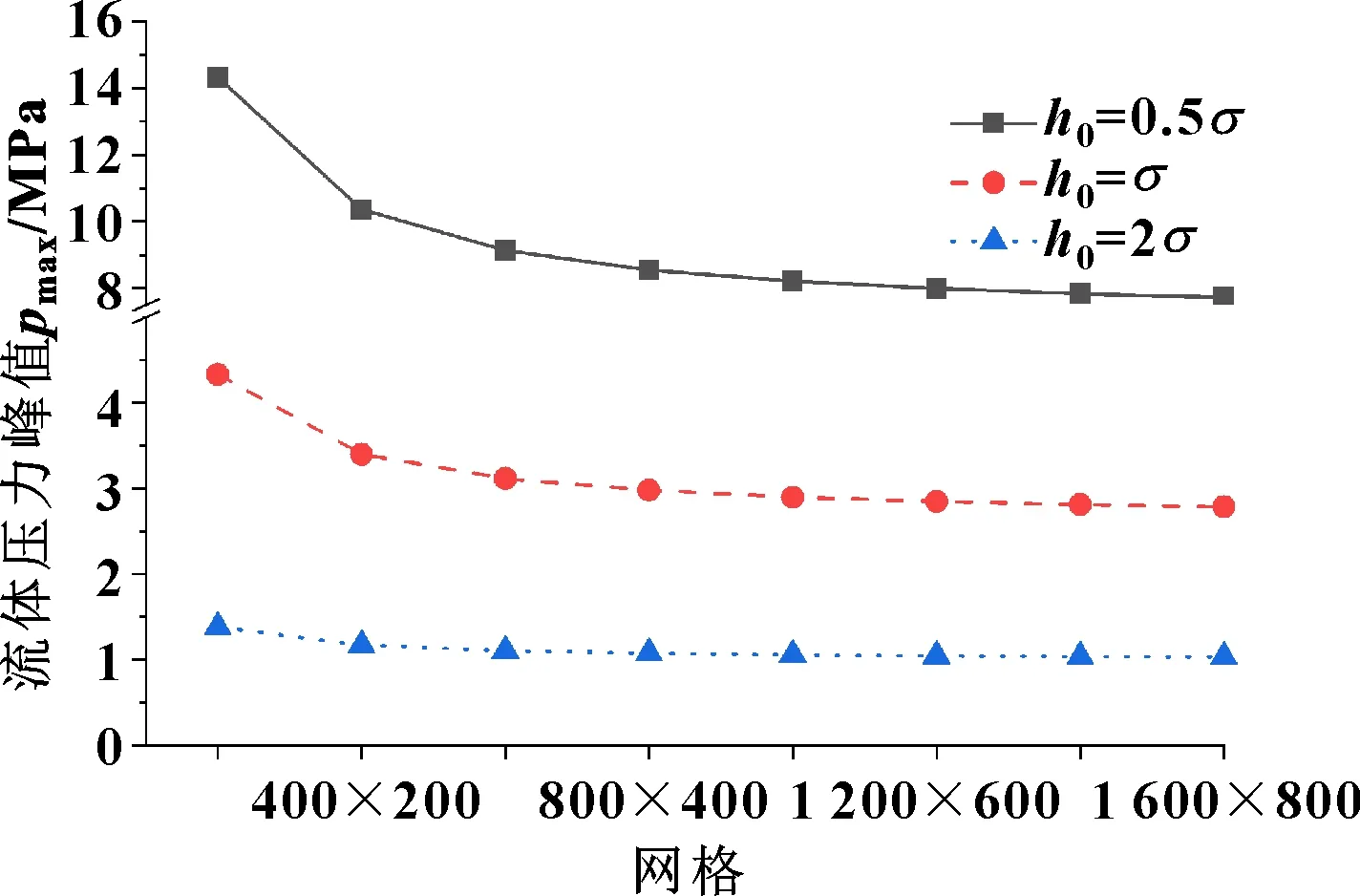
图5 采用不同网格时的最大流体压力的计算结果

2.4 标准方法和改进方法结果比较

针对3种算例，采用标准方法和文中所提出的快速数值计算方法进行计算。在标准方法中，将采用FBNS方法来计算流体压力。在快速数值计算方法中，将结合FBNS方法和GR策略来加速流体压力和流体饱和度的计算。同时，还将分析网格层数对计算速度的影响。根据前文针对网格收敛问题的分析，以下模拟将采用1 200×600网格。数值计算是在一台配备英特尔酷睿i7-7700 CPU的计算机(每个核心的时钟频率为3.60 GHz，内存为24 GB)上进行的。

图6显示了3种算例的流体压力分布情况。需要指出，标准方法和快速数值计算方法所预测的流体压力结果是完全一致的。这是因为：如图3所示，标准方法和快速数值计算方法的主要差异在于是否采用GR策略。在快速数值计算方法中增加了GR策略，按照GR策略，为了使牛顿迭代法具有二次收敛，细网格(目标网格)上的p和θ初始值是由粗网格上p和θ的最终解通过插值获得的。然而，无论是标准方法还是改进方法，p和θ最终解的计算总是在细网格上进行的。因此，这2种方法所求的结果是完全一致的，其主要差异在于求解效率。

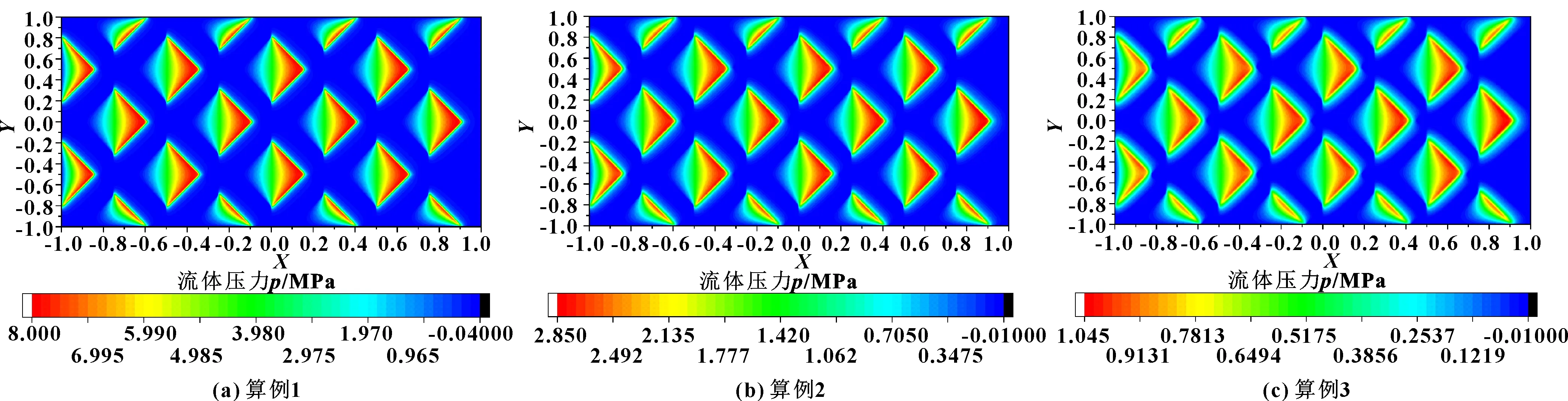
图6 3种算例的流体压力分布

图7示出了3种算例采用不同方法进行求解所需的计算时间。计算时间是通过CPU时间衡量的，可以发现，与标准方法相比，考虑多层网格的快速数值计算方法可以显著减少计算时间。当采用快速数值计算方法时，每个非目标网格层的计算都将有助于目标网格层上的精确初始值的获取。研究结果表明，对于不同的算例，与传统方法相比，快速数值计算方法可缩短73%～81%的数值计算时间。在快速数值计算方法中，由于初始值更加接近精确值，目标网格上的计算能够迅速收敛。事实上，在一个完整的计算流程中，流体压力分布的更新需要进行多次，即需要多次求解流体润滑模型。因此，加快求解流体动压润滑模型，就能显著减少整个计算流程的时间。可见，采用快速数值计算方法来求解流体润滑模型可明显提高求解效率。

图7 3种算例采用不同方法所需的计算时间

3 结论

(1)提出一种高效精确的面向流体润滑模型的快速数值计算方法，该方法结合了Fischer-Burmsister-Newton-Schur(FBNS)方法和网格细化(GR)策略，可以高效地求解流体润滑模型。

(2)采用传统数值方法和快速数值计算方法求解不同算例，结果表明，采用快速数值计算方法得到的流体压力与传统方法得到的结果完全一致；同时，采用快速数值计算方法能够有效减少计算时间，计算时间下降可达73%～81%。在一个完整的计算流程中，会执行多次润滑模型的求解。因此，采用所提出的快速数值计算方法，将能大大减少整个计算流程的计算时间。