昔格达土的压缩特性和微观结构

卢志鹏,孔玉侠,2,王慧娟,汤洪文

(1.南京工业大学 交通运输工程学院,江苏 南京 210009; 2.南京工业大学 岩土工程研究所,江苏 南京 210009)

昔格达地层成分复杂,由杂色的黏土岩及粉细砂岩组成,主要覆盖于早第三系地质类型之上,分布于我国西南山区河谷及山间宽谷地带,是韵律互层的静水河湖相沉积型土,在不同地区,其物理力学性质差异很大[1]。昔格达土具有似土非土、似岩非岩的外在特征,水稳性较差,因而具有易滑、易发生地质灾害等工程地质特点。何能方等[2]对攀枝花西侧特有的昔格达黏土岩的结构成因进行了分析,表明昔格达黏土岩在天然状态下具有较强的结构特性。郭伟杰等[3]研究含水率对压缩性能的影响,发现在前期固结应力作用下,含水率对压缩系数的影响较大,且含水率越高,压缩系数变化越大。在此基础上,王立忠等[4]对昔格达土的压缩性能进行了研究,发现不同的加载速率对原状土压缩系数的影响较大。而陈晓平等[5]发现结构性土的压缩曲线一般分为3段:初始平缓段、陡降段、与重塑土平行段。罗庆姿等[6]取不同深度的海相原状软土进行一维压缩试验和蠕变试验,在压缩试验中发现初始压缩系数与土的天然含水率、孔隙比之间具有良好的线性关系。

土体微观结构研究始于20世纪中期,随着电子科技的引入以及新的数学方法的出现,使得微观结构的研究取得重大飞跃。国内对土体微观结构的研究起步较晚,关于昔格达土微观结构的研究更少。Osipov等[7]认为天然黏土的微观结构主要有7种类型,分别为蜂窝状、质基状、絮状、层状、畴状、假球状和海绵状,这一观点逐渐成为学术界的主流观点。胡瑞林[8]最早在国内提出了微观结构特征的分类问题,认为可分为孔隙的变化特征、土颗粒的联结特征及颗粒排列特征。蒋明镜等[9]基于三轴压缩试验,利用扫描电子显微镜(SEM)和定量分析技术,讨论结构性黏土剪切带的内外微观结构特征。王宝军等[10]利用图像处理技术对黏土样进行微观结构分析,建立了分形维数和微观结构之间的关系。刘雪梅等[11]结合图形处理技术和沙盒(sandbox)分形理论,研究黏土的微观孔隙变化及其分形特征,探讨二值化分割阈值对孔隙划分的影响。张季如等[12]利用专业图像分析软件IPP,对黏土的孔隙分形维数进行测算,并利用IPP软件的图像采集、处理、尺寸测量、计数等功能,得出黏土的孔隙结构具有明显的分形特性,揭示了分形维数与黏土的力学参数、微观结构参数之间的关系[13]。

目前国内外的学者对昔格达土的成因以及防灾减灾工程有较多的研究,Ahmed[14]研究了青藏高原的隆升与昔格达地层形成的关系。周平等[15]从力学变形本构模型的角度对昔格达地层隧道围岩变形机制进行了分析。成永刚等[16]主要进行了昔格达地层填方路堤滑坡原因的分析,并提出了防治措施。但是对昔格达土的结构压缩特性以及微观结构研究较少,缺乏将昔格达土的宏观力学特性和微观结构特征相结合的比较研究。本文以攀枝花西侧的两处典型河湖相沉积型昔格达土为研究对象,根据原状样和重塑样的室内压缩试验结果及其微观结构,探讨昔格达原状土和重塑土的宏观力学特性及微观结构表达。

1 试验

1.1 样品获取

原状样取自河湖相天然沉积型昔格达土,采用两侧直径72 mm、高度60 mm的钢管薄壁取土器进行取样。两处原状样取土地点位于攀枝花西侧的建筑工地(图1),坐标分别为(N 26°31′24.0″,E 101°43′39.6″)和(N 26°30′52.9″,E 101°44′06.3″)。

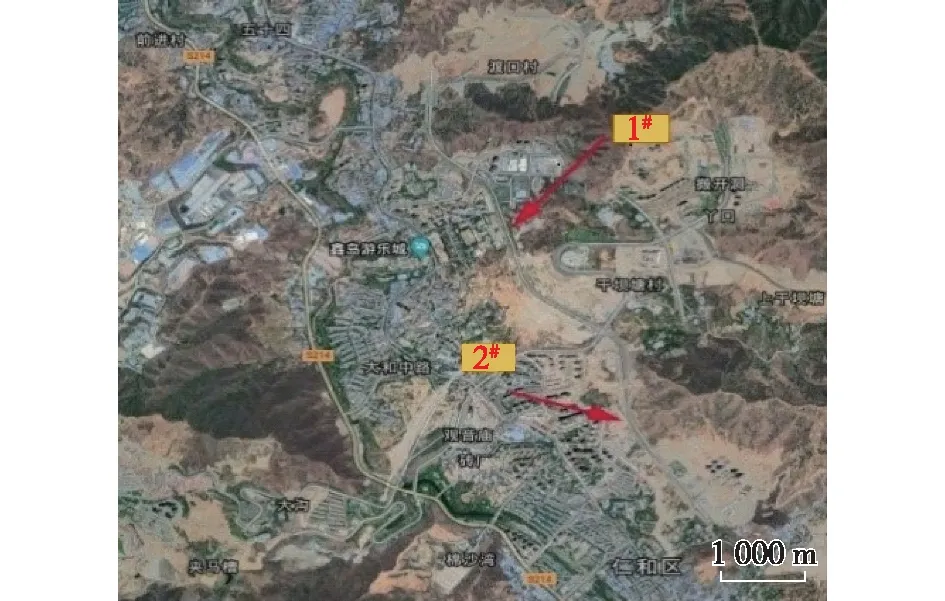
图1 采样位置图Fig.1 Sampling location map

使用高度2 cm、面积30 cm2的环刀对昔格达土进行制样,并按照土工规范要求进行室内土工试验,结果如表1所示。

表1 土工试验结果

昔格达岩土层在每一个地质单元内都存在空间粒度分布呈现为向上变细的韵律沉积特质,现将1#和2#昔格达土采用筛析法分析粒径范围为0.075～2 mm时的颗粒级配,取筛后的细粒土用密度计法测定其颗粒组成,图2为不同位置处的昔格达土颗粒级配分布曲线。

图2 两处昔格达土颗粒级配曲线Fig.2 Grading curves of two sites of Xigeda soil

由图2可知:粒径为0.005～0.075 mm的昔格达土含量居多,而黏粒组(<0.005 mm)的土含量较少。黏土中的黏粒含量对昔格达土的流变特性、压缩性能以及整体强度有着很大的影响。2#昔格达土的黏粒含量较1#昔格达土的多,由文献[17]可知:当黏粒发生水化后,实际会增加土体中固相的体积,减少土体内的自由水,使土体的黏度变大。

1.2 一维压缩试验方案

本试验为侧限压缩试验,试验设备主要采用WG-1C系列单杠杆三联固结仪,试样高度(h)为2 cm、直径(d)为6.18 cm。为了得到较为明显的结构特征,按照每24 h加载100 kPa,至最大1 200 kPa时为止。根据试样高度变化量(Δh),计算孔隙比(e)在不同阶段的变化规律,得到原状样和重塑样的压缩曲线。

1.3 SEM表征

首先，根据试样的扰动和加载情况分别制备相应的SEM样品,选择具有代表性的放大4 000倍图像作为分析对象,在选择图像时应注意图像面积要保持基本一致；然后，利用IPP图像处理软件对土样中土颗粒的周长、面积、轴长等微观结构特征进行定性描述;最后，利用软件测得的特征数据，计算得出微观结构参数,进行定量分析。

2 结果与分析

2.1 X线衍射

用X线衍射(XRD)分析方法对昔格达土矿物成分进行分析,结果如图3和表2所示。

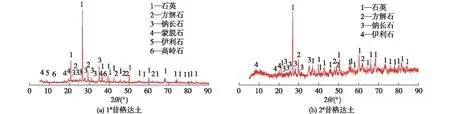
图3 X线衍射图谱Fig.3 X-ray diffraction patterns

根据“三峰法”对X线衍射图谱进行分析,由图3(a)可知：1#昔格达土主要矿物成分为石英和方解石。由图3(b)可知：2#昔格达土的主要矿物成分为石英、方解石和钠长石,但2#昔格达土缺少了蒙脱石和高岭石。由表2可知:昔格达土矿物成分中质量分数最多的是石英,方解石次之。

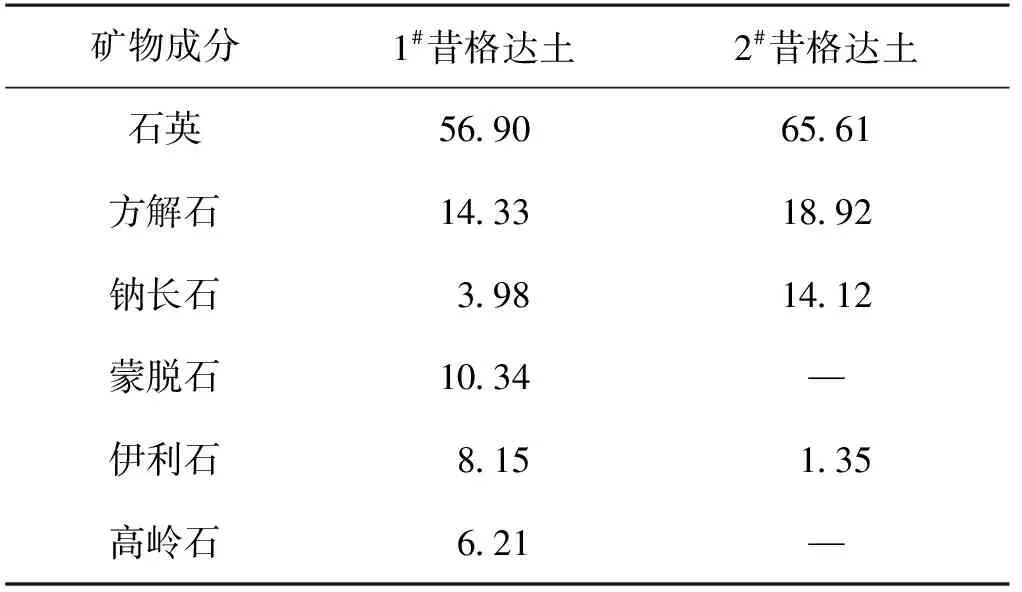
表2 矿物成分的质量分数(半定量)

2.2 一维压缩参数

2.2.1 压缩曲线

试验中共有48个土样,其中8个为原状样,其余为重塑样。重塑样的含水率(w)为5%、10%、15%、20%。孔隙比(e)与lgp(p为固结压力)的压缩曲线如图4所示。

由图4可知:1#原状样表现出了明显的结构特征,曲线前缓后陡,在500 kPa处出现拐点。重塑样在高固结压力处趋于重合,高含水率(w)的重塑样曲线一直在含水率较低的曲线上方。1#原状样与重塑样在高固结压力下呈现出重合趋势，2#原状样曲线没有明显的拐点,重塑样和原状样曲线在高固结压力下也没有表现出重合趋势。

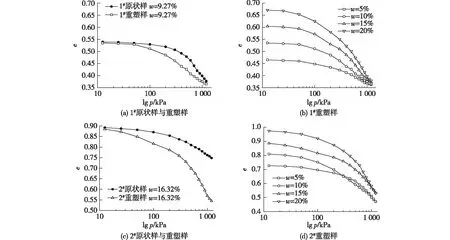
图4 昔格达土e-lg p曲线Fig.4 e-lg p curves of Xigeda soil

2.2.2 压缩系数

图5为昔格达土原状样和重塑样的p-压缩系数(av)曲线,av均随着固结压力的增大而逐渐降低,2#昔格达土表现得更为明显。利用100～200 MPa范围内的压缩系数(av1-2)来评价土的压缩性能。1#原状样的av1-2为0.100,而2#原状样的压缩系数为0.166,因此1#昔格达原状土压缩性能要低于2#昔格达原状土压缩性能。

由图5(a)和5(b)可知:高含水率、高孔隙比的1#重塑样的压缩系数开始时较大,然后在固结压力作用下不同含水率的重塑样压缩系数均迅速变小并趋于一致。而图5(d)中的2#昔格达土压缩系数却并未表现出趋同性。在相同固结压力下,随着含水率的增大,压缩系数随之增大,含水率能够显著影响昔格达土的压缩特性。由图5(c)可知:2#昔格达土由于取土深度相对较浅,受到的先期固结压力小,密实度小,所以孔隙比较大,因此在压缩初期压缩系数下降较快,具有高压缩性。

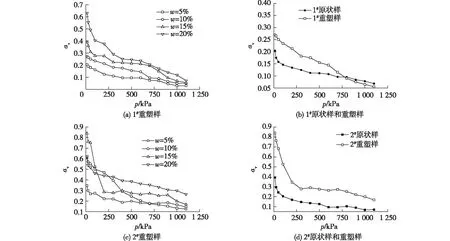
图5 昔格达土p-av曲线Fig.5 p-av curves of Xigeda soil

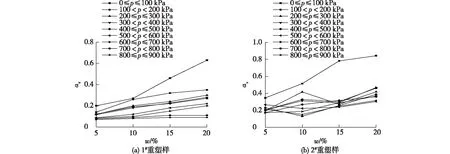
图6 昔格达土重塑样的av-w曲线Fig.6 av-w curves of remolding Xigeda soils

图6为昔格达土重塑样的av-w曲线。由图6可知:在相同的压力段下,昔格达土的压缩系数随着含水率的增大而增大,在0≤p≤100 kPa范围内的变化尤为明显;当p≥600 kPa后,压缩系数不再随着含水率的变化发生明显变化。

2.2.3 综合结构参数

土的结构性强弱往往不是由单一参数如压缩系数、压缩指数等决定,而是由多个参数共同作用的结果。因此，谢定义等[18]根据土力学的办法,首次提出了一个全面反映土体结构性强弱的指标,即综合结构势:在某一竖向压力下以昔格达原状、重塑和饱和土的孔隙比为变量的结构参数,如式(1)和(2)所示。

m1=es/ey

(1)

m2=ey/er

(2)

式中:ey、es、er分别为昔格达原状、重塑和饱和土的孔隙比。

m1越大表示结构可变性越强，m2越小表示结构可稳性越强。将m1和m2结合起来,将综合结构参数(mp)定义为

(3)

土的联结特性越强、排列特性越弱,在加荷、扰动和浸水的情况下,土的孔隙比越小,即mp越大。

图7为不同含水率下1#昔格达土的综合结构参数曲线。由图7可知:当固结压力大于1#昔格达土的结构强度,并在一个较小的范围内时,综合结构参数处于极不稳定状态,在100～500 kPa范围内即产生较大变形;而当固结压力进一步增大至800 kPa以上时,土体处于一个稳定状态，再难被压缩。

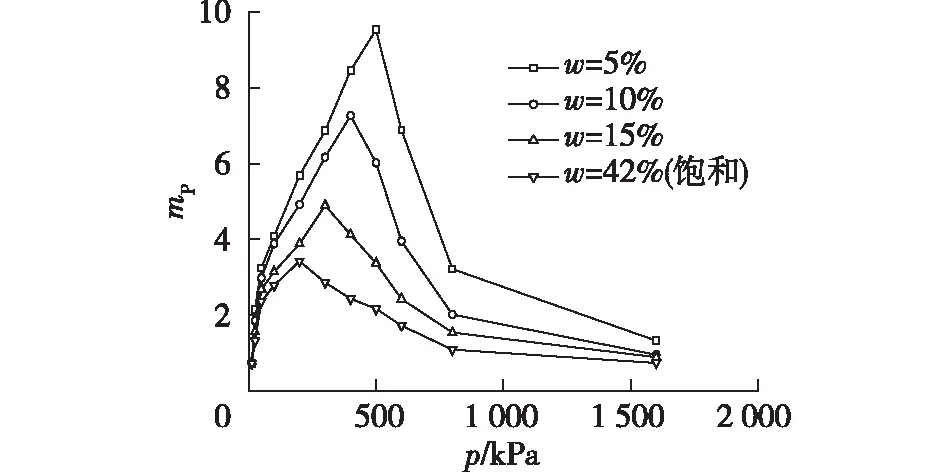
图7 不同含水率下1#昔格达土综合结构参数曲线Fig.7 Composite structural parameter curves of the 1# Xigeda soil under different water contents

2.3 微观结构定性分析

采用液氮真空冷冻升华干燥法制备样品,昔格达土原状样以及重塑样的扫描电子显微镜(SEM)照片如图8所示。

由图8(a)和8(b)可知：未压缩1#原状样的基本单元体呈开放式絮凝片状结构,颗粒分布有一定方向性,土体中扁平的黏土矿物组成聚合体；未压缩2#原状样孔隙相对较小,且片状黏粒相互凝聚交叠、大小均匀、排列相对紧密,构成黏粒聚合体。图8(c)为未压缩1#重塑样,也是片状结构,但出现明显的黏土集粒,孔隙相对较小,呈点状、线状和镶嵌状接触。图8(d)为未压缩2#重塑样,相对于原状样更加致密,黏粒附着在团聚颗粒上,土颗粒间的链接被打断,聚粒型颗粒遭到破坏,转变成许多小型黏粒团或单个黏粒,这些黏粒或黏粒团形状规整、大小比较均匀、排列相对紧密。压缩前的原状样呈絮凝状,并伴有较大的孔隙；压缩后的土样孔隙相对较少,孔隙尺寸分布相对趋于集中(图8(e)和8(f))。由此可知，昔格达半成岩具有较强胶结结构特征。

图8 昔格达土SEM照片Fig.8 SEM photographs of Xigeda soil

2.4 微观结构定量分析

2.4.1 颗粒定量指标

土的微观结构由土颗粒以及土中孔隙相互组合而成,通过IPP软件对1#、2#昔格达原状土SEM照片中的颗粒进行定量化分析,结果列于表3。因为选取的SEM照片倍数相同,所以观测面积基本一致。由表3可以看出: 1#昔格达土的颗粒平均面积约为2#昔格达土的1/2,平均周长约为2#昔格达土的0.43倍,平均长轴长度和平均短轴长度均比2#昔格达土略短,但是两者的颗粒相对面积却相差无几，要解释这一现象需要充分考虑两种昔格达土的矿物成分和颗粒级配,虽然2#昔格达土的黏粒含量较1#的略高,但是2#昔格达土较1#昔格达土缺少蒙脱石和高岭石等黏土矿物,且2#昔格达土石英、钠长石等原生矿物含量超过80%。

表3 昔格达原状土颗粒定量指标

2.4.2 圆形度、形状系数与定向概率熵

施斌[19]在对黏土结构的研究中定义了土体结构单元体排列的定向概率熵(Hm),以反映土体微观结构单元体排列的有序性,Hm越小表明单元体排列方向越一致,有序性越高,反之则越低。圆形度(R)是用来描述颗粒形状和圆形的接近程度的,该值越接近于1,表示颗粒的形态越接近于圆形。形状系数(F)为颗粒等面积圆周长与颗粒实际周长的比值,取值范围为0～1,越接近1,表明颗粒形状越规则。两种昔格达原状土的圆形度、形状系数和定向概率熵如表4所示。

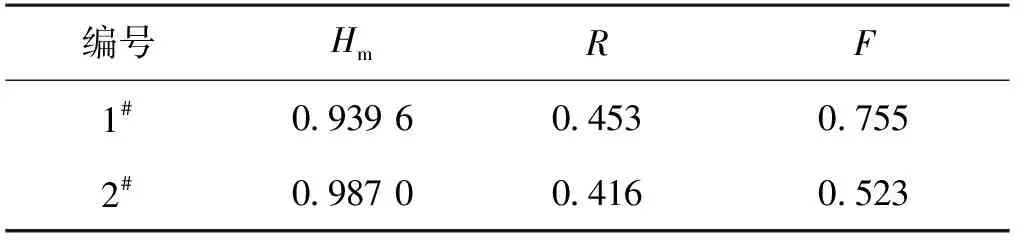
表4 昔格达原状土的圆形度、形状系数和定向概率熵

由表4可知:1#昔格达土的定向概率熵比2#昔格达土的定向概率熵略小,形状系数却比2#昔格达土的形状系数大,这表明1#昔格达土较2#昔格达土方向性更一致,形状更加规则,这与1#昔格达土受到了更大的先期固结压力有关。1#与2#昔格达土圆形度相差不大,这表明1#和2#昔格达土均为扁平状颗粒,与SEM照片观测结果一致。

2.4.3 表面分形维数

自分形理论被提出后,研究人员试图利用分形工具来探索无规则现象所隐含的规律和物理机制。表面分形维数(Dr)是反映颗粒或者孔隙的排列分布密度和形态复杂性的指标,该值越大表明土体中颗粒或孔隙的排列越分散,集团化程度越低,数值范围一般为1～2[20],常用于对无规则形状的微观物体进行定量描述。

通过IPP软件计算出不同固结压力下的颗粒表面分形维数,进而得到的1#昔格达原状土在不同固结压力下的Dr分布概率直方图,如图9所示。

由图9可知:所得Dr范围约为1.05～1.40。Dr在应用中一般将所有颗粒的分形维数取平均值。表面分形维数的频率正态分布曲线的峰顶所在位置为期望值,反映了样本众数。所以本文利用期望值作为评价指标,能较为全面地反映样品的整体不规则程度。图10为不同固结压力下1#原状样土体的表面分形维数正态分布拟合曲线。由图10可以看出:不同固结压力下的颗粒表面分形维数期望值略有不同,且有向更小表面分形维数移动的趋势;且随着固结压力的增大,样品表面分形维数众数所占比例越来越大,表明颗粒在固结压力的挤压下,形状和长轴方向趋于一致。

为了更直观地分析昔格达土颗粒表面分形维数随固结压力变化的规律,本文对表面分形维数与固结压力之间的关系进行了分析(图11)。由图11可知：在到达先期固结压力之前,土体随着固结压力的增大而持续压实,故而表面分形维数不断减小;500 kPa时，试样结构崩溃,土样内部发生崩塌,孔隙变大,表面分形维数短暂上升;而随着固结压力的进一步加大,土样继续被压缩,表面分形维数恢复下降趋势。图12为1#昔格达土固结压力与表面分形维数的关系。由图12可以看出:表面分形维数和固结压力线性负相关,且重塑土比原状土的表面分形维数下降速率更快。

图9 不同固结压力下1#昔格达原状土的表面分形维数分布概率直方图Fig.9 Histogram of distributed probability of surface fractal dimensions of 1# Xigeda original soil under different consolidation pressures

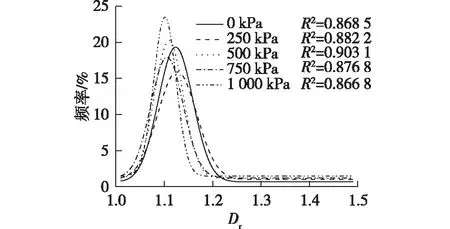
图10 不同固结压力下1#昔格达原状土的表面分形维数正态分布拟合曲线Fig.10 Fitting curves of normal distribution of surface fractal dimension of 1# Xigeda original soil under different pressures

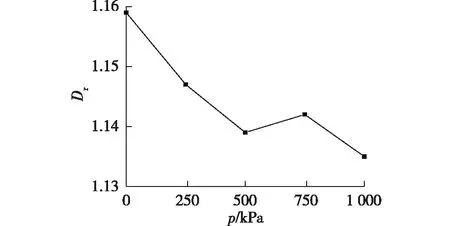
图11 1#昔格达原状土固结压力和表面分形维数的关系Fig.11 Relationship between consolidation pressure and surface fractal dimension of 1# Xigeda original soil

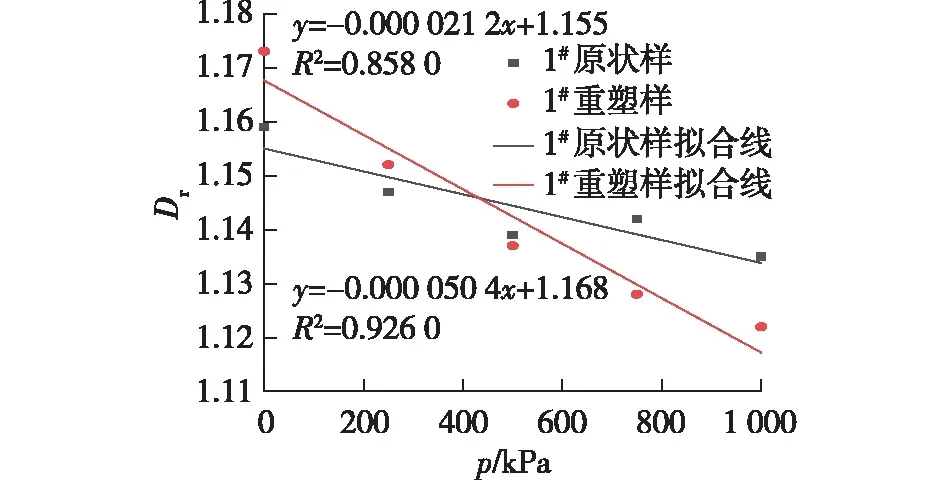
图12 1#昔格达土固结压力与表面分形维数的关系Fig.12 Relationship between consolidation pressure and surface fractal dimension of 1# Xigeda soil

2.4.4 丰度

丰度(C)是指颗粒的短轴与长轴长度之比,反映了颗粒在二维平面内的特征,数值范围为0～1。当丰度趋近于0时,说明颗粒趋向于长条形;当丰度趋近于1时,说明颗粒趋近于正方形。

表5为1#重塑样在不同固结压力下各分度范围的频率分布。由表5可知:颗粒丰度主要集中范围为0.4～0.8,这与SEM照片上颗粒的片状结构相对应。当固结压力为0 kPa、0≤C<0.2时对应的频率为5.82%，而1 000 kPa、0≤C<0.2时对应的频率为7.00%；同时1 000 kPa、0.2≤C<0.4时对应的频率与500 kPa、0.2≤C<0.4时对应的频率相比增长了2.04倍,这说明固结压力的增大使颗粒形状趋向于长条形。

2.4.5 定向性特征

图13为1#昔格达土Hm和av1-2关系曲线。由图13可以看出:昔格达土的Hm与av1-2间呈线性相关。1#原状样的Hm与av1-2关系曲线呈明显的三段式,在低压条件下，原状土颗粒由于受到先期固结压力作用,颗粒定向性更高、排列更有规律、压缩性较高,定向概率熵较小、下降快;但随着固结压力的增大,1#原状样的结构性开始发挥作用,颗粒在固结压力作用下转向所需的能量比无序状态下的重塑样所需能量更多,所以原状样的压缩能力减弱,定向概率熵下降的速率减小；当施加的固结压力足够大时,原状样结构被破坏,重新变得易于压缩,定向概率熵的下降速率又增大。1#重塑样的曲线斜率则一直保持稳定。

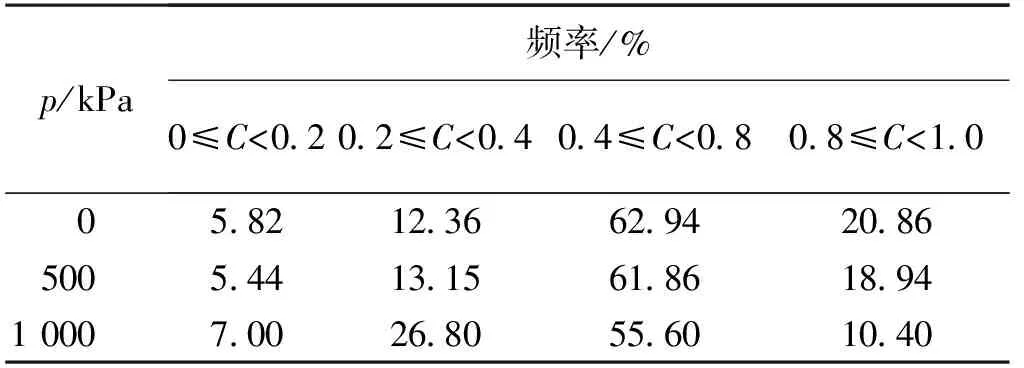
表5 1#重塑样颗粒丰度值分析结果

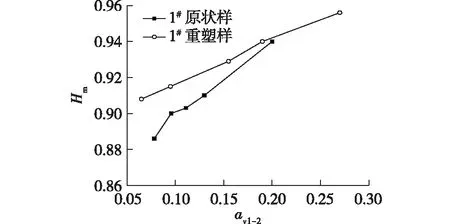
图13 1#昔格达土定向概率熵与压缩系数的关系Fig.13 Relationship between directional probability entropy and compressibility of 1# Xigeda soil

3 结论

1)基于颗粒筛分试验,比较两处不同地点的昔格达土样品,发现两者的黏粒含量都很高,且2#昔格达土的黏粒含量比1#昔格达土的多。通过XRD试验发现两种昔格达土矿物成分存在差别,2#昔格达土与1#昔格达土相比缺少矿物蒙脱石和高岭石。

2)1#昔格达土的压缩曲线属于典型的先缓后陡型,加载至500 kPa后结构破坏;2#昔格达土没有明显的结构屈服点,且高压处原状土和重塑土曲线没有表现出重合趋势。

3)结构参数随着固结压力的变化呈现规律性的变化。在100～500 kPa这一很小范围内，综合结构参数处于一个极不稳定的状态,产生较大变形；而当固结压力大于800 kPa时,则土体进入稳定状态。

4)昔格达半成岩呈开放式的絮凝结构,骨架松散,颗粒定向度较高,片状黏土矿物组成聚集体,具有较强的胶结结构特征。

5)试样的表面分形维数与加压条件直接相关,试样结构破坏后,表面分形维数与固结压力呈负线性相关关系。原状土的定向概率熵与压缩系数曲线呈现明显的三段式结构。