湿热环境下纤维增强树脂-泡桐木夹芯结构Ⅰ型剥离理论分析

高 铭,赵鹏飞,方 园,霍瑞丽,方 海

(南京工业大学 土木工程学院,江苏 南京 211800)

纤维增强树脂(FRP)-轻木夹芯结构是一种以树脂为胶黏剂,集面板、芯材和胶黏剂良好性能于一体的三明治夹芯结构。FRP-轻木夹芯结构不仅具有纤维增强树脂面板的高强度、耐疲劳等优良性能,还兼具芯材的环保、轻质、消音等优良性能。此外,FRP-轻木夹芯结构的面板、芯材以及胶黏剂的种类多样,可根据实际工程中结构性能的需求来对FRP-轻木夹芯结构的组成材料进行组合或改性。因此,FRP-轻木夹芯结构得以在桥梁、海洋工程、船舶等领域迅速崭露头角,并得到广泛的应用与研究[1-4]。FRP-轻木夹芯结构的性能与组成材料的自身缺陷、制造工艺、使用环境等有关,FRP-轻木夹芯结构多应用于温差大、湿度大的恶劣环境中,这会减弱芯材和面板界面间的黏结作用;当结构长期处于这种环境中,结构的初始细微缺陷会逐渐变大,降低结构的性能与使用寿命,可能导致结构的失效[5]。文献[6-8]研究表明:芯材和面板界面间的黏结作用下降和界面的剥离损伤是夹芯结构性能降低、寿命下降甚至失效的主要原因,其中界面剥离损伤中Ⅰ型界面剥离占据主要部分。因此，需对夹芯结构的Ⅰ型界面剥离行为进行研究,以便于根据研究结果采取措施来减小界面剥离行为产生的不良影响。

Siriruk等[9]通过试验和有限元分析研究了泡沫夹芯结构在海水环境中的界面分层行为,试验结果表明,当夹芯结构持续暴露在海水中一段时间后,界面的断裂韧性下降30%,裂纹向芯材与面板界面处逐渐扩展,而无海水处理的夹芯结构的裂纹在芯材中扩展。Pradeep等[10]以弹性地基梁模型为基础,同时考虑了蜂窝夹芯结构双悬臂梁(DCB)试件上、下臂的不同地基模量,采用柔度分析法推导了试件的临界应变能释放率的计算公式,并将试验值和有限元分析的结果进行对比来验证计算方法的有效性,研究结果表明,考虑不同地基模量后的计算方法的准确性相比传统方法得到了提高。Wang等[11]通过DCB试验研究了温度对泡沫夹芯结构Ⅰ型界面断裂行为的影响,并提出了考虑温度、热变形等因素的泡沫夹芯结构Ⅰ型界面能量释放率的分析模型,结果表明,能量释放率及剥离荷载与温度呈负相关关系,所建立的分析模型在一定程度上可以用于估计夹芯结构的能量释放率。Wang等[12]研究发现,采用短切玻璃纤维对夹层梁增强后,夹层梁的界面韧性、抗界面裂纹扩展能力和抗损伤能量均得到了提高。施冬等[13]通过拉挤成型工艺制备了玻璃纤维增强树脂(GFRP)-泡桐木夹芯板,并研究了构件的制备工艺和芯材表面是否开槽对界面性能的影响,研究发现,开槽后拉挤成型工艺制备的构件的界面能量释放率得到了提高,而不开槽时拉挤成型工艺制备的构件的界面性能更好。综上所述,现阶段主要研究了泡沫夹芯结构和蜂窝夹芯结构的界面破坏行为,而轻木夹芯结构研究较少，但FRP-轻木夹芯结构在湿热环境下的界面韧性和破坏行为的研究具有重要意义。

FRP-轻木夹芯结构的芯材主要有Balsa木和泡桐木,泡桐木除密度略大于Balsa木外,其他性能均表现良好,且价格低、环保、易获取[14]。因此，本文以FRP-泡桐木夹芯结构为研究对象,研究泡桐木夹芯结构在湿热环境下的Ⅰ型界面韧性,并基于弹性地基梁模型进行Ⅰ型临界能量释放率公式的推导,将试验所得值与理论计算值进行对比,验证所推导公式的准确性。

1 试验

1.1 试验材料和试件制备

本次试验的FRP-泡桐木夹芯结构试件以E型无碱玻璃纤维布为面板、密度约为250 kg/m3的泡桐木为芯材、乙烯基树脂为胶黏剂。试件采用手糊成型工艺制备,并在泡桐木芯材表面一侧引入长50 mm、与芯材等宽的预裂纹。根据规范ASTM D1781:1998和ASTM D1761:1998确定FRP-泡桐木夹芯结构试件的面板尺寸和芯材尺寸分别为254 mm×80 mm×2 mm和254 mm×80 mm×25 mm。

1.2 人工加速老化试验方案

通过调节湿热试验箱的温度加速老化试验,湿热试验箱内相对湿度稳定在93%,温度变化以24 h为一个周期:2 h内从20 ℃升温到60 ℃;60 ℃恒定温度10 h;2 h内温度降低至20 ℃;20 ℃恒定温度10 h。老化试验共计进行180 d,以0、15、30、60、90、120、150、180 d为时间节点,每个时间节点取5个泡桐木芯材试件、10个GFRP面板试件、5个FRP-泡桐木夹芯结构试件。当达到预定的老化时间时,将试件取出分别进行组分材料的弯曲试验和夹芯结构试件的DCB试验。

1.3 DCB试验

将达到预定老化时间的夹芯结构试件从湿热试验箱中取出,在室温下放置24 h,然后将尺寸为80 mm×40 mm×20 mm的加载块黏结在试件的预裂纹一端,并与试件边缘对齐,加载块在黏结前要进行打磨和去污处理。试件的尺寸和加载块的位置如图1所示。

图1 双悬臂梁试件尺寸(mm)Fig.1 Specimen dimension of DCB (mm)

双悬臂梁Ⅰ型界面剥离试验在CMT5805型万能试验机(量程20 t)上完成,试验的加载速度为2 mm/min。加载示意如图2所示,图中P为施加的荷载,L为试件长度,h1为GFRP面板厚度,h2为泡桐木芯材厚度,δ为裂纹的张口宽度(δ=δ1+δ2),a为试件破坏时的裂纹深度。

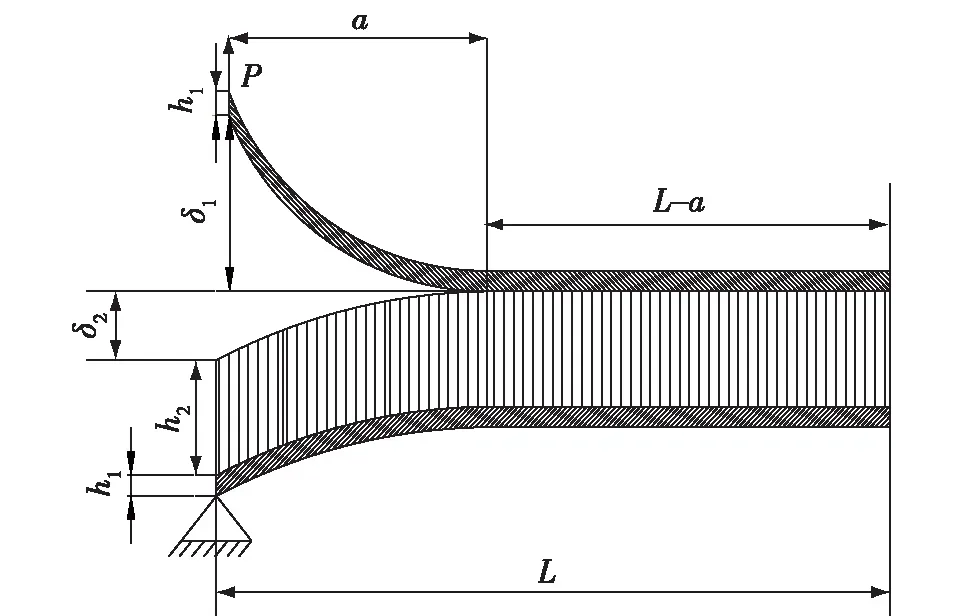
图2 DCB加载示意图Fig.2 Schematic diagram of loading of DCB tests

2 结果与分析

2.1 FRP-泡桐木夹芯结构组分材料的力学性能衰减规律

FRP-泡桐木夹芯结构的泡桐木芯材的弯曲模量(Ec(t))和GFRP面板的弯曲模量(Ef(t))随湿热老化时间(t)的变化规律分别如图3和4所示。由图3和4可知:湿热环境下泡桐木芯材和GFRP面板的弯曲模量随着老化时间的延长均呈先增大后减小的趋势。当老化时间为15 d时,由于乙烯基树脂的后固化作用,泡桐木芯材和GFRP面板的弯曲模量增至最大;15 d后泡桐木芯材和GFRP面板的弯曲模量在湿热老化环境下逐渐下降。0～15 d泡桐木芯材和GFRP面板的弯曲模量呈折线分布,仅有两个数据点,直接采用直线表示。15 d后泡桐木芯材和GFRP面板的弯曲模量呈曲线分布,采用Williams模型进行试验数据的拟合[15]，拟合得到的计算公式见式(1)和(2),拟合曲线如图3和4所示。泡桐木芯材和GFRP面板弯曲模量拟合曲线的相关系数分别为0.965和0.989,具有较高的可靠性。

(1)

(2)

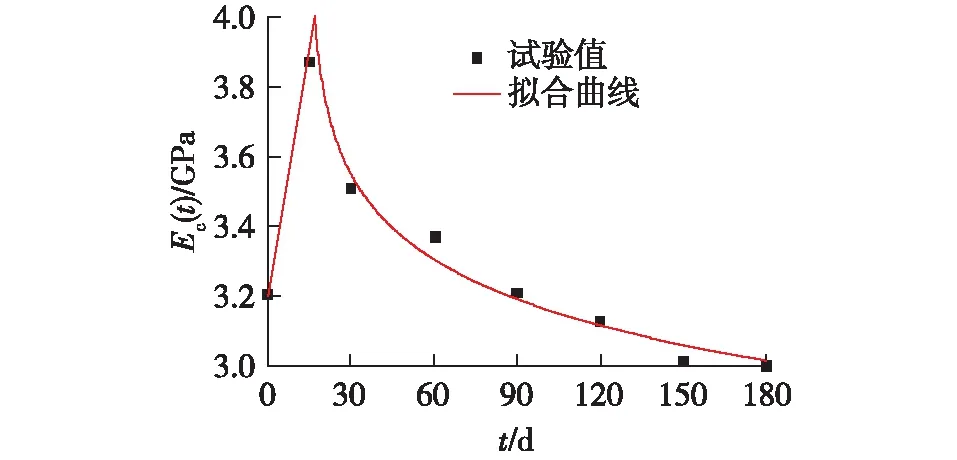
图3 湿热环境下泡桐木芯材弯曲模量的变化规律Fig.3 Flexural modulus change rules of paulownia wood in hygrothermal environment

图4 湿热环境下GFRP面板弯曲模量的变化规律Fig.4 Flexural modulus change rules of GFRP face sheet in hygrothermal environment

2.2 FRP-泡桐木夹芯结构的DCB试验结果与分析

2.2.1 FRP-泡桐木夹芯结构的裂纹扩展

湿热环境下FRP-泡桐木夹芯结构的荷载-位移曲线如图5所示。由图5可知:裂纹扩展整体呈由稳定到不稳定再逐渐稳定的趋势。夹芯结构未老化时,裂纹稳定扩展，荷载达到最大值后随着位移的增加缓慢下降直至试件破坏,荷载-位移曲线未出现明显波动;湿热老化15 d时，夹芯结构的胶黏剂乙烯基树脂可能存在部分未完全固化,界面黏结作用不均匀,出现应力集中现象,裂纹开始出现轻微的不稳定扩展,荷载随着位移的变化出现了小幅度的波动;湿热老化30 d时，泡桐木芯材经过湿热环境老化作用后部分发生变形,出现应力集中现象,曲线波动幅度增加且达到荷载最大,裂纹的扩展最不稳定;从湿热老化60 d开始,曲线波动幅度明显减小,裂纹扩展趋于稳定。此外,在相同的位移下,荷载随着湿热老化时间的延长也呈不稳定变化。试验过程中发现,在位移为1 mm左右时,湿热老化15和180 d的荷载出现短时间激增的现象,其中湿热老化180 d的荷载峰值为325 N,比湿热老化15 d时的大了100 N,芯材腐蚀严重,界面黏结作用下降。

图5 湿热环境下FRP-泡桐木夹芯结构荷载-位移曲线Fig.5 Load-displacement curves of FRP-paulownia wood sandwich structure in hygrothermal environment

2.2.2 FRP-泡桐木夹芯结构的临界能量释放率

夹芯结构的界面韧性常用能量释放率来衡量,可采用屈服刻度法计算DCB试验试件的Ⅰ型临界能量释放率(GI)[16],见式(3)。

(3)

式中:B为夹芯结构宽度;n为试验参数,可利用origin软件对lgC和lga进行最小二乘拟合确定,C为夹芯结构的柔度。

由DCB试验得到不同老化时间、不同裂纹深度下夹芯结构的临界能量释放率如图6所示。根据图6可知:临界能量释放率随老化时间的延长总体上呈先增大后减小的趋势;老化时间一定时(除30 d外),临界能量释放率随裂纹宽度变化而变化的幅度很小。30 d时裂纹扩展不稳定,临界能量释放率的变化幅度较大且不断波动,变化幅度达371.03 J/m2,这是由于30 d时老化环境的腐蚀作用生效,芯材在老化箱中出现部分变形,并且此时老化箱中的温度接近树脂的玻璃化转变温度,树脂从玻璃态向高弹态转变,在荷载稳定变化的情况下位移迅速增大,从而导致了临界能量释放率的迅速增长。从60 d开始,临界能量释放率呈下降趋势,其值也小于未老化夹芯结构的临界能量释放率。180 d时临界能量释放率平均值已经下降至78.69 J/m2,相比未老化夹芯结构下降了41.86%。综上可知,湿热环境对FRP-泡桐木夹芯结构的界面韧性具有明显的不利影响。

图6 不同老化时间临界能量释放率随裂纹深度的变化(DCB试验结果)Fig.6 Variation of energy release rate at different ageing time with crack depth (result of DCB tests)

2.3 FRP-泡桐木夹芯结构的Ⅰ型界面剥离理论

2.3.1 基于弹性地基梁模型的Ⅰ型临界能量释放率公式

夹芯结构界面断裂韧性的理论研究已经取得了很多成果,关于DCB试件界面韧性的理论研究方法主要包括:Levinson梁理论[17]、弹性地基梁模型[18-19]等,其中弹性地基梁模型应用较广泛。因此,笔者将以弹性地基梁为基础,利用Timoshenko和Goodier[20]提出的悬臂梁理论来考虑剪切变形的影响,同时考察温度、湿度和时间对能量释放率的影响,并以此来推导湿热环境下FRP-泡桐木夹芯结构的Ⅰ型临界能量释放率计算公式。FRP-泡桐木夹芯结构DCB弹性地基梁模型如图7所示。

图7 夹芯结构弹性地基梁模型Fig.7 Elastic foundation beam model of sandwich structures

Ⅰ型临界能量释放率可由式(4)计算[21]。

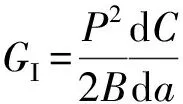
(4)

夹芯结构试件的柔度可根据式(5)计算[18]。

(5)

式中:δ(-a)是某时刻裂纹深度x=-a处试件的张口宽度。

夹芯结构界面的张口宽度与裂纹深度存在关系,可通过两者的关系获得试件的柔度公式,从而得到Ⅰ型临界能量释放率的计算公式。张口宽度和裂纹深度之间的关系见式(6)[18-19]。

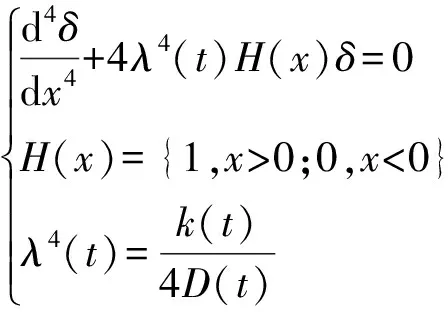
(6)

式中:x为某时刻的裂纹深度,D(t)为DCB试件的一维耦合刚度,k(t)为模型的地基模量,D(t)和k(t)与老化时间有关。

引入参数ci(i=1～8),并根据式(6)和边界连续条件可得到张口宽度与裂纹深度的基本关系,见式(7)。

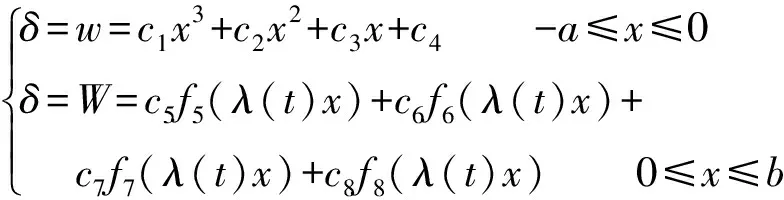
(7)

式中:f5(Γ)=eΓcosΓ,f6(Γ)=eΓsinΓ,f7(Γ)=e-ΓcosΓ,f8(Γ)=e-ΓsinΓ,Γ=λ(t)x。

根据弹性地基梁模型的边界条件可以求出ci(i=1～8),边界条件见式(8)。

(8)

式中:I为截面惯性矩。

将边界条件代入式(7),可得式(9)—(16)。

(9)

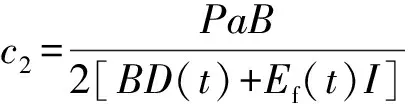
(10)

c4-c5-c7=0

(11)

c3-λ(t)c5-λ(t)c6+λ(t)c7-λ(t)c8=0

(12)

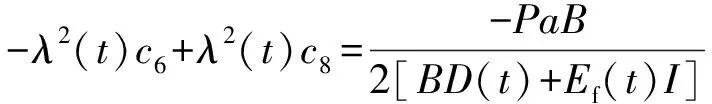
(13)

(14)

(15)

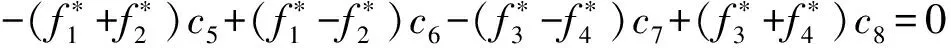
(16)

将式(9)—(16)相结合可求出式(7)中的未知数,再根据式(7)求出δ(-a)并代入式(5),可得到未考虑剪切变形的夹芯结构的柔度计算式,见式(17)。

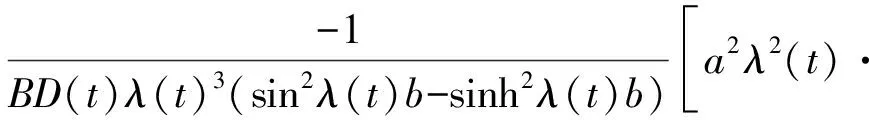
(coshλ(t)bsinhλ(t)b+sinλ(t)bcosλ(t)b)+

(17)

考虑剪切变形后,式(17)变为式(18),其中GFRP面板的剪切模量(Gf(t))见式(19)。将式(18)代入式(4)得FRP-泡桐木夹芯结构的Ⅰ型临界能量释放率,见式(20)。

(18)

(19)

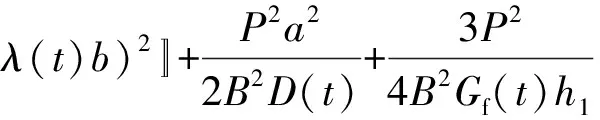
(20)

式中:υf为GFRP面板的泊松比。

D(t)和k(t)可根据式(21)—(24)计算[11,22]。式(21)—(24)中面板和芯材的弯曲模量随着老化时间变化,可根据湿热环境下GFRP面板和泡桐木芯材的力学性能衰减规律获得。

(21)

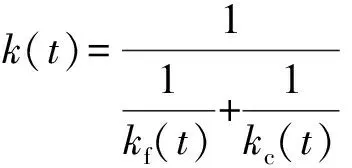
(22)

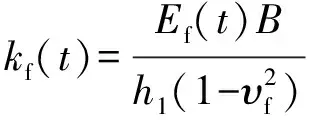
(23)

(24)

式中:kf(t)为GFRP面板贡献的地基模量,kc(t)为泡桐木芯材贡献的地基模量。

2.3.2 理论值与试验值的对比

根据式(20)计算出Ⅰ型临界能量释放率的理论值(图8),并将Ⅰ型临界能量释放率随裂纹深度变化的理论值与DCB试验值(图6)进行对比。由图8可知:Ⅰ型临界能量释放率理论值的整体变化趋势和试验值相同,在30 d前Ⅰ型临界能量释放率随湿热老化时间的延长呈增加趋势,从60 d开始Ⅰ型临界能量释放率随湿热老化时间的延长而降低,180 d时降至79.65 J/m2,相比未老化时下降了48.31%。

图8 不同老化时间临界能量释放率的理论值随裂纹深度的变化(式(20)计算结果)Fig.8 Varation of theoretical values of energy release rate at different ageing time with crack depth(result of formula 20)

相同湿热老化时间下FRP-泡桐木夹芯结构Ⅰ型临界能量释放率随裂纹深度变化相差不大，因此取平均值进行试验值和理论值对比,结果见图9。根据图8和9可知:老化时间为30 d时,裂纹不稳定扩展,Ⅰ型临界能量释放率的试验值和理论值的相对误差较大,但是30 d时Ⅰ型临界能量释放率随裂缝深度变化的理论值比试验值更加稳定。老化时间为60 d时,相对误差较30 d稳定。30 d时夹芯结构Ⅰ型平均临界能量释放率的试验值和理论值分别为284.94和220.53 J/m2,60 d时夹芯结构Ⅰ型平均临界能量释放率的试验值和理论值分别为107.50和150.52 J/m2,30和60 d试验值与理论值的相对误差均超过了20%。除30和60 d外,其他老化时间的夹芯结构Ⅰ型平均临界能量释放率的试验值与理论值的误差基本小于15%，相对误差均处于合理范围内。这是由于下面板和泡桐木芯材组成的地基的位移在公式推导过程中被忽略,并且泡桐木的线弹性变形能力差,受弯时进入弹塑性状态较快,这使得夹芯结构Ⅰ型临界能量释放率的理论值和试验值产生了误差。

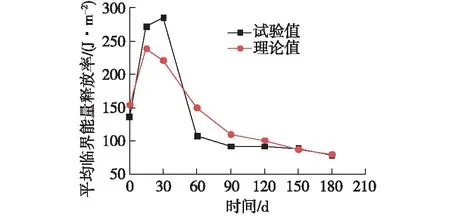
图9 平均临界能量释放率试验值与理论值对比Fig.9 Comparison between experimental and theoretical value of energy release rate

湿热环境老化后期的理论值大于试验值,但试验值与理论值的变化趋势大体一致,相对误差也处于合理范围内。因此,基于弹性地基梁模型的考虑剪切变形和湿热环境影响的Ⅰ型临界能量释放率计算公式对于湿热环境下FRP-泡桐木夹芯结构的Ⅰ型临界能量释放率的估算具有一定的准确性。

3 结论

1)根据DCB试验的荷载-位移曲线和临界能量释放率随裂纹深度变化可知:FRP-泡桐木夹芯结构未老化时裂纹扩展稳定;湿热环境老化后,裂纹的扩展随老化时间的延长呈由稳定到不稳定再到稳定的趋势。

2)FRP-泡桐木夹芯结构临界能量释放率的试验值随老化时间的延长呈先增加后降低的趋势,180 d时临界能量释放率比未老化时降低了41.86%,表明湿热环境对FRP-泡桐木夹芯结构的界面韧性影响较大。

3)基于弹性地基梁模型推导了考虑剪切变形的FRP-泡桐木夹芯结构的Ⅰ型临界能量释放率公式,并将试验值与理论值对比,发现两者具有一定的吻合性,可用于估算FRP-泡桐木夹芯结构在湿热环境下的Ⅰ型临界能量释放率。