基于自由曲面的空间光学系统偏振像差分析

张艺蓝，史浩东，王 超，李英超，刘 壮，张 肃，王稼禹，姜会林

（长春理工大学 光电工程学院，吉林 长春 130022）

1 引言

随着空间技术的不断发展，对空间观测的精度和要求也不断提高。偏振探测可以滤除背景杂光，提高成像对比度和测量精度。但偏振像差会影响系统的成像质量和测量精度［1］。虽然离轴自由曲面光学系统能够突破传统同轴光学系统的瓶颈，实现大孔径、大视场和长焦距，但同时也引入了非旋转对称的偏振像差。因此，掌握自由曲面对离轴光学系统的偏振像差作用机理，有助于掌握和调控光学系统的偏振像差分布，进而满足卫星探测识别时的高精度成像需求。

国外对偏振像差的研究起步较早。1987 年，Chipman 提出了偏振像差理论，并通过琼斯矩阵的特征值分解出二向衰减和相位延迟像差［2］。1994 年，Mcguire 等将偏振像差函数分解并扩展成偏振像差矩阵，对旋转对称系统进行了偏振像差分析［3］。2014 年，Sasian 从场和波阵面的角度解释了偏振像差［4］。2015 年，Chipman 等人分析了偏振像差对天文望远系统成像质量的影响［1］。国内近年来针对光学系统的偏振效应开展了研究［5-7］。2009 年，张颖等人研究了透射式旋转对称系统的偏振效应［8］。2013 年，宣斌等人分析了光的偏振正交性对提高线偏振相移干涉检验精度的作用［9］。2017 年，杨宇飞等人分析了相干激光通信系统的偏振像差［10］。2020 年，罗敬等人研究了离轴天文望远镜的偏振像差，并分析了偏振像差对光学椭率的影响［11］。然而，目前还没有针对自由曲面离轴光学系统偏振像差特性的理论建模和分析，设计者仍难以预判偏振像差对此类光学系统成像质量的影响，大大降低了偏振成像系统的设计效率。因此，研究离轴自由曲面光学系统的偏振像差分布特性不仅能够进一步完善偏振像差理论体系，而且对自由曲面在离轴偏振成像系统中的应用具有重要的指导意义。

本文基于琼斯表示方式，构建了以条纹Zernike 多项式为表征函数的自由曲面离轴光学系统偏振像差解析模型，通过对琼斯矩阵的分解，分析了条纹Zernike 多项式第5 项到第9 项等低阶系数对视场离轴光学系统相位像差、相位延迟和二向衰减等偏振像差分布的影响，并根据理论分析设计了含有自由曲面的大视场非旋转对称三反系统，为后续探索利用自由曲面调制离轴光学系统偏振像差提供了理论基础。

2 基本理论

本文主要研究光学系统中偏振光相位和振幅的相对变化，与穆勒矩阵相比，琼斯表示法可以更直观地表现相位像差、二向衰减、相位延迟像差与自由曲面之间的关系。所以采用以琼斯矢量和琼斯矩阵为基础的偏振理论进行研究［12］。

其中：ck为σk的系数，ρk和ϕk分别对应ck的实部和虚部。通常用一个琼斯矩阵描述经过光学元件的整个光束截面。光学系统沿着不同光路的这种偏振变化可以用偏振像差函数J(h，ρ，λ)来表示：

其中：J表示与光路有关的琼斯矩阵，它是关于物坐标h，孔径坐标ρ和波长λ的函数。偏振像差函数J(h，ρ，λ)完整地描述了光学系统的偏振特性，其中的相位项ϕ0(h，ρ，λ)与几何光学的波像差函数W(h，ρ，λ)之间的关系为［13］：

McGuire 于1994 年提出了离轴系统偏振像差的矢量表达式［12］，可以表示系统中光学元件对偏振像差贡献之和，如式（5）所示：

其中：Ptuvwx=Αtuvwx+iΦtuvwx，表示偏振像差系数，Αtuvwx和Φtuvwx分别是Ptuvwx的实部和虚部，t表示偏振的类型，u表示对视场H依赖性的阶数，v表示对ρ依赖性的阶数，w表示对入瞳坐标(ρ，ϕ)中角度ϕ的依赖性，x表示线性二向衰减与相位延迟的方向关于入瞳坐标(ρ，ϕ)中角度ϕ的阶数。

偏振像差函数可通过泡利分解，分解为振幅像差、相位像差、相位延迟和二向衰减［14］。其中，振幅像差主要与系统中元件的透过率有关，本文不做研究；相位像差与光程差关系密切，自由曲面的引入会直接改变光程差，因此自由曲面对相位像差的影响不可忽略；相位延迟和二向衰减像差与光线入射角度等因素有关，由于自由曲面面形的非旋转对称性，光线入射角会发生微量的变化。因此，研究离轴自由曲面光学系统的偏振像差特性，其本质是对相位像差、相位延迟以及二向衰减进行深入的分析和计算。

3 自由曲面偏振像差建模

自由曲面的多自由度特点导致界面上各点光线的入射角度不同，自由曲面的引入也会改变系统整体的偏振矩阵表征。本文基于条纹Zernike 多项式表示自由曲面面形，解析自由曲面与相位像差之间的关联，运用自由曲面偏振光线追迹算法，得到全视场全口径的二向衰减和相位延迟的分布，从而分析自由曲面对整个系统琼斯矩阵的影响。

3.1 自由曲面相位像差建模

Zernike 多项式对非旋转对称表面的全局面形拟合能力较强，通常选用Zernike 多项式表征自由曲面的面形特征。

根据式（4）可知，波像差与相位像差有定量的关系，而自由曲面面型的多自由度会不同程度地影响系统的光程差，进而影响波像差。因此，本文通过波像差将条纹Zernike 多项式表示的自由曲面与相位像差相关联，将Zernike 多项式的表达式矢量化，利用波像差理论对Zernike 多项式自由曲面产生的像差进行解析，进而找到Zernike 自由曲面与相位像差之间的关系，从而建立Zernike 多项式自由曲面的相位像差分析方法。

首先，将原本用极坐标表示的Zernike 多项式矢量化。Zernike 多项式自由曲面的高阶震荡部分可以表示为：

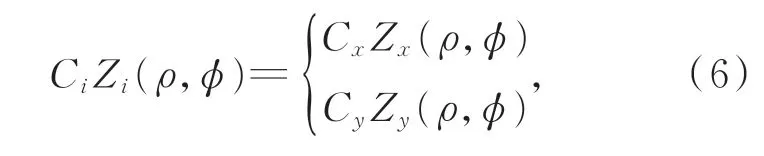
其中：Cx和Cy是一组Zernike 多项式系数。通过对Zernike 多项式进行变换，结合矢量乘法法则，可以将Zernike 多项式中的每一组系数进行矢量化，得到：

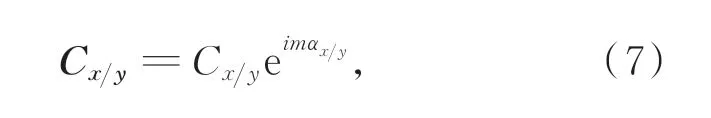
在这里已对进行修正，规定表示在右手坐标系下始于+Y轴方向顺时针旋转的角度。

众所周知，波像差的本质是由光程差引起的。同样，自由曲面引入波像差的本质应该也是由面形带来的光程差异。这里以一个反射自由曲面表面为例，对该面产生的光程差进行说明，如图1 所示。当入射光线角度不是很大时，入射和出射光线的光程均可等效为入射点的面形矢高，则入射光线和出射光线的光程差可以表示为：

图1 Zernike 多项式的面形矢高Fig.1 Surface vector height map of Zernike polynomial terms

其中：n1和n2为入射和出射光线所在的介质折射率，λ为波长，Z(ρ)为根据公式矢量化后的Zernike 多项式。为方便表示，令，则：

根据偏振像差函数J(h，ρ，λ)中的相位项ϕ0(h，ρ，λ)与几何光学波像差函数W(h，ρ，λ)之间的关系，则当自由曲面远离光阑位置时，自由曲面的相位像差的贡献量为：

需要特别注意的是，光学系统的波像差分布与光阑位置密切相关。因此，相位像差分布也与光阑位置密切。在入瞳直径不变的情况下，当光阑位置分别位于球面和远离球面时，轴外视场光线经光阑入射到反射镜上的区域之间存在一个光瞳偏移矢量Δh，该偏移矢量将使光学系统的相位像差重新分布，如下：

当视场角不是很大时，偏移矢量与视场成线性的关系可表示为：

其中：yˉ表示轴外视场主光线的入射高度，y表示轴外视场边缘的光线高度。

当光阑与自由曲面位置重合时，可以看成是远离光阑位置的一种特殊情况。此时在同一口径下，各视场光线入射到自由曲面表面的区域均相同，面形对各视场光线的作用也相同，因此自由曲面所产生的相位像差贡献量与视场无关。而当光阑位置远离自由曲面时，由于Δh与视场矢量H相关，所以自由曲面产生的相位像差分布会随视场发生改变。为了能够分析自由曲面在光学系统中任意位置时对相位像差分布的影响，以下将针对远离光阑位置的自由曲面相位像差解析式进行推导。

当自由曲面远离光阑位置时，照射到自由曲面上的光线口径会发生偏移，口径偏移矢量为Δh，此时自由曲面的相位像差贡献量为：

由式（14）可知，虽然Zernike 多项式只与口径有关，但当其远离光阑位置时，其像差贡献量有可能还与视场有关。

为了具体地分析自由曲面所引入相位像差的分布特性，本文对Zernike 多项式的前9 项分布进行分析讨论。这9 项中，前3 项属于纯相位变化，对成像质量没有影响，第4 项表示离焦，可以通过调整像面位置进行消除。因此，本文将运用上述分析流程从第5 项开始逐一分析引入相位像差的分布特性，得到自由曲面项在远离光阑的位置时相位像差ϕ0的表达式为：

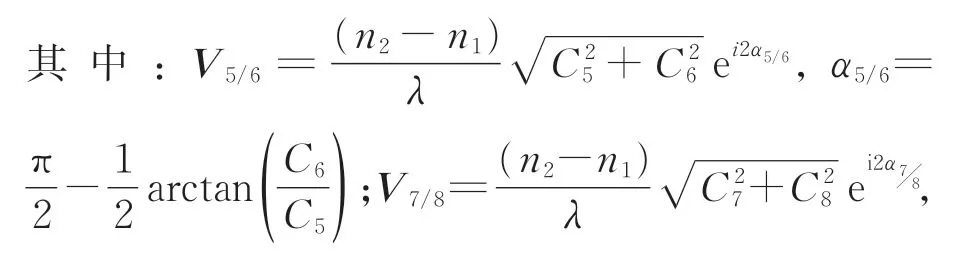
借助光学软件对一个自由曲面单反射镜系统的偏振像差分布进行分析。设反射镜球面半径为100 mm，视场角为2°，将光阑置于距反射镜前50 mm 处时，在反射镜上引入自由曲面，运用光学设计软件与Matlab 对该单反射镜系统进行全口径自由曲面偏振光线追迹，得到自由曲面项对相位像差的影响，如图2 所示。由图2 可以看出项自由曲面面形对相位像差的影响主要是引起像散的变化。相位像差ϕ0的改变主要体现在偏振像散在引入自由曲面前后的变化。项自由曲面面形对相位像差的影响主要是引起偏振像散和偏振彗差的变化。相位像差ϕ0的改变主要体现在偏振像散和偏振彗差在引入自由曲面后的变化上。Z9项自由曲面面形对相位像差的影响主要是引起偏振球差、偏振像散和偏振彗差的变化。相位像差ϕ0的改变主要体现在偏振球差、偏振像散和偏振彗差在引入自由曲面后的变化上。

图2 Zernike 多项式自由曲面对系统偏振像差的影响Fig.2 Influence of freeform surface of Zernike polynomial on polarization aberration of system

3.2 自由曲面引入二向衰减和相位延迟建模

传统偏振光线追迹算法采用二维偏振光线追迹［17-19］，是利用琼斯矩阵表征光学界面的偏振特性［20-22］。由于自由曲面上各个点的法向量都不同，不同角度入射的光线所对应的出射光方向也不相同，在传统的二维矩阵中加入光线的传播矢量k，可以更好地分析含有自由曲面光学系统的偏振特性。这里基于Zernike 自由曲面表达方法，构建自由曲面偏振光线追迹算法，进而分析自由曲面对二向衰减、相位延迟像差的影响。

自由曲面偏振光线追迹与光线的传播矢量k紧密相关。如图3 所示，在自由曲面上，各处的曲率都不相同，入瞳内每个点的入射角不同。根据菲涅尔公式，不同角度入射光中s和p分量的反射率（折射率）发生变化，光线经各个光学元件后，s和p分量的变化会改变出瞳处光束的偏振态，因此，系统的偏振特性与其结构、膜系参数都紧密相关。

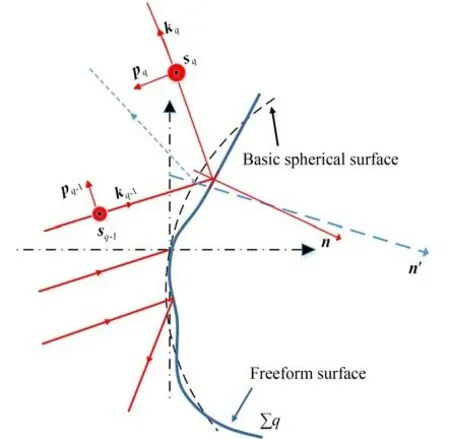
图3 第q 平面上偏振光线折反射示意图Fig.3 Schematic diagram of polarized light refraction and reflection on qth plane

加入传播矢量k的琼斯矩阵是一个3×3 的矩阵Pq，它表示光线经过光学系统各个界面时偏振态的变化。在全局坐标系中，通过自由曲面偏振光线追迹，可以得到表示光学系统对入射光线的偏振变换矩阵Ptotal：

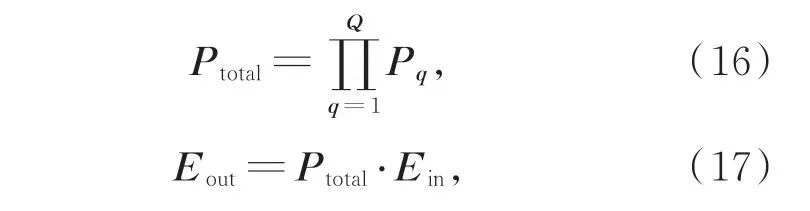
式中：Ein，Eout表征入射和出射光束的琼斯矢量，矩阵Pq表征第q界面对入射光束的偏振态改变，如图3 所示。Pq与光束在光学界面处的k，s和p分量关系为：

式中：as，q，ap，q分别是第q界面s和p分量的振幅透射（反 射）系数；sm，q−1，pm，q−1，km，q−1(m=x，y，z)表示入射光线在全局坐标系中的s，p和k分量的坐标；sn，q，pn，q，kn，q(n=x，y，z)表示出射光线在全局坐标系中的s，p和k分量的坐标。其中，s和p分量为：

针对某一特定方向的入射光束，采用自由曲面偏振光线追迹算法，可以计算系统各个界面对该光束的偏振转换矩阵Ptotal，对Ptotal进行奇异值分解：

偏振变换矩阵Ptotal被分解为两个酉矩阵U，V和一个对角阵D。其中，对角阵D包含的Λ1，Λ2（Λ1≥Λ2）是偏振变换矩阵Ptotal的特征值。矩阵中k0，kQ分别对应入射光传播方向和经过Q次折反射后出射光的传播方向。v1，v2和u1，u2分别对应光学系统入瞳面和岀曈面内的本征偏振态，它们之间满足如下关系：

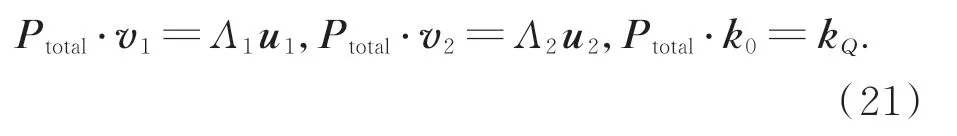
根据二向衰减和相位延迟的定义［23-24］，可以计算出光学系统的二向衰减和相位延迟的大小和方向。对一个自由曲面单反射镜系统的偏振像差分布进行分析。运用光学设计软件与Mat⁃lab 对该单反射镜系统进行全口径自由曲面偏振光线追迹，分别计算出瞳处各光线的偏振变换矩阵Ptotal，通过对矩阵Ptotal进行奇异值分解与变换，可以得到对应点的二向衰减和相位延迟，如图4所示。

图4 表明，该系统的二向衰减和相位延迟像差都随着该点到光轴距离的增大而增大，即轴外视场下光学系统的偏振效应更明显。偏振像差的变化与光学系统的结构密切相关，系统是视场离轴系统，离轴方向在子午面内，该系统的二向衰减图和相位延迟图均失去其旋转对称性。光学系统离轴后，越靠近光轴位置入射的平行光，在光学系统中的入射角度越小，相应的二向衰减和相位延迟量也越小。

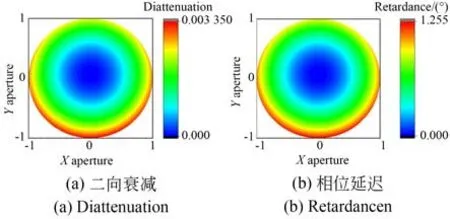
图4 含 项自由曲面单反射系统的偏振像差分布Fig.4 Distribution of polarization aberration of freeform single reflection system with term

为直观展现自由曲面对二向衰减像差和相位延迟像差的影响，将含项自由曲面系统的偏振像差与不含自由曲面系统的偏振像差相减，得到自由曲面加入前后二向衰减和相位延迟的变化，如图5 所示。

由图5 可知，当视场仅在Y轴向上偏移2°时，自由曲面对二向衰减和相位延迟像差都有影响，其分布规律与自由曲面的面形矢高相同。对称轴相对Y轴的旋转角度与Z5项、Z6项系数的关系为

图5 项自由曲面加入后的像差变化Fig.5 Changes of aberrations after adding freeform with term

为了进一步展现视场对自由曲面偏振特性的影响，将该离轴系统中的自由曲面去掉，对它进行全视场自由曲面偏振光线追迹，整理各个视场下得到的二向衰减和相位延迟，与之前含自由曲面时得到的数据对比，得到各个视场下自由曲面项面形对二向衰减与相位延迟的最大改变量，如图6 所示。

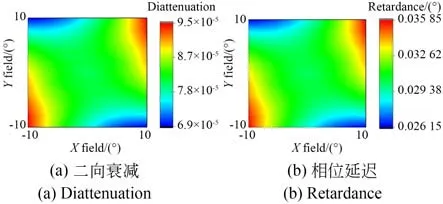
图6 全视场的 项自由曲面对系统偏振像差的影响Fig.6 Effect of freeform with term on polarization aberration in full field of view

由图6 可知，无论是中心视场还是边缘视场，偏振像差都受到了不同程度的影响。其中，二向衰减的最大改变量为9.5×10−5，相位延迟的最大改变量为0.035°。通过以上仿真结果可以看出，自由曲面面形会影响偏振像差的大小和分布。

运用该单反射镜系统分析项和Z9项自由曲面对二向衰减和相位延迟的影响，得到出瞳处对应点的二向衰减、相位延迟的大小（如图7 和8 所示）以及自由曲面加入前后二向衰减和相位延迟的变化（如图9 和图10 所示）。

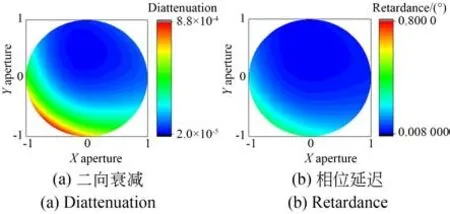
图7 含 项自由曲面单反射系统的偏振像差分布Fig.7 Distribution of polarization aberration of freeform single reflection system with term

图8 含Z9 项自由曲面单反射系统的偏振像差分布Fig.8 Distribution of polarization aberration of freeform single reflection system with Z9 term

图9 项自由曲面加入后二向衰减像差和相位延迟像差的变化Fig.9 Changes of diattenuation and retardance after add⁃ing freeform with term

图10 Z9 项自由曲面加入后二向衰减像差和相位延迟像差的变化Fig.10 Changes of diattenuation and retardance after add⁃ing freeform with Z9 term

图9 和图10 表明，该系统的二向衰减和相位延迟像差在出瞳处的分布是轴外视场下光学系统的偏振效应与自由曲面的矢高共同作用的结果。偏振像差的变化与光学系统的结构密切相关，视场离轴系统的离轴方向在子午面内，该系统的二向衰减图和相位延迟图均在子午面内有所偏移。自由曲面对二向衰减和相位延迟的分布规律与项和Z9项自由曲面的面形矢高相同。其中，项自由曲面的加入使其对称轴相对Y轴的旋转角度与Z7项、Z8项系数的关系为

为了进一步展现视场对自由曲面偏振特性的影响，将该离轴系统中的自由曲面去掉，对它进行全视场自由曲面偏振光线追迹，整理各个视场下得到的二向衰减和相位延迟，与之前含自由曲面时得到的数据进行对比，得到各个视场下自由曲面项和Z9项面形引入对二向衰减与相位延迟的最大改变量，如图11 和图12所示。

图11 全视场 项自由曲面对系统偏振像差的影响Fig.11 Effect of freeform with term on polarization aberration in full field of view

图12 全视场的Z9 项自由曲面对系统偏振像差的影响Fig.12 Effect of freeform with Z9 term on polarization ab⁃erration in full field of view

由图11 和图12 可知，无论是中心视场还是边缘视场，偏振像差都受到了不同程度的影响。其中，自由曲面项使二向衰减的最大改变量为0.002 12，相位延迟的最大改变量为0.795°；Z9项使二向衰减的最大改变量为0.000 1，相位延迟的最大改变量为0.036°。

4 视场离轴三反系统的设计及偏振特性分析

为验证上述理论分析结果，本文设计了一个大视场离轴三反光学系统，并对其偏振特性进行分析，流程如图13 所示。

图13 自由曲面偏振光学系统的设计流程Fig.13 Design process of polarization optical system with freeform surface

具体步骤如下：首先，选择适当的光学系统结构，计算该初始结构的基本参数，并进行偏振特性分析：通过动态数据连接机制在Matlab 中编程，读取Zemax 中光学系统的参数。将口径和视场进行等分，然后选取单一视场点，对该视场下的不同光瞳采样点进行偏振光线追迹。当光线入射到自由曲面时，对自由曲面面形进行采样，并采集该光线的入射角，计算光线经过每一个光学元件的琼斯矩阵，最终得到单一视场下所有光线经过光学系统后在出瞳面的琼斯瞳图和三维矩阵，并分别进行泡利分解以及奇异值分解，求出单一视场下该系统的相位像差、二向衰减和相位延迟。切换其他视场采样点，得到全视场下系统的偏振特性分布。根据偏振特性分析结果，通过ZERN 操作数对自由曲面的Zernike 系数进行约束优化，对系统进行公差分析，最后得到理想的光学系统。

为了充分体现自由曲面面形对偏振像差分布的影响，令该系统各元件不含偏心和倾斜，仅利用视场离轴的方法消除系统中心遮拦。系统的光学指标如表1 所示。

表1 自由曲面偏振光学系统的主要光学指标Tab.1 Main optical indicators of freeform polarization op⁃tical system

光学系统的初始结构为三片二次曲面，在初始结构中的反射镜上镀金属膜，波在金属内传播时其波矢量为复数，金属的复折射率表示为n+inκ，其中n和κ为正实数。常见金属对于钠黄光（λ=589.3 nm）的光学常数如表2 所示。其中铝的反射本领随波长的变化比较平稳，它也具有很好的抗腐蚀性，选用铝作为反射镜的镀膜材料［25］。为消除中心遮拦和一次杂光的影响，设计时选取边缘视场成像，不仅会导致成像质量下降，同时也会增加系统的偏振像差。为平衡实际视场中的像差水平，在系统中引入自由曲面，考虑到自由曲面面形对各个视场的影响，会在远离光阑位置的主镜上引入自由曲面。初始结构是一个关于Y轴对称的光学系统，在选取视场和自由曲面时，要注意轴对称的问题，因此，选取自由曲面Z5项对系统进行调制，选取条纹Zernike 多项式Z5项系数为1.753×10−8。仿真结果表明，自由曲面的面形对偏振像差大小有一定的影响，考虑到视场大小为20°×2°，选取中心视场为Y轴上向下偏移8°。经过优化，系统各视场的调制传递函数（Modulation Transfer Func⁃tion，MTF）在38.5 lp/mm 处大于0.6，如图15所示。

表2 金属的光学常数Tab.2 Optical constants of metals

图15 自由曲面偏振光学系统的MTF 曲线Fig.15 MTF curves of freeform polarization optical system

经过全口径自由曲面偏振光线追迹，系统的二向衰减和相位延迟的分布分别如图16 和图18所示。同时，也对系统中自由曲面引起的二向衰减和延迟进行了计算，分别如图17 和图19 所示。设计结果与第3 节的结果一致，不同视场下的二向衰减与相位延迟分布不同，其数值随着视场角的增大而增大。自由曲面所引起的偏振像差占整个系统偏振像差的52.5%。因此，自由曲面的面形会影响系统整体偏振像差的大小和分布，所引起的偏振效应会降低光学系统的成像质量和测量精度。明确自由曲面的面形对偏振像差的具体影响，从系统整体上实现对偏振像差的调制和约束，有助于高精度光学系统的设计优化。

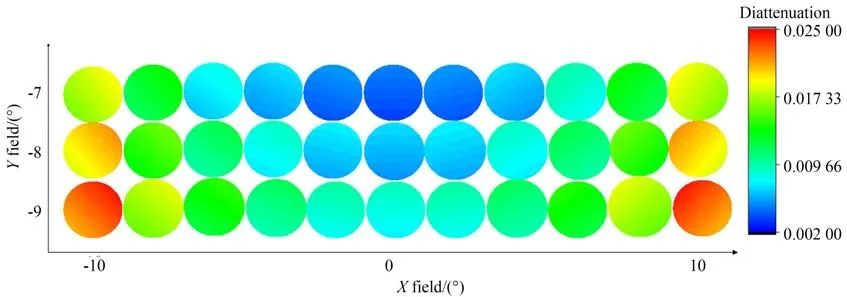
图16 全视场的二向衰减瞳Fig.16 Diattenuation pupil in full field of view

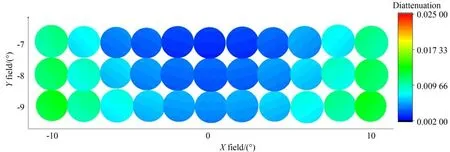
图17 自由曲面的全视场二向衰减瞳Fig.17 Diattenuation pupil of freeform surface in full field of view

图18 全视场的相位延迟瞳Fig.18 Retardance pupil in full field of view

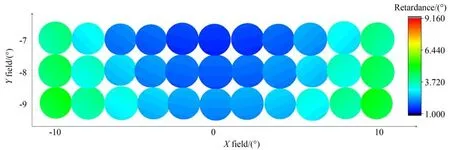
图19 自由曲面的全视场相位延迟Fig.19 Retardance pupil of freeform surface in full field of view

5 结论

为定量分析自由曲面离轴光学系统的偏振像差，本文基于琼斯表示法提出了自由曲面光学系统偏振像差分析方法，构建了离轴自由曲面光学系统的偏振像差解析模型。针对视场离轴的自由曲面单反射系统，获取了全视场下该系统出瞳处的相位像差、二向衰减以及相位延迟像差的分布特性，直观展现了自由曲面对整个系统琼斯瞳的影响。基于自由曲面光学系统偏振分析方法，有针对性地选取Zernike 系数，设计了含有自由曲面的大视场非旋转对称三反光学系统。设计结果表明，自由曲面的引入不仅对波像差有影响，而且不同程度上改变了系统的琼斯瞳分布。目前的研究还仅限于不含偏心和倾斜的自由曲面，为了解析离轴自由曲面光学系统的偏振特性，未来还需进一步分析含偏心和倾斜的自由曲面光学系统的偏振像差分布，从而达到全面指导离轴自由曲面偏振成像光学系统设计的目的。