有限元方法求解二维薛定谔方程

魏健达，张江敏

(福建师范大学物理与能源学院，福建 福州 350117)

现代技术的进步使工程师们需要承接更复杂且昂贵的项目，这些项目非常看重系统的可靠性和安全性．比如：建筑工程、航天飞行、核能开发等，需要技术人员对这些复杂的物理系统建立相应的数学模型用于计算．而自然科学(如热力学、流体力学、固体物理等)总是需要借助偏微分方程[1-3]来对物理系统进行描述，但是往往理论上解析求解一些复杂的偏微分方程是非常困难的，需要借助工具软件做数值仿真．仿真求解最常用的一种方法就是有限元方法[4-5]．有限元一词最早由R.W.Clough提出[6]，现在科学家们普遍认为有限元[7-8]的根源可以追溯到3个独立的研究小组，即应用数学家Courant；物理学家Synge以及工程师Argyris、Kelsey．Taylor的著作The Finite Element Method和麻省理工学院Klaus-Jürgen Bathe教授的著作Finite Element Procedures中均运用有限元方法解决了许多固体力学和流体力学的问题．自 20 世纪 60 年代以来，有限元方法被广泛应用,比如：1973年工程师谢干权和李建华攻克的三维有限元程序应用于对全国大型水坝的计算；在生物力学和手术治疗方面李杰，Deng等[9-10]采用有限元方法研究顶点旋转扳法对颈椎引力的影响，达到减小颈椎间盘应力集中的效果．

在量子力学的一维势阱问题中，人们不会考虑边界对于势阱的影响．但是，当研究二维势阱问题时，就会出现许多不同的边界(比如：圆形边界、椭圆形边界以及本文要用有限元方法仿真的多角形边界)，这些边界对求解的问题的影响是巨大的．本文从二维无限深方势阱出发，用有限元方法去研究不同边界势阱中粒子的本征问题和概率问题，将有限元这种数学中解偏微分方程的方法与量子力学中的问题结合起来，提供了研究量子力学问题的新思路，为进一步探索量子世界开辟新的道路．

有限元方法是把连续的结构离散成有限个单元和有限个节点，再对其组合体进行分析[11-12]，其本质是将大型物理系统细分为更小、更简单的部分．它通过空间维度上特定的空间离散化来实现，将物理系统离散化即可精确表示复杂的几何形状，又可以描述材料特性，从而轻松表示整体解决方案以及精确描述局部的现象．本文利用有限元方法，首先将多角形势阱网格化成矩形单元；然后借助雅可比矩阵转化坐标系，耦合每个矩形单元；最终实现薛定谔方程和概率密度函数的求解．

1 有限元方法

1.1 二维薛定谔方程的弱形式[13]

在二维无限深势阱中薛定谔方程和边界条件表示如下：

(1)

(2)

1.2 物理坐标系与自然坐标系的转换

使用物理坐标系可以直接计算波函数图像，但对于数值计算并不方便．因此，将波函数分割成物理坐标系下规律不明显的四边形小块，再利用形函数[17-19]将物理坐标系中规律不明显的四边形小块(如图1(a))转化成自然坐标系中的矩形单元(图1(b))．

图1 坐标的变换Fig.1 Transformation of coordinates

其物理坐标系的x和y与自然坐标系下的ξ和η之间的转化公式是：

(3)

而ψ对ξ与η的偏导数，可以通过J矩阵和ψ对x与y求偏导数联系起来.

(4)

其中J矩阵可以由形函数推导出来，在本文中称它是联系物理坐标系与自然坐标系的Jacobian矩阵[20-21].

1.3 数值积分多项式

(5)

2 方势阱中的解析解方法与数值方法

2.1 粒子在方势阱中的解析解方法

人们对于求解方势阱问题比较熟悉．其中一个粒子束缚在二维方势阱中的问题，可以通过二维不含时的薛定谔方程[22-24](6)得出．

(6)

其中V在(-a≤x≤a，-a≤y≤a)范围内取值是0，在(-a≤x≤a，-a≤y≤a)范围之外取值是+∞，得到方程的本征波函数和本征值[25-26]分别是：

(7)

图2 基态粒子在方势阱中的概率 密度分布图(解析解)Fig.2 Probability density distribution of ground state particles in square potential well (analytical solution)

2.2 差分方法计算方势阱中粒子的概率密度

差分方法是解微分方程的数值方法，具体而言，是把微分用有限差分代替，把导数用有限差商代替的方法．它将基本方程和边界条件近似的用差分方程表示，将求解微分方程的问题改成求解代数方程的问题．下文用差分方法来求解无限深方势阱中粒子的概率密度．在笛卡尔坐标系中，方势阱的取值范围是(-1≤x≤1，-1≤y≤1)，将图像中x方向和y方向平均分成42份，总共的节点为1 764个．其中取每份的dx=dy=0.048 7．通过解二维方势阱中的薛定谔方程，得到粒子在不同能量下的概率密度分布图，如图3．

图3 不同能量的粒子在方势阱中的概率密度分布图(差分法)Fig.3 Probability density distribution of particles with different energies in square potential well (difference method)

在方势阱中，本文对从差分方法和解析解方法中计算出的能量进行对比．表1可以看出，差分方法有较高的精度，即使到了第三激发态，误差也仅仅为0.4%．

表1 基于方势阱中差分方法与解析解之能量误差Tab.1 Energy errors between the difference method and analytical solution based on square potential well

2.3 网格化对有限元方法精度的影响

划分势阱是有限元方法的核心步骤，选择合理的网格化可以使得有限元方法需要更少的计算却有更高的精确度．将无限深方势阱网格化，以图4为例，取边心距a=1，a被平均截成的Na份(此处取Na=19)，其中每一份的长度da=0.052 6．圆心角2π被平均分成Nθ份(此处取Nθ=40)，其中每一份的度数dθ=0.078 5，见图4．

图4 方势阱的网格化图像Fig.4 Grid image of a square potential well

下文通过对Na和Nθ的改变，来观察何时粒子的能量趋近于稳定，以粒子在方势阱中的基态能量为例．在计算中，令Nθ不变，取Nθ为321，Na从10开始，间隔为5，直至增加到85．网格化图像中的交点也从3 210个开始增加，之后交点的个数分别为4 815，6 420，8 025，9 630，11 235，12 840，14 445，16 050，17 655，19 260，20 865，22 470，25 680，27 285．如图5，当Na开始增加时候，有限元方法解出的基态能量迅速下降，直到Na增加至85，基态能量仍然没有保持稳定．接下去的计算中，令Na不变，并且取Na为40，Nθ从50开始，以20为间隔，直至增加到300．网格化图像的交点从3 240个开始增加，之后交点的个数分别为4 840，6 440，8 040，9 640，11 240，12 840，14 440，16 040，17 640，19 240，20 840，22 440，24 040．如图6，图6中Nθ数量从50开始增加，当数量达到100和150时，计算得到的基态能量不随着Nθ增加而改变精度，当Nθ达到220之后，基态能量保持稳定，基本不随Nθ的变化而变化．

图5 基态能量随log10Na变化关系曲线 Fig.5 Curve of ground state energy

图6 基态能量 随log10Nθ变化关系曲线 Fig.6 Curve of ground state energy

对比图5与图6，有限元方法计算出的基态能量与Na成正相关程度大于其计算出的基态能量与Nθ的正相关程度．Nθ对有限元方法计算基态能量影响较小，Nθ增加了250，数值计算仅仅只改变0.000 607．相比之下Na增加了75，有限元方法的计算基态能量的结果从2.540 365变化为2.048 552，变化量为0.49 1813．

2.4 有限元方法求解粒子在方势阱中的概率密度

本文用有限元方法得出方势阱中基态粒子概率密度分布图(图7)与利用解析解得到的粒子在方势阱中基态粒子概率密度分布图(图2)进行比较．在图7和图2中，可见，当坐标和同时等于0时，z有最大的取值，即方势阱中粒子被测量到的概率最大；随着坐标|x|和|y|的增大，在z方向的数值减小，即方势阱中粒子被测量到的概率减小．

图7 基态粒子在方势阱中的概率 密度分布图(有限元方法)Fig.7 Probability density distribution of ground state particles in square potential well (finite element method)

表2给出了有限元方法和解析解[27-29]的误差分析．由表2可知，从基态到第三激发态，有限元方法与解析解误差保持在4.04%到4.14%之间．有限元方法相对于差分法比较，取大致相同的格点数量，但是它的精度却远远不如差分法来的准确(差分方法与解析解误差保持在0.05%到0.40%)．在对比中可以看见差分方法与有限元方法求得的第一激发态(简并)图像不同，那是因为简并态的波函数是两个“基矢”波函数的叠加，计算机取的系数不同，数值模拟的图像也不相同，这种情况也只会出现在简并态中．但是有限元方法的优点在于它可以解出不同边界的势阱中粒子的概率密度．在图8、图9中，本文利用有限元方法数值计算出了正多角形势阱中不同能量下粒子概率密度．甚至正五角形(非凸)势阱中粒子概率密度分布图(图10)也可以用有限元方法求解．

表2 基于方势阱中有限元方法与解析解之能量误差Tab.2 Energy errors between finite element method and analytical solution based on square potential well

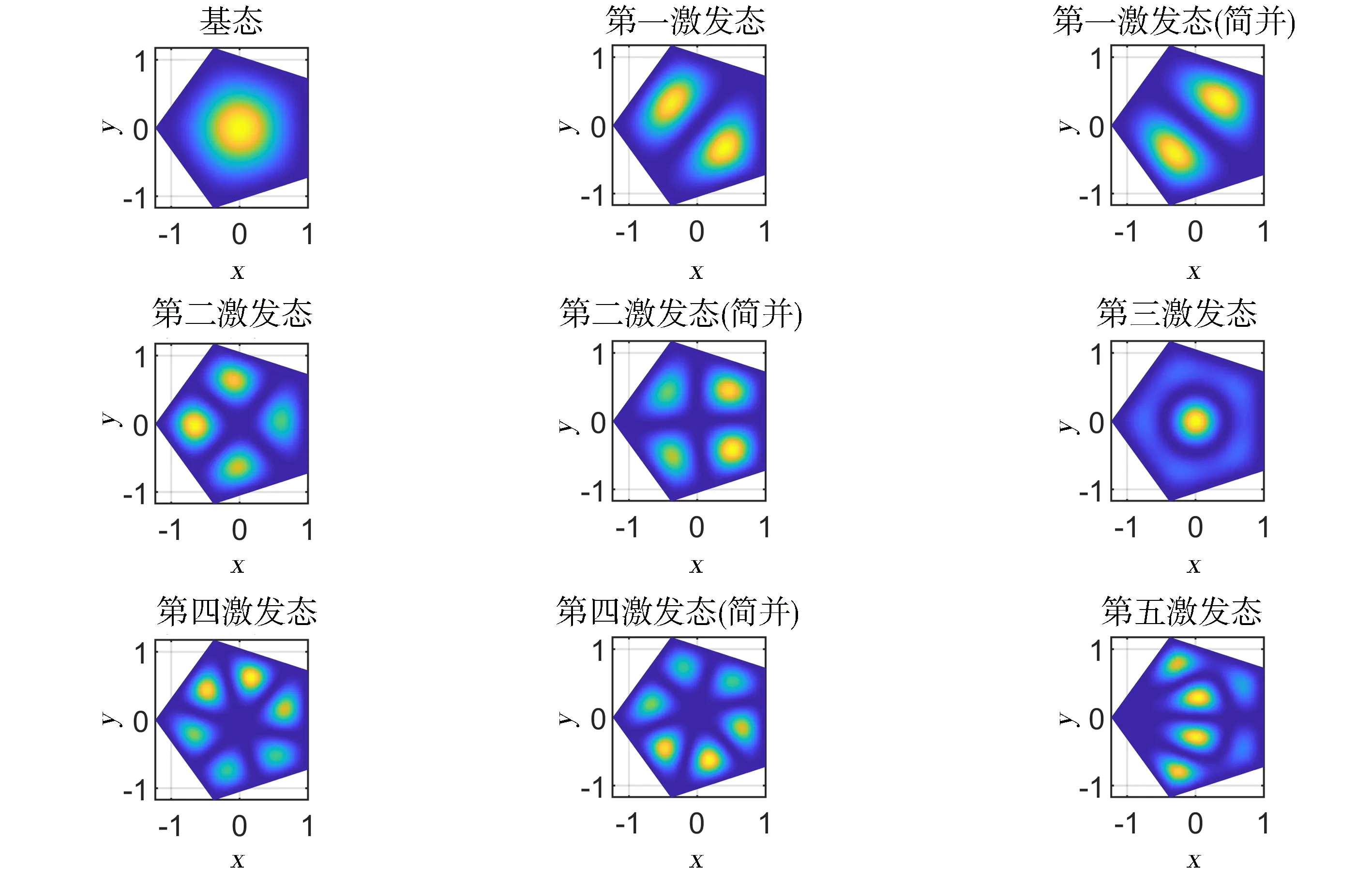
图9 不同能量的粒子在五角形势阱(凸)中的概率密度分布图(有限元方法)Fig.9 Probability density distribution of particles with different energies in pentagonal well (convex) (finite element method)

图10 不同能量的粒子在五角形势阱(非凸)中的概率密度分布图(有限元方法)Fig.10 Probability density distribution of particles with different energies in pentagonal situation well (nonconvex) (finite element method)

3 粒子在多角形势阱中的概率密度

3.1 粒子在正三角形势阱中的解析解

(8)

为了避免方程中粒子的质量与量子数出现混淆，文中将粒子的质量用μ代替，且令a=1．在(8)中m和n只能取大于0的整数，并且在取值上有m≥2n的限制．另外当m=2n时，粒子处于非简并态，例如当m=2，n=1时，粒子在正三角形势阱中处于非简并的基态．粒子在正三角形势阱中波函数为：

(9)

通过用matlab计算，经过平移后，绘制出正三角形势阱中基态粒子解析解图像，如图11所示.

从图11可以看出，当x和y的取值趋近于0的时候，概率密度在z方向上的取值增大．当x=y=0时，概率密度在z方向上有最大值，即粒子在正三角形势阱中出现的概率最大；随着坐标|x|和|y|的增大，在z方向上的数值减小，粒子出现的概率逐渐减小；当到了势阱的边界上时，粒子出现的概率几乎为0．

图11 基态粒子在正三角形势阱中的 概率密度分布图(解析解)Fig.11 Probability density distribution of ground state particles in a positive triangular potential well (analytic solution)

3.2 有限元方法计算粒子在正三角形势阱中的概率密度

有限元方法解得正三角形势阱中基态粒子的概率密度分布图，如图12所示.

图12 基态粒子在正三角形势阱中 的概率密度分布图(有限元方法)Fig.12 Probability density distribution of ground state particles in positive triangular potential well (finite element method)

将有限元方法得出的正三角形势阱中基态粒子的概率密度分布图(图12)与利用解析解得到的粒子在正三角形势阱中基态粒子的概率密度分布图(图11)进行比较．当坐标x和y同时等于0时，两图像在方向都取值最大，即正三角形势阱中粒子被测量到的概率最大；随着坐标|x|和|y|的增大，在z方向的数值减小；当到了势阱的边界上时，粒子出现的概率几乎为0．粒子在正三角形势阱中其他能量下的概率密度分布图见图13．

图13 不同能量的粒子在三角形势阱中的概率密度分布图(有限元方法)Fig.13 Probability density distribution of particles with different energies in triangular potential well (finite element method)

3.3 五角形的网格化方法与有限元方法计算粒子在五角形势阱的概率密度

边界条件对于二维薛定谔方程的解的具体形式有本质的影响，在凸五角形势阱与非凸的五角形势阱中，粒子的概率密度是难以用解析解或者用差分法求解的．但是，有限元计算为这类问题提供了解决办法．以下是本文网格化五角形势阱(凸、非凸)的方式，如图14、图15．

图14 五角形势阱(凸)的网格化图像Fig.14 Grid image of pentagonal well(convex)

图15 五角形势阱(非凸)的网格化图像Fig.15 Grid image of pentagonal (nonconvex) well

在图14中，取边心距a=1，a被平均截成Na份(此处Na=19)，其中每一份的长度da=0.052 6．圆心角2π被平均分成Nθ份(此处Nθ=50)，其中每一份dθ=0.062 8．在图15中，取边心距a=1，a被平均截成Na份(此处Na=19)，其中每一份的长度da=0.052 6．圆心角2π被平均分成Nθ份(此处Nθ=50)，其中每一份dθ=0.062 8．有限元方法计算粒子在五角形势阱(凸、非凸)中基态和激发态的概率密度分布图如图9、图10所示．

4 结束语

本文对不同边界势阱中的粒子概率密度分布图实现了可视化，计算出不同边界势阱中粒子的能量，通过将有限元方法与解析解的对比，证实了有限元方法的可行性，为有限元方法和量子力学的结合提供了重要的实例．与差分方法相比，虽然有限元方法的精度略低，但是它能计算除了方势阱之外的其他边界形貌的势阱，这是非常有价值的．在今后的工作中，将利用有限元方法去处理更多粒子在不同形状势阱中的概率密度问题，以及将这种方法应用到其他量子力学问题．为丰富量子力学研究方法，探索更多有趣且有用的量子现象铺平了道路．