液压伺服激振系统“阀-缸”一体化建模与控制策略设计

张舟钧禹，陈哲吾，戴巨川，胥小强，郭勇

（1.湖南科技大学机电工程学院，湖南湘潭 411201；2.苏州东菱振动试验仪器有限公司，江苏苏州 215000）

0 引言

液压伺服激振系统因其能够提供大动力、准确的激振指标，在各个行业得到广泛应用。然而，作为复杂的机电液耦合系统，液压伺服激振系统运行物理过程、机制十分复杂。现有的研究多集中在系统控制方面，如冯凯等[1]利用遗传算法对采煤机液压系统PID参数优化进行了研究；何常玉等[2]研究了一种基于自适应鲁棒控制策略的液压伺服系统位置控制模式；俞珏等[3]提出了一种基于李雅普诺夫函数的液压系统反馈控制器；许玲玲等[4]设计了一种基于有限滑模控制方法的液压伺服系统控制器；文献[5]～[7]则将模糊控制技术应用于液压伺服系统控制中。这些工作多限于低频段工况，考虑更高频段工况（如地震模拟液压伺服激振台），栾强利等[8]采用了三参量控制技术；崔伟清等[9]提出了速度正反馈的三参量控制技术；李小军等[10]则首次将“加加速度”引入地震模拟台的控制中。

上述研究普遍采用的是伺服阀的简化模型，然而对伺服阀本身的动态特性考虑不足。虽然也有一些文献建立了伺服阀动力学模型，并对其相关结构参数进行了分析或优化[11-13]，或者对伺服阀的运动稳定性和特殊现象（如“啸叫”）进行了研究[14-15]，但基于液压伺服激振系统“阀-缸”一体化模型开展控制特性分析鲜见。基于此，本文建立“阀-缸”一体化的系统模型，在此基础上进一步设计控制策略，并对其控制特性进行分析。

1 液压伺服激振系统组成

图1所示为一种液压伺服激振系统组成。系统进油路上有液压（定量）泵、单向阀、调压用比例阀、高压过滤器、蓄能器、伺服阀、伺服缸等液压元件。其中，液压泵从液压油箱中吸入油液，形成压力油排出，送入下一个执行元件，其本质是将输入的机械能转换成液体压力能。液压泵输出的液压油经单向阀（防止油流反向流动）后作用在比例阀上，其作用是调节系统的工作压力。由于液压伺服阀和液压伺服缸都是敏感的液压件，为了抑制系统内产生或侵入的污染物，在油路中增加了高压过滤器。经过滤后的无污染油液进入伺服阀。伺服阀是带有负反馈的控制阀，可将电信号输入转换为大功率的压力或流量信号输出，亦称为电液转换或功率放大元件。为避免系统高速动作导致系统压力变化过大，安装有蓄能器，对系统起到储能稳压作用。伺服液压缸是终端执行元件，将液压系统产生的动力传递至负载上，获得预期的响应。与普通液压缸相比，伺服液压缸具有抵抗冲击能力强、响应速度快、响应精度高的优点。系统回油路上还安装有背压（溢流）阀，为整个系统提供一定的背压，在管路或设备压力不稳的状态下，保持管路所需压力。如图1所示，该液压伺服系统中安装有阀位移传感器、台位移传感器和台加速度传感器。这些传感器实时动态测量系统的工作状态并反馈回测量控制单元，经计算后输出伺服阀的控制信号，调节伺服阀的输出流量。与此同时，测量控制单元同步将测量、控制信息传输至上位机监控系统。

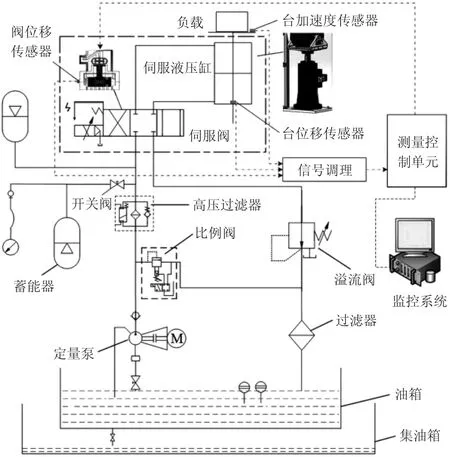
图1 电液伺服激振系统原理图

设计液压伺服系统的根本目的是根据负载的需求提供系统动力和运动。在液压伺服阀和液压伺服缸特性一定的条件下，关键在于构建出其系统模型并获得其控制特性。

2 液压伺服激振系统建模

2.1 伺服阀建模

2.1.1 基本原理

图2（a）所示为一种伺服阀结构，在无控制信号时，衔铁由弹簧管支撑在磁体的中间位置，滑阀阀芯处于中位，伺服阀处于关闭状态。当有控制信号输入（差动电流Δi）时，衔铁上产生电磁力矩，带动射流管产生小角度的偏转，引起滑阀工作腔两端产生压差，推动滑阀阀芯移动，从而达到控制进入液压缸工作腔的压差（PA-PB），使液压缸产生运动。

2.1.2 衔铁射流管组件运动方程

射流管组件由衔铁、控制线圈、弹簧管等原件组成（图2（b））。控制信号（差动电流Δi）通过线圈使得磁铁磁体组件产生磁通，从而使衔铁上产生电磁力矩，带动衔铁中心绕弹簧管中心发生一定的偏转角度。

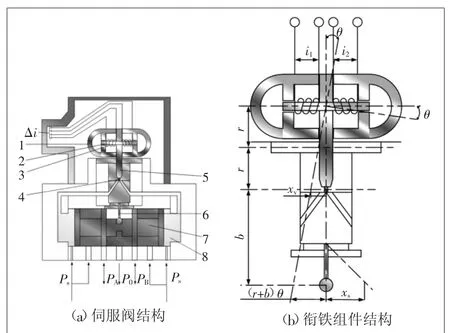
图2 伺服阀及其衔铁组件结构原理图

在电磁力矩的作用下，衔铁组件的运动方程组可表达为[16]：

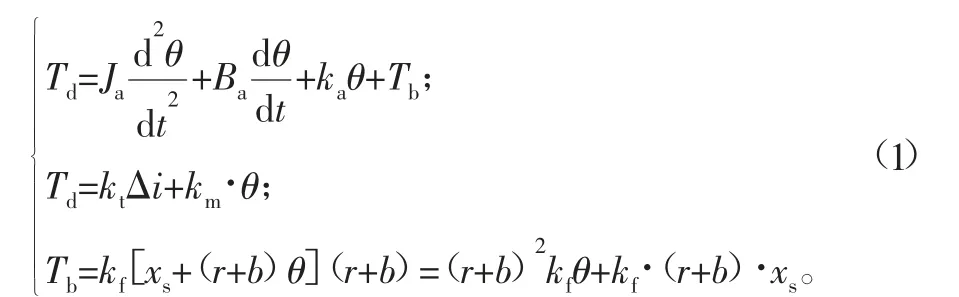
式中：Td为衔铁上的电磁力矩；Tb为反馈弹簧对衔铁组件产生的力矩；Ja为衔铁组件转动惯量；θ为弹簧偏转角度；Ba为衔铁组件阻尼；ka为弹簧管刚度；kt为电磁力矩系数；km为力矩马达中位弹簧刚度；kf为反馈弹簧刚度；r为射流管中心至弹簧管回转中心距离；b为反馈杆中心至射流管中心距离；xs为阀芯位移。

根据式（1），可以进一步得到

在图2（b）中，由于偏转角θ一般很小，故其转动位移xv和θ的关系在复数域可表示为

据此可得输入信号Δi伺服阀阀芯位移xs的传递模型如图3所示。

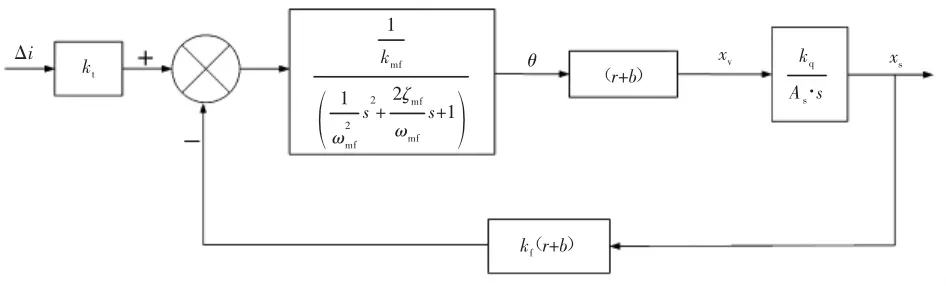
图3 伺服阀传递函数模型

2.2“阀-缸”一体化建模

图4（a）所示是某伺服液压缸外形图（带测试件），其原理如图4（b）所示；伺服液压缸安装有位移传感器及加速度传感器。控制系统根据伺服液压缸实际输出位移信号或加速度信号与相应控制信号的偏差值，经调理后作为伺服阀的控制信号，调节伺服阀中射流管的偏转角度，从而改变作用在滑阀两端的压力与流量，进而达到控制液压缸运动状态的目的。由此可见，伺服阀和液压缸之间具有密切的耦合效应。因而采用“阀-缸”一体化建模能更好地反映其行为特性。

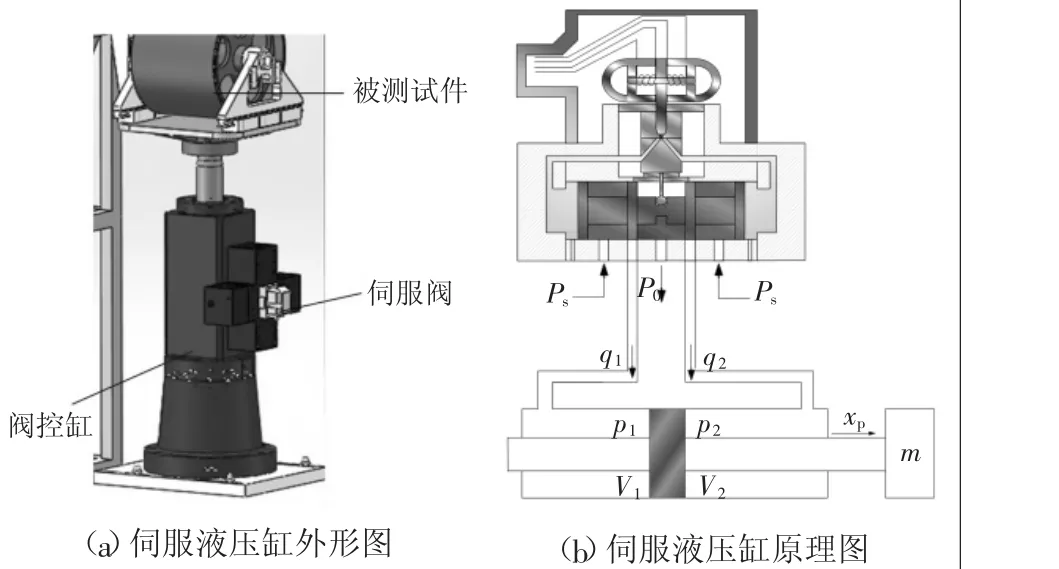
图4 某伺服液压缸外形与原理图

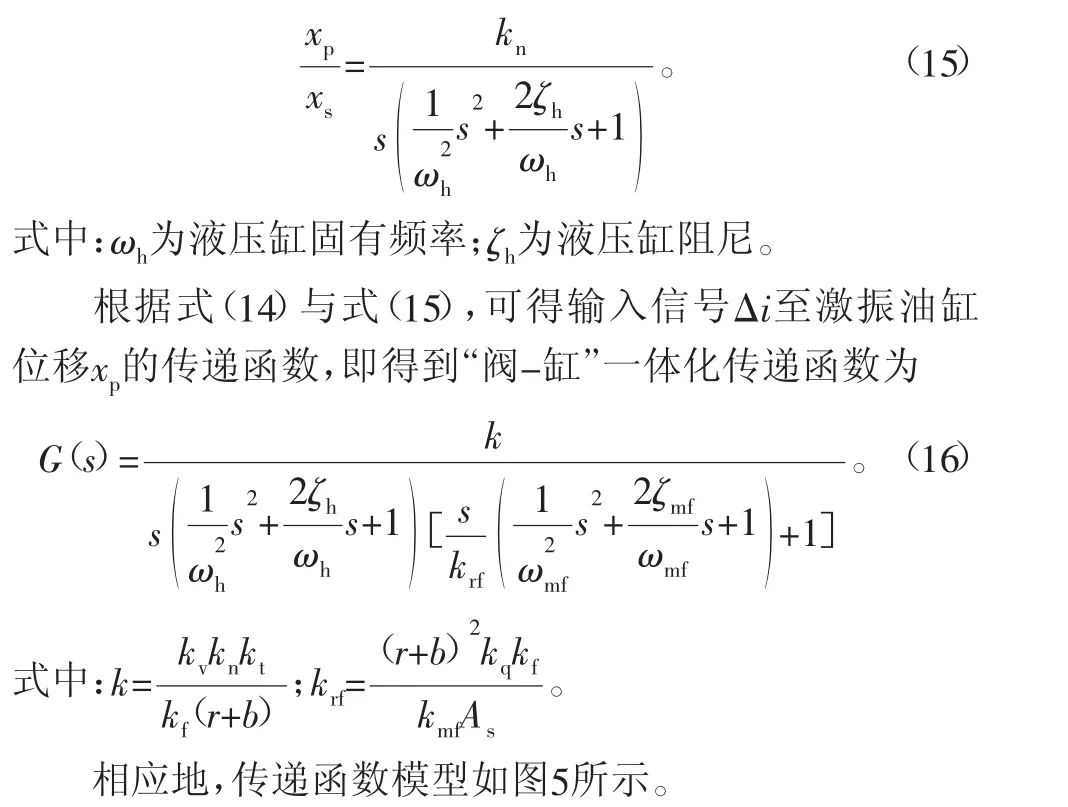
对于液压缸的建模，国内外已经有大量的研究，故详细过程不在此处讨论。根据文献[17]，伺服阀位移xs至液压缸活塞位移xp的传递函数可表示为

3 系统控制策略设计

3.1 控制策略的确定

液压伺服激振系统控制策略对其性能具有至关重要的影响。本文在综合分析现有文献控制策略的基础上，结合三状态控制[8]和四状态控制[10]的优点，设计了一种混合控制策略如图6所示。该控制策略的特点是在输入端引入了前馈环节B（s），从输出端引回反馈环节D（s），其表达式为：

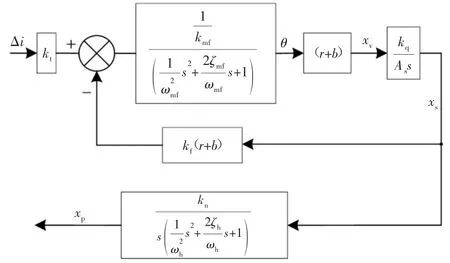
图5 “阀-缸”一体化模型

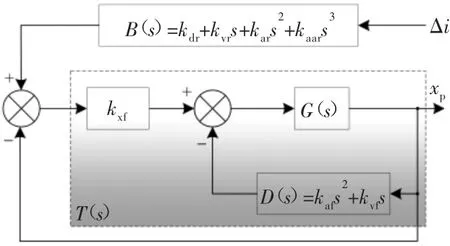
图6 混合控制策略框图

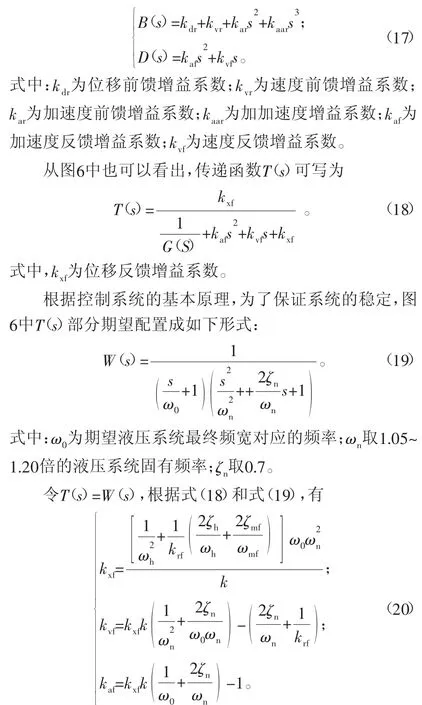
此外，前馈控制器的作用是对消反馈补偿后系统中制约频宽的靠近虚轴的极点，以达到拓展系统频宽及提高系统跟踪性能的目的。基于该原理，前馈控制器应满足如下条件[18]：

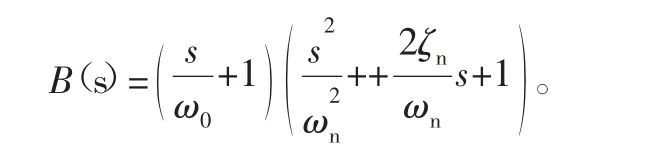
整理可得

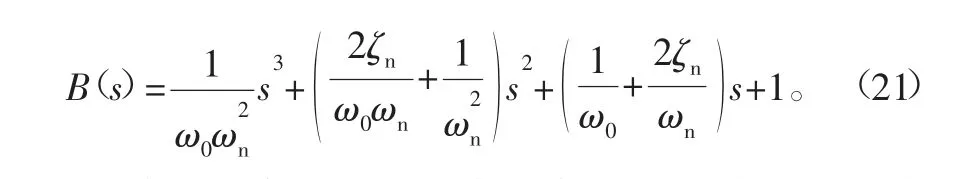
根据式（17）中B（s）表达式和式（21），可得到如下参数表达式：

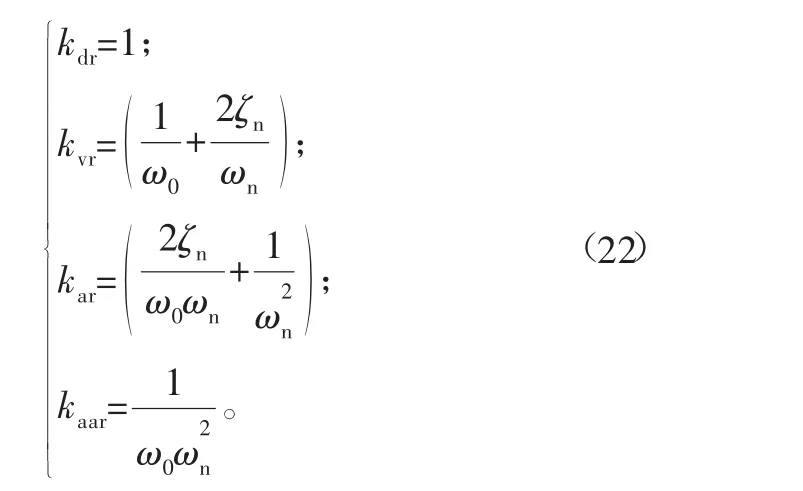
基于前述分析， 在Matlab/Simulink 环境中搭建系统仿真模型，系统主要参数如表1所示。仿真时，以电流信号作为指令信号输入，液压缸工作台面位移输出为跟踪信号。图7（a）、（b）、（c）分别给出了控制信号频率为2 Hz、5 Hz、10 Hz，设定指令幅值均为5 mm时系统输出（跟踪）信号仿真结果。

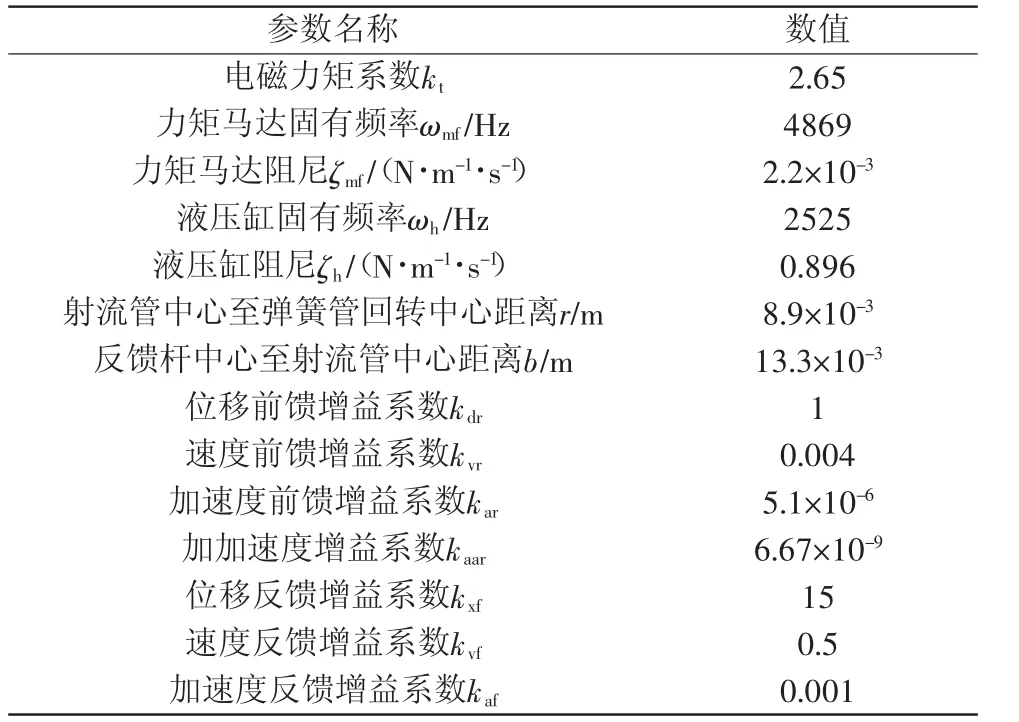
表1 仿真参数

从图7（a）可以看出，在控制信号为2 Hz正弦激励信号时，输出信号与期望跟踪信号基本一致，控制精度较高，但在仿真初始0～0.2 s的时间段内，输出信号存在一定扰动。在图7（b）中，输入信号提高为5 Hz正弦激励信号，输出信号与期望跟踪信号整体上重合度仍然较好，但在初始阶段有较明显的扰动，同时控制精度有所下降。进一步采用10 Hz的控制信号（如图7（c）），仿真开始阶段输出信号的扰动比5 Hz时更为显著，而且扰动持续的时间也更长，控制误差也更明显。根据上述分析不难判断，随着控制信号频率的增加，输出扰动剧烈程度不断增加，控制精度也会逐步降低。

3.2 控制参数的修正

为了使控制系统能适应多个频率的激振需求，本节基于模糊理论，将位移反馈系数进行模糊化，使其能随系统输入信号变化而在规定的模糊论域根据模糊规则变化，从而更好地对液压系统进行调节。设计的模糊控制器输入为跟踪位置误差E（期望跟踪信号与实际跟踪信号之差），以及E 的变化率EC。也就是说，位移反馈系数修正以误差E及E的变化率EC作为输入，通过模糊控制对位移反馈系数进行修改，以满足不同时刻对位移反馈系数整定的要求。这里，设置E的基本论域为[-6，6]，EC的基本论域为[-3，3]，其中模糊语言采用的变量值为负大NB、负小NS、正大PB、正小PS、0位Z。设计的参数模糊规则表如表2所示，响应面如图8所示。

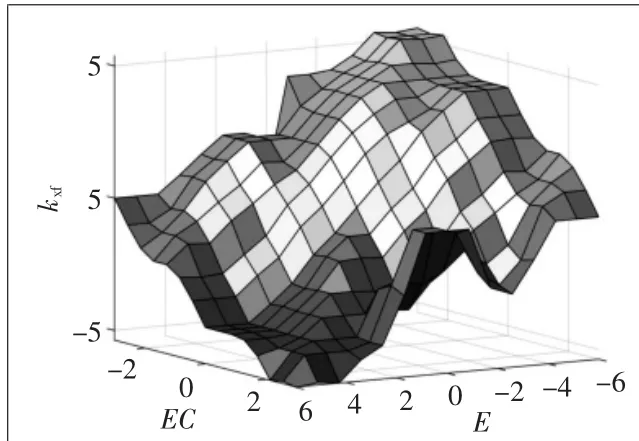
图8 模糊规则响应面

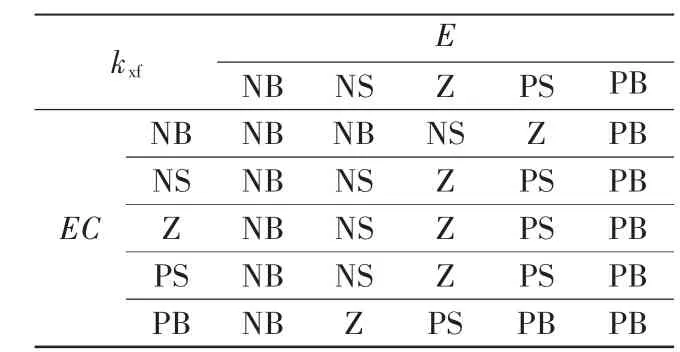
表2 模糊规则表

系统仿真仍采用表1中数据，输入控制信号分别为2 Hz、5 Hz、10 Hz正弦激励信号，经仿真后得到结果如图9所示。图9（a）为控制信号2 Hz时参数修正之后的结果。与图7（a）中的结果相比，其初始阶段的振荡明显消除。由于低频段控制精度较好，参数修正前后控制精度变化并不明显。图9（b）为控制信号5 Hz时，参数修正之后的结果。与图7（b）中的结果相比，可以发现输出信号初始扰动仍然明显消除。从控制精度方面来看，其效果也进一步优于未修正前的结果。当控制信号为10 Hz时，对比图7（c）与图9（c）的结果可知：参数修正之前的结果存在很强的初始扰动，参数修正后不但有效消除了信号初始扰动，且较大幅度提高了系统的精度。由此可见，采用模糊方法修正参数，可有效抑制系统输出扰动，同时在一定程度上提高控制精度。需要说明的是，参数修正后会加大实际跟踪信号与期望跟踪信号之间的相位差。

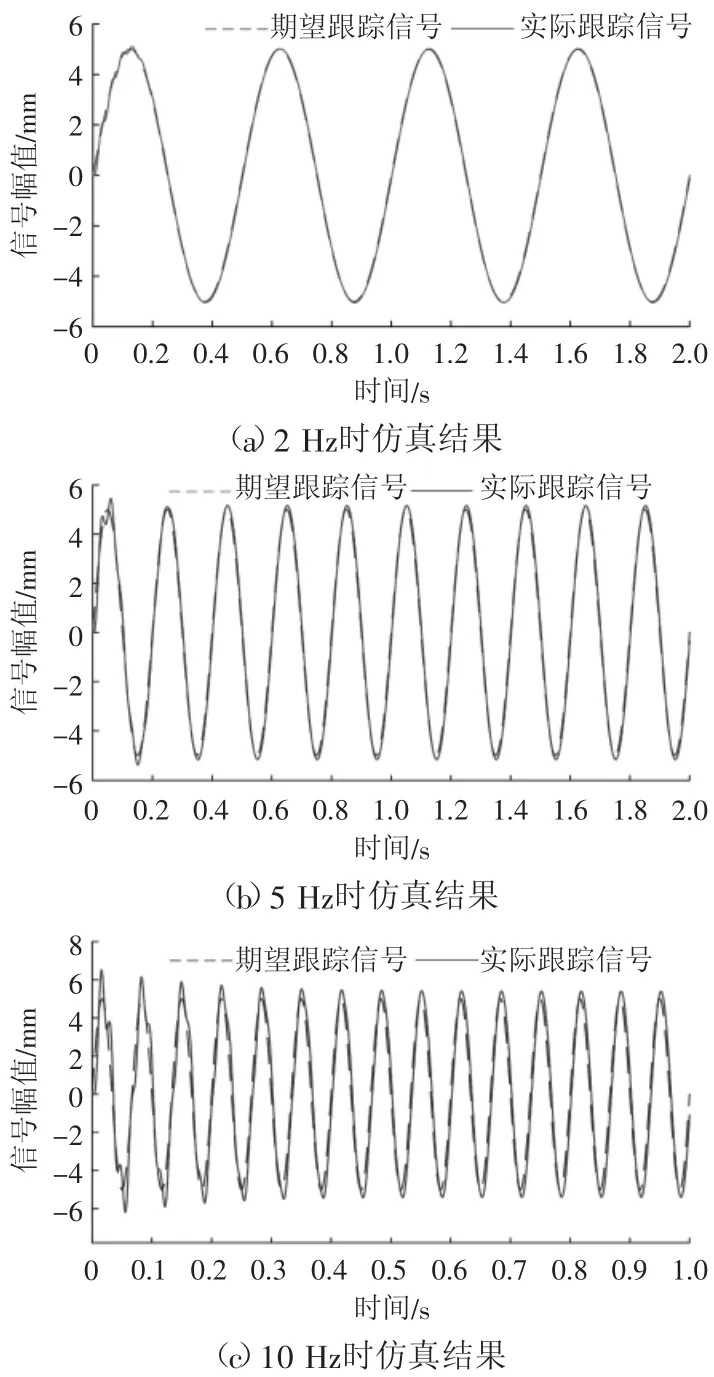
图7 系统跟踪信号仿真结果

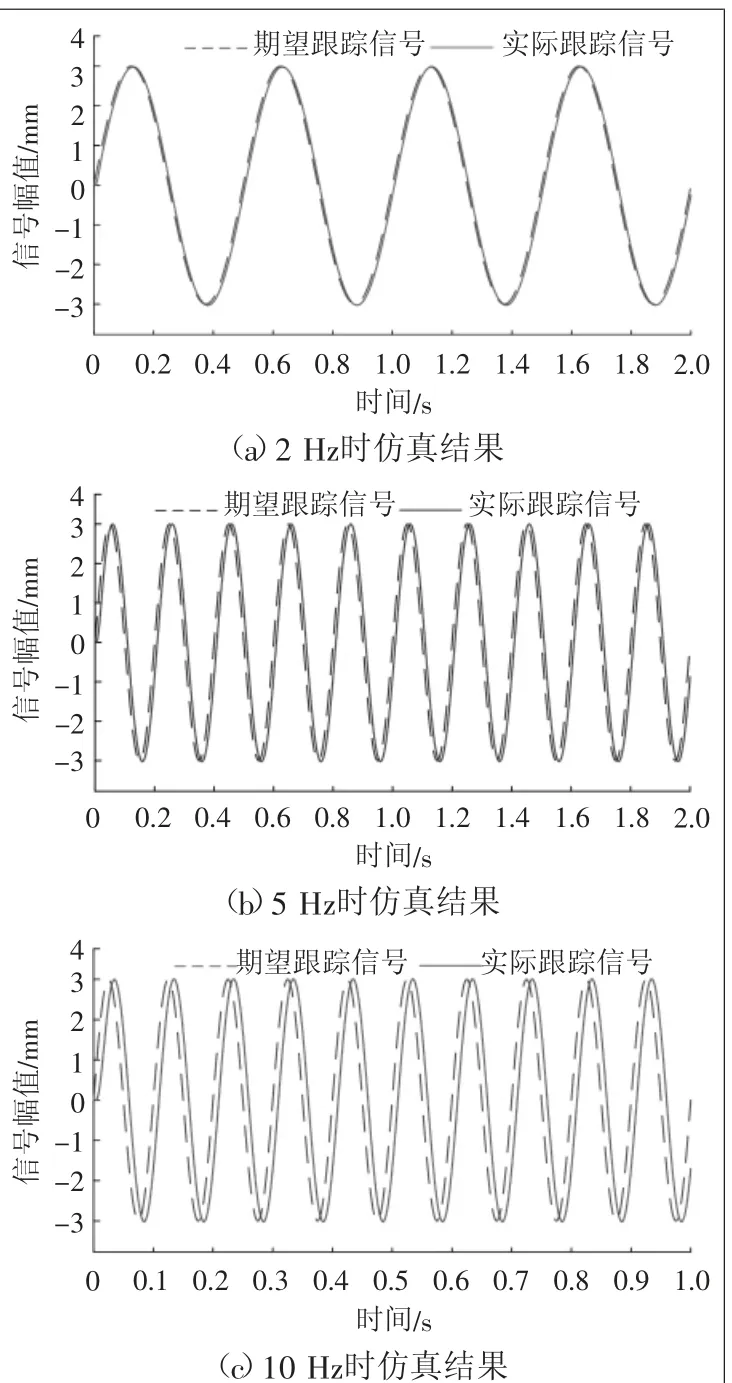
图9 系统跟踪信号仿真结果（参数修正后）

4 结论

针对现有液压伺服激振系统研究中对伺服阀本身动态特性考虑不足、系统控制性能有待提高的问题，开展了“阀-缸”一体化模型构建与控制特性研究。从衔铁射流管组件运动方程出发，详细推导并建立了伺服阀输入信号至阀芯位移的传递函数模型，并将伺服阀模型与液压缸模型结合，得到“阀-缸”一体化模型。设计了一种由三状态反馈与四状态前馈相结合的混合控制模型，并基于模糊理论完成了控制参数的修正。结果表明：设计的混合控制模型能够实现液压伺服激振系统的有效控制。采用模糊方法修正参数，可有效抑制系统输出扰动，同时在一定程度上提高控制精度；参数修正后会加大实际跟踪信号与期望跟踪信号之间的相位差。