基于课程思政的数学分析课程教学设计探讨
陈立宇,王伟芳
基于课程思政的数学分析课程教学设计探讨
陈立宇,王伟芳
(唐山师范学院 数学与计算科学学院,河北 唐山 063000)
“立德树人”是教育的根本任务,如何在教育的过程中处理好知识传授和价值引领的关系,做好“课程思政”,真正提高人才培养的质量,是值得每一位教师思考的问题。本文以数学分析课程为例,探讨如何在数学分析课程的教学中融入思政元素。
课程思政;价值引领;数学思维;创新意识
高校教师不仅承担着传授专业知识的重任,更要培养学生正确的三观,塑造学生健全的人格。“培养什么人,为谁培养人,如何培养人”是每位高校教师首先要回答的问题。育人工作不只是通过学生工作和思政课程来实现,更应充分挖掘专业课程的思政功能,将思政元素与专业课有机融合在一起,通过专业课程教学实现对学生潜移默化的积极影响。数学分析是数学与应用数学、信息与计算科学等专业的基础课程,是一门理论体系完备、内容丰富、应用十分广泛的课程,该课程的教学质量和学习效果直接影响到学生对专业的学习兴趣和未来的职业规划,通过该门课程的学习,学生可进一步掌握数学知识、培养数学思维、提升数学素养。由于数学类专业学习难度大、要求高,需要学生具备克服困难的精神、严谨的学习态度和科学的数学思维,这些素养则需要通过专业基础课程的教学来培养。
本着“能融则融、宜融则融”的原则,精心设计教学,重视知识目标和能力目标,更要融入情感态度与价值观的教学目标,在授课过程中,潜移默化地开展思想引领,更好地服务于学生的成长、成才。
1 发挥价值引领作用,培养民族自信和科学的精神
1.1 家国情怀的培养
在引入反常积分时,引例第二宇宙速度问题归结为无穷积分问题,说明国家的航天事业需要我们这样具有专业知识的人才,激励学生们努力学好专业知识,练就为国家做贡献的过硬本领。通过简要介绍从毛主席提出要搞人造卫星到我国成为第五个独立发射人造卫星的国家这一段历史,培养学生的家国情怀。
1.2 民族自信的培养
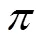
2 提升认识高度,培养学生的哲学思维
2.1 一般与特殊的关系

都存在且相等。
海涅定理是德国数学家海涅(Heine)给出的,它建立了数列极限和函数极限的桥梁,而数列极限是特殊的函数极限,利用海涅定理可以将数列极限转化为函数极限,即可以通过一般的函数的极限来求特殊的数列的极限。
2.2 整体与部分的关系
数列与子列极限的关系充分体现了整体与部分的关系。

数列及其子列的上述关系深刻揭示了变量变化的整体与部分之间的关系[3]。
2.3 普遍联系的观点
不定积分和定积分是分别定义的,微积分学基本定理将这两个看似不相干的概念联系了起来,并揭示了它们之间的内在联系。
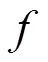
类似的,反常积分和无穷级数是两个不同的概念,而积分判别法也将两者联系起来。数学分析中类似的体现普遍联系观点的结论还有很多。
2.4 量变与质变的观点
在极限定义的形成过程中,经历了三个阶段:
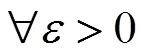
每一次质的飞跃都是量变的积累,是量变达到一定程度的必然结果。任何事物的发展都是量变与质变的辩证统一,数学分析的发展也不例外。
3 优化教学过程,培养学生的数学思想
3.1 化归转化思想
不定积分作为非构造性定义,其定义并未给出不定积分的求法,因此求不定积分问题最终都归结为将被积函数变形为基本积分表中不定积分的类型,如何转化,就需要学生掌握化归转化思想,如
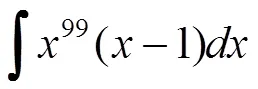
两个不定积分,被积函数均为单项式与多项式的乘积,但前者直接乘开即可,后者则因为多项式项数过多而不好表示。
在教学过程中,通过精心设计例题,对例题归类,启发学生思考,在掌握了
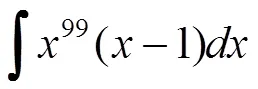
的求法后,分析用同样的方法求
3.2 数形结合思想
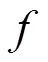

如图1所示,罗尔中值定理的几何意义是满足定理条件的曲线上必有一点处的切线平行于轴,接下来启发学生思考,如果将曲线的右端点上移至如图2位置,那么可以得到什么结论?

图2 拉格朗日中值定理的几何意义
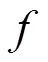
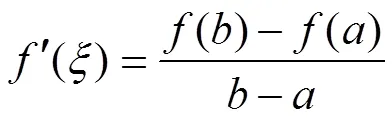
在给出拉格朗日中值定理后,进一步引导学生思考:如果曲线由参数方程给出,拉格朗日中值定理的结论又是怎样的呢?这样就引出了柯西中值定理。
3.3 反例思想
多元函数可微的必要条件指出:可微必连续,可微必可偏导,但反之不一定成立,反例怎么举?
根据可微的必要条件,不可偏导一定不可微,因此,在找连续不可微的反例时,就可以找连续且偏导数不存在的函数,而函数

在教学过程中,通过启发式教学法,引导学生找出反例,从而更好地理解和掌握结论。
3.4 类比思想
数学分析中四次出现阿贝尔和狄利克雷判别法,定理的条件都有相似之处。在教学过程中,提醒学生进行类比归纳,启发学生自主构建知识的网络。
4 创新教学方法,培养学生的团队协作意识和创新精神
4.1 学以致用的意识
在讲授条件极值时,可以先提出一个问题:易拉罐为什么要这么设计?然后分析如果将易拉罐分别设计成长方体和圆柱体,怎么设计用料最省?通过探索让学生明白易拉罐这样设计的原因,理解如何通过数学建模为企业节约成本,增强学生的节约意识和环保意识[7]。
4.2 团队协作意识
在讲授一元函数最值时,已知闭区间上连续函数的最值的求法,若把闭区间换作开区间,最值该如何去求?采用小组讨论法,课前发布讨论任务,分小组讨论,课上各小组充分发言,最后教师点评、总结、补充、提炼。通过参与式、互动式教学,充分调动学生的学习积极性,培养学生的团结协作意识。
4.3 创新意识
在讲授反常积分的阿贝尔狄利克雷判别法时,采用启发式教学,由柯西收敛准则和积分第二中值定理推导出两个定理的条件[5],在还原定理的发现过程,培养学生的创新意识和思维能力。
[1] 孙玉芹,刘建军.有限的生命与无限的价值——“数列的极限”教学案例[J].教育教学论坛.2019(42):175.
[2] 华东师范大学数学系.数学分析(第4版上册)[M].北京:高等教育出版社,2010:54.
[3] 李文林.数学史概论(第3版)[M].北京:高等教育出版社, 2011:79-84.
[4] 华东师范大学数学系.数学分析(第4版下册)[M].北京:高等教育出版社,2010:118-125.
[5] 反常积分的阿贝尔和狄利克雷判别法教学初探[J].唐山师范学院学报.2016(2):27-29.
[6] 朱国卫.以海涅定理为例谈数学分析中的证明,直觉和感悟[J].吉林省教育学院学报,2010,26(7):154.
[7] 数学分析“课程思政”的实践与思考[J].创新教育研究, 2019,7(5):675-678.
The Teaching Design of Mathematics Analysis Course Based on Ideological and Political Education Through Curricula
CHEN Li-yu, WANG Wei-fang
(School of Mathematics and Computational Sciences, Tangshan Normal University, Tangshan 063000, China)
“Moral education” is the fundamental task of education. How to deal with the relationship between knowledge imparting and value leading in the process of education, achieve “ideological and political education through curricula”, and really improve the quality of talent training are worth thinking. Taking the course of mathematical analysis as an example, how to integrate ideological and political elements into the teaching of mathematical analysis is analyzed.
ideological and political education through curricula; value leading; mathematical thinking; innovation consciousness
O171
A
1009-9115(2021)06-0112-04
10.3969/j.issn.1009-9115.2021.06.026
2020-12-08
2021-07-06
陈立宇(1990-),男,河北唐山人,博士,讲师,研究方向为流体仿真模拟。
王伟芳(1984-),女,河北定州人,硕士,讲师,研究方向为基础数学。
(责任编辑、校对:赵光峰)

