带单机器人的流水作业排序问题的复杂性

时 凌，张 琼，龙彩燕

（广州工商学院通识教育学院，广东 广州 510850）

0 引言

带单机器人的流水作业排序问题可描述为：给定m台机器M1，M2，…，Mm和n个工件J1，J2，…，Jn，每个工件Jj在m台机器的工序为Qi,j(i=1,2,...,m;j=1,2,...,n)，其加工顺序为：Q1,j→Q2,j→...→Qm,j.工序Qi,j在机器Mi上的加工时间为pi,j，且在加工时不可中断.每台机器在同一时间只能加工一个工件，而每个工件在同一时间只能在一台机器上加工.笔者假设同一工件在一台机器上完工后到下一台机器加工之前存在一定的运输时间tj,k，所有的运输工作均由单机器人R来完成，且单机器人R同时只能运输一个工件，于是在机器人R和机器Mi之间就会出现一定的冲突.假设所有的加工时间pi,j和运输时间tj,k均为正整数.

1 排序问题F2,R1| p1,j=p2,j=pj;tj∈{T1,T2}|Cmax 的复杂性

由于排序问题F3||C存在同顺序最优解［8］，所以该排序问题只考虑同顺序的最优解.用σ和τ分别表示工件在机器M1和M2上的加工顺序，C(σ,τ)表示排序问题的最小完工时间.

引理1［2］对于加工时间和运输时间分别为pi,j、tj的排序问题则：

其中，σ-1(k)和τ-1(k)分别表示工件Jk在序列σ和τ中的相应位置.

定理1排序问题是强NP-困难的.

证明利用强NP-困难的3-划分问题［9］到排序问题的归约来证明该排序问题也是强NP-困难的.

3-划分问题：给定正整数集X={x1,x2,...,x3m}和正整数b，且满足

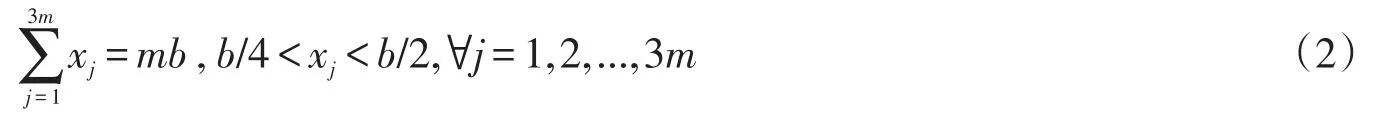
确定整数集X是否存在包含3个元素的m个不相交的子集{X1,X2,...,Xm}的划分，且

给定3-划分问题的一个实例，定义具有下面2类工件的排序问题

（1）3m划分工件，或者称为P-工件：

（2）m大工件，或者称为L-工件：

门槛值为y=3mb+3b，相应的确定性问题为：是否存在完工时间C(S)不超过门槛值y=3mb+3b的加工顺序S.

假设3-划分问题的解存在，设 {X1,X2,...,Xm}是满足式（3）的划分，其中，Xi=(xξ(i),xη(i),xς(i))(i=1,2,...,m).

对于每个工件Jj构建包含工件ξ(j),η(j),ς(j)和工件 3m+j，其加工顺序为 ((3m+1);ξ(1),η(1),ς(1);(3m+2);ξ(2),η(2),ς(2);...;(4m-1);ξ(m),η(m),ς(m);4m)，如图1 所示.

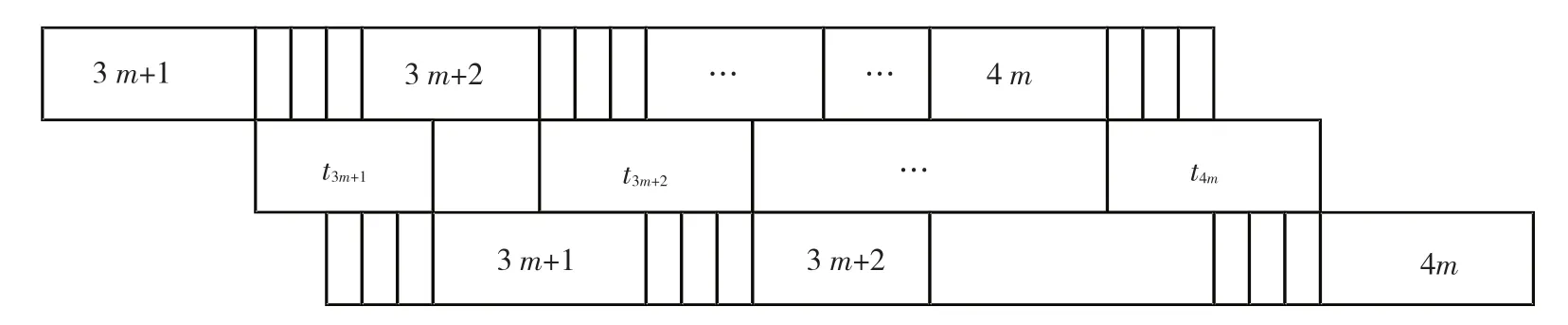
图1 排序问题F2,R1| p1,j=p2,j=pj;tj∈{T1,T2}|Cmax的甘特图Fig.1 Gantt chart for the F2,R1| p1,j=p2,j=pj;tj∈{T1,T2}|Cmaxscheduling problem

则对于图1给出的加工顺序S，显然满足：C(S)≤y.

于是得到同顺序的S且C(S)=y，且有如下结论：

（1）因为p1,j＞0，先加工工件(3m+1)；

（2）因为p2,j＞0（j≠m），工件4m安排在最后加工；

（3）机器M1在区间［0,3mb］内加工工件，且无空闲时间；

（4）机器M2在区间［3b,3mb+3b］内加工工件，且无空闲时间；

（5）单机器人R在区间[(3i+2)b,(3i+4)b](i=0,1,...,(m-1))内运输工件，且无空闲时间.

不失一般性，假设机器以{1,2,...,m-1,m}的顺序加工工件，即按单调递增的顺序加工工件.设工件(3m+1)与工件(3m+2)之间加工的工件子集为X1={i1,i2,...,ik}，如图2所示.

图2 排序问题F2,R1| p1,j=p2,j=pj;tj∈{T1,T2}|Cmax的子图Fig.2 Subgraph for theF2,R1| p1,j=p2,j=pj;tj∈{T1,T2}|Cmaxscheduling problem

于是X1≠Φ，否则在工件(3m+1)和工件(3m+2)出现空闲时间，与结论（3）～（5）矛盾.下面证明k=3和成立.假设表示工件Jj按加工顺序σ在机器Mi上的完工时间，则：

如果k≤2，则有：

如果k≥4，则有：

另一方面，由于工件(3m+1)必须先完成运输才能加工，因此工件(3m+2)不会在时间2b+kb之前在机器M加工.于是工件(3m+1)在机器M完工时间为，但工件(3m+2)在机器M1上还没有完成集合X1中工件的加工，与结论（4）矛盾，故必须有k=3.这就意味着单机器人R在时间段[2b,3b]和时间段[3b,4b]运输工件 (3m+1)和工件 (3m+2).所以，即：

另外，由于机器M2在时间段[4b,6b]没有空闲时间，因此工件(3m+1)在机器M2上的完工时间不迟于6b，则有：

因为p1,i=p2,i=xi，所以

即X1是包含3个元素且满足

同理可证余下的集合X2,X3,...,Xm也是满足包含3个元素且满足故集合X1,X2,...,Xm就是包含3元素且满足的3-划分问题的解.

证毕.

2 小结