大视场角入射平行平面板像差分析方法

曹一青, 沈志娟

(1. 莆田学院 机电与信息工程学院, 福建 莆田 351100; 2. 福建省激光精密加工工程技术研究中心, 福建 莆田 351100)

平行平面板是由两个平行折射平面组成的光学元件, 常用于工作性能较高的光学仪器设计中, 如滤光片和补偿平板等, 在光学系统光程计算中, 反射棱镜可等效为平行平面板. 目前, 对平行平面板特性的研究已引起人们广泛关注[1-2]. 随着图像传感器的快速发展, 大视场角入射光学系统已广泛应用于安全监控和机器人导航等领域中, 该类光学系统中通常包含平行平面板, 虽然平行平面板像差对系统成像影响较小, 但人们对系统成像分辨率要求较高, 因此需减小平行平面板产生的像差.

物点发出的光束经大视场角入射平行平面板后, 在子午和弧矢平面内的聚焦位置不同, 波阵面形状严重偏离球面, 它具有平面对称光学系统的成像特性[3], 使得用于轴对称光学系统像差分析的Seidel像差理论不再适用于该类光学系统的成像分析[4-5].

目前对平面对称光学系统的研究方法较多, 主要有光程差函数法[6-7]、 解析点列图法[8-9]、 李变换法[10]和波像差方法[11-12]. 由于多元件光学系统总波像差为系统中各光学面波像差线性相加, 因此用波像差方法研究系统像差的表达式较简单. 文献[13-14]用波像差方法研究了平面对称光学系统, 提出了三阶像差理论, 并将其扩展到折射系统中. 目前对于平行平面板的像差特性分析和设计大多聚焦于近轴入射光学系统[4,15-16], 在大视场角入射下, 仅依赖于光学设计软件Zemax或CODE V[17-18]进行分析. 基于此, 本文用平面对称光学折射光学系统的三阶像差理论研究大视场角入射平行平面板像差计算方法. 首先, 研究多个平行折射平面的像差分析方法, 推导出相应的计算表达式； 其次, 推导出单个平行平面板的波像差和像差系数； 最后, 分别用像差计算表达式和光学设计软件Zemax计算两个光学系统的像差. 结果表明, 本文的像差表达式正确.

1 大视场角入射光学系统的定义

大视场角入射光学系统具有平面对称光学系统成像特性, 由于视场角范围较大, 若将视场角作为变量, 则像差级数不收敛, 因此其像差分析方法为： 在视场范围内, 先选取几个特定视场角, 再用平面对称光学系统三阶像差理论对其进行计算, 通过得到的各视场角像差综合评判系统成像[19]. 综上所述, 对于大视场角入射平行平面板, 仅需研究各视场角物点的像差特性, 图1为由单个光学面组成的平面折射光学系统光路[14,19-20], 其中O0oO1为基光线,S0为基光线上的一个物点；S0PS1为S0发出的任意一条孔径光线, 与光学元件表面相交于点P；χηz′为光学元件表面的坐标系, 由于在超大视场光学系统中仅需研究基光线物点的成像, 因此光瞳中心P′点与光学元件表面中心o点重合, 从而使光瞳坐标系xyz与χηz′坐标系重合；n0和n1分别为光学元件的物方空间和像方空间的折射率；α和β分别为基光线的入射角和反射角/折射角.

图1 单个光学面组成的平面对称折射光学系统光路Fig.1 Optical path of plane symmetrical refractive optical system composed of single optical surface

在光学元件表面顶点坐标系χηz′中, 平面对称光学元件的面形方程式[3]为

(1)

根据三阶像差理论, 仅需将式(1)进行Taylor级数展开到四阶,

z=c2,0χ2+c0,2η2+c3,0χ3+c1,2χη2+c4,0χ4+c0,4η4+c2,2χ2η2,

(2)

其中

(3)

R和ρ分别为超环面的主半径和次半径.

2 多个平行折射平面光学系统三阶像差

平行平面板由两个平行折射面组成, 若光线以较大角度入射在光学平面上, 则其具有平面对称光学系统成像特性.这种情形下仅需研究主光线像差, 即不考虑关于视场角的像差系数项.若将式(2)中主半径R和次半径ρ均设置为无穷大, 则该光学面为平面.因此, 在原有的平面对称光学系统三阶像差理论基础上推导出单个折射平面的物方四阶波像差系数, 其表达式为

单个光学折射平面的波像差计算表达式[14]为

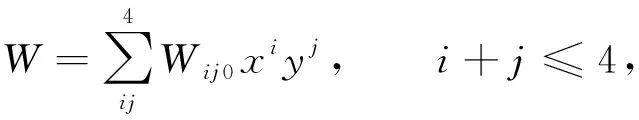
(12)

式(12)中的波像差系数Wij0表达式为

(13)

且

(14)

其中n0/1=n0/n1.

图2 双光学折射平面大视场角入射主光线的传输示意图Fig.2 Schematic diagram of transmission main ray of large field of view incident with birefringence plane

应用二阶波像差w200=0和w020=0的条件, 求解光学面的物方和像方的子午和弧矢焦距[19-20]为

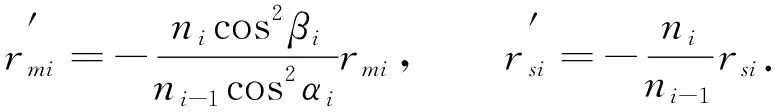
(18)

(19)

根据上述讨论, 第i个光学面的像差由剩余的三阶和四阶波像差决定,

(20)

对于多个光学折射平面的系统, 总的波像差为

(21)

其中

(22)

式(22)中

(23)

(24)

其中像差系数dij0和hij0的表达式分别为

3 单个平行平面板像差表达式

单个平行平面板的光路如图3所示, 由两个光学折射平面组成的平行平面板波像差[3]为

图3 单个平行平面板的光路Fig.3 Optical path of single plane-parallel plate

结合式(22)和(23), 波像差表达式(34)可变换为

其中

(36)

应用式(13)和传输方程式(15)～(18), 可得式(35)中波像差系数Wij0(1)和Wij0(2)的表达式为

4 数值验证

为验证大视场角入射平行平面板像差计算表达式的正确性, 参考文献[19]给出的系统像平面上像差计算流程图, 在MATLAB软件平台上, 应用推导出的像差表达式计算两个含平行平面板的大视场角入射光学系统像差, 并与光学设计软件Zemax得到的结果进行对比分析. 光学系统Ⅰ包含两个平行平面板, 在此基础上, 设计了另一个光学系统Ⅱ, 即在平行平面板后面加入一组双胶合透镜. 光学系统Ⅰ和Ⅱ的光学结构参数分别列于表1和表2, 其对应的入瞳直径分别为5,4 mm； 对应的系统光路分别如图4和图5所示.

表1 光学系统Ⅰ的光学结构参数

在工作波长为587.56 nm的D光入射下, 由本文推导出的像差表达式和光学设计软件Zemax分别计算得到的光学系统Ⅰ和光学系统Ⅱ的像差点列分别如图6和图7所示, 其中(A)和(B)分别为光学设计软件Zemax和本文像差表达式得到的结果, 在3个不同视场情形下对应的像平面位置分别为159.90,96.59,15.64 mm处的像差点列图, 视场角标注在图的右上方. 在像差计算过程中, 所有视场角的物点与系统第一个光学面之间沿主光线的距离均设定为300 mm.

表2 光学系统Ⅱ的光学结构参数

由图6和图7可见, 像差表达式与光学设计软件Zemax计算得到的点列分布图形状和尺寸大小结果相符, 表明像差表达式具有较高的计算精度, 从而验证了本文研究方法的有效性, 但二者存在微小差异, 这是由于更高阶的像差(包括本征像差和衍生像差)影响所致. 对于光学系统Ⅰ, 每个视场角物点发出的平行光束经两块平行平面板后出射的光束也是平行的, 在像平面上的像差分布主要取决于光束宽度, 使得在3个不同视场角0°,30°,60°的结果较接近.

综上, 本文在平面对称光学系统三阶像差理论的基础上, 提出了一种大视场角入射的平行平面板像差分析方法, 推导出相应像差计算表达式, 并结合含平行平面板的光学系统实例, 应用光学设计软件Zemax对其进行像差计算, 将结果与本文推导的像差计算表达式计算结果进行对比分析. 结果表明, 用像差表达式计算的结果精度较高. 本文研究的大视场角入射平行平面板像差解析分析方法为其成像分析提供了一种有效方法, 有助于系统优化设计.