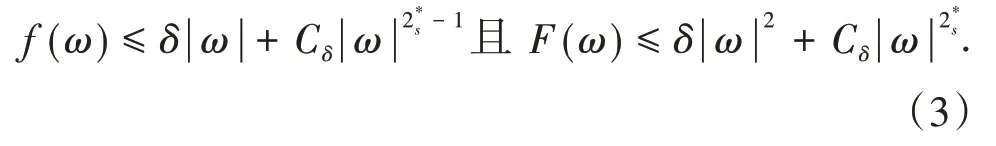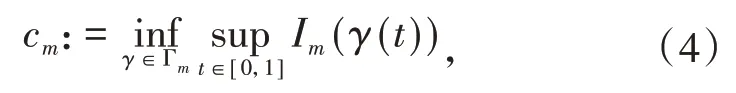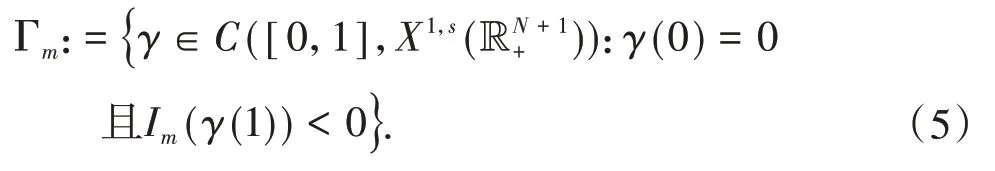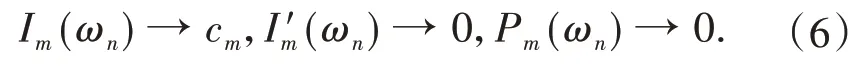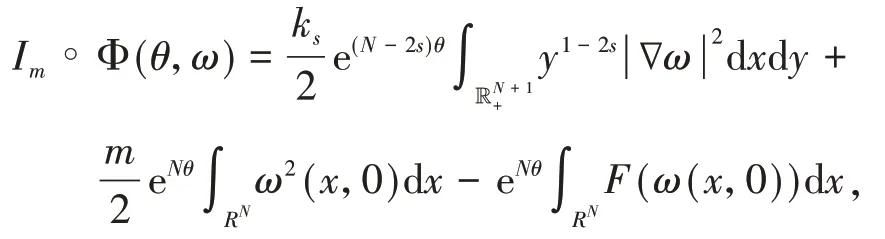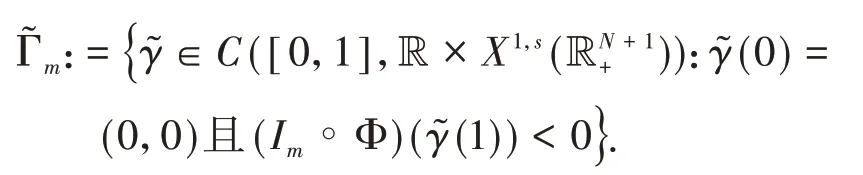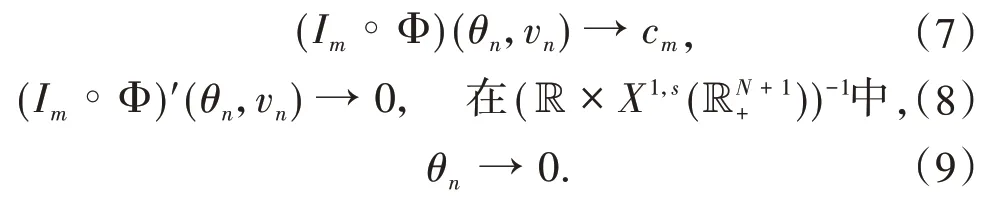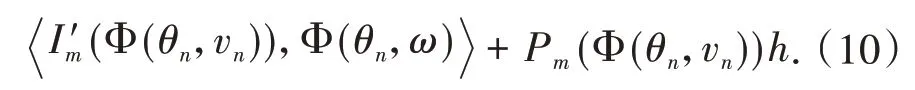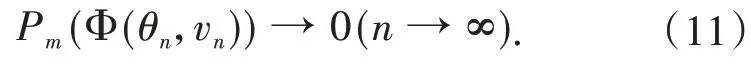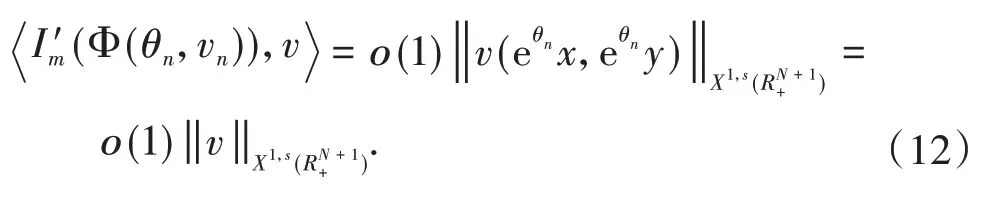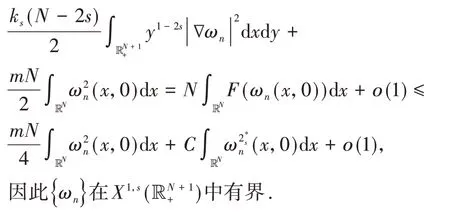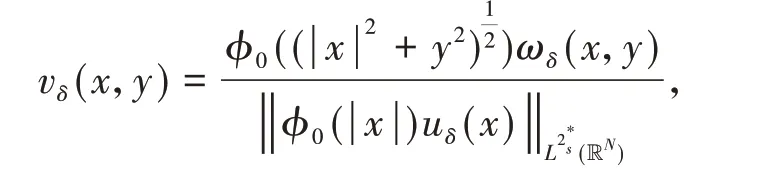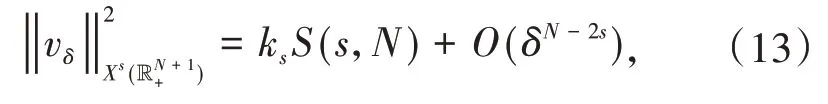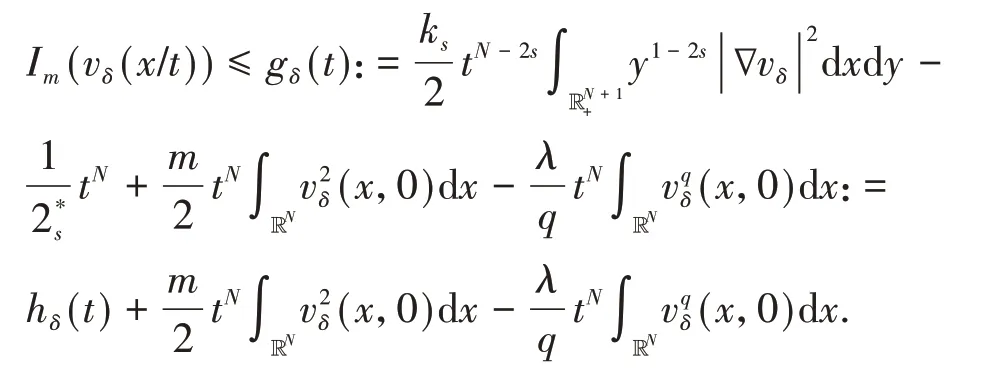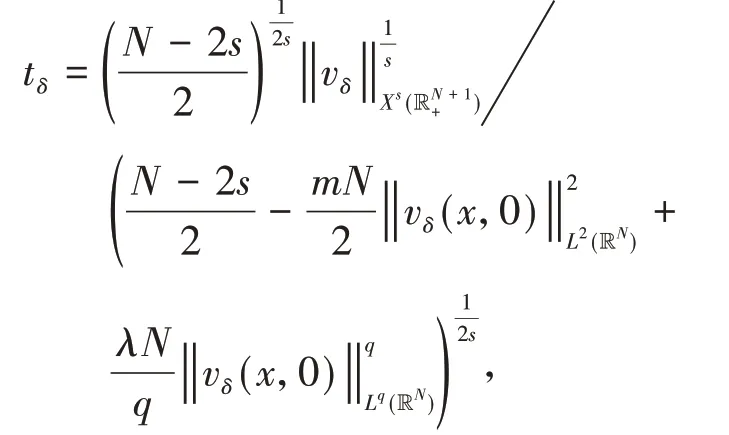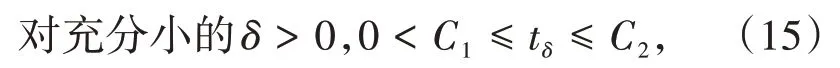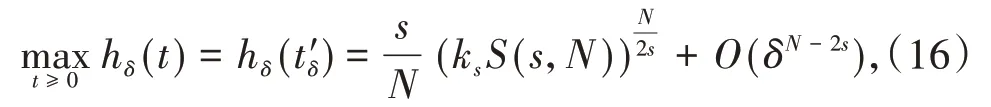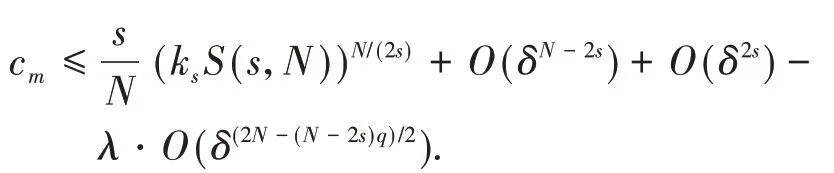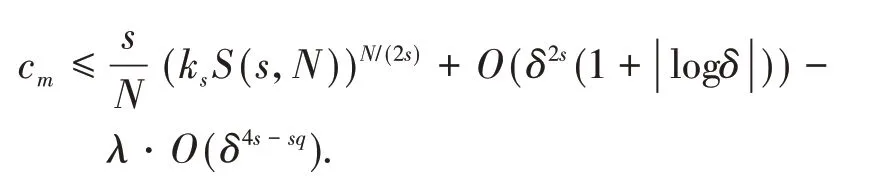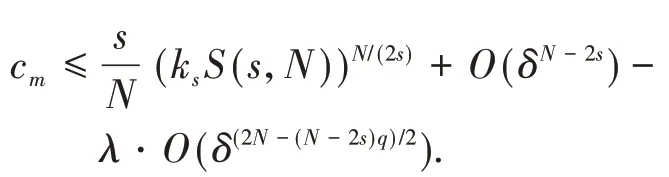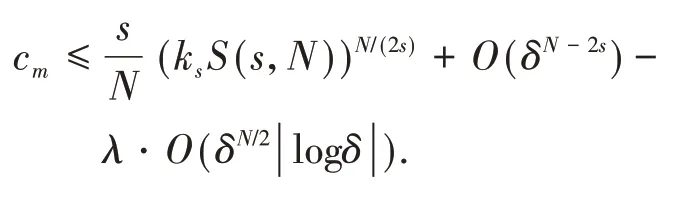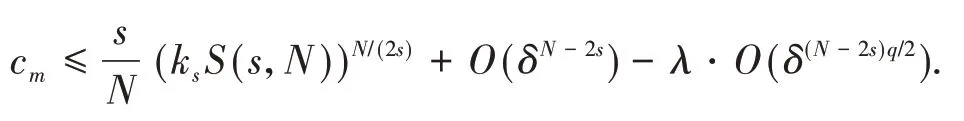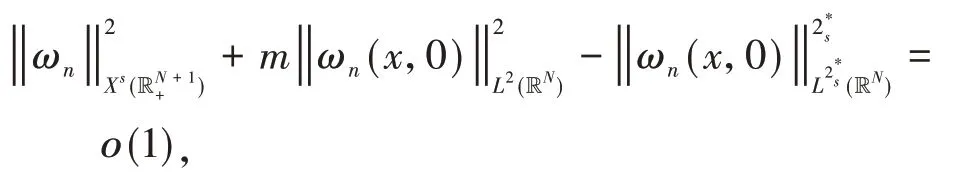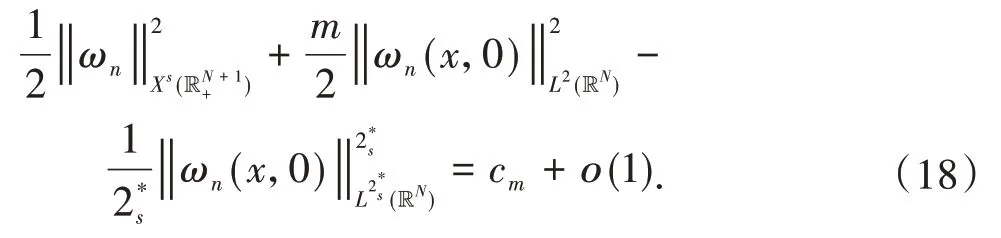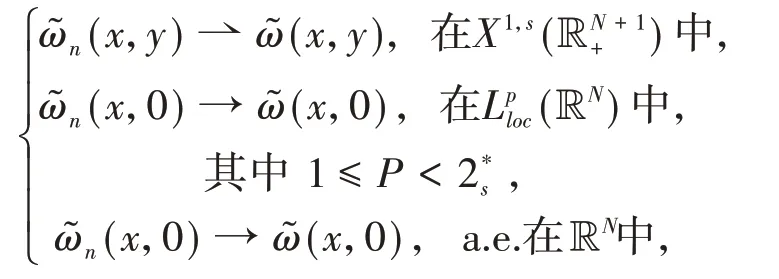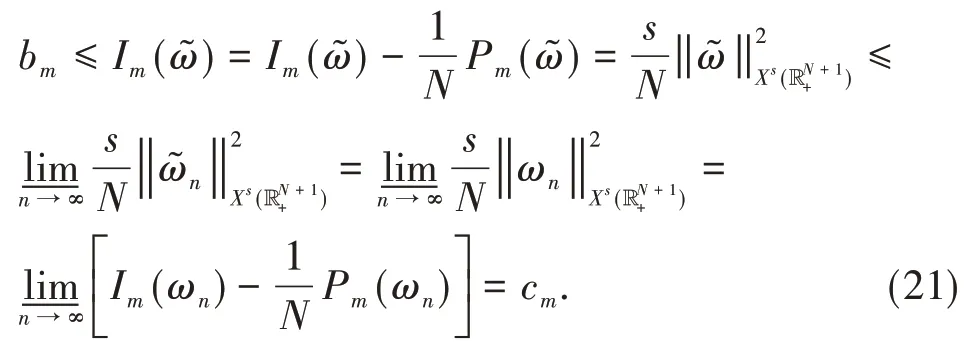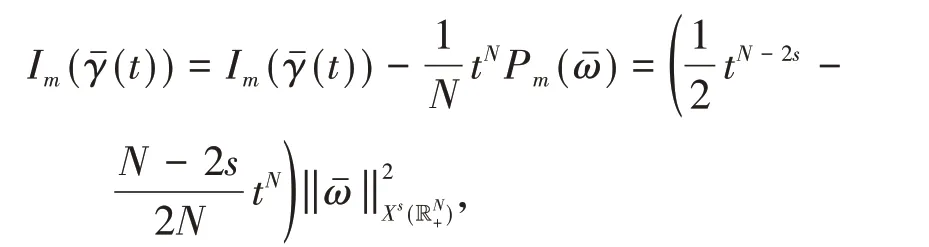带有一般非线性项的分数阶薛定谔方程基态解的存在性

何毅，陈梦若，杨占英

（中南民族大学 数学与统计学学院，武汉 430074）

1 相关介绍

考虑以下分数阶薛定谔方程：

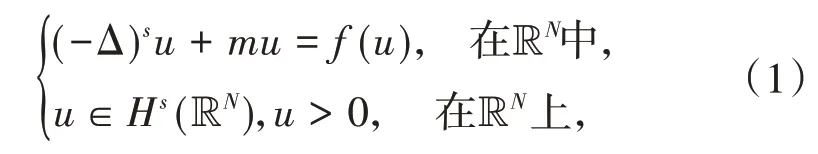
其中m>0，N>2s，(-Δ)s，s∈(0，1)是分数阶拉普拉斯算子，f：R→R是连续函数.为了找到正解，假设当t<0时，f(t)=0.此外，需要以下条件：

注意到，对于s=1的情形，条件（f1）-（f3）最早是由文献［1］引入的.这些假设可以看作是由著名的Berestycki-Lions型条件［2-3］到具有临界增长的分数阶薛定谔方程的推广.

方程（1）是许多物理现象的模型，例如相变、守恒定律，特别是分数阶量子力学等［4］.方程（1）由文献［5-6］提出，是经典非线性薛定谔方程s=1的推广，其中量子路径的布朗运动被Levy扩散过程替代.更多的物理背景参考文献［7］.

近年来，分数阶薛定谔方程的研究吸引了众多数学家的广泛关注.文献［8-10］研究了分数阶薛定谔方程的自由边界问题，得到了一些正则性估计.文献［11-12］研究了全空间中分数阶薛定谔方程解的存在性、唯一性、对称性、正则性、极大值原理和定性性质.

注意到在条件（f1）~（f3）下，没有关于分数阶薛定谔方程正基态解存在性的结果.

为了处理非局部问题（1），本文利用文献［13］的延拓方法研究相应的延拓问题：

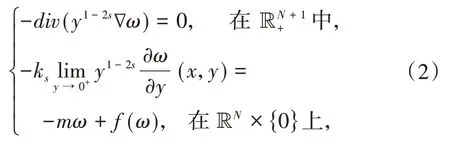
对应的泛函为：

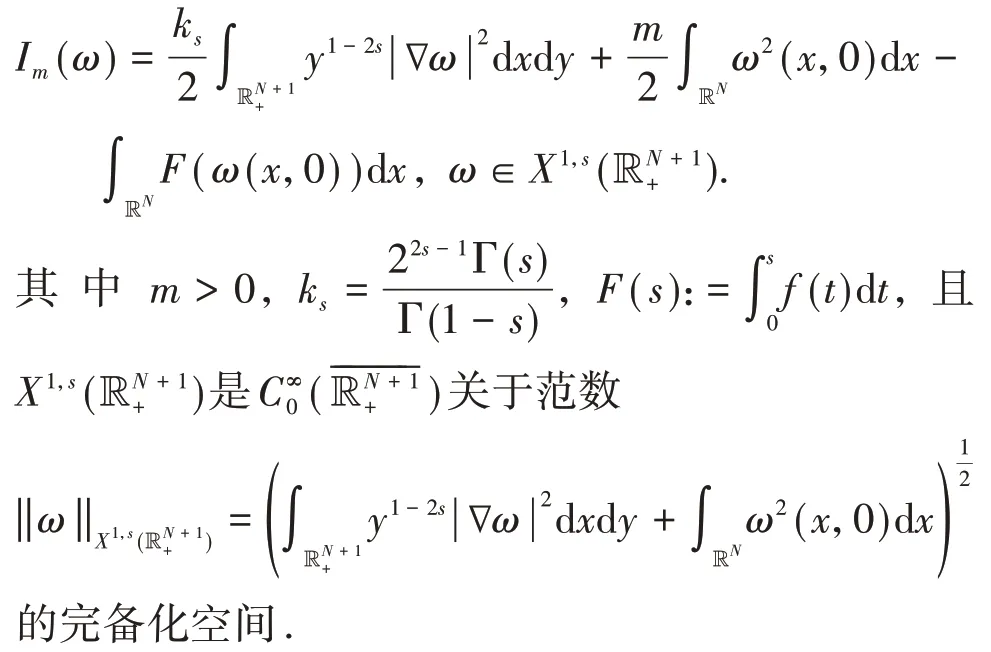
受文献［14］的启发，将一般极小极大原理（文献［15］的定理2.8）应用于复合泛函：

构造有界的(PS)cm序列且当n→∞时，有Pm(ωn)→0，其中cm是泛函Im的山路值，并且Pm(ω)=0是方程（2）的Pohozaev恒等式.运用标准的集中紧的讨论，得到方程（2）基态解的存在性.

2 预备知识

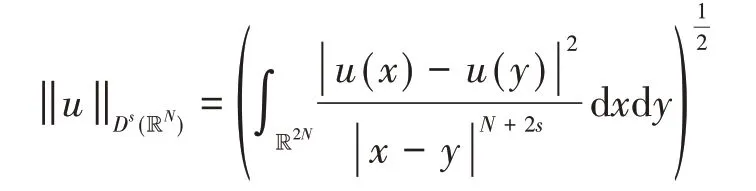
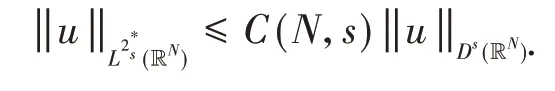
分数阶Sobolev空间Hs(RN)定义为：

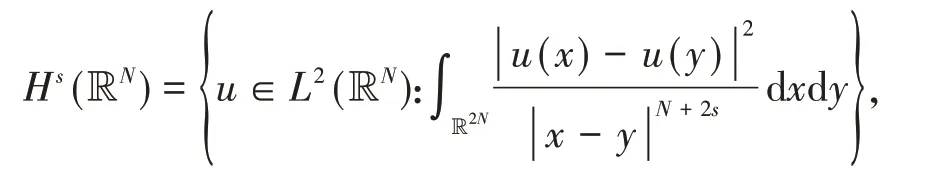
对于N>2s，从文献［17］的引理1可以知道：对于连续地嵌入到Lp(RN)中.

算子(-Δ)s(00}中通过Dirichlet-Neumann映射将方程（1）转化为一个局部问题.对于u∈Ds(RN)，问题

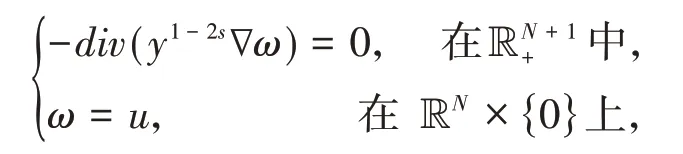
的解ω∈X()称为u的s-调和扩张，记为ω=Es(u).s-调和扩张和分数阶拉普拉斯算子关于Poisson核有明确的表达式：

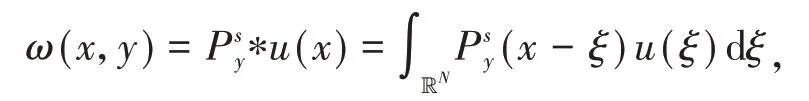
定 义Xs(RN+1+)是关 于 范 数的完备化空间.由文献［19］知，映射Es(⋅)是Ds(RN)和Xs()之间的等距映射，即对ω=Es(u)，有：

另一方面，对于函数ω∈Xs()，将它在RN×{0}上 的迹记 为u(x)：=Tr(ω)=ω(x，0)，并 且迹算 子满足：

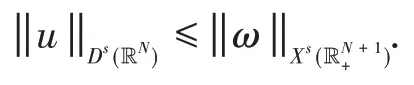
以下的引理1源引自文献［19］定理2.1.

引理1对任意的ω∈Xs()，有成立，其中u：=Tr(ω).最 佳 常 数 取 精 确 值S(s，N)=，并且对于δ>0和ωδ=Es(uδ)，当uδ(x)=δ(N-2s)2(|x|2+δ2)-(N-2s)2时，S(s，N)可以达到.

3 主要结果及其证明

由文献［20-21］可知，如果ω∈X1，s()是方程（2）的弱解，则下面的Pohozaev恒等式成立：

本文的主要结果是：

定理1假设非线性函数f满足条件（f1）-（f3）.如果或者2s0，方程（1）有正的基态解.此外，对于充分大的λ>0，如果2s

在证明定理1之前，先给出几个引理：

引理2Im具有山路定理的几何结构，即：

（i）存在ρ0，α0>0，使得对所有的

（ii）存在ω0∈X1，s()，使得Im(ω0)<0.

证明（i）由条件（f1）和（f2）可知，对∀δ>0，∃Cδ>0，使得：

在（3）式 中 取δ=m4，从 引 理1中 得 到：然后令ρ0，α0>0充分小，（i）成立；

（ii）对R>0，T>0，定义：

因此定义Im的山路值为：

其中：

由引理2的（i），得到cm>0.此外，记：

{0}是方程(2)的非平凡解}.

接下来，将为能量值趋于cm的泛函Im构造（PS）序列，使其满足当n→∞时，Pm(ωn)→0.

命题1存在中的序列使得当n→∞时，

证明定义映射以及(x，y)∈对任意泛函Im° Φ为：

其中：

在文献［15］定理2.8中设ε=εn：=1/n2，δ=δn：=1/n，则可知（7）式、（8）式是文献［15］定理2.8（a）和（c）的直接结论.由（4）式和（5）式，对于ε=εn：=1/n2，存在γn∈Γm，使得：

对任意的(h，ω)∈R×X1，s()，有：(Im° Φ)′(θn，vn)，(h，ω)=

在（10）式中取h=1，ω=0，有：

对任意v∈X1，s()，设（10）式中的ω(x，y)=v(eθnx，eθny)，h=0，由（9）式得到：

在（7）式、（11）式和（12）式中令ωn：=Φ(θn，vn)，得到（6）式.

引理3在X1，s()中，满足（6）式的任意序列是有界的.

证 明由（6）式，有：cm+ο(1)=Im(ωn)-因此可以得到的上界，又由引理1，可知{ωn(x，0)}在中有界，由（3）式和（6）式可知：

对于山路值cm，有以下估计：

引理4如果或者2s0，cm<此 外，如 果2s0，能得到相同的结论.

证明设φ0∈C∞(R+)满足：

且在引理1中，ωδ表示uδ的s-调和扩张，记：

由文献［22-23］可知：

且对任意p∈[2，2*s)，

由条件（f3）：

由（13）式和（14）式知，对于充分小的δ>0，gδ(t)有唯一的临界点tδ>0，这个临界点对应于其最大值点.因此，由g′δ(t)=0得到：

由（13）式和（14）式知：

因此可以得到：

由（15）式和（16）式，有：

接下来，区分以下情况：

（i）如果N>4s，则q>2>N(N-2s)，由（14）式和（17）式，得到：

由(2N-(N-2s)q)/2<2s<(N-2s)，令δ>0充分小，得出了结论.

（ii）如果

N=4s，则q>2=N(N-2s)，由（14）式和（17）式，得到：

由于4s-sq<2s，令δ>0充分小，得出了结论.

（iii）如果2s

如果4s(N-2s)(2N-(N-2s)q)/2，令δ>0充分小，得出了结论.如果N/(N-2s)(2N-(q+2)(N-2s))/2>0，当δ>0充分小时，仍可得出结论.

（iv）如 果2s

由 于(N-2s)2s-(N/2)，令δ>0充分小，可以得出结论.

（v）如果2s

选取λ=δ-θ且θ>(q-2)(N-2s)2，令δ>0充分小，可以得出结论.

引理5存在序列以及R>0，β>0，使得在（6）式中已经给出.

证明假设引理结论不成立，根据文献［4］的引理2.2，可以得出：

当n→∞时，对2

设l≥0，使得：

由引理1可知：

让上式中的n→∞，得到l≥(ksS(s，N))N(2s)，又由，这与引理4相矛盾.

定理1的证明设是（6）式中给出的序列，记是引理5中给出的序列.由引理3和引理5可知，存在的子序列，仍记为它本身，以及存在使得：

并且͂满足方程（2）.因此：

由于：

存 在 充 分 大 的T0>0，使 得Im((T0))<0，并 且Im((t))在t=1处达到严格的全局最大值.由cm的定义知：Im()≥cm.由于是任意的，可知bm≥cm.因 此 从（21）式 得 出 结 论：Im(͂)=cm=bm并 且(͂)=0.如文献［24］命题4.1.1那样讨论，可以得出͂∈L∞(RN).由于͂是非负的，并且是非平凡的，f是连续的，应用文献［11］引理4.9的Harnack不等式，可以得出͂是正的，因此，u(x)：=͂(x，0)是方程（1）的正基态解.