信息熵和多因素灰色系统模型在碳排放的分析与预测
阳建中,陈慧蓉,刘志先,赵荣阳
(1 北部湾大学 电子与信息工程学院,钦州 535011;2 北部湾大学 资源与环境学院,钦州 535011)
如今,气候变化已俨然成为了世界性的问题,其中全球变暖正是目前面临的重要变化之一.根据《巴黎协定》要求21世纪末全球气温升高控制在不超过工业化前2℃的目标,同时也要求各缔约方每5年提交一次“国家资助减排贡献”[1].即使每个国家都按协定来控制国家的排放量,但是也很难达到协议中的目标,全球升温可能达到3℃左右,无法真正实现不超过2℃的目标[2].而碳排放是引起全球变暖的重要因素之一,影响碳排放的因素有很多,包括产业结构、人口数量、生产生活方式、能源结构、GDP等[3].中国也颁发了一系列促进控制温室气体排放的法律法规.为了实现中国在2030年国内二氧化碳排放量尽量达到峰值,单位GDP温室气体排放比2005年下降60%~65%[4].国家采取了一系列的措施,包括调整产业结构、优化能源结构、能源效率提高、碳市场建设、生态碳汇增加等一些列措施,使得中国能源减排取得了一定的成绩[1].
目前很多学者对于碳排放分析和预测研究也取得了很多的成果,主要是集中在影响碳排的因素分析及碳排放的预测两个方面.对于碳排放的因素分析主要采用TOPSIS[5]、STIRPAT模型[6-7]、LMDI方法及其扩展[8-9],例如LEI等[10]利用了支持向量机方法分析了影响CO2的排放量的因素并给出预测.碳排放的预测也使用了很多现代的智能模型进行分析预测.近年来随着机器学习的兴起,机器学习也被用到了碳排放预测中,例如长短记忆方法(LSTM)[11],神经网络[12]等方法.王珂珂等[12]先使用STIPRAT模型将影响碳排放的重要因素筛选出,然后再利用极限学习机(ELM)及BP神经网络(BPNN)对碳排放量进行预测.还有包括面板回归模型、逻辑回归模型[13]、STIRPAT模型[7,14]、非线性灰色伯努利模型(NGBM)[15].SUN[16]将粒子群优化极限学习机应用到了河北省的碳排放的预测中.FANG等[17]改进了粒子群算法并优化高斯过程回归方法(PSOGPR),对不同国家的CO2排放量进行了预测.
上述方法都取得了较好的效果.但是因素分析部分只是对很影响碳排放的因素进行了分类,没有给出具体的影响程度,无法直观的给出数据化的结果.预测部分的很多方法比较复杂,不容易实现.碳排放量官方统计往往只有近20年来的数据,样本量小,导致某些要求样本量大的智能方法预测的精度偏低.本文利用信息熵和灰色系统理论方法分别分析了影响碳排放因素程度的大小并预测.
1 数据来源与处理
1.1 数据来源
根据研究需要及数据可得性,选取广西能源消费、地区生产总值、人口、工业生产总值等数据,其中能源消费数据来源于1997-2018年的《中国能源统计年鉴》,地区生产总值、人口、产业结构等数据来自1996-2018年的《广西统计年鉴》;R&D人员、研究与试验发展经费支出、公共财政支出等数据来源于《广西科技统计数据》.为了保证数据的准确性,选取数据尽可能完整的年份,本文选择2006年到2016年的数据.需要说明的是,部分缺失的能源消费数据经分段三次埃尔米特插值法后获得.
1.2 数据标准化
广西能源消费碳排放量,采用国际公认的IPCC碳排放计算模型获得,在研究时间段内广西的化石能源消费主要为原煤、原油、汽油、柴油,因此,碳排放计算时仅包括几种因素.关于碳排放影响因子选取,宋旭等人[18]的研究中采用能源碳排放系数、能源结构、能源强度、经济发展水平、人口、科技发展水平等作为影响因素.其中,能源碳排放系数为各种能源碳排放量与该能源消耗量的比值之和,一般情况下能源碳排放系数保持不变;能源结构为各种能源消费量分别与总能源消费量的比值之和;能源强度为能源消费总量与地区生产总值之比;经济发展水平的主要衡量指标为人均地区生产总值;技术进步主要指R&D人员与总人口的比重,研究与试验发展经费支出占公共财政支出的比重.但根据数据相关系分析结果显示,R&D人员与总人口的比重,研究与试验发展经费支出占公共财政支出的比重与广西碳排放量仅存在较小关联性.因此,丢弃该指标.标准化后的数据如表1所示.
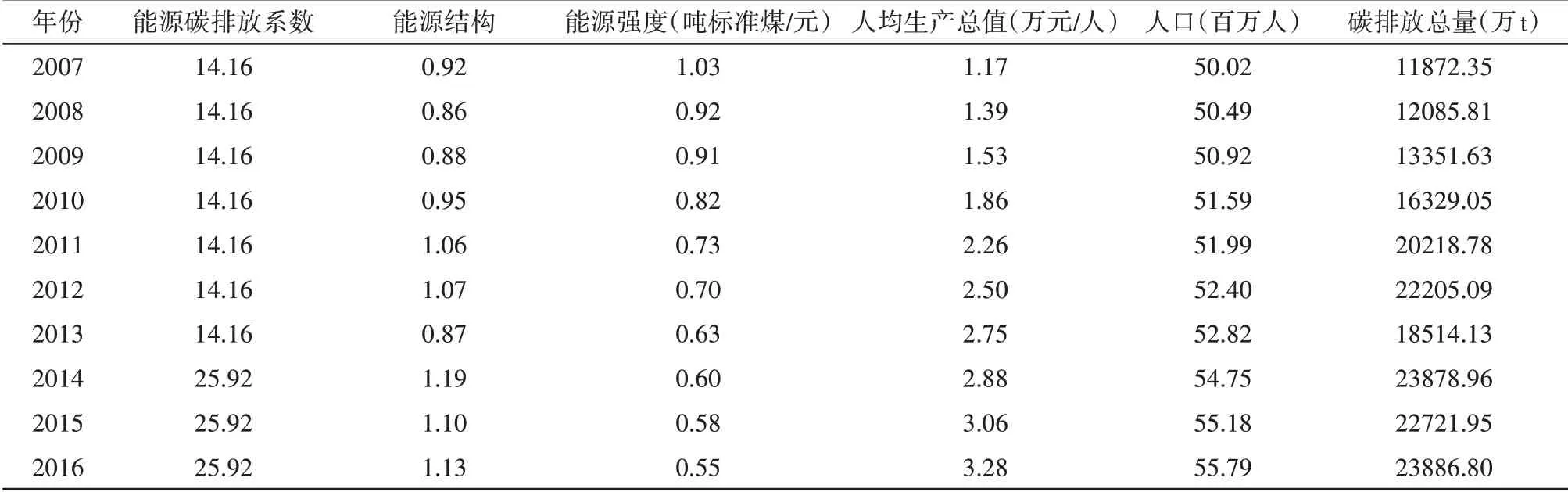
表1 广西能源消费碳排放量及影响因子值Tab.1 Carbon emission and influencing factor values of energy consumption in Guangxi
2 信息熵及灰色关联预测模型构建
2.1 信息熵
信息熵是由数学家香农提出来的,它是衡量集合离散度的指标之一,也可以反映不同数据序列的所含的信息量[19],其应用也非常广泛,例如图像分类[20]、水资源管理[21]等.为了分析人口、能源结构、能源强度、GDP与碳排放的关系,将前四个因素设为xi(i=1,2,3,4),每个因素中包含了n个数据.因此,每个因素构成了一个序列,利用信息熵方法计算出每个因素包含的信息量,即权重.pij(j=1,2,…,n)为每个因素里数据对应的概率:
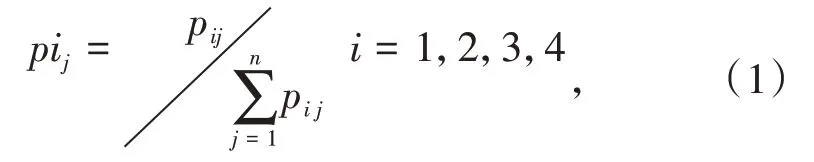
假设将影响碳排放的因素序列xi,构建对应的函数I(xi),利用信息论中计算方法,可以利用下面公式得到信息熵:
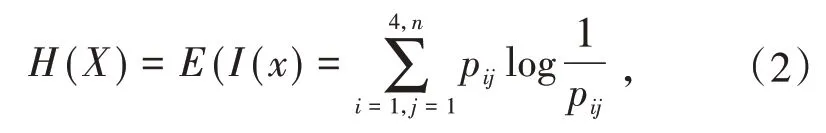
H(X)表示的是样本数据X的信息熵值.
2.2 G(1,N)模型构建
灰色系统的状态模型揭示出灰色系统内部变量相互作用并连续发展的过程,所以可以用内部变量的相互作用的表征数据,即用离散的时间序列数据根据收敛原理建立近似连续的微分方程模型,记为GM(m,n),其中,m为阶数,n为变量的数量[22].
根据需要处理的因素或者特征数为单个或者多个设置模型.当m=1,n=1时,GM(m,n)为G(1,1),为一阶单变量因素预测模型.若n>1时,则为多变量/因素预测模型.本文利用人口、能源结构、能源强度、GDP四个因素预测碳排放量.因此,本文采用了多因素模型,且用碳排放的序列作为特征数据序列,记为:

设人口、能源、GDP、第二产业产值因素为相关因素序列:
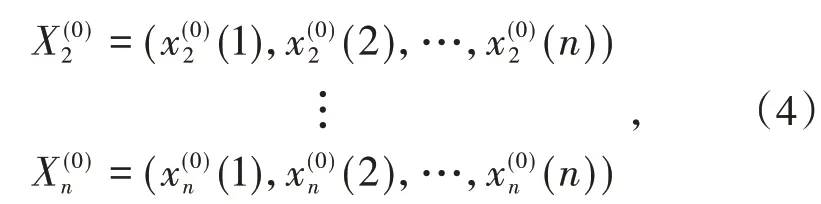
令(i=1,2,…,N)的(1-AGO)序列为Xi(1),Z其中
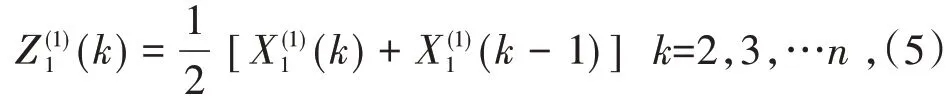
则,GM(1,n)模型为:
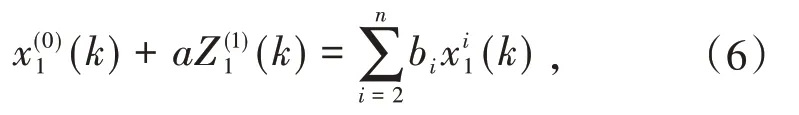
其中,系数a称为发展系数,bi为驱动系数,bix(1)i(k)为驱动项.

再 设b=(a,b1,b2,…,bn)T,由 最 小 二 乘 参 数 估 计可得
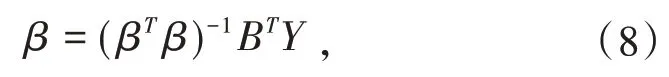
当(i=1,2,…,n)变化幅度较小时,GM(1,n)可以近似为:
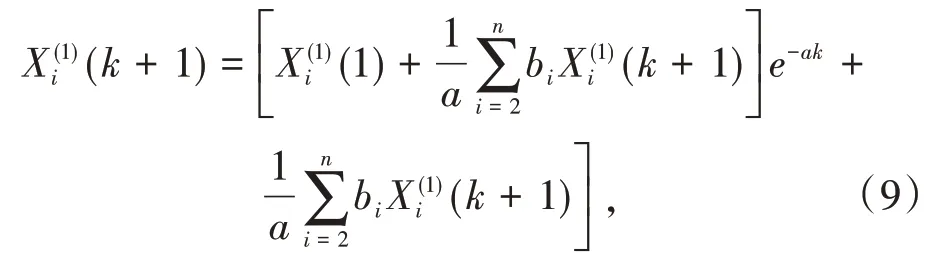
累减还原式为:
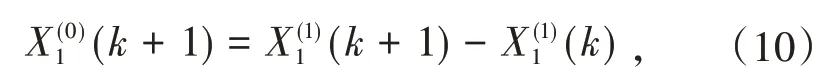
差分模拟式为:
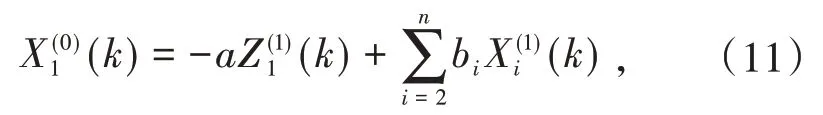
当k=1,2,3,…,n-1时,计算得到的是灰色系统拟合的值;当k≥n时,可计算得到灰色系统预测的值.
2.3 模型的检验
为了对模型拟合的效果进行检验与评价,需要把预测数据和真实数据进行对比分析,检验的方法主要是有残差检验、关联度检验和后验差检验等方法.其中后验差检验是比较常用的方法.其检测过程如下:
残差序列为:

原始数据的均值:
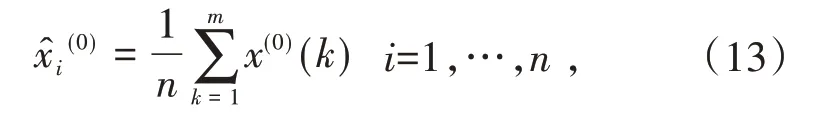
残差序列的平均值:

原始序列的方差:
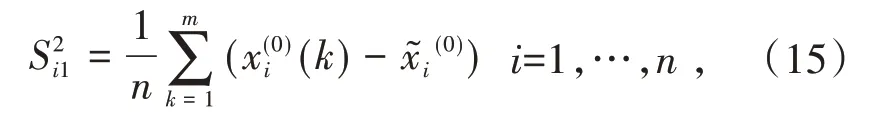
残差方差:
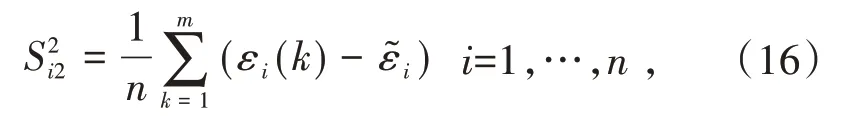
后验差的检验为:
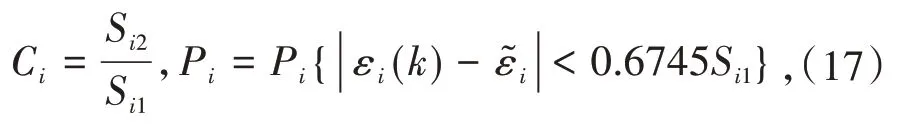
使用后验差来检验模型,通常考虑后验差值的比值C和小误差概率P,这两个指标可有式(17)计算得出,预测精度等级划分如表2所示.
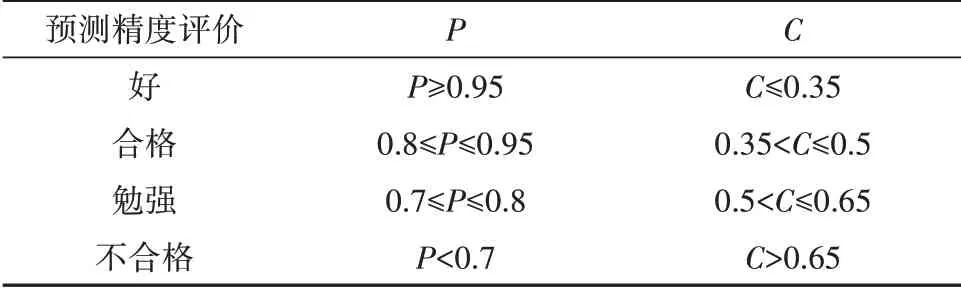
表2 后验差预测精度等级划分表Tab.2 A posteriori error prediction accuracy classification table
3 结果与分析
3.1 碳排放分析
为了更好地分析不同因子与碳排放的关系,从时间序列和因子两个维度分别计算相应的信息熵.第一种是使用年份作为时间序列,计算每年的信息熵.利用每个年份不同的因素作代入到公式(2)中,然后可以计算出不同年份信息熵的值.第二种是计算某一个要素所有从2007年到2016年,该要素对应的值代入公式(2)中计算得出该要素的信息熵.
通过图1(a)可以看出碳排放量整体上是呈现上升趋势.但是在2012年到2014年之间存在了较大的波动,其中2012年碳排放大幅减少,2013年出现了大幅的回升状态.信息熵越大,说明信息量越大,反之,信息量越小;信息熵曲线斜率越大,说明系统信息突变的可能性越大,反之,系统信息的有序性越大.图1(b)呈现了对应的年份信息熵的值,从2007年到2016年的十年期间广西碳排放信息熵整体上呈现稳定下降的趋势,其中2013年的信息熵值出现了小幅度的增加,表明广西能源消费碳排放系统朝有序方向发展,可预测性增强.其中由于12年、13年碳排放量出现了波动,表明了广西碳排放正在得到有效的控制.为了进一步分析广西能源消费碳排放系统中不同因子对碳排放的影响程度,本文进一步分析各因子与碳排放关联程度(如图2所示).
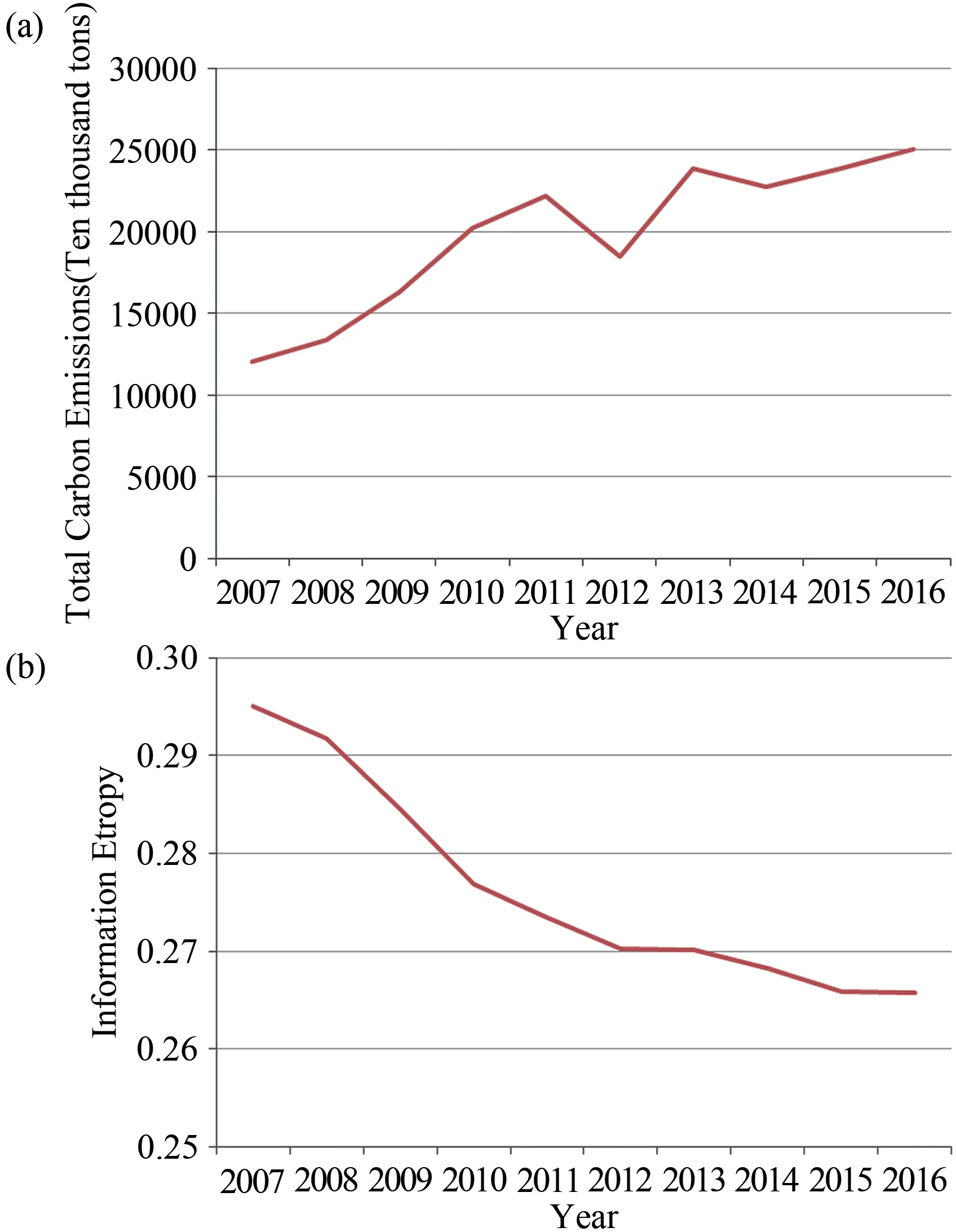
图1 2007年到2016年的碳排放量和对应的信息熵Fig.1 The carbon emission from 2007 to 2016 and the corresponding the information entropy
利用灰色系统分别计算了能源结构、能源强度、GDP、人口与碳排放的相关程度.从计算的结果(图2)可以看出GDP对碳排放的影响最大,达到75.98%;其次是人口因素,其对碳排放的贡献程度超过70%;能源结构对碳排放的贡献程度最小,但是也超过了50%.

图2 各因素与碳排放的关联度Fig.2 The correlation of different factors with carbon emission
从图3中分析可知,广西能源消费碳排放系统各要素的信息熵从高到低依次是人口、能源结构、能源强度、碳排放、人均GDP,都介于0.322到0.332之间,相差比较小,表明了五个因素在10年间对碳排放的影响都比较稳定,只有人口和能源结构相对于其他要素存在一些小幅度的波动.表明二者对广西能源消费碳排放系统的影响相较于其他因子具有较高的不确定性.
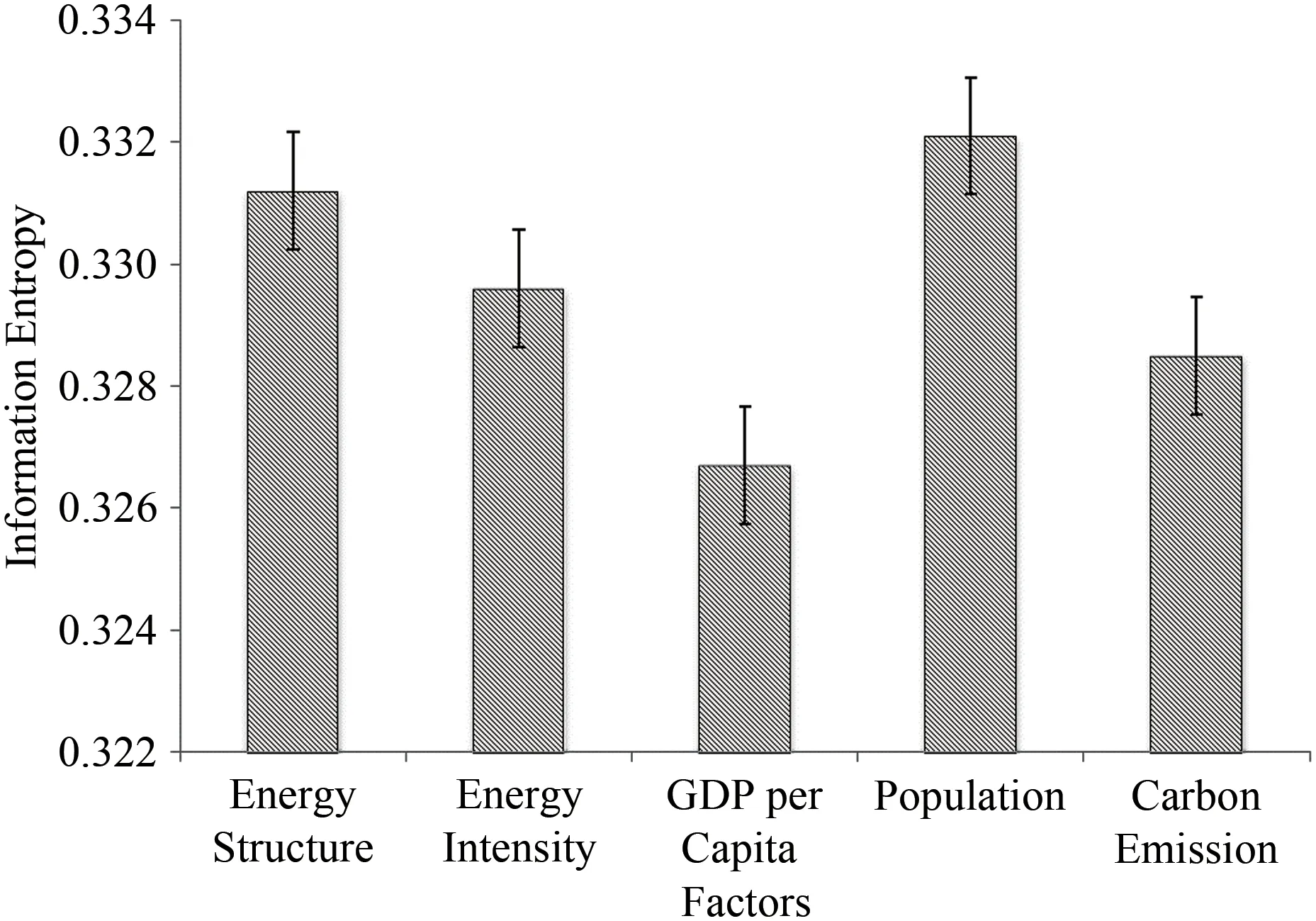
图3 不同因素的信息熵Fig.3 The information entropy of difference factors
3.2 模型预测及分析
通过从2007年到2016年的广西碳排放的真实值可知,碳排放量整体上呈现增长的趋势,其中2013年到2014年出现了一些波动值.因此,在2012年后的真实值出现了一些波动.利用Matlab 2017a实现了模型得出预测结果,并绘制出了实际值与预测值的对比折线图,如图4所示.
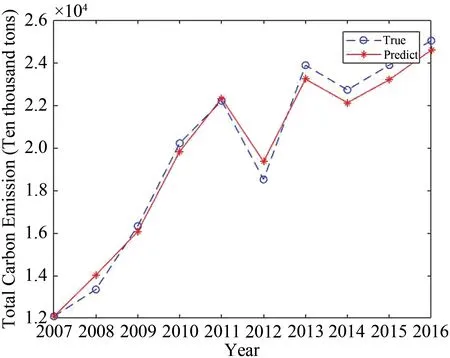
图4 预测值与真实值比较Fig.4 The comparison of the true value and the prediction
利用灰色系统计算出的碳排放的真实值与预测值的偏差都小于1000,相对误差都控制在5%以内.预测精度P=0.98,C=0.14,可见模型预测精度较好.
4 结论
信息熵方法可以实现任意变量之间的空间相关的定量分析.由于数据量小,分析不同要素的在时间上的稳定性.应用灰色系统理论建立了多因素的预测模型,通过分析残差检验,得到灰色系统预测模型.实验结果表明,预测模型的精度好.利用灰色系统进行预测分析具有数学模型简单、易建立、数据样本少等优点.

