具有粗糙核的双线性Hardy算子交换子在λ－中心Morrey空间中的有界性

徐琪,喻晓,马江山*

(1.东华理工大学 理学院,江西 南昌 330013;2.上饶师范学院 数学与计算机科学学院,江西 上饶 334001)

1 引言及主要结论

设f是R＋上的非负局部可积函数,则Hardy算子H定义为:

显而易见,Hf(x)≤Mf(x),其中Mf(x)是Hardy－Littlewood极大函数,其定义如下:

这里的I为包含x的任意方体。

对Hardy算子H而言,我们有如下著名的积分不等式[1]:

其中1＜p＜∞,且常数是(1)式右端的最佳常数。

令f是Rn上非负局部可积函数,则高维Hardy算子定义为:

对任意的λ≠0,若函数Ωx()满足Ωλ(x)＝Ωx(),则称Ωx()为零次齐次函数。假设Sn－1为Rn上的单位球面,当时,具有粗糙核的高维Hardy算子定义如下:

Hardy型算子在函数空间中的有界性引起了数学工作者的极大兴趣,介绍此类算子在函数空间中的有界性之前,我们引入下列几类重要的函数空间。

并且他们证明了此算子在λ－中心Morrey空间中的有界性。

双线性Hardy算子及具有粗糙核的Hardy算子交换子都引起了数学工作者的极大重视,受上述文献启发,本文将讨论如下具有粗糙核的双线性Hardy算子交换子,其定义为:

其中:

本文主要结论如下:

注记1.2 本文主要结论推广了文献[7－9]中的相关对应结果。

2 主要结果的证明

接下来分别估计Ⅰ和Ⅱ。

对于Ⅰ,令Ck＝{x|2k－1≤|x|＜2k}(k∈Z),可对Ⅰ做如下分解:

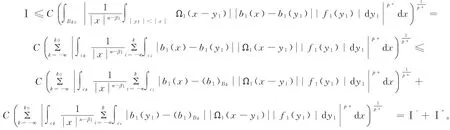
对于Ⅰ′,我们有:

因为,

所以有:

接下来对Ⅱ进行估计,有:

类似于(9),有:

至此,利用Ⅰ和Ⅱ的估计结果以及定理1.1的条件,我们有:

再依据λ－中心Morrey空间的定义,可得(3)式。最终定理1.1得证。