周期环境中年龄等级结构种群模型分析

窦艺萌, 何泽荣

(杭州电子科技大学运筹与控制研究所, 浙江 杭州 310018)

1.引言

在许多不同种类的生物种群所构成的“小社会”中, 生态学家都观察到了个体之间存在等级或社会地位差异, 参见文[1]及其所引用的200余份文献.为了对种群的演化趋势作出比较可靠的预测, 数学模型法是一种得到普遍认可的途径.目前, 已有一些研究者为具有等级结构的生物种群建立数学模型并作出理论分析.[2-8]这些工作主要关注模型的基本性质(如适定性、数值方法), 以及种群的持续生存和灭绝条件.尽管现有工作还很不完善, 但其重要性不容置疑,它们是后续研究的出发点.

与其它结构化的种群模型(如年龄结构、尺度结构)不同, 等级结构模型均为非线性的, 而非线性系统的彻底分析都比较困难.由于受季节变化等周期性因素的影响, 种群的个体生命参数常常经历周期性振荡.这种现象在等级结构类建模时尚未被考虑过.有鉴于此, 本文提出一类周期环境中的等级结构种群模型, 在一组较为合理的参数条件下, 确立模型解的存在唯一性和非负性, 为后续研究种群系统的长时间演化行为和调控问题奠定基:.

2.模型与参数条件

假设个体的出生率和死亡率随时间周期性变化, 考虑下列种群模型:

其中, R+=[0,+∞),Q=(0,A)×R+;A是种群个体的最大年龄,T为生命参数变化周期.其他状态变量和参数的含义如下:p(a,t)表示t时刻年龄为a的个体密度;f(a,t)是外界向种群生存环境的迁入率;E(p)(a,t)表示在t时刻年龄为a的个体所面临的内部环境;β(a,t,E(p)(a,t))和μ(a,t,E(p)(a,t))分别表示t时刻年龄为a的个体的出生率和死亡率,也与内部环境相关.

本文的基本假设如下:

对∀s1,s2∈[0,M],∀(a,t)∈Q均成立;

(A4) 对∀(a,t)∈Q, 函数β(a,t,·)在Q上是非增的,μ(a,t,·)在Q上是非减的;

(A5) 对∀(a,t)∈Q, f(a,t)≥0, f(a,t)=f(a,t+T),f ∈L∞(Q).

3.解的适定性

将模型(2.1)中函数μ, β里的p固定为非负函数q, 由此得到以下线性模型:

由基本假设易知K满足

0≤K(t,s;q)≤K(t,s;0)≤β(s,t,0),a.e.(t,s)∈R+×(0,A).

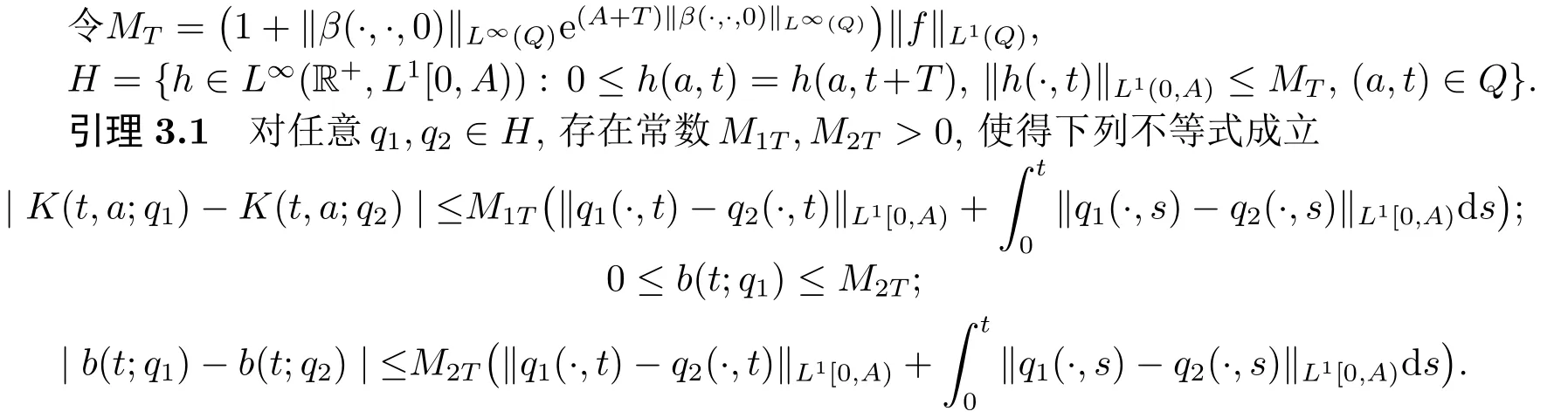
证由内部环境的定义知

由(3.4), (3.6)及(3.8)式可得

其中M1T=L(MT)max{1,‖β(·,·,0)‖L∞(Q)}.

又由(3.4), (3.7)-(3.8)可得

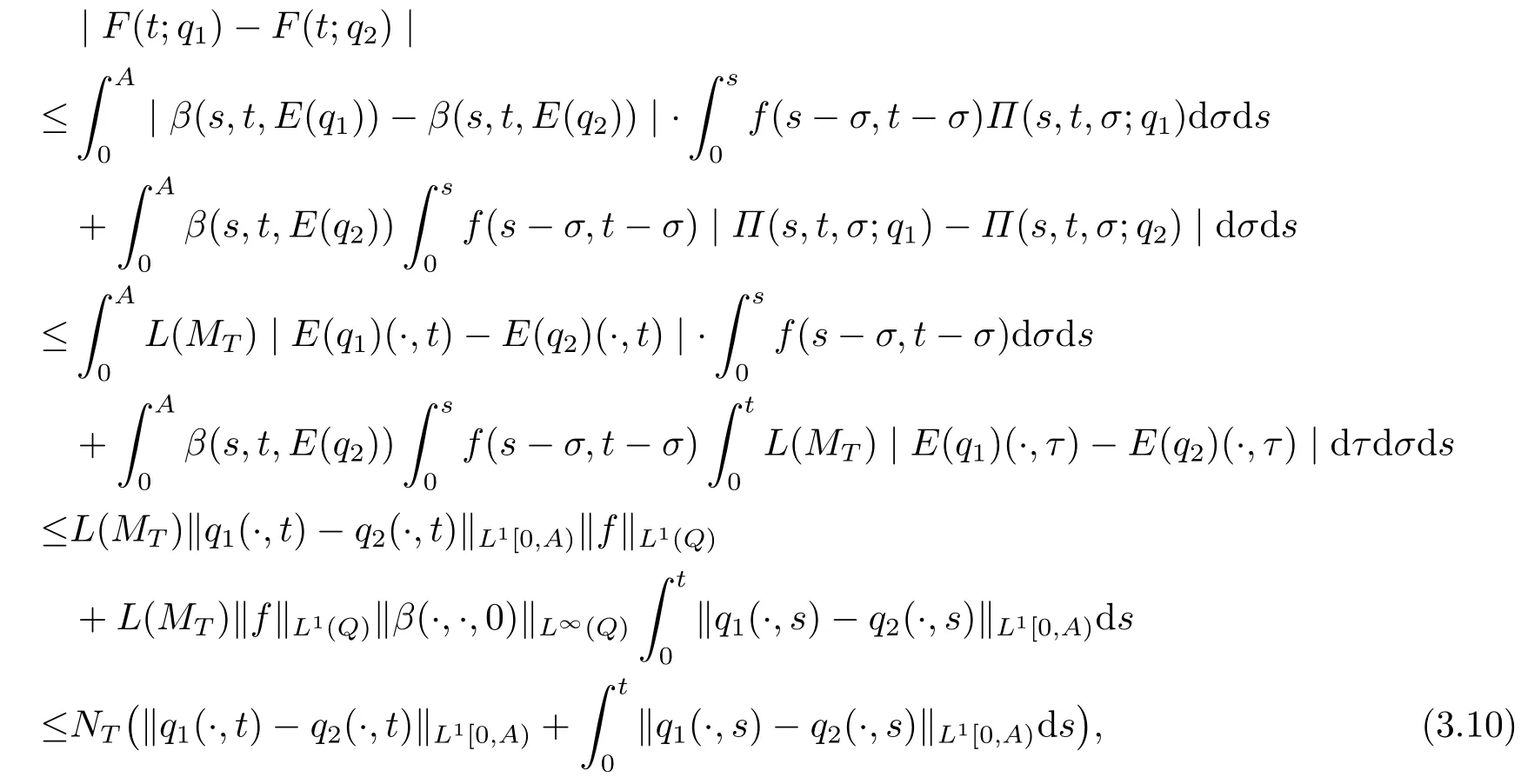
其中NT=L(MT)‖f‖L1(Q)max{1,‖β(·,·,0)‖L∞(Q)}.

由于函数b具有周期性, 可限定t ∈[A,A+T].由(3.5)及Bellman不等式可得出

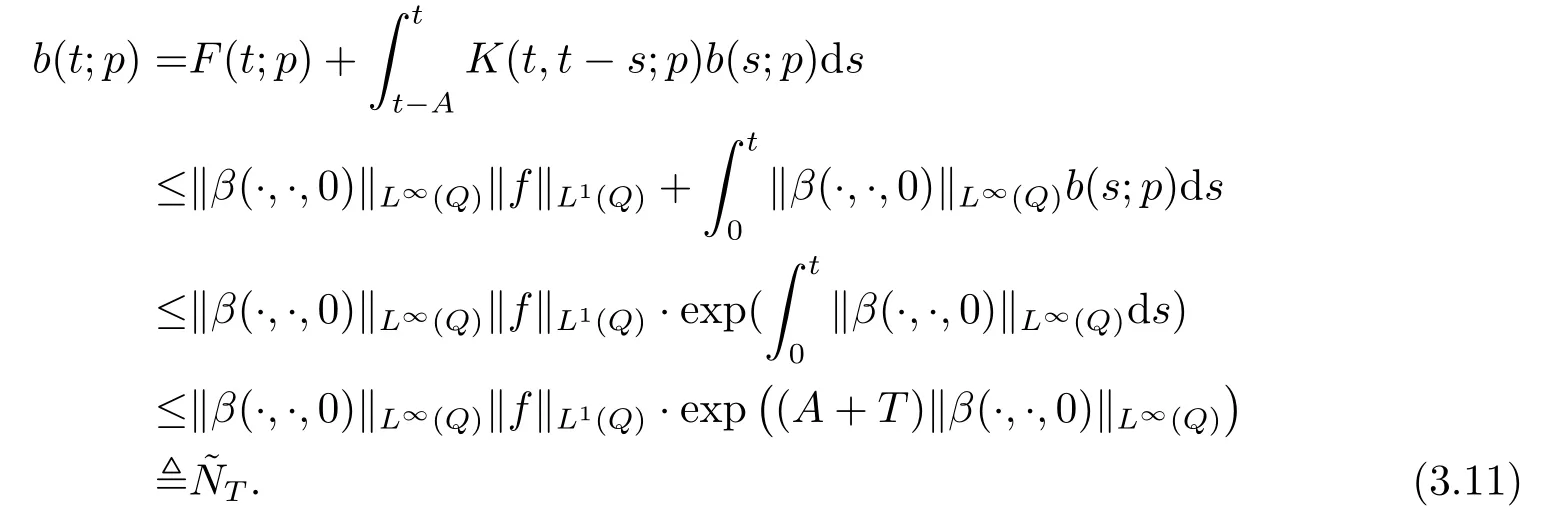
再利用(3.5)及(3.8)-(3.11)可知

利用(3.12)及Gronwall不等式导出

定义映射:

T:H →L∞(R+,L1[0,A)),

(T q)(a,t)=p(a,t;q), ∀q ∈H; (a,t)∈Q,

其中p(a,t;q)是由(3.3)给出的线性系统(3.1)的解.

定理3.1系统(2.1)存在唯一的解, 且该解是非负有界的.

证由于H中的函数关于t的周期性, 可将t限定在固定区间[A,A+T]内.取定正数λ使得λ ＞在H中定义等价范数:

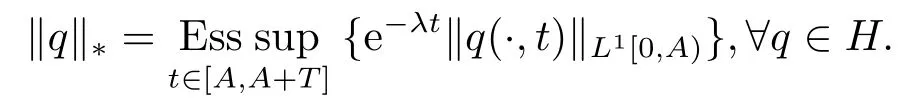
因此, 对∀q1,q2∈H, 由引理3.2可导出

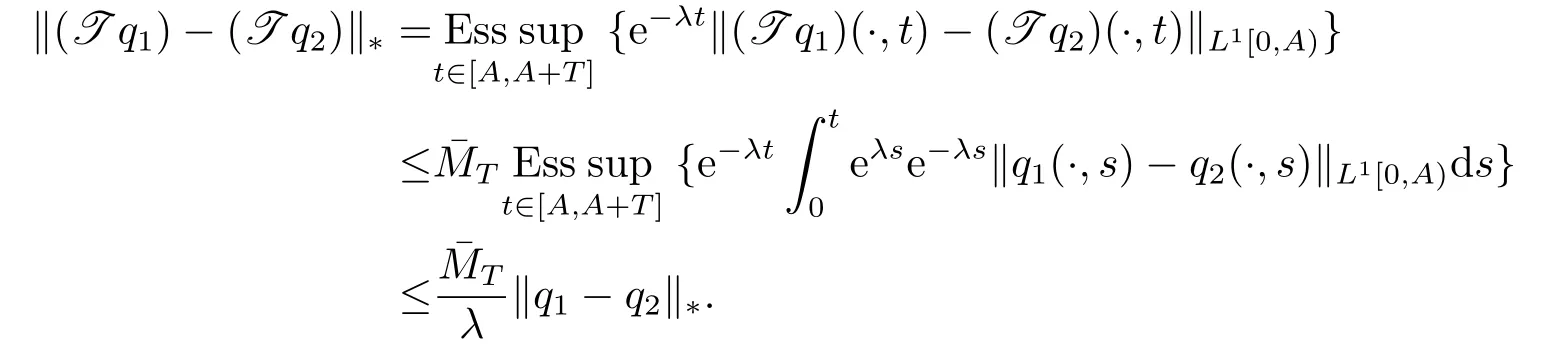
上述不等式表明T为空间H中的压缩映射, 它在H中存在唯一的不动点, 该不动点即为系统(2.1)的解.再据(3.3)知该解非负有界.定理证毕.

注3.1当a,t,s)≡0, α →1时, 上述定理3.1就退化为专著[9]中的定理2.4.2.此外, 容易验证: 定理3.1也推广了文[10-11]的相应结果.