不确定离散时间输入饱和系统的鲁棒预见控制

李丽 于晓

(1.湖北经济学院信息管理与统计学院, 湖北 武汉 430205; 2.山东建筑大学理学院,山东 济南 250101; 3.湖北经济学院湖北数据与分析中心, 湖北 武汉 430205)

1.引言

预见控制是一种利用已知的未来目标值或未来干扰信息来改善闭环系统动态响应, 抑制外界扰动, 提高系统跟踪精度的控制方法[1].预见控制的思想起源于20世纪60年代, 经过50多年的发展, 学术界已经建立了离散时间线性系统、连续时间线性系统的完整理论, 并且在广义系统预见控制理论、随机系统预见控制理论等方面有了一些进展[2-4].近年来, 相关学者将预见控制与一些有效的控制方法结合, 建立相应的预见控制理论.文[5]提出了信息融合的最优预见器设计问题, 利用对象动态方程约束信息、输出测量信息、未来信息等, 基于融合估计理论得到最优控制序列.文[6]研究了连续时间系统的H2前馈干扰抑制问题.针对含有输入输出时延的连续系统的H2预见控制问题, 采用了对外部输入延时的等效方法将其转化为LQ问题, 再利用最优性原理来求解.文[7]考虑一类时滞系统的干扰预见控制问题, 将原系统的预见控制问题转化为H∞控制问题, 并分析求解相应的Riccati方程而确定预见控制增益矩阵.由于基于Riccati方法的预见控制设计方法不具有一般性, 文[8-10]结合线性矩阵不等式技巧和误差系统方法提出了控制系统的鲁棒预见控制问题, 给出被考虑对象的预见控制器设计方法.然而, 就目前的研究状况来看, 预见控制理论和其它控制相结合成为了发展的趋势.例如文[11]将预见控制与非线性控制相结合, 能直接基于非线性模型进行设计, 提高非线性系统的控制性能.为了解决参数变化较大的不确定系统的预见控制问题, 文[12]结合预见控制和自适应控制, 提出了多模型自适应预见控制的问题, 减少对系统模型的依赖, 提高鲁棒性和自适应能力.文[13]研究了线性离散时间系统的容错预见控制, 基于系统的状态和故障估计, 给出了预见控制器的设计方法.在一些实际问题中, 如果在设计控制器的时候忽略了输入信号大小和变化率的饱和限制, 会使得设计的系统性能恶化甚至出现不稳定.而上述这些成果并未考虑输入饱和下的预见控制问题.

这里, 本文针对一类带有输入饱和的不确定离散时间系统, 利用预见控制理论研究中构造误差系统、通过提升把可预见的目标值信号和干扰信号加入扩大误差系统的方法应用到输入饱和不确定系统的预见控制中, 研究不确定系统的鲁棒预见控制问题.

全文沿用如下记号:Rn,Rn×n分别表示实数域上的n维向量空间与n×n矩阵空间;P ＞0表示P为对称正定矩阵,P ＞Q表示P -Q ＞0; diag{M1,M2,··· ,Mn}表示对角元素为Mi,(i=1,2,··· ,n)的对角矩阵.sym(A)表示A+AT;A(i)表示矩阵A的第i行;l2[0,∞) 表示为平方可和的向量集合.I表示适当维数的单位矩阵.

2.问题描述及假设

考虑不确定离散时间饱和系统:

其中,x(k)∈Rn为状态向量,u(k)∈Rq为输入向量,y(k)∈Rq为输出向量,w(k)∈Rl为干扰向量且满足w(k)∈l2[0,∞).A,B,C和E为适当维数的常数矩阵.ΔA(k), ΔB(k),ΔE(k)和ΔC(k)是关于时间变量k的不确定矩阵.

由于系统的输入不可避免受到饱和约束的限制,um(k)∈Rq的描述如下,

其中, 饱和函数sat(·)的定义为

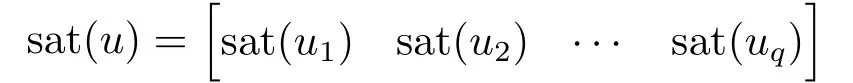
这里, sat(ui)=sign(ui)min{|ui|},i ∈{1,2,··· ,q}.不失一般性, 我们假设饱和的上界是1,即sat(ui)=sign(ui)min{1,|ui|}.

关于系统(1), 我们给出以下基本假设

注1(A1)是预见控制理论中常用到的假设条件.

(A2)是鲁棒控制中常用的假设, 式(3)指的是系统(1)中的不确定项满足一定的匹配条件;而式(4)指的则是不确定项是范数有界的.

(A3) 设目标值信号r(k)∈Rq的预见步数为MR,即在当前时刻k,r(k),r(k+1),r(k+2),···,r(k+MR)为已知.

r(k+j)=0,j≥MR+1.

(A4) 设干扰信号w(k)∈Rl的预见步数为Md,即在当前时刻k,w(k),w(k+1),w(k+2),···,w(k+Md)为已知.

w(k+j)=0,j≥Md+1.

注2(A3)和(A4)是预见控制理论的标准假设[1-5], 表明只有一段时间的可预见信号对系统的性能有较明显的影响, 预见步数以外的信号的值对系统的影响不大.

3.扩大误差系统的推导

首先通过引入一个与状态变量有关的辅助变量, 并用系统状态向量与相应辅助变量之差代替通常的状态差分, 避免对时变矩阵和饱和输入项取差分, 构造出扩大误差系统.

受文[3]的启发, 我们构造

其中xs(k)是适当的辅助变量, 从(A1)知可以取

其中

定义跟踪误差信号

根据式(1)、(5)和(6)得到

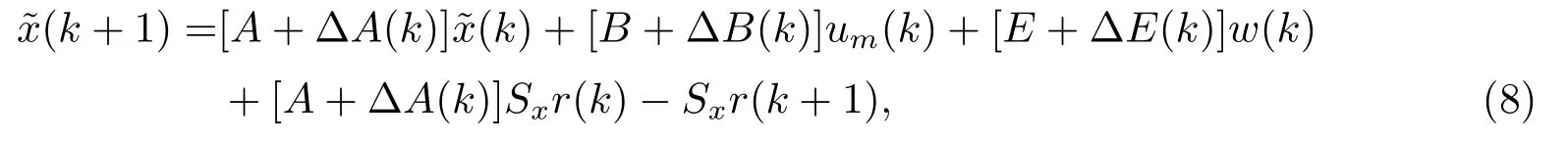
同时

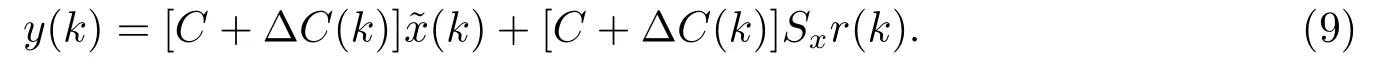
另外

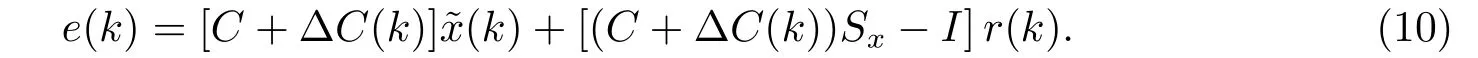
令

依据(A3)和(A4)可得到

通过式(8), (11)及(12)可得

其中

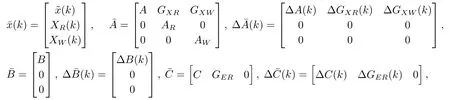
而且

注意体现预见信息的XR(k)和XW(k)是状态向量的一部分, 系统(13)包含了可预见的目标值和干扰信号的信息.

进一步, 我们得到

注意不确定矩阵仍满足

为消除静态误差, 我们引进离散积分器, 它由下式定义

结合式(13)和式(18)得到

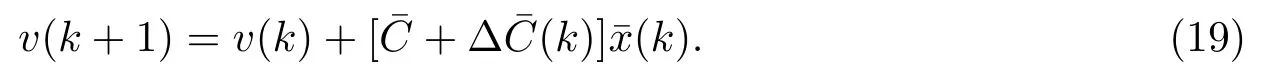
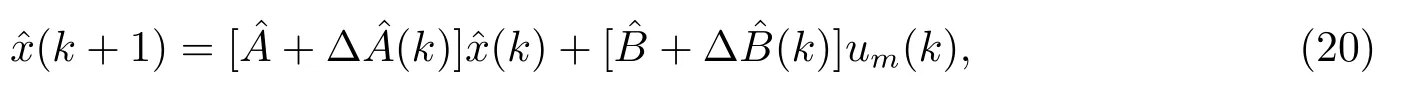
这里

由式(14), (15), (16)可以验证系统(20)中不确定矩阵可表示为

由式(17)可知, 不确定矩阵依然满足

结合式(13)和(20),e(k)可表示为

根据式(24), 易得如果能够设计出式(20)的一个反馈控制器, 使得式(20)的闭环系统渐近稳定, 那么相应的系统(1)的闭环系统就实现了y(k)对r(k)的跟踪.

4.预见控制器的设计

P是一个适当维数的正定矩阵.令

定义ψ(u) =u-sat(u), 得到的ψ(u) = [ψ(u1)T··· ψ(uq)T]T是一个死区非线性函数.显然, 我们有ψ(ui)=ui-sat(ui),i ∈{1,2,··· ,q}.

引入如下引理:

引理1[14]对于正定的对角矩阵J和适当维数矩阵H和W, 若ˆx(k)∈LH,

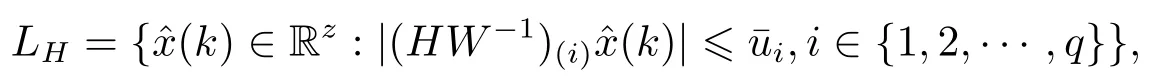
则ψ(u)TJ[u-ψ(u)+HW-1(k)]≥0.

引理2[15]对于给定适当维数矩阵Y=YT,E,H和F, 且F满足FTF≤I,若存在参数ε ＞0,使得Y+εHHT+ε-1ETE ＜0,则

引理3[16]如果L,H并且H ＞0, 则

引理4[17]对于适当维数的矩阵T,W,S和矩阵N及标量β, 如果不等式

满足, 则不等式T+STWT+WS ＜0成立.

如果能够设计出系统(20)的一个状态反馈

这里,K是待定的参数矩阵.

根据式(20)和式(26)得到闭环系统为

定理1对于正定的对角矩阵J, 如果存在矩阵X ＞0和矩阵W,Y和H使得

成立, 则闭环系统(27)在ε(P)内是鲁棒渐近稳定的.且ε(P)是闭环系统的一个稳定区域.

证考虑如下Lyapunov函数

这里P ＞0.

根据引理3, 可知式(29)可保证

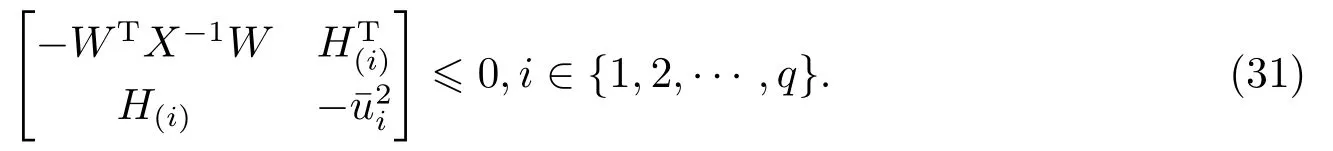
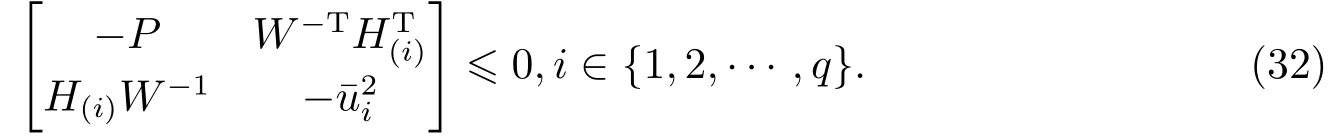
另外, 对式(32)使用Schur补引理, 可以进一步得到

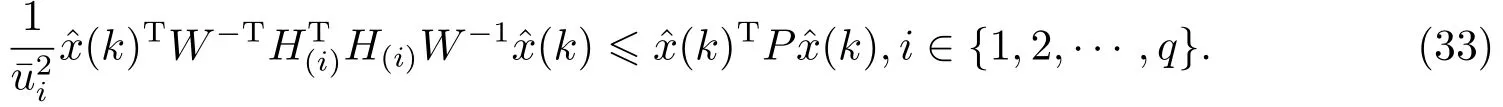
对于∀ˆx(k)∈ε(P), 由式(33)易得ˆx(k)∈LH, 因为V(ˆx(k))≤1.

同理, 根据引理3, 式(28)可以保证

另外, 在式(34)的左边和右边分别乘以diag{W-T,I,I}和diag{W-1,I,I}, 同时令P=X-1,K=Y W-1, 我们有

运用Schur补引理, 式(35)等价于

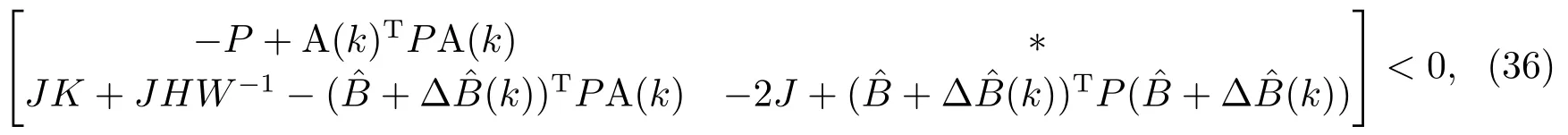
这里

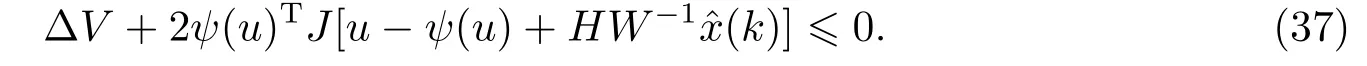
根据引理1并结合式(33)和(37), 对于所有的ˆx(k)∈ε(P){0}, 我们可以得到ΔV(ˆx(k))＜0, 这就表示系统(27)在集合ε(P)内是渐近稳定的.

另一方面, 注意到ΔV ＜0,∀(k)∈ε(P){0}.我们有

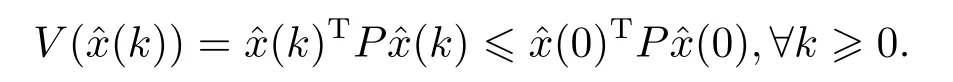
下面利用LMI方法给出闭环系统鲁棒渐近稳定的条件.

定理2对于对角正定矩阵J, 如果存在矩阵X ＞0和矩阵W,Y和H及参数εi ＞0,i=1,2,使得

成立, 则闭环系统(27)在ε(P)内是鲁棒渐近稳定的, 其中状态反馈增益矩阵为K=Y W-1, 控制输入为u(k)=Y W-1(k).

证为了叙述简捷, 用Ψ表示式(28)左边的矩阵.把Ψ的不确定部分分离出来,并结合式(21)和(22)得到

其中,

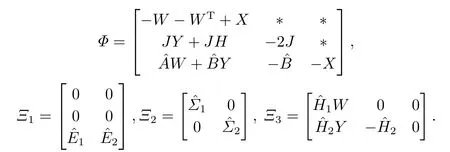
由式(23)可知≤I, 对式(40)右边后两项应用引理2, 令Λ=εi ＞0,i= 1,2,得到

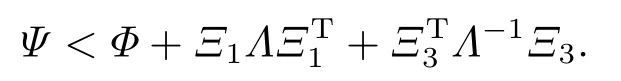
因此, 如果存在ε1＞0,ε2＞0使得

就有Ψ ＜0, 从而定理1的条件满足.因此只须给出式(41)成立的条件.根据引理2易得知式(38)成立可以保证式(41)成立, 因此根据定理1知, 定理2成立.

对增益矩阵K进行分解

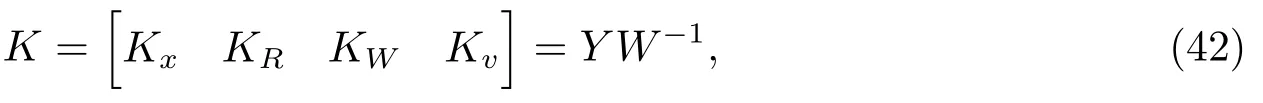
这里

则式(26)可写为

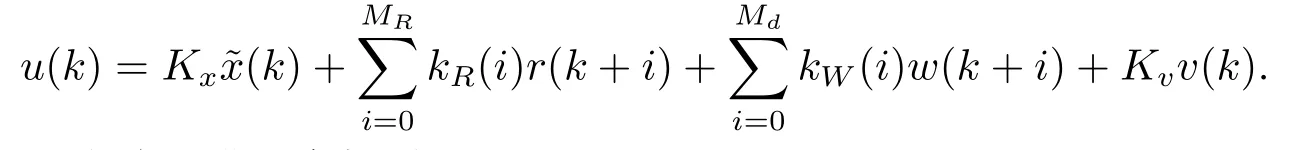
根据式(5)和(6), 上式可进一步得到

由上式看出, 系统(1)的带有预见作用的控制器由5部分构成: 第1部分为状态变量反馈项;第2部分为基于未来目标值信号的预见前馈补偿项; 第3部分为基于未来干扰信号的预见前馈补偿项; 第4部分是跟踪误差的积分; 第5部分是关于状态辅助变量信号的补偿.

针对系统(20), 输出方程取为

其中

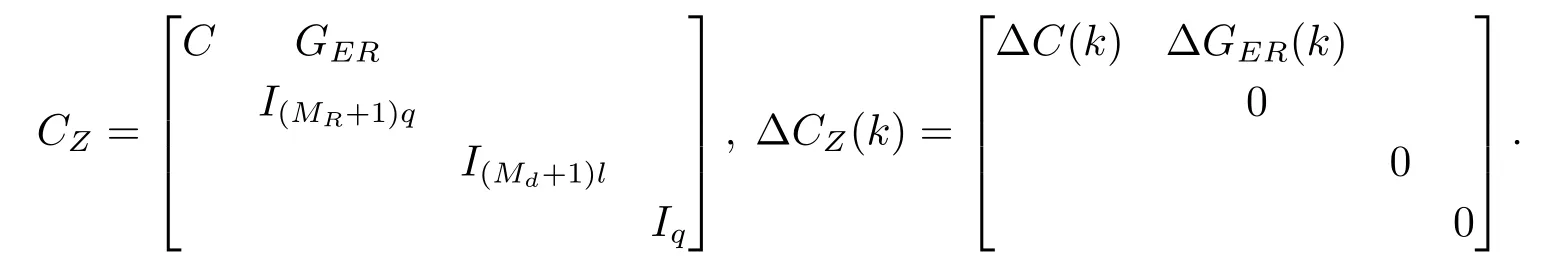
改写后的输出方程使得我们设计的输出反馈控制器带有预见反馈项和误差积分项, 达到改善闭环系统的跟踪性能和消除静态误差的目的.

根据式(3)和(4)有

针对系统(20), 考虑如下形式的一个输出反馈

根据式(20)和(46)得到闭环系统为

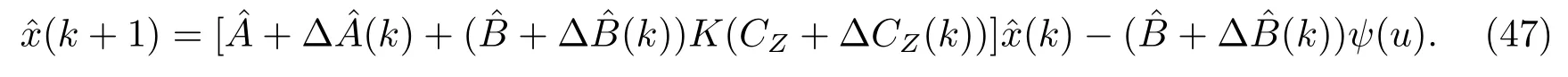
定理3对于正定的对角矩阵J, 参数β及矩阵Q, 如果存在矩阵X ＞0和矩阵W,L,H和可逆矩阵U使得

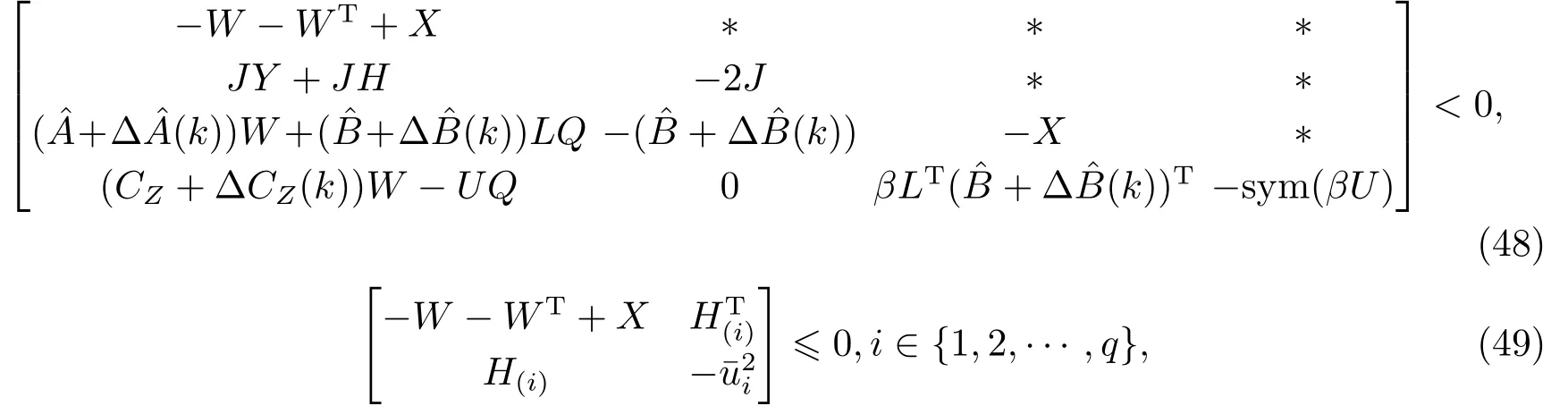
成立, 则闭环系统(47)在ε(P)内是渐近稳定的.

证根据引理4可知, 式(48)可以保证

令K=LU-1, 则式(50)就是

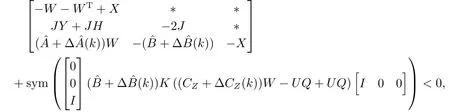
即

根据定理1可知, 定理3成立.

下面我们把它转化为不含不确定参数的LMI.

定理4对于正定的对角矩阵J, 参数β及矩阵Q, 如果存在矩阵X ＞0和矩阵W,L,H和矩阵U及参数εi ＞0(i=1,2,3)使得

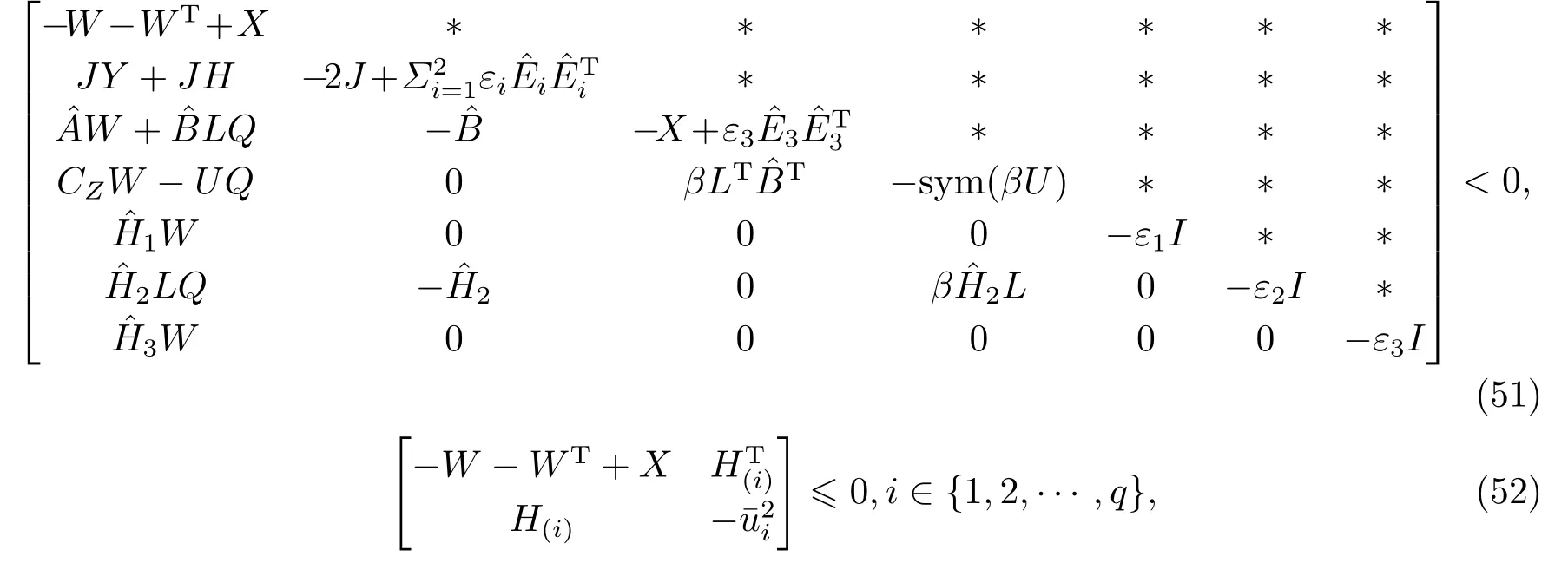
成立, 则闭环系统(47)在ε(P)内是渐近稳定的.其中输出反馈增益矩阵为K=LU-1, 控制输入为u(k)=KU-1Z(k).

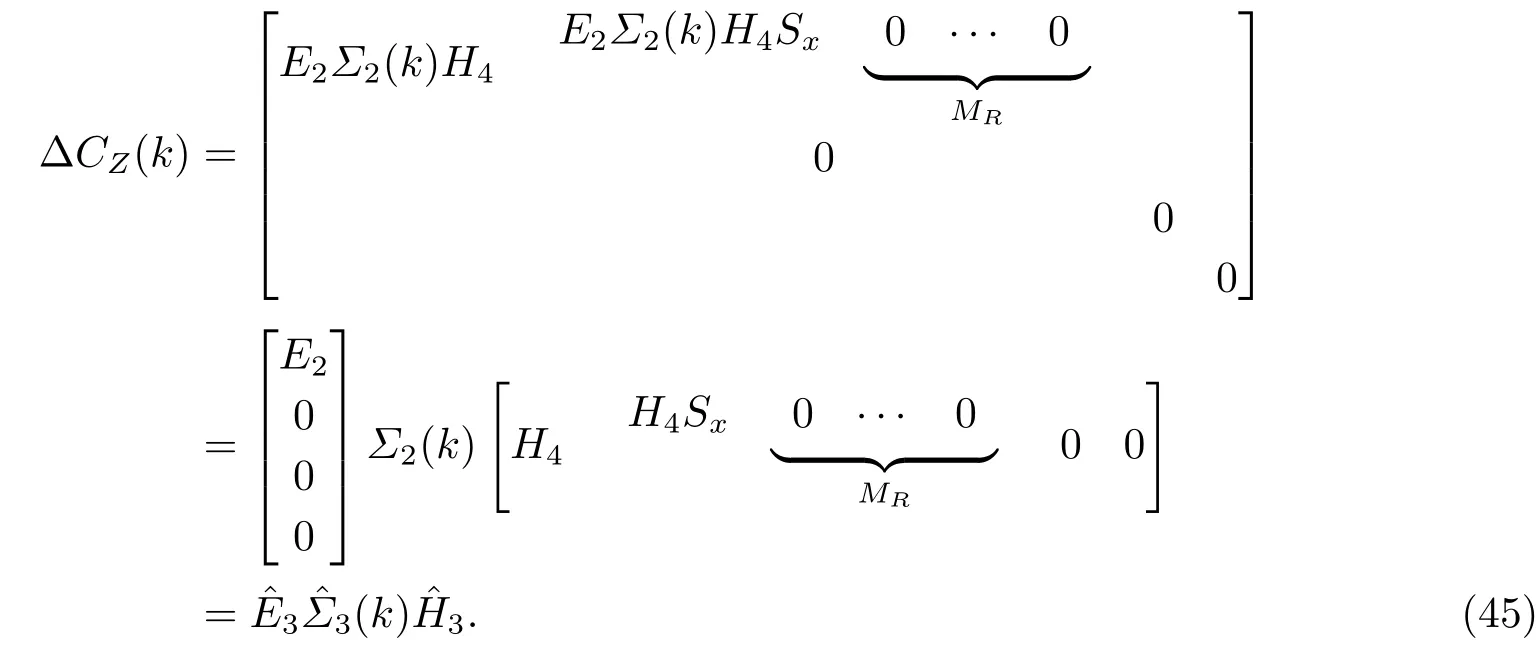
证同样, 为了叙述简捷, 用Ψ表示式(48)左边的矩阵.把Ψ的不确定部分分离出来,并结合式(21), (22)和(45)得到

其中

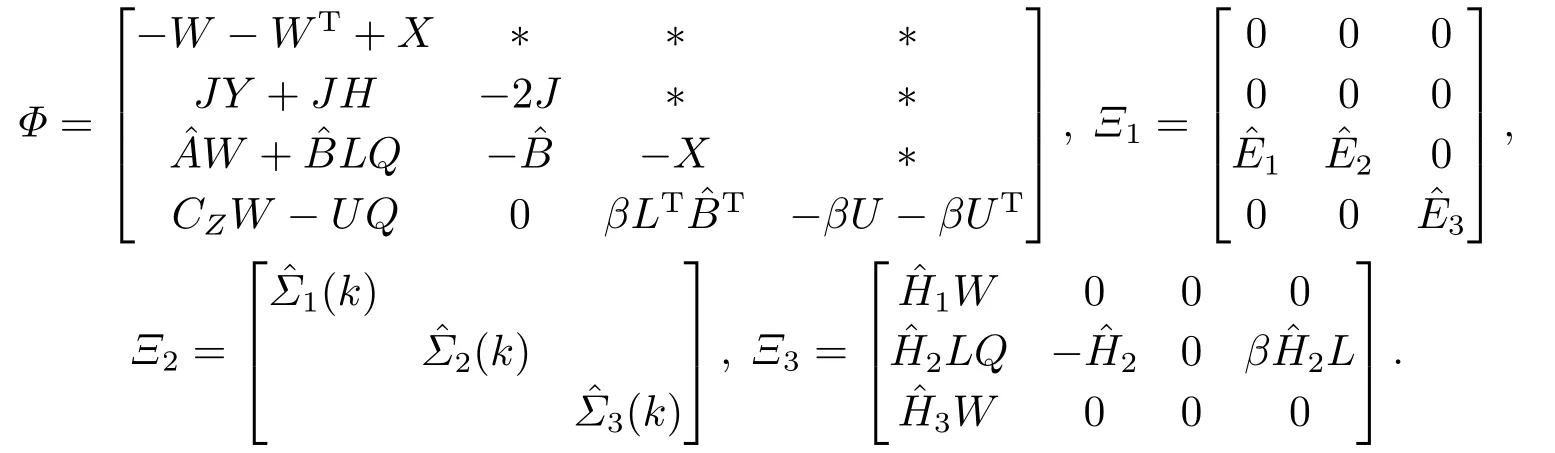
由式(23)可知ΞT2Ξ2≤I, 对式(50)左边后两项应用引理2, 令Λ=＞0,i=1,2,3,得

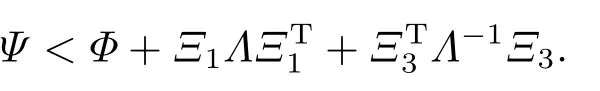
因此, 如果存在εi ＞0(i=1,2,3)使得

就有Ψ ＜0, 从而定理3的条件满足.根据定理3可知本定理成立.

按照Z(k)的定义, 对增益矩阵K分解

则式(46)可写为

可进一步改写为

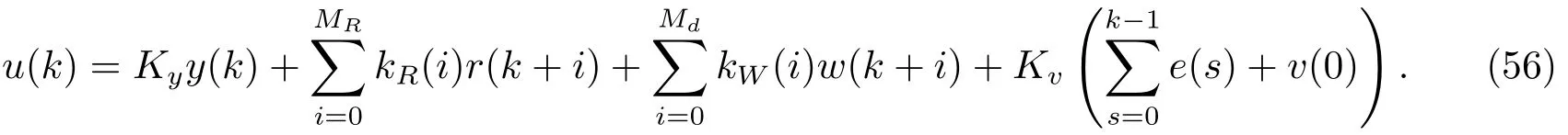
5.数值仿真

针对以下三种情况进行数值仿真: 1○Md=3、MR=8、MR=2；2○MR=2、Md=5、Md= 2连同没有预见的情况, 即MR=Md= 0进行比较.根据定理2, 得到反馈增益矩阵K=Y W-1.

当Md=3,MR=8时, 求得

当Md=3,MR=2时, 求得

当Md=MR=0求得

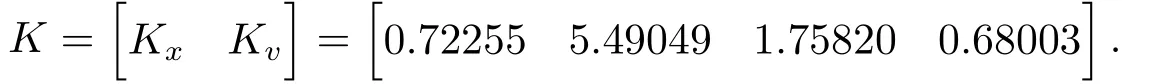
干扰信号取为

目标值信号取为

针对上述三种情况, 状态变量的初始条件取为x(0) = [0.1-0.1 0]T,= 1.经过验证(0)∈ε(P).图1给出了系统(1)的闭环系统的输出响应, 图2是跟踪误差.从图可以看出输出信号都能准确地跟踪目标值信号.但随着目标值预见步长的增加, 跟踪误差在减小, 调整时间在缩短且系统的输出能更快跟踪目标信号.

另外, 根据式(6), 可求得

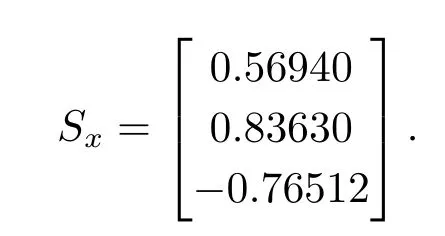
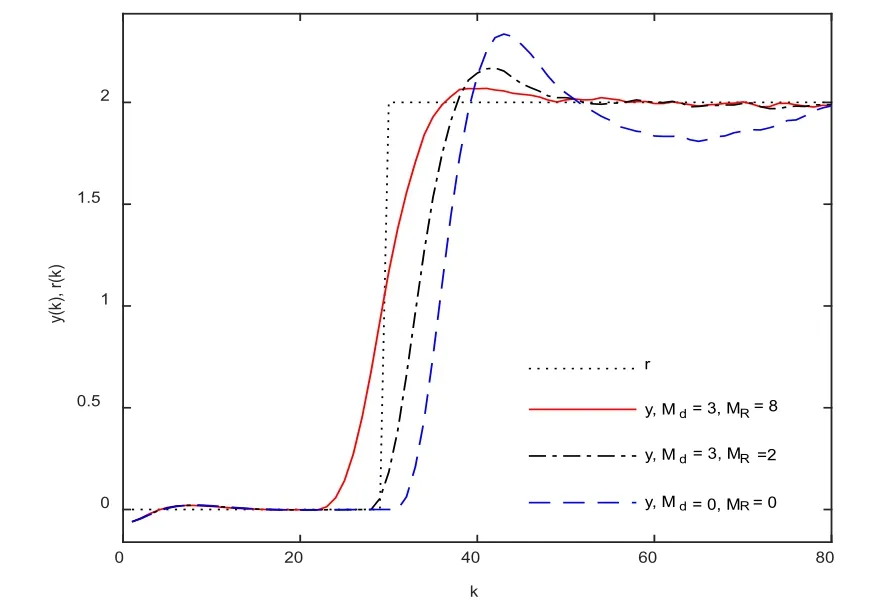
图1 Md不变、MR取不同值与无预见情形闭环系统的输出响应的比较

图2 Md不变、MR取不同值与无预见情形闭环系统的跟踪误差

图3 Md不变、MR取不同值与无预见情形闭环系统的控制输入

为了了解预见补偿项对u(k)的控制效果.这里给出um(k)随时间变化的曲线, 如图3所示.

我们对目标值信号和干扰信号的预见步数分别为MR=2,Md=2和MR=2,Md=5, 及目标值信号和干扰信号都没有预见即MR=Md= 0, 三种情况进行数值仿真.图4给出闭环系统的输出响应, 图5是跟踪误差, 图6是控制输入.从图4-6可看出, 当目标值信号预见步长相同的情形下(MR=2), 干扰预见步长的增加使得输出跟踪目标信号的超调量在减小, 且更好地抑制外部扰动所引发的振荡.虽然当干扰信号出现时, 为了削弱干扰的影响, 控制输入暂时随着预见步长的增加而有所增加, 但随后控制输入迅速减小.

图4 闭环系统的输出响应

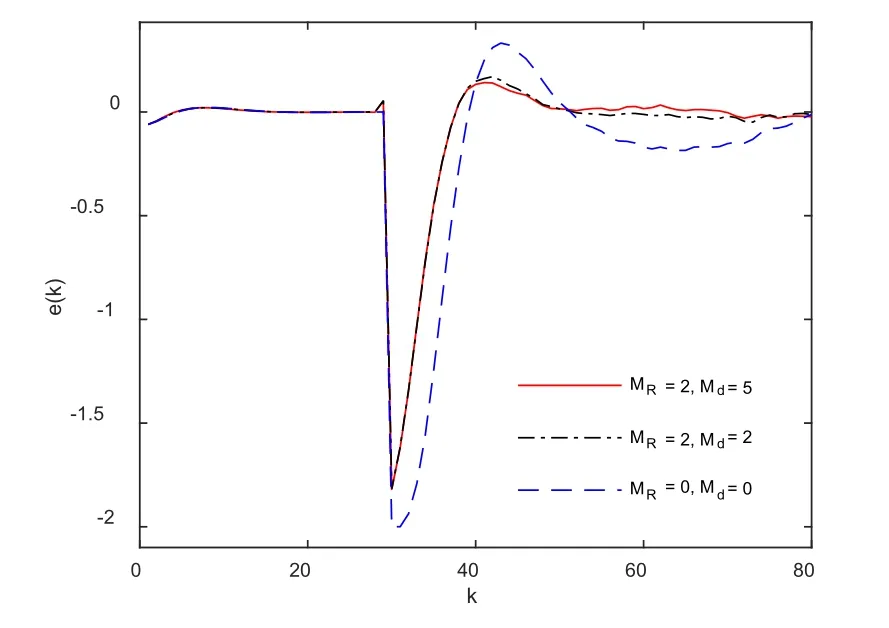
图5 闭环系统的跟踪误差

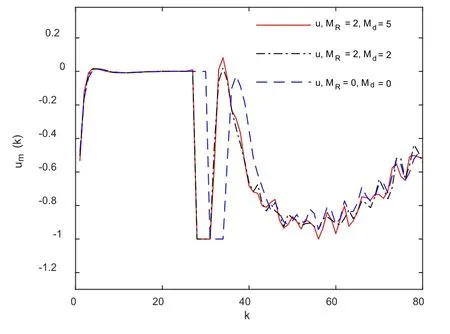
图6 闭环系统的控制输入

6.结束语

本文结合一种辅助方法和预见控制理论中误差系统的思想, 讨论了输入饱和不确定离散时间系统的鲁棒预见控制问题.首先通过引入辅助变量构造出扩大误差系统, 避免以往对输入饱和项和不确定项取差分的困难, 将原系统的预见跟踪问题转化为扩大误差系统的稳定性问题.最后结合Lapunov稳定性理论和LMI方法给出了预见控制器的设计方法.最后的仿真说明了本文控制器的有效性.