集优化问题的近似Benson真有效解及非线性刻画

杨兴宇, 黄斌, 徐义红

(南昌大学数学系, 江西 南昌 330031)

1.引言

集值优化是向量优化的一种推广, 近年来, 由于集值优化问题在数学金融、模糊优化、福利经济学等许多领域的应用, 它已成为应用数学中一个蓬勃发展的分支[1-7].向量准则和集合准则是求解集值优化问题的两个著名准则.向量准则只依赖于像集的单个元素, 而由Kuroiwa[8]提出的集合准则则依赖于像集的每一个元素, 因为它涉及到像集的直接比较.Kuroiwa等[9]引入了集合的六种序关系.后来, Jahn和Ha[10]定义了新的序关系, 并给出了一些性质.Karaman等[11]还在Minkowski差的基:上引入了偏序集合关系.

在实际应用中, 我们所建立的数学模型往往不够精确, 会忽略次要因素, 且算法通常生成近似解, 因此我们得到的解通常是近似解而不是精确解.Kutateladze[12]提出的近似解在最优化理论中起着十分重要的作用.文[13-15]中, 几位作者研究了向量优化问题近似解的不同概念.Dhingra和Lalitha[16]基于向量和集合准则方法, 引入了集值优化问题的近似弱有效解的若干概念.在集合逼近的情况下, 利用集合的上下拟序关系引入了两个近似弱有效解的概念,并进一步讨论了这些近似解的紧性和稳定性.Meenakshi Gupta[17]针对约束集优化问题, 基于Karaman等提出的集序关系, 定义了一个新的近似弱最小解的概念, 得到了最小解集闭性的充分条件; 利用Painlev-Kuratowski收敛性, 讨论了近似弱最小解集的稳定性问题.

本文拟借Minkowski差引进集优化问题的一类近似Benson真有效解的概念, 并利用非线性泛函建立最优化条件.

2.基础知识

设X、Y和Z为实赋范线性空间,C是Y中的闭凸点锥且int∅,D是Z中的点凸锥.用P(Y)表示Y的非空子集族.用B(0,ε)表示以原点为中心, 以ε为半径的开球.

设P和Q是P(Y)中任意集合.Minkowski差定义为

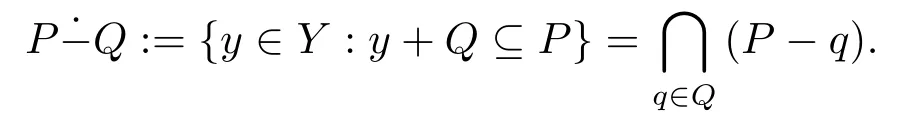
命题2.1[20]若P,Q ∈P(Y)且c ∈Y, 则

定义2.1[3]设元素x0∈X, 集值映射Ψ:X →2Y.

(i) 若对Y中任意包含Ψ(x0)的开集W, 都存在一个x0的邻域Nx0, 使得对于任意的x ∈Nx0,都有Ψ(x)⊆W, 则称Ψ在x0是上半连续的;

(ii) 若对于graphΨ中满足xn收敛于x0的每个序列(xn,yn), 都存在子序列(ynk)和y0∈Ψ(x0), 使得(ynk)收敛于y0, 则称Ψ在x0是紧的.

若映射Ψ在T上每一点都是上半连续(紧)的, 则称Ψ在T ⊆X上是上半连续的(紧)的.

命题2.2[3]设x0∈T, 且Ψ:X →2Y是集值映射.则Ψ在x0是紧的当且仅当Ψ(x0)是紧的,并且Ψ在x0是上半连续的.

3.近似Benson真有效解

考虑集值映射F:X →2Y和非空集合∅设对任意的x ∈X, 有F(x)∈P(Y).

设ε为非负实数,e ∈intC.考虑集优化问题

(PC) minF(x) s.t.x ∈T.

下面引入s-Benson真有效解和近似s-Benson真有效解的定义.

定义3.1设x0∈T,

(i)如果对于任意的x ∈T,都有clcone(C+F(x)F(x0))∩(-C)={0},则称x0是(PC)的s-Benson真有效解, s-Benson真有效解集记为s-Ben(F,T,C);

(ii) 如果对于任意的x ∈ T, 都有clcone(εe+C+F(x)F(x0))∩(-C) ={0}, 则称x0是(PC)的ε-s-Benson真有效解,ε-s-Benson真有效解集记为ε-s-Ben(F,T,C).

注3.1如果ε=0, 则ε-s-Benson真有效解变为s-Benson真有效解.

定理3.1对于任意的ε≥0, 有s-Ben(F,T,C)⊆ε-s-Ben(F,T,C).

证若ε=0, 则s-Ben(F,T,C)⊆ε-s-Ben(F,T,C)显然成立.

设ε ＞0, 且x0∈s-Ben(F,T,C).由定义知

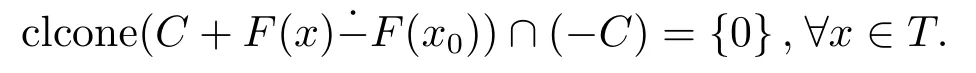
又因为e ∈intC, 所以

因此,

显然0∈clcone(εe+C+F(x)F(x0))∩(-C), 所以

得证.

因此,

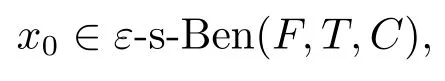
所以ε-s-Ben(F,T,C)是闭的.

下面举例说明定理3.2中F的开性和上半连续性不能去掉.

例3.2设ε=0.1,Y=R2,C=,e=(1,1),X=R,T=[0,2].

(i) 考虑F:T →2Y定义为

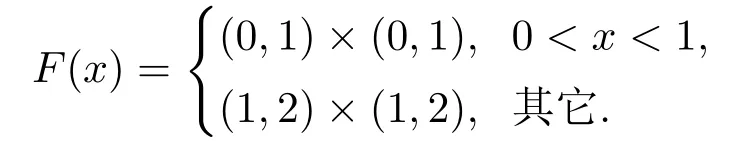
于是,T是闭的,F在T上是开值的, 但F在x= 0和x= 1处不是上半连续的.易求得ε-s-Ben(F,T,C)=(0,1), 不是闭的.

(ii) 考虑F:T →2Y定义为

于是,T是闭的,F在T上是上半连续的, 但F在T上不是开值的.易求得ε-s-Ben(F,T,C) ={0}∪(1,2], 不是闭的.

4.无约束优化的近似Benson真有效解的非线性刻画

接下来, 我们讨论无约束集优化问题的ε-s-Benson真有效解的非线性刻画.

也就是ξ(x1)≤ξ(x2).

下面举例解释上述定理.

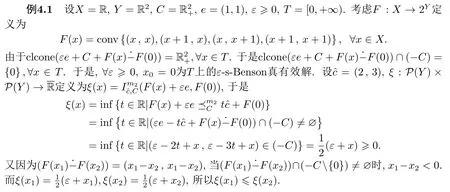
5.带约束优化的近似Benson真有效解的非线性刻画

接下来, 我们讨论带约束集优化问题的ε-s-Benson真有效解的非线性刻画.

6.结论

借助Minkowski差引进了一类Benson真有效解和近似Benson真有效解的概念, 讨论了它们之间的关系.当可行域是闭集且目标函数是上半连续且开值时, 证明了近似Benson真有效解集是闭的.给出了集优化问题取得ε-s-Benson真有效解的必要条件.特别地, 当ε= 0时得到s-Benson真有效解的若干刻画.