基于线框分析方法的建筑物主体模型智能构建

王贲文 臧玉府 黄奕舒

0 引言

三维建筑模型作为城市地信系统所有应用的基础，承担着城市语义信息管理和可视化表达的重要功能[1]，模型提供的位置、方向、结构等空间信息是实景三维建设、城市管理、城市规划、智能导航等应用的重要数据.另一方面，摄影测量和激光扫描技术是近年来快速发展的高精度空间信息获取技术，能够高效、精准地获取建筑物表面三维点云数据，是城市模型构建的重要数据源.因此研究基于三维点云稳健、准确地构建三维建筑模型具有重要意义[2].

迄今为止，国内外学者已对建筑物三维模型构建进行过大量研究.例如Zhou等[3]提出基于单目图像的三维构建方法，利用图像中的阴影推测出深度信息从而生成建筑模型，但该方法精度较差.为提高建模精度，Jung等[4]提出了模型-图像配准方法，该方法基于上下文的几何哈希算法实现单张图像与三维建筑模型的配准，将复杂的建筑模型视作简单建筑模型的集合，匹配地图中的建筑平面数据与航空图像实现三维重建.此外，Xiao 等[5]提出利用倾斜摄影的优势，通过同时处理二维影像与三维模型实现模型构建，有效地简化了模型并提高了稳健性，但该方法处理建筑物边界时精度仍显不足.随着空间数据获取技术的逐渐成熟，研究基于广义影像点云的建筑物模型重建方法得到了广泛关注[6].

建筑物的几何结构可有效地描述建筑物的模型尺度与结构信息[7].按照建筑物的结构体系划分，建筑物的几何结构可分为主体结构和细节结构，前者反映了建筑物的框架信息，可描述建筑物主要结构间的连接关系，是建筑物精细化语义建模的基础.主体结构的重建分为基于表面边界特征的分割和基于形状特征的分割.Wu等[8]应用基于骨架的分解方法，通过表面的聚类将模型分割为初始的模糊区域，然后在模糊区域里寻找更精确的分割边界，完成模型不同结构的分割.Yang等[9]提出了一种基于组件的3D形状无监督协同分割算法,输入模型预先划分为有意义的组件，通过高斯核函数与动态k均值聚类算法实现结构的划分.Aubry等[10]通过对模型点构建量子力学特征，通过特征进行聚类完成模型的分割.基于深度学习，Shu等[11]提出在过分割的基础上，以无监督与深度学习两种方式分别学习高级和低级特征，实现了不同结构的分割.Wang 等[12]设计了一种形状全卷积网络(Shape Fully Convolutional Networks,SFCN)，可以有效地学习和预测不同形状，通过对具有相似或不同特征的数据集测试，获得了不错的结构分割结果.不同于上述方法，孙轩等[7]采用基于体元的模型结构化分割方法，将三维模型体元化，通过模型表面与体元的求交运算、体元聚类等方式实现建筑物模型的主体结构提取，但是该方法需要复杂的求交运算与空间距离场的计算.

本文提出一种基于线框分析的建筑物主体模型构建方法，通过使用边界多边形表述建筑物不同高度的几何特征，构建建筑物的主体结构模型.本文构建的是建筑物主体结构的线框模型，相较于多面片建筑物模型，在一定程度上有效压缩了数据量，有利于城市大规模数据的处理与实际应用.本文方法还可以克服原始建筑物点云数据出现的缺失与噪声，稳健地处理不同的建筑物点云数据.

1 建筑物主体模型自动构建方法

由于城市场景复杂(如树木遮挡、过往车辆与行人干扰)，使得建筑物点云中常存在数据缺失、点密度差异大、噪声较多等问题，对建筑物三维模型构建方法提出了严重挑战.为了稳健提取建筑物特征，本文首先对原始数据进行滤波与归一化处理，保留建筑物特征，对不同高度进行特征提取，从而构建建筑物主体结构模型，主要分为以下4个步骤：

1)建筑物点云的滤波、归一化；

2)对不同高度点云进行直线提取、边界多边形规则化；

3)通过边界多边形分割出矩形框描述不同高度的结构特征；

4)通过不同高度矩形框的对比实现建筑物主体模型的完整构建，构建适用于不同建筑物的主体模型构建方法.

建筑物主体结构构建流程如图1所示.

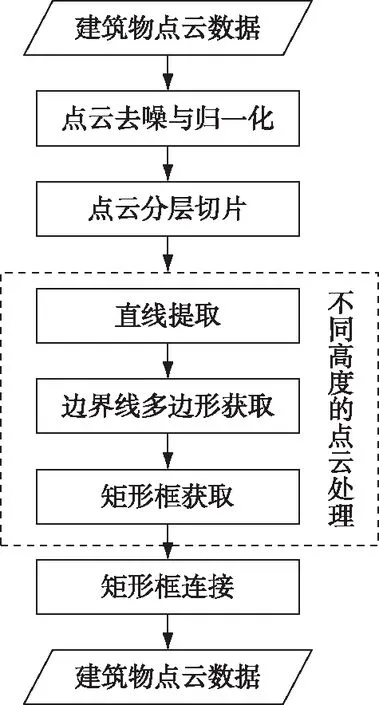
图1 建筑物主体结构构建流程Fig.1 Frame of building main structure construction

1.1 三维点云质量优化

在处理点云数据前，先对点云进行滤波处理去除离群点，以优化点云质量.本文采用基于统计学知识的噪声点探测方法[13]，在原始点P={P1,P2,…,Pn}中，Pi为其中任意一点，n为建筑物点的总数，统计其邻域点，计算Pi与邻域点间的平均距离，将平均距离小于阈值的点作为建筑物点.本文阈值设置为总体点云平均距离的3倍标准差.

为便于后续计算，本文对建筑物各点的z值进行归一化处理，如式(1)所示：

(1)

式中，Znorm为点Pi归一化后的z值，Zi为点Pi的原有z值，Zmax与Zmin分别为所有建筑物点在z轴方向上的最大值与最小值.

1.2 格网切片与降采样

在高度方向上建筑物结构、形状往往具有较大的差异，所以为精确地刻画建筑物的结构与形状，本文按高度切分多层次建筑物点云.为减弱建筑点云点密度差异、点云缺失、噪声多等因素的影响，本文对切片点云的格网采用降采样的方式处理.在x，y，z方向上构建的格网数Gx，Gy，Gz分别计算如下：

Gx=ceil((maxX-minX)/Gs),

Gy=ceil((maxY-minY)/Gs),

Gz=ceil((maxZ-minZ)/Gs),

(2)

式中，maxX，maxY，maxZ分别为各点在x，y，z方向上的最大值，minX，minY，minZ分别为各点在x，y，z方向上的最小值，Gs为格网的大小(本文取0.1 m)，ceil(·)为向上取整操作.计算每个点落在格网的位置，取格网中心点作为采样后的点，图2a为某层的点云降采样后示例图.

1.3 建筑物边界多边形层次化提取与规则化

为准确提取各层次下的建筑边界多边形，以描述建筑物该层形状特征，本文通过直线提取和边界多边形的规则化实现.基于降采样点云，采用最小二乘直线拟合算法提取直线特征.给定初始点Pi，通过拟合其邻域点大致方向为

Axi+Byi+Czi+D=0,

(3)

式中，xi，yi，zi为初始点Pi的坐标，A,B,C,D为拟合直线一般式的线参数.对点集中的其余点，聚类距离该线小于阈值范围内的点(本文阈值设置为0.25 m)，并再次采用最小二乘拟合，更新线参数，通过迭代运算，直至聚类的线上的点趋于稳定.直线聚类结果如图2b所示，其中不同的颜色代表不同的直线段.相较于图2a降采样后的点云，该层建筑物点云的线特征可以被正确地提取出来.

由于提取的线段间存在交叉、空缺等不规则现象，导致建筑物边界存在边界模糊、细节缺失以及连通性差等问题，无法直接对直线段进行连接处理以生成边界多边形.因此通过以下方式实现直线特征的规则化：选定最长的直线作为起始生长线，根据端点确定方向，生长方向为下一条直线点数多的直线段，判断下一条直线与生长线之间的关系(如垂直或平行关系)，规则化过程自动调整与文献[14]规则化方法类似.本文采取信任点数多的线段来进行规则化，如表1所示.表1中序号①和②表示生长线与下条线段垂直的情况，③～⑥表示平行的情况.边界多边形生长流程如图3所示，黑色线段为直线检测中未被检测出来的，但在规则化过程中生成的线段.

1.4 各层矩形基元提取与稳健连接

为实现建筑物上下层间的稳健连接，完整表述建筑物线框模型，在获取每层轮廓线之后，对边界多边形进行矩形基元的划分.如图4所示，假定图4a为竖直方向，图4b为水平方向.算法流程如下：

1)选择轮廓线的一个方向为矩形生长方向，图4中生长方向为竖直方向，对两个方向的直线进行排序，在竖直方向上选用图4a中①号线为生长线；

2)根据生长线，与同方向邻近的下一条线构成预定的矩形；

3)在水平方向上(图4b)进行矩形边与相交线的判定，图4b中①号线为矩形边，⑤号线为相交线，对矩形边水平①号线进行判断，相交于竖直线(图4a)①和②的上顶点，则生长线更新为I-I′(图4c中的L)，若不同时为上顶点或下顶点，生长线更新为I-I′ (图4d中的L)，边界更新为I-I′-C-D-E-F-G-H-I；

This work was financially supported by the National Natural Science Foundation of China (NSFC) (61675169, 61377055 and 11634010), the National Key R&D Program of China (2017YFA0303800), and the Fundamental Research Funds for the Central Universities (3102017zy021, 3102017HQZZ 022).

图2 切片点云直线提取结果Fig.2 Line extraction results of slice point clouds a.original slice point cloud;b.line extraction results

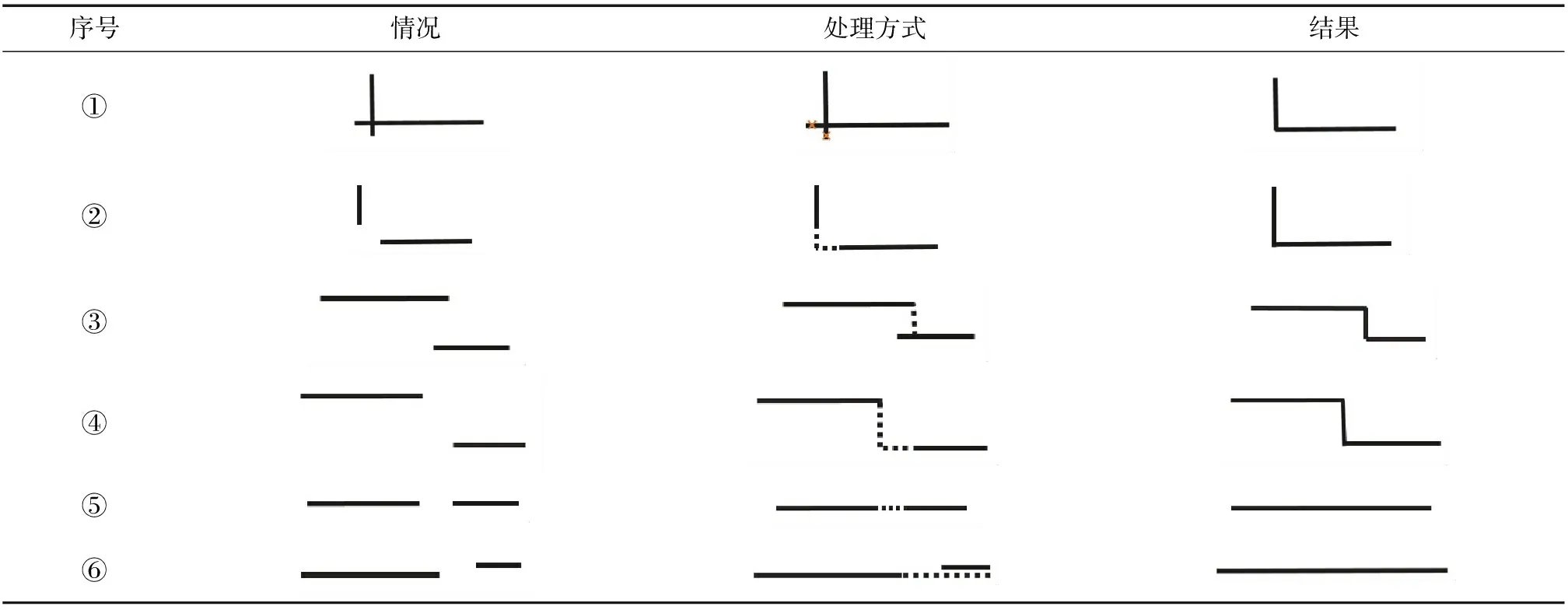
表1 几种边界多边形规则化处理方式[14]

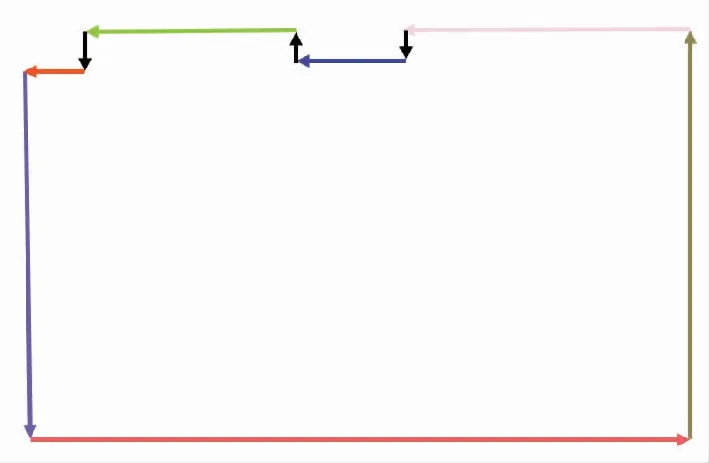
图3 建筑物切片点云轮廓线生长Fig.3 Growth of point cloud contour for building contour

4)重复2)和3)直至遍历所有的竖直线，获取当前高度的矩形.

在获取每层的矩形结果后，为了得到建筑物完整的线框模型，需要对获取的层矩形进行连接.考虑到原始建筑物点云可能存在缺失、边界模糊等问题，不同高度之间的矩形存在差异，因此在连接过程定义各层轮廓线的置信度值λ，计算如下：

图4 建筑物某一高度矩形生长Fig.4 Growth of building rectangular at a certain height

(4)

式中，ninlier为当前层处于轮廓线上的点，Nall为当前层的总点数，λ主要是判断当前高度边界多边形的可信度.另外，对于建筑物来说，一般较低层的层矩形面积较大，对于第i层的矩形面积Si，若其为底部某层，Si应略大于层矩形的平均面积Sa.因此，在线框模型生成时，若初始底部层的面积小于Sa，则先不生长成体，直至满足面积要求.伪代码如下：

层矩形连接算法∥输入:层信息,包括λ、层矩形、轮廓线及点for i←0 to n-1if Si≤Sa i←i+1elsek←i+1生成至当前层矩形体tCu,参考层矩形为当前层reRfor j←k to n-1 if (Sj-Sj-1) < 面积阈值 if (λj≤λj-1) 更新tCuelse更新tCu 更新参考层矩形reRelse AllC←tCu更新tCu与reR∥输出:线框模型(AllCu)

2 实验结果与分析

2.1 实验数据

本文采用三座建筑物原始点云数据如图5所示，其相关采集参数与数据信息如表2所示.三座建筑物形状复杂，参数与特点各不相同，适合验证本文算法的稳健性和有效性.

2.2 不同高度特征与建模结果

图6为三座建筑物的某一层的点云数据直线拟合结果，可以看出三座建筑物点云数据存在部分门窗缺失、树木行人遮挡造成的点云缺失与噪声现象.图7a汉口路建筑边界多边形克服了原始点云中缺失(图7a中上方的绿色线与紫色)与噪声(图7a中下方的蓝色线两端)，完整构建了该层的边界多边形.由图6b与图7b可以看出，武大教学楼点云因为在规则化过程中选择了长直线段，导致上部一小部分出现缺失现象，但对该层的边界多边形影响不大.图6c中，武大宿舍楼连接处出现大量数据缺失，在图7c中，规则化过程中克服了背部点云数据缺失的现象.

图5 三座建筑物原始点云Fig.5 Original point cloud of three buildings

表2 三座建筑物点云详细参数与特点

图6 三座建筑物某一层的点云直线拟合结果Fig.6 Line fitting results of point cloud for three buildings on a certain floor

图7 三座建筑物某一层的边界多边形Fig.7 Boundary polygons of three buildings

图8为三座建筑物的某一层的结构特征，三座建筑物均通过规则的边界多边形正确获取了当前层的矩形结构，由图8a与图6a可以看出，图6a中的8条被检测出的直线段为当前层的直线特征，不能整体全面地描述当前层的结构，图8a仅使用4个规则的矩形，完整正确地反映了当前层的结构.通过对比图6b与图8b，图6b上部组成建筑物的阳台较多，直线段多且有空缺，图8b中使用了4个矩形框描述了当前层的主要结构.通过对比图6c与图8c，图6c显示该层武大宿舍楼点云缺失、边界模糊，该层结构不易判断，图8c则以6个矩形框正确完整地表述出来.

图9为三座建筑物的线框模型，图10为建筑物主体结构的线框模型构建结果，通过对比图5、图9与图10，可以看出由于建筑不同高度点云数据质量不一致，在构建线框模型时，部分建筑物出现一些多余点云以矩形框的形式表示出来(图9a汉口路线框模型右上部)；武大教学楼线框模型显示不同高度部分缺失的数据对本实验有一定影响(图9b武大教学楼中间绿色部分)；而武大宿舍楼结构较为简单，使用规则的矩形框可以完整地表示出来，但阳台在规则化过程中被略去.总体来说，三座建筑的主体结构特征以多组矩形框的形式被正确表示出来.图10为三座建筑物主体结构线框模型渲染后的结果.

2.3 建筑物主体模型评估

评价指标为完整率(MComp)、正确率(MCorr)以及精度(MAcc)，缓冲区大小b与截止距离(单位：cm)的范围为1～10 cm.完整率表示建筑物线框模型表述真实测量值的完整程度，正确率表示建筑物线框模型描述真实测量值的正确程度，这两个指标[15]定义如下:

图8 三座建筑物某一层矩形结构Fig.8 Rectangular structures of three buildings on a certain floor

图9 三座建筑物的线框模型Fig.9 Wireframe models of three buildings

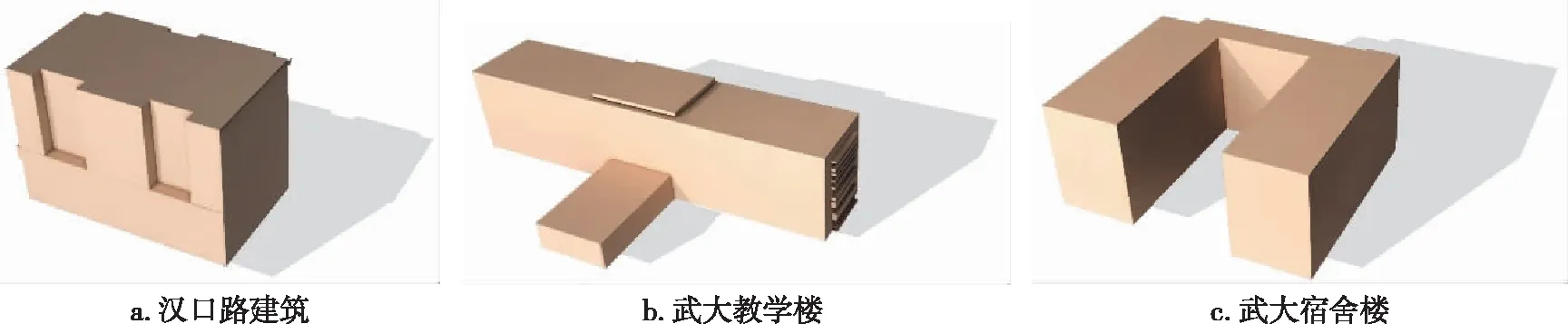
图10 三座建筑物模型渲染结果Fig.10 Output render results of three buildings

(5)

(6)

式中，b(·)表示真实测量值Rj周围缓冲区的大小，n和m分别表示构建的线框模型S与真实测量值R的表面个数，这里|·|表示区域的表面面积，ρ表示的是构建模型的外表面与对应真实测量值表面上的正射投影.

对于精度测量，描述的是构建的模型与真实测量值之间的欧氏距离，定义为点云至构建模型表面的最近距离：

(7)

精度评估结果如图11所示.

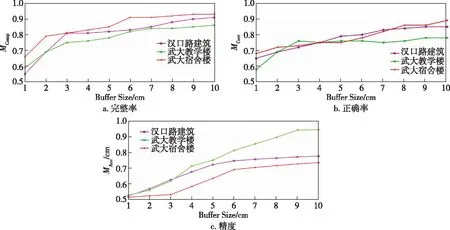
图11 模型质量评估Fig.11 Model performance assessment

由图11可知，汉口路建筑与武大宿舍楼完整率均超过90%，正确率大于85%，精度约为6 cm，而武大教学楼为两座建筑组成的建筑物，在完整率与正确率以及精度方面表现略差.三座建筑物在精度评定方面总体上都满足要求，表明本文算法构建建筑物主体结构模型可以取得较好的结果.

为验证本文方法的稳健性，对汉口路建筑原始点云添加高斯噪声，结果如图12所示.σ表示的是正态分布的标准方差，σ值的大小表示噪声点与原始建筑物点云的偏离程度.图12中，随着不同程度噪声的添加，原始建模结果变化较小.在构建建筑物主体模型时，本文选取建筑物的边界多边形来近似表述建筑物几何特征，尽可能表述不同高度的建筑物结构，在不同高度的对比与连接时起到了一定的优化作用，因此不同程度的噪声对本文结构影响较小.总体而言，本文提出的建筑物主体结构模型构建方法具有较好的稳健性.

3 结论与展望

图12 不同噪声水平下汉口路建筑的重建结果Fig.12 Reconstruction results of Hankou Road building under different noise levels

本文提出了基于线框分析方法的建筑物主体模型构建方法，在提取建筑物多层次的几何特征基础上，构建出与建筑物真实性接近的主体结构的线框模型，并通过三组典型的建筑物点云数据对本文的方法有效性进行了验证.实验结果表明本文方法能够通过规则化解决建筑物点云存在的缺失与点密度差异的问题，使建筑物模型的边界多边形尽可能与真实建筑物点云重合.在构建建筑物整体模型时，通过置信度提升了建筑物主体模型构建的稳健性.本文算法可以真实地保留建筑物几何结构，并且可以稳健适应多种形态建筑物，以数据量较少的线框模型表述了建筑物的主体结构，实现了建筑物的主体结构的高精度重建.但是在建筑物屋顶，以及建筑物一些细节(如阳台)上表现不够全面，后续工作会对此问题进行改进.