基于改进双阶段注意力机制的降水智能预报

戈苗苗 陆振宇 梁邵阳 夏英茹

0 引言

降水实时预报是指在很短的时间内对区域降水进行分析和预报,可为管理决策提供及时有效的环境信息,防止灾害的发生.现阶段天气预报主要依靠数值模式预报[1],预报员首先通过模式产品进行数据分析,然后根据自己多年的预报经验进行模式订正,但是这需要花费大量时间和成本对预报员进行培养.由于降水影响因素比较特殊,依靠模式预报很难抓取降水与环境要素之间的联系[2].李启芬等[3]通过选取预报因子,建立了夏季降水和气温预报动力统计混合模型,然而,模型订正效果在不同地区有明显的差异．降水量预测需要一种启发式的方法,这是典型的数值天气预报和统计学习方法所不能解决的,而机器学习、深度学习的迅速发展有效地弥补了数值预报的缺陷.任海青[4]利用灰度预测模型构建了预报模型,程敏等[5]基于时间序列模型ARIMA 对区域降水进行建模,构建了当地降水预报模型,张帅等[6]构建了递归神经网络的降水预报模型,上述模型在降雨量预测任务上取得了不错的结果,但因降雨形成因素具有动态性和非线性特性,仅依靠线性外推技术,是无法根据历史数据捕捉其繁衍趋势的.临近预报的研究领域涉及大量数据,基于序列的深层神经网络缺少非线性关系,在降水预报订正中效果欠佳.双阶段注意力机制网络是由Qin等[7]提出的一种多变量时间序列神经网络,它能长时间捕获时间序列的长期依赖性,改善模型的预测效果．本文所使用的降雨数据由与降雨量关系密切的环境因子组成,和双阶段注意机制网络的输入变量有着相似的结构.

本文基于双阶段注意力机制网络进行了一定修改：首先在第一阶段输入注意力机制中引入目标序列,通过连续三层注意力机制提取稳定的权重,让网络稳定抓取降雨环境因子的空间关系;其次,在网络输入阶段映射到编码阶段中,通过加入形变LSTM[8]缓解循环神经网络长时间记忆流失问题,进一步提高模型预报性能.

1 研究区数据及处理

广东省以亚热带季风气候为主,全境地势北高南低,北部、东北部和西部都有较高山脉,中部和南部沿海地区多为低丘、台地或平原．广东省海拔分布如图1所示.南部城市平均海拔较低,其中江门、阳江等临海城市受海洋气团的影响,普遍吹偏南风,从而带来了丰沛的雨水.6月是广东前汛期的降雨高峰期,而每年的6—10 月又是热带气旋影响广东的主要时段,各地出现暴雨的次数较多.如图2所示,临海城市普遍年平均降雨量相对北部城市而言较高,海拔高度、温度分布、风向等气象环境因素对不同地区降雨有着显著影响.

由于自动站设备老化或极端雷击等因素造成观测数据出现缺失、异常值的情况,在实验前,必须对脏数据进行去噪,过滤掉异常值.盒须图定义了识别异常值的标准:异常值一般为小于QL-1.5RIQ或大于QU+1.5RIQ的值.QL为下四分位数,QU为上四分位数,RIQ为四分位数间距,是上四分位数与下四分位数的差值.

由盒须图识别出的异常值,直接删除容易丢失众多隐藏在上下文数据中的信息,削弱数据之间的时间相关性.本文将异常值作为缺失值,利用缺失值的解决方案进行插值.常用的数据插补方法大致有:众数插补、最近邻插补、回归方法、插值法.由于降雨量数据前后关系紧密,使用众数、中位数等插补法插值的数据只能单一解决缺失值问题,并不能平滑数据,因此本文对缺失值前后的数据进行拉格朗日插值[9],其公式定义如下:

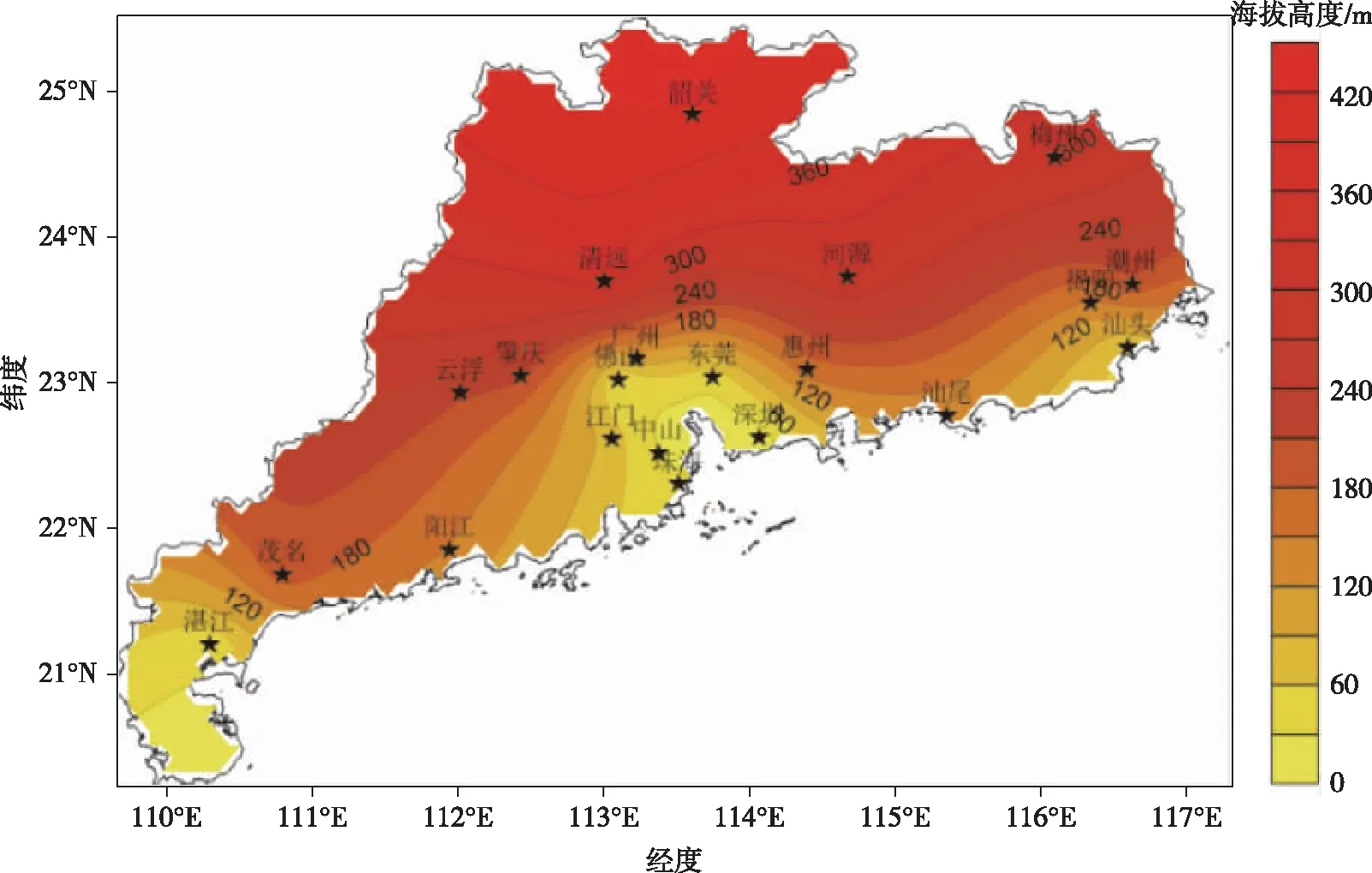
图1 广东省海拔分布Fig.1 Altitude distribution map of Guangdong province

图2 广东省平均年降水量分布Fig.2 Annual average precipitation distribution of Guangdong province

y=a0+a1x+a2x2+…+an-1xn-1,

(1)

(2)

式(1)为已知平面上n个点形成的n-1次多项式,式(2)为将n个点的坐标代入多项式函数,让缺失值对应的点x插值多项式,得到缺失值的近似值L(x).

对数据进行质量分析能有效剔除噪声数据,得到更加合理的观测资料,但这些数据并不能直接输入模型．气象台的观测特征较多,数据未经处理容易造成特征冗余的现象．因此,本文引入统计学方法[10]来研究变量之间的关系密切程度.

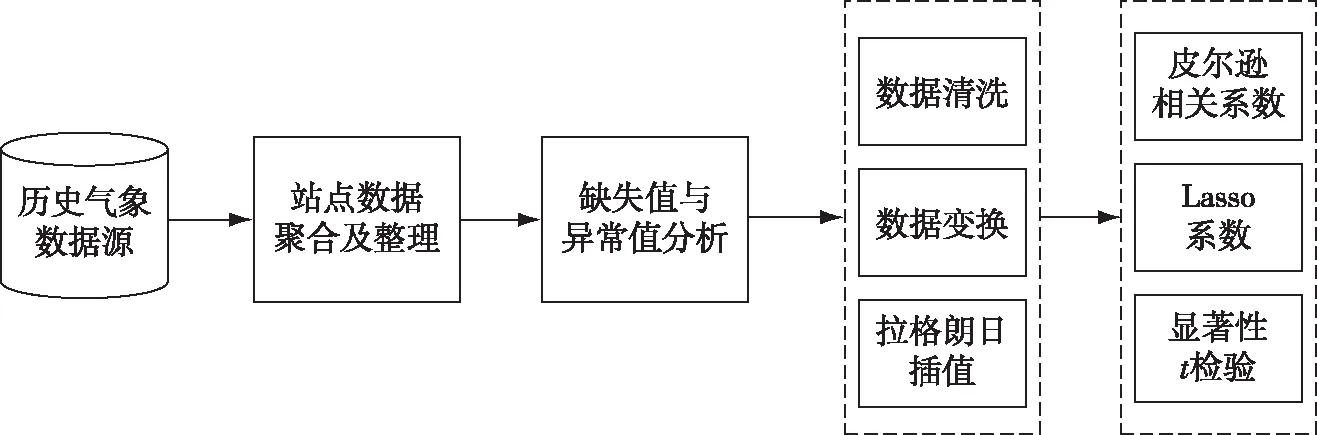
图3 数据预处理流程Fig.3 Data preprocessing flowchart

Lasso 变量选择具有稳定性,变量选取较为准确,其公式定义如下:

(3)

其中xij为矩阵中对应位置的值,yi为目标变量对应值,β为回归系数向量,λ为非负正则参数．通过选择合适的λ对模型进行调整,可以减少与因变量关系小的系数,同时对变量进行显著性检验,证明变量之间的相关性不是偶然因素导致的.实验中算法寻得最优λ为0.01．表1展示了部分Lasso变量选择和显著性检验结果.

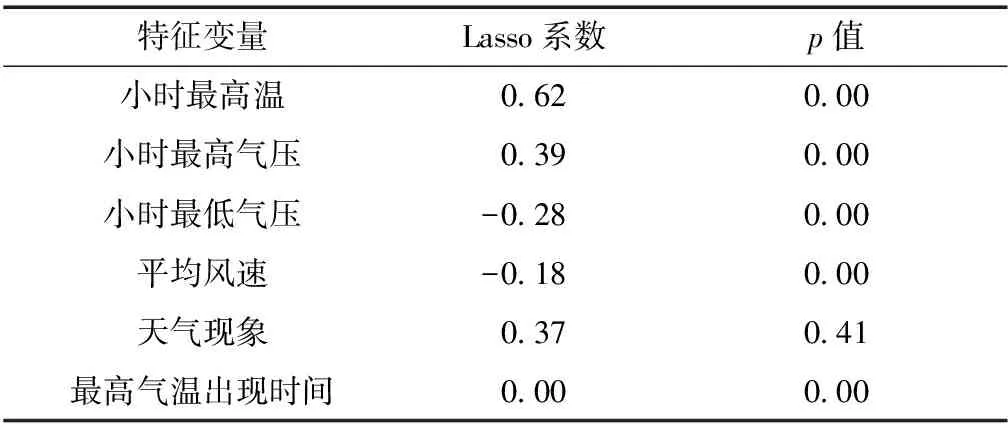
表1 Lasso变量选择系数及显著性检验

由表1看出:最高气温出现时间相关系数为0,同时p值小于0.05,说明该因素对降水量是不相关的,可视为无关因素;小时最高温、小时最高压等影响因子与小时降水量之间有着很强的相关性且p值小于0.05,说明这些因素是相关的;天气现象相关系数表现出弱相关性,但p值大于0.05,说明两个因素的高相关性可能是偶然因素导致的.

皮尔逊相关系数可以分析目标与变量之间的线性相关程度,其计算公式如下:

(4)

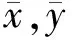
2 模型原理

2.1 形变长短时记忆神经网络

循环神经网络(RNN)被设计成可以利用历史的信息来辅助当下的判断,但是RNN主要依靠最后的输入信号来决策最后的结果,更早之前的输入信号会随着时间的推移被忽略,所以RNN在长期依赖问题上显得差强人意.长短时记忆神经网络(LSTM)的出现解决了这一难题,它主要在网络结构中新增了一个判别器,这个判别器的结构被称为“细胞”(cell).每个cell中包含三个门结构,依次为输入门、遗忘门和输出门.网络计算公式如下:

ft=σ(Wf·[ht-1,xt]+bf),

(5)

it=σ(Wi·[ht-1,xt]+bi),

(6)

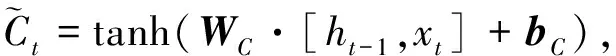
(7)

(8)

Ot=σ(WO·[ht-1,xt]+bO),

(9)

ht=Ottanh(Ct),

(10)

式中:ft,it,Ct,Ot分别为遗忘、输入、记忆细胞和输出门，Wf,Wi,WC,WO为相应权重矩阵，bf,bi,bC,bO为相应偏置向量.

LSTM通过加入输入、遗忘、输出门的方式,可以缓解梯度消失和信息遗忘问题.但是,在LSTM计算公式中,当前时刻输入xt和隐藏状态ht-1是没有关联的,而形变LSTM则在现有LSTM计算之前,通过门机制让输入xt和隐藏状态ht-1进行充分交互,得到新的输入和新的隐藏状态,这样两者能互相关联,达到增强上下信息联系的目的[8].具体公式如下:

(11)

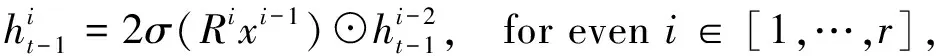
(12)

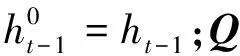
图4 Mogrifier LSTM交互示意Fig.4 Schematic of Mogrifier LSTM interaction

对于给定的序列信息{x1,x2,…,xt-1,xt},xi∈Rn,定义激活函数(形变LSTM)为F,则能计算每个时间步ht=F(ht-1,xt).

2.2 输入注意力机制

目前,注意力机制广泛应用于深度学习,在自然语言处理中,传统RNN注意力机制[14]通常在隐藏层信息中选择对结果有重要影响的时间步,而忽略了输入序列之间的影响.因此本文先对输入序列进行自适应选取,与双阶段注意力机制不同的是,本文在其第一阶段注意力中引入目标序列y和加深注意力模块层数得到一个稳定的输出权重,用来提取输入序列和目标序列的空间相关性,称该模块为深度输入注意力机制,结构如图5所示.

图5 深度输入注意力机制示意Fig.5 Schematic of deep input attention mechanism

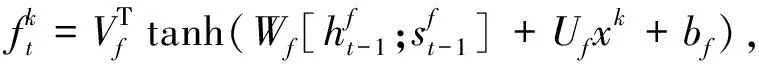
(13)

(14)

(15)

(16)

(17)

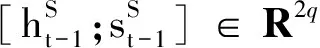
(18)

(19)

(20)

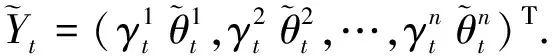
(21)

2.3 时间注意力机制

图6 时间注意力机制Fig.6 Time attention mechanism

(22)

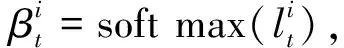
(23)

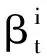
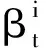
(24)

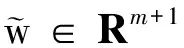
(25)

(26)

Wy∈Rp(p+q),by∈Rp,[dt;ct]∈Rp+q.

2.4 基于双阶段注意力机制的降水量智能预报

首先获取预处理的气象环境因子逐时实况资料,其次将ECMWF模式资料处理成对应站点数据,并对数据进行集成和归一化处理,再次将集成的预报因子输入到本文构建的改进双阶段注意力机制模型(DeepAMogLSTM)中进行训练、调优,优化模型效果,选取最优超参进行降水预报,最后进行数值检验和时空分布检验.

3 实验结果及分析

3.1 实验评价指标

本文选择回归任务中的均方根误差(RMSE,量值记为ηRMSE)、平均绝对误差(MAE,量值记为ηMAE)和决定系数(R2)评价指标对模型进行数值检验.RMSE是均方误差的平方根,通常代表预测值的离散程度,即标准误差,ηRMSE越小,结果拟合越好;MAE是平均绝对误差，由于预测误差有正有负,MAE能防止预测误差正负抵消,可以更好地反映预测值误差的实际情况;R2反映观测值与预测值的拟合优度,其数值越靠近1,拟合程度越好.它们定义分别如下:

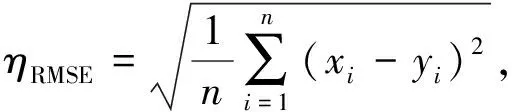
(27)

(28)

(29)

3.2 实验结果分析

3.2.1 降水预报数值检验

为验证模型在多因素降水预测上的有效性,本文对广东省沿海城市降水量数据进行网络评估,该数据经过上文相关预处理步骤,提升了数据质量.并以湛江市3 h累计降水量测试数据为例,图7、图8给出了本文模型降水量预报数值与其余方法(AR、SVR[15]、LSTM[16]、LSTnet[17]、DARNN[7])降水量预报数值的对比结果,预报时效分别为1 h和2 h,实验中对累计降水量不大于0.1 mm的数据进行了清零处理.

图7 各模型下1 h降水量预报值Fig.7 The 1 h precipitation forecasted by different models

图8 各模型下2 h降水量预报值Fig.8 The 2 h precipitation forecasted by different models

不难发现,AR线性模型作为时间序列算法之一,在时间序列问题的处理上有一定优势,但缺少非线性因素的影响,容易出现过大的峰值.SVR支持向量回归模型采用线性核函数做回归预测,但是在传统的多变量方法中,冗余的信息容易导致模型过拟合问题.作为近些年比较热门的深度学习网络LSTM和LSTnet能有效利用其长时间的记忆性能,取得更好的结果,但这两种方法更多的是关注时间相关性,没有考虑空间相关性.DARNN模型与单一的LSTM和LSTnet相比拟合更好,但本文提出的算法(DeepAMogLSTM)在曲线趋势上更加拟合,它能有效缓解单注意力机制权重变化分散的问题,通过第一阶段连续三层注意力机制提取平稳的权重,以更好地表示输入与目标序列的空间相关性.

为直观检验本模型在降水量预报上的性能,表2给出了各算法在测试集上的误差对比结果.

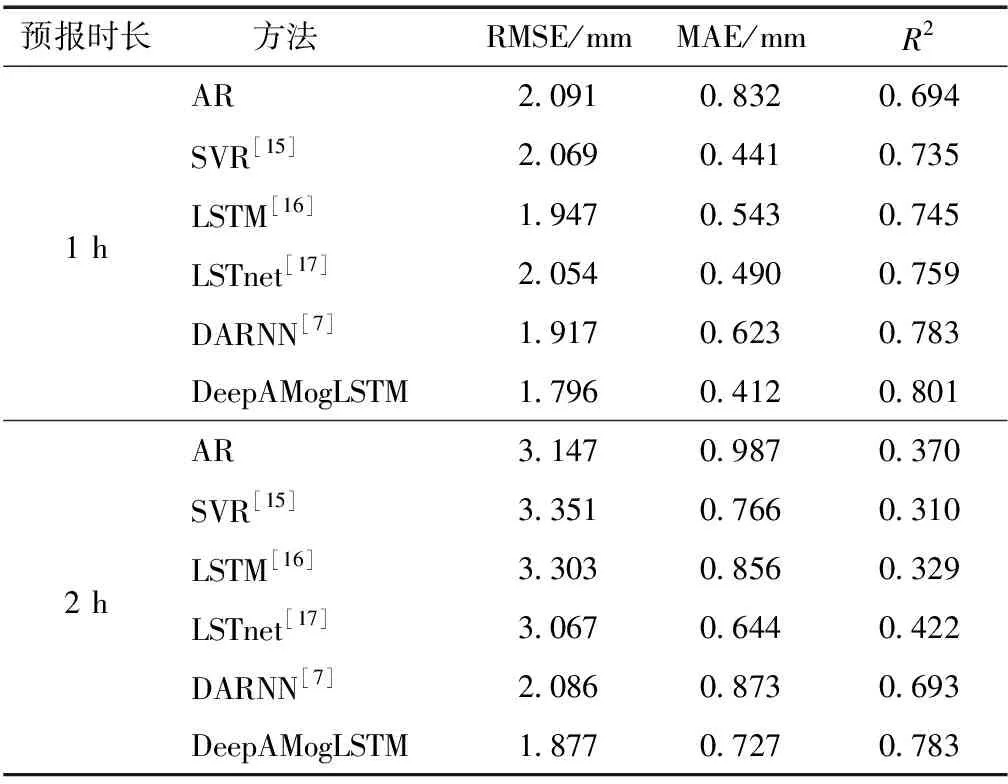
表2 六种预测方法的评价指标

表2结果表明,本文提出的模型在各评价指标上都有较好的成绩.当预报时长为1 h,模型的RMSE为1.796 mm,MAE为0.412 mm,R2为0.801;当预报时长为2 h,模型的RMSE为1.877 mm,MAE为0.727 mm,R2为0.783,其误差指数低于其他模型.

为验证改进模块在降水数据集上的影响结果,对DARNN的两个改动模块进行消融实验,主要结果如表3(模块1是改进第一阶段输入注意力机制,简称DeepA,模块2是加入形变LSTM,简称MogLSTM)所示．

表3 各模块实验评价指标对比

相较于DARNN,加入其余模块后预测效果都有小幅提升,其中加入输入注意力机制模块的改动对实验结果提升较大,加入形变LSTM后,模型能取得更优的结果.

3.2.2 降水预报空间分布分析

每年的夏季都是全国降雨高峰期,出现暴雨天气次数较多.本节以广东省2019年7月31日18时降水为例,对累计降水量进行空间预报分析.图9a—f和g—l分别是各模型预测广东省未来1 h和2 h累计降水量的空间分布,图10表示的是对应时间广东省观测资料的降水量空间分布.由于克里金插值法考虑了空间属性的变异分布,它可以有效剔除由于空间采样不均匀造成的误差,使结果更加贴合真实情况,所以作图过程中使用克里金插值法对广东省的降水预报空间分布进行插值.

由图10观测资料降水空间分布来看,广东省各城市降雨状态有明显分层,沿海城市(汕头、湛江等临海城市)累计降雨量多于西北山地地区,西北地区可能因为山地海拔高等原因,降水趋势往东北方向扩散.由图9可知,各模型整体预测累计降雨量空间分布状态是趋向于真实降雨空间分布的,其中DeepAMogLSTM和DARNN的降雨空间预报结果相对其余的降雨空间预报而言更符合实际情况,部分线性模型出现较高峰值,预报订正效果较差.由图9e—f和k—l可知,本文模型的降雨空间预报结果相对而言更拟合实际,从而间接反映加强输入注意力机制的空间特征提取能力对模型降水预报的订正十分有效.

4 结论

本文以降雨量预测为例,根据Lasso系数、显著性t检验和皮尔逊相关系数,筛选气象环境因子,并对部分缺失的特征数据进行插值填补.针对降水因素非线性关系复杂,预测较难的问题,提出一种改进双阶段注意力机制网络模型,并对该模型的性能进行数值检验和时空分布检验.通过实验分析得到如下结论:

1)本文对双阶段注意力机制模型进行了改进,相比DARNN与其余模型而言,DeepAMogLSTM模型在降水预报上的RMSE与MAE都取得了更好的结果.其中,模型预报时长1 h的均方根误差为1.796 mm,平均绝对误差为0.412 mm,拟合优度为0.801,模型预报时长2 h的均方根误差为1.877 mm,平均绝对误差位0.727 mm,拟合优度为0.783.

图9 2019-07-31 18:00各模型降水量预报空间分布 a—f.预测1 h累计降水量;g—l.预测2 h累计降水量;a,g.AR模型预报;b,h.SVR模型预报;c,i.LSTM预报; d,j.LSTnet模型预报;e,k.DARNN模型预报;f,l.DeepAMogLSTM模型预报Fig.9 Spatial distribution of precipitation forecast at 18:00 on July 31,2019, a-f.the 1 h cumulative precipitation;g-l.the 2 h cumulative precipitation;a,g.AR model;b,h.SVR model; c,i.LSTM forecast;d,j.LSTnet forecast;e,k.DARNN model;f,l.the proposed DeepAMogLSTM model

图10 2019-07-31 18:00(a),2019-07-31 19:00(b)观测资料日降水量空间分布Fig.10 Spatial distribution of daily precipitation observed at 18:00 (a) and 19:00 (b) on July 31,2019

2)以广东省2019年夏季各市降水空间预报为例,本文模型降水空间预报分布更拟合实际降水空间分布,局部分布相对其余模型而言更具优势.