改进支持向量机分类方法及其在原发性肝癌筛查中的应用

曹国刚， 李梦雪， 陈 颖， 曹 聪，王孜怡， 房 萌， 高春芳， 刘云翔

1.上海应用技术大学计算机科学与信息工程学院，上海201418

2.上海东方肝胆外科医院实验诊断科, 上海200438

原发性肝癌（primary liver cancer, PLC）的发病率在全球常见恶性肿瘤中居第5 位，其致死率高居第3 位。临床上约有2/3 的肝癌患者初诊时已属中晚期，错过了治疗时机[1-3].肝癌的早期发现、早期诊断、早期治疗是患者获得长期生存的主要途径。近年来，医疗数据与人工智能的不断发展为PLC 早期筛查提供了有力保障。其中，基于图像的人工智能方法[4]在肝癌识别和预测的应用中比较常见，例如文献[5] 基于肝脏多模态图像，利用支持向量机，识别肝脏肿瘤的良性与恶性，最终分类精度为92.31%。而且，还有学者利用生物技术指定肿瘤标志物，使用统计学方法进行肝癌患者和健康人群的识别，其中：文献[6] 的接收者操作特征曲线下面积（area under receiver operation characteristic（ROC）curve, AUC）值为0.96，敏感性为83.3%，特异性为93.3%；文献[7] 的AUC 值为0.94。基于临床数据的癌症筛查方法具有对患者友好、易于取样、价格便宜、易与算法结合的特点，尽管它的筛查性能不如医疗影像和病例检查，但仍然是癌症筛查领域备受期待的研究热点。例如，在临床检验诊断领域，学者利用了患者的性别、年龄等多项检测指标数值建立多参数诊断模型。文献[8] 诊断肝纤维化的AUC 值均超过0.70，个别达到0.80；文献[9] 预测显著纤维化和肝硬化的AUC 值分别为0.80和0.89；文献[10] 用于预测缺铁性贫血，诊断正确率超过90%。同时，文献[11-12] 将多参数模型在诊断肝癌、肝纤维化方面进行了探索，发现通过合理使用临床检验数据可以提升预测结果。

基于数据驱动的机器学习方法是目前人工智能领域广泛使用的手段，该方法通过研究现有数据的规律对未知数据进行预测。支持向量机（support vector machine, SVM）是20 世纪90年代中期发展起来的一种机器学习方法，具有深厚的数学基础以及突出的学习性能，在很多领域都得到了成功的应用，如人脸识别[13]、手写数字识别[14]、图像分割[15]及机器翻译[16]等。为了进一步提高其性能，需要对其参数进行优化。传统的优化方法有网格法、随机搜索法、梯度下降法等；另外遗传算法、粒子群算法等演化计算方法也可用来加速优化过程[17]。

本文基于临床常规检验指标数据，利用SVM 在解决小样本、非线性、高维空间模式识别问题中的独特优势，建立PLC 早期筛查模型，在训练过程中引入交叉验证以获得更稳定的模型，并以AUC 的值作为模型优化测度，采用差异进化算法优化SVM 涉及的参数。同时，结合实际临床要求，通过优化后模型的性能指标曲线构建阈值查找表，选择阈值进行测试验证及PLC 临床预警。

1 基本原理

1.1 支持向量机

SVM[18-19]具有良好的泛化和分类能力，在解决模式识别的问题上成效显著，已广泛应用于目标检测[20]，医疗诊断[21]以及工程预测[22]等领域。它的最终目标是寻找一个分类超平面，使得两类样本的分类间隔最大。如图1 所示，圆圈和方块分别代表一类样本，经过训练后得到最优分类超平面H。

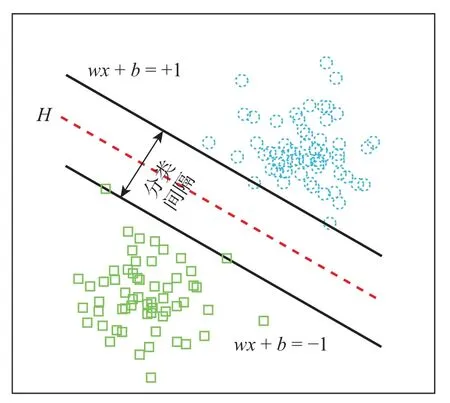
图1 支持向量机原理Figure 1 Principle of support vector machine

假设给定一个特征空间上的训练数据集，T={(x1,y1),(x2,y2),··· ,(xi,yi)}，xi ∈Rn为第i个特征向量，yi ∈{+1,−1}(i=1,2,··· ,k) 为xi的类别标签，(xi,yi) 为样本点。算法的关键是建立具有最大分类间隔的超平面，相当于求解式(1)，即

式中：ω为超平面的法向量，b为超平面的常数项，xi为训练样本，yi为样本点类别，C为惩罚系数，ξi为误差项。

然而，在实际应用中经常会遇到线性不可分的样例。为了解决维度爆炸的问题，引入核函数，先在低维空间计算，再将分类效果显示在高维空间。转化为求式(2) 的最优问题，即

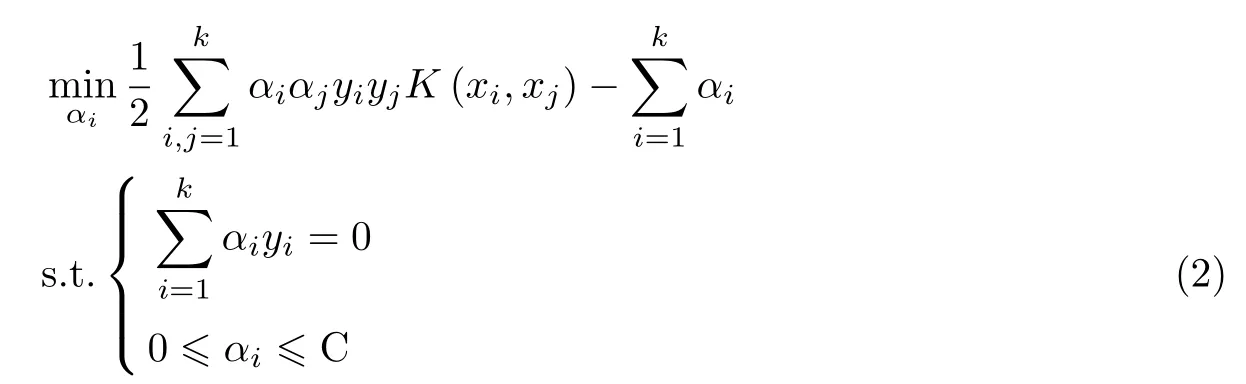
核函数的选择往往需要依据相关领域的先验知识，常用的核函数有线性核函数、多项式核函数、Sigmoid 函数和径向基函数（radial basis function, RBF）[13]。本文中使用的核函数为RBF：

1.2 差异进化算法

惩罚系数C和核函数参数σ不仅决定了SVM 分类结果的准确性，同时还影响预测精度和泛化能力。本文采用差异进化（differential evolution, DE）算法[23-25]对上述参数进行优化。DE 算法广泛用于解决一些非线性、非凸、多峰和不可微分等实数参数问题，已成为最具竞争力和最全面的进化计算算法之一，并在不同科学技术领域成功解决了众多实参数世界的问题[26-27]。

DE 算法需要3 个主要控制参数：变异因子F，交叉概率Cr和种群规模NP。优化过程包括初始化、变异、交叉以及选择操作，对初始种群进行相应操作得到新一代种群，在原个体和新个体之间进行选择，从而将适应度高的个体保存到下一代。差异进化算法的参数优化流程如图2 所示。

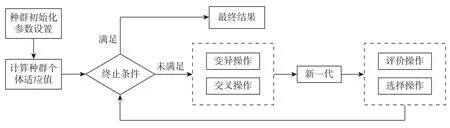
图2 差异进化算法流程Figure 2 Process of differential evolution algorithm

差异进化算法主要包括以下几个步骤：

步骤1初始化随机产生种群N，计算公式为

式中：N,Nmin,Nmax∈RD×Np；Nmin和Nmax分别是个体的最小和最大值；D为需要优化的参数个数。

步骤2依次对个体进行适应度值评估f(Nc)，其中，Nc指当前个体，c为个体序号，c=1,2,··· ,Np。然后选择适应度值最高的个体作为当前结果。

步骤3利用变异和交叉操作改变种群个体以形成新个体，计算公式分别为

式中：Vc,G为变异后个体；G表示当前代数；r1,r2,r3为随机生成的个体序号，它们不等于当前个体序号。再根据交叉因子确定新个体变量来自变异后个体或原始个体，i为个体中变量的序号，ui,c,G,vi,c,G,ni,c,G分别为交叉后、变异后以及原始个体中的变量。

交叉操作之后判断个体是否超出规定范围，如果超出范围，则对其重新赋值，计算公式为

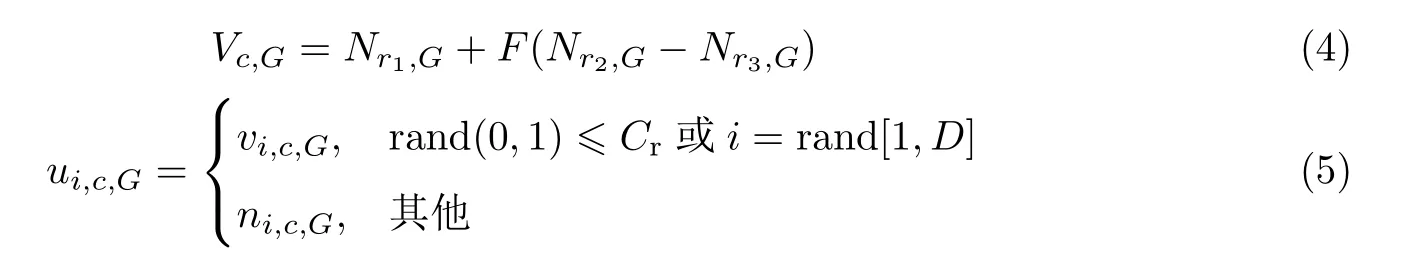
步骤4对新一代种群个体进行评估选择，如果经过交叉操作后的个体适应度值优于原有个体，则原有个体将被替换，计算公式为

式中：Uc,G为交叉操作之后的个体。并且，如果该个体优于最佳个体，则替换最佳个体。

步骤5重复步骤3 和4，直至满足终止条件。

本文将AUC 作为评价个体适应度的准则，其取值越高则说明该个体的适应度越强。AUC的取值范围一般在0.50 和1.00 之间，范围属于[0.50, 0.70] 时表示预测准确性较低，属于[0.70, 0.90] 时表示预测准确性中等，属于[0.90, 1.00] 时表示预测准确性较高。

1.3 交叉验证

引入交叉验证（cross validation, CV）用来验证SVM 性能，其基本思想是将数据集分成训练集和验证集两部分。利用训练集建立模型，验证集验证模型分类性能，最终得到错误率最低的模型。本文使用k-折交叉验证（k-fold cross-validation），相对于留一法，该交叉验证具有计算精度高且计算量小的优点。

2 差异进化算法改进的支持向量机模型

PLC 早期筛查实验流程如图3 所示，首先在保证数据有效性以及通用性的基础上对临床检验数据集进行预处理，然后将其拆分为训练和测试数据集，通过改进的SVM 方法训练得到分类模型，再结合临床需求获取其性能指标曲线以及阈值查找表得到分类阈值，最后利用阈值对测试数据进行预测。其中，在改进的SVM 方法以RBF 作为核函数，以AUC 作为参数优化测度，以惩罚系数和核函数参数为DE 的优化对象，另外加入交叉验证防止模型出现过拟合，最后利用混淆矩阵、Kappa 系数等性能评价指标对分类模型进行评估。

图3 原发性肝癌早期筛查法流程Figure 3 Process of PLC early screening method

2.1 数据集

2.1.1 数据集来源

本文实验采用东方肝胆外科医院检验科的数据，共收集样本1 069 例。样本数据主要包括个人基本信息、血液常规、尿液常规、粪便常规、肝功能生化标志物、肿瘤标志物、肾功能生化标志物、糖脂代谢、特定蛋白、感染标志物等大类。特征数量为78～140 不等，数据分为健康、良性病变和恶性肿瘤（原发性肝癌）3 类。

2.1.2 数据集预处理

为保证分类方法训练以及预测的准确性、可靠性以及通用性，将去除数据集中明显不完整的特征以及健康人群中较少检测的肿瘤标志物所对应的特征列，并且将数据集中不能识别的字段进行相应处理，使数据符合算法要求。最终用于建模和测试实验的临床常规检验指标数据集共包含1 047 例样本和30 个特征数量。

2.1.3 数据集分组

把经过上述预处理后的1 047 例样本分为训练数据和测试数据，随机选取600 例为训练数据集，其余447 例为测试数据集，数据在不同数据集的分布情况如表1 所示。

表1 训练与预测数据量Table 1 Number of training and prediction data 例

2.2 性能评估指标

本文利用混淆矩阵得到以下性能评估指标：敏感度（SE），特异度（SP），约登指数（Youden index, YI），准确度（ACC），ROC 曲线，AUC 以及Kappa 系数。

2.2.1 混淆矩阵

二分类问题的混淆矩阵如表2 所示，阴性表示健康，阳性表示患病。其中：TN 表示正确预测出健康人群，FN 表示患者被错误预测为健康人群，FP 表示健康人群被错误预测为患者；TP 表示正确预测出患者。

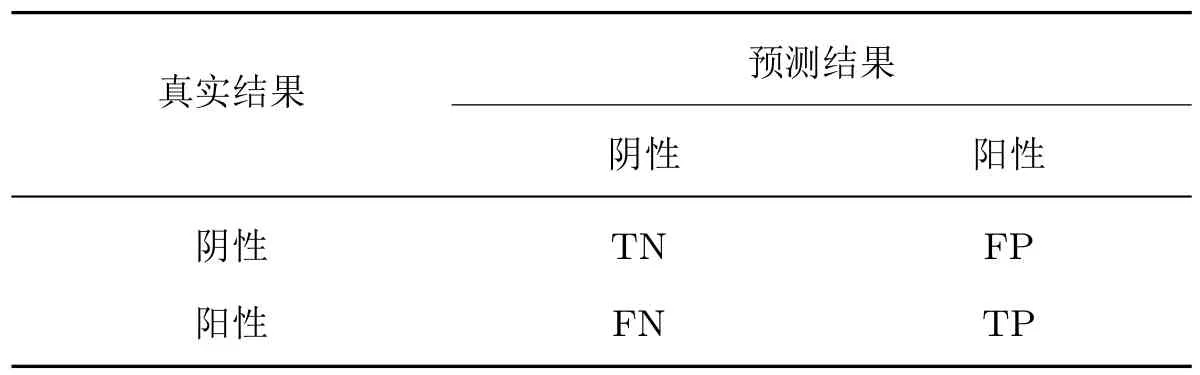
表2 二分类问题混淆矩阵Table 2 Confusion matrix of 2-class

基于混淆矩阵进一步求出性能评估指标SE，SP，YI 和ACC 的值，具体公式为：

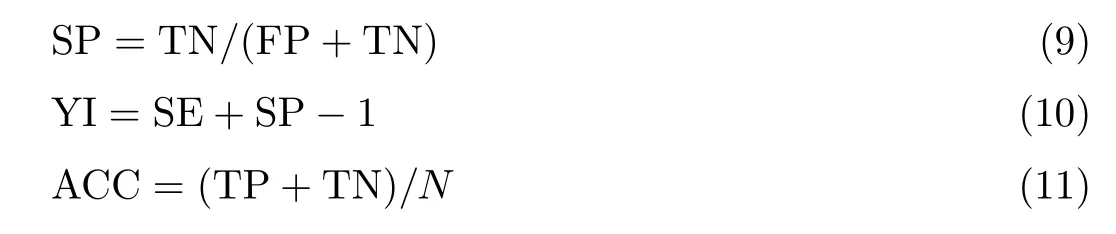
式中：N为样本总数。

2.2.2 ROC 曲线和AUC

ROC 曲线综合反映了敏感度和特异度的相互关系。如图4 所示，横坐标为假阴性率（false positive rate，FPR），纵坐标为真阳性率（true positive rate, TPR），曲线上的点表示在当前分类阈值下对应的SE 和（1-SP）的值。即使在两类样本的分布产生变化或样本分布不平衡时，ROC 曲线也基本保持原貌。AUC 即为ROC 曲线下方与坐标轴所围成封闭图形的面积，它是综合评价判别算法优劣的二维直观描述。

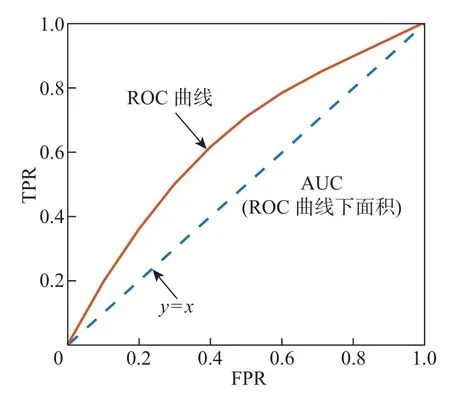
图4 ROC 曲线与AUCFigure 4 ROC curve and AUC

2.2.3 Kappa 系数

上述评价方法只能用于评估二分类问题性能，故引入Kappa 系数来衡量三分类情况，计算方式基于表3，如式(12)～(14) 所示。它的取值范围在−1.00～1.00 之间，通常落在0～1.00 之间，当值为−1.00 时说明结果与实际完全不一致。Kappa系数与一致性级别如表4所示。

表3 三分类问题混淆矩阵Table 3 Confusion matrix of 3-class

表4 Kappa 系数与一致性级别Table 4 Kappa index and consistency level

2.3 实验模型

实验所建立的两层模型可用于实现三分类，实现步骤如下：第1 层区分健康样本与患病样本；第2 层区分患病样本属于良性病变还是恶性肿瘤；最后将两层结果组合得到三分类的预测结果。

两层模型的建立均基于SVM，利用了DE 来优化惩罚系数C和核函数参数σ，并用AUC评价优化效果。在参数优化时，C和σ分别表示成指数形式2m和2n，其中m和n为一个2维的个体，种群规模Np取100，变异因子F取0.5，交叉概率Cr取0.9，进化终止条件是适应度评价次数不大于10 000 次。在进化过程中始终将m和n限制在[−8,8] 范围内，变异策略选择DE/rand/bin/1[23]。为防止过拟合，训练过程采用5 折交叉验证模式[28]，先利用网格法对参数值的取值范围进行粗筛以确定参数的范围，再使用差异进化算法优化参数。

3 实验结果与分析

传统的机器学习算法相对于深度学习方法更适用于小样本数据，且可在短时间内尝试多种算法，从而方便改进模型。实验分别使用逻辑回归（logistic regression, LR）、决策树（decision tree, DT）、随机森林（random forest, RF）、梯度提升决策树（gradient boosting decision tree, GBDT）以及SVM 建立模型并进行预测。其中的对比实验采用随机搜索的寻参方式。

各模型的ROC 曲线分别如图5 和6 所示，可以看出：无论是在建模还是在预测过程中，使用SVM 方法的AUC 值不低于其他几种算法，表明该方法建模效果更好，且使用DE 算法改进参数选取方式后模型的性能得到进一步的提高。用以上模型对测试数据进行预测，其结果如表5 和6 所示。可以看出：未使用DE 算法优化SVM 所构建的模型，其特异度值处于各

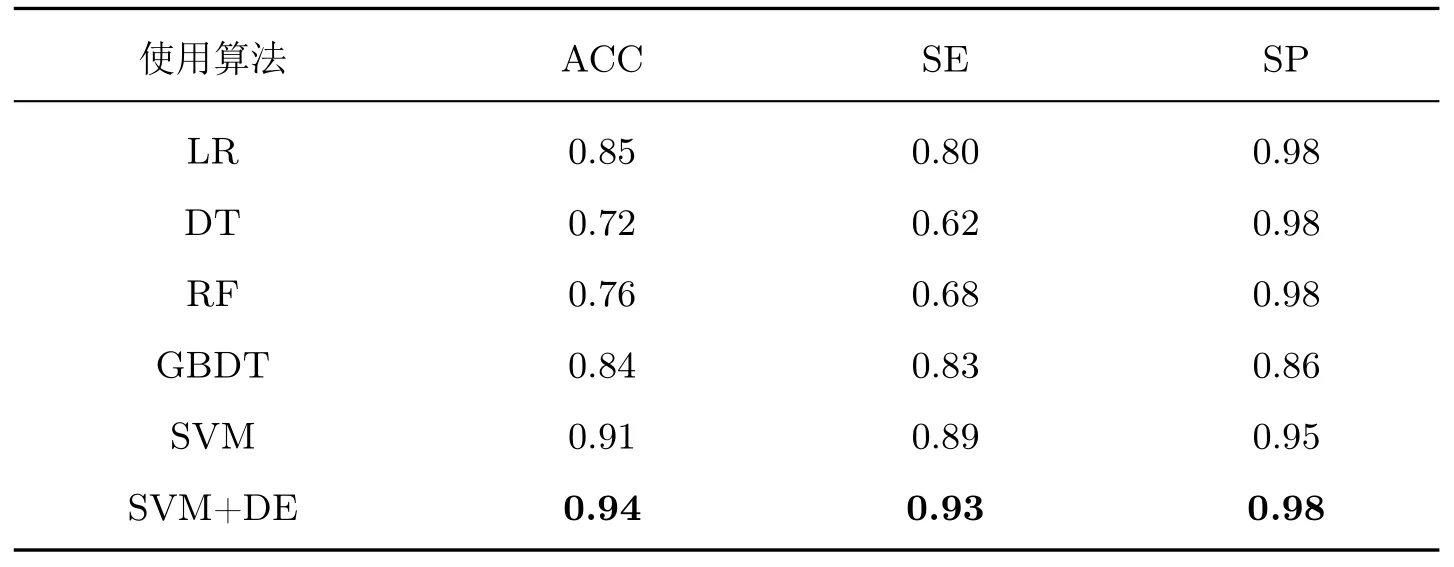
表5 第1 层分类结果对比Table 5 Classification results of the first hierarchical layer

图5 第1 层模型ROC 曲线Figure 5 ROC curves of the first hierarchical layer model

3.1 方法对比

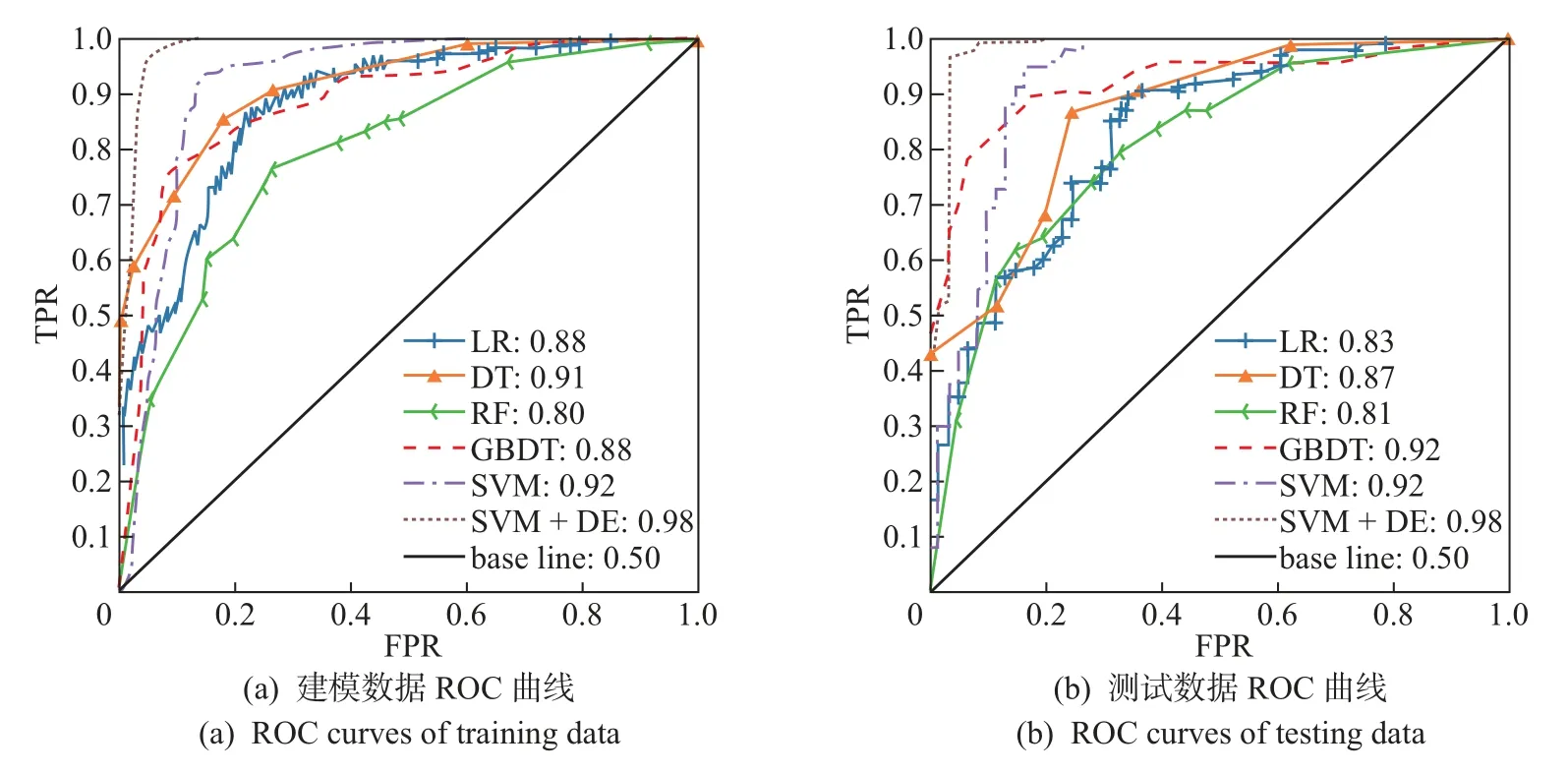
图6 第2 层模型ROC 曲线Figure 6 ROC curves of the second hierarchical layer model

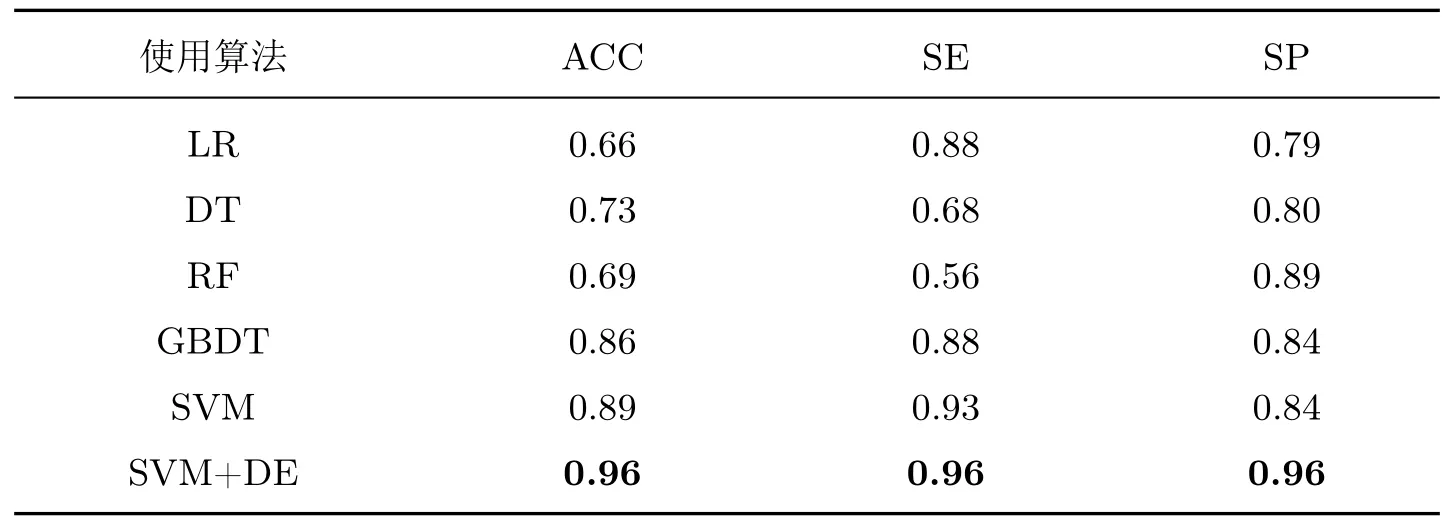
表6 第2 层分类结果对比Table 6 Classification results of the second hierarchical layer

种算法的中等位置，准确度以及敏感度处于领先位置；而优化SVM 后，模型的3 个指标值均为最高，显然优化后的模型具有一定的优越性。

3.2 结果与分析

3.2.1 分层结果

在实际临床中常有提高敏感度和降低误诊率的需求，因此需要辅助医生根据要求选择合适的分类阈值。基于训练模型画出2 次二分类对应的性能指标曲线，如图7 所示，横轴代表阈值，纵轴表示性能指标对应的值，指标包括ACC、SE、SP 以及约登指数。以第1 层建模约登指数不小于0.98 且第2 层不小于0.92 为例，得到两层的阈值范围分别是[−0.74,0.98] 和[−0.74,0.54]。对上述范围10 等分得到如表7 和8 的阈值查找表。

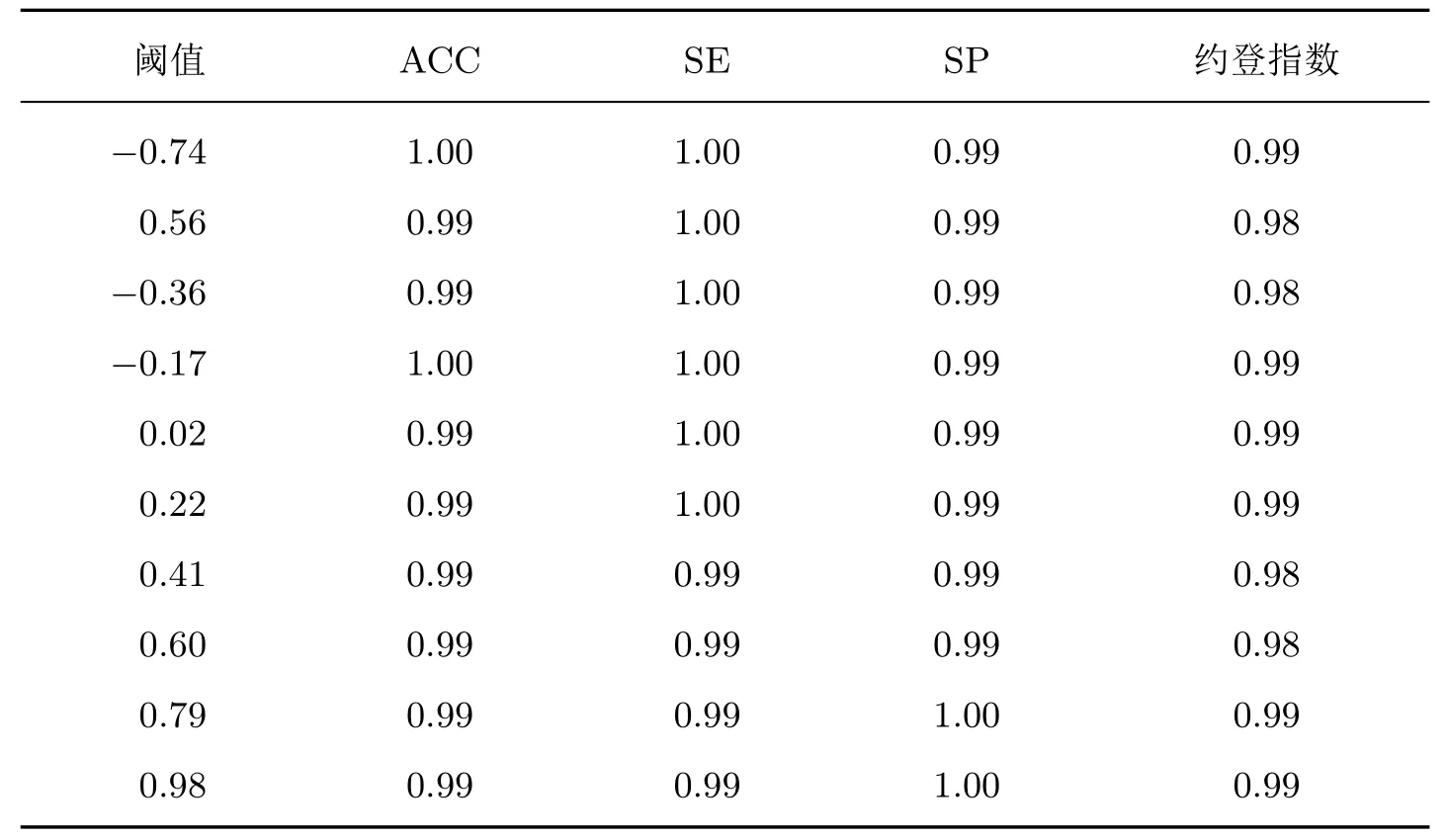
表7 第1 层分类阈值查找表Table 7 Cut-offlookup table of the first hierarchical layer

图7 模型性能指标曲线Figure 7 Index curves of the model performance

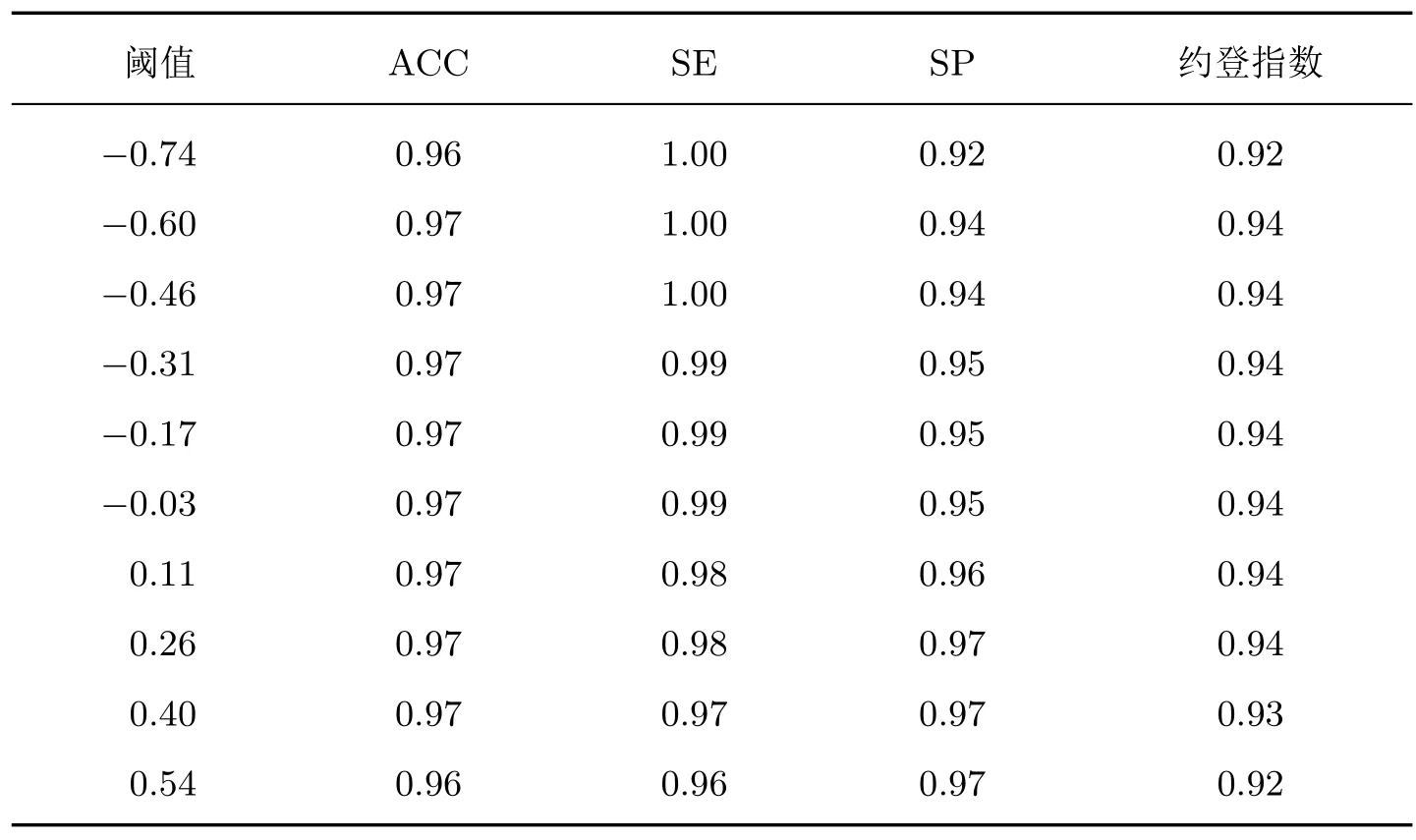
表8 第2 层分类阈值查找表Table 8 Cut-offlookup table of the second hierarchical layer

3.2.2 整体结果

选取两层分类阈值查找表中SE、ACC、SP 最高的阈值为例，将其按层次两两组合，得到三分类结果如表9 所示。可以看出，该方法在预测集的表现随着选取阈值的标准不同会产生相应的变化，同时大部分Kappa 系数依然能够保持在几乎一致水平，说明该方法具有优秀的分类性能。而且根据性能指标的要求选取两层的阈值组合后进行预测，有助于临床筛选，并在满足实际应用需求的同时保证预测的准确性和灵活性，最优情况时Kappa 系数可达到0.90，ACC 可达到0.94。因此，本文提出方法可用于肝癌早期筛查和早期预测。

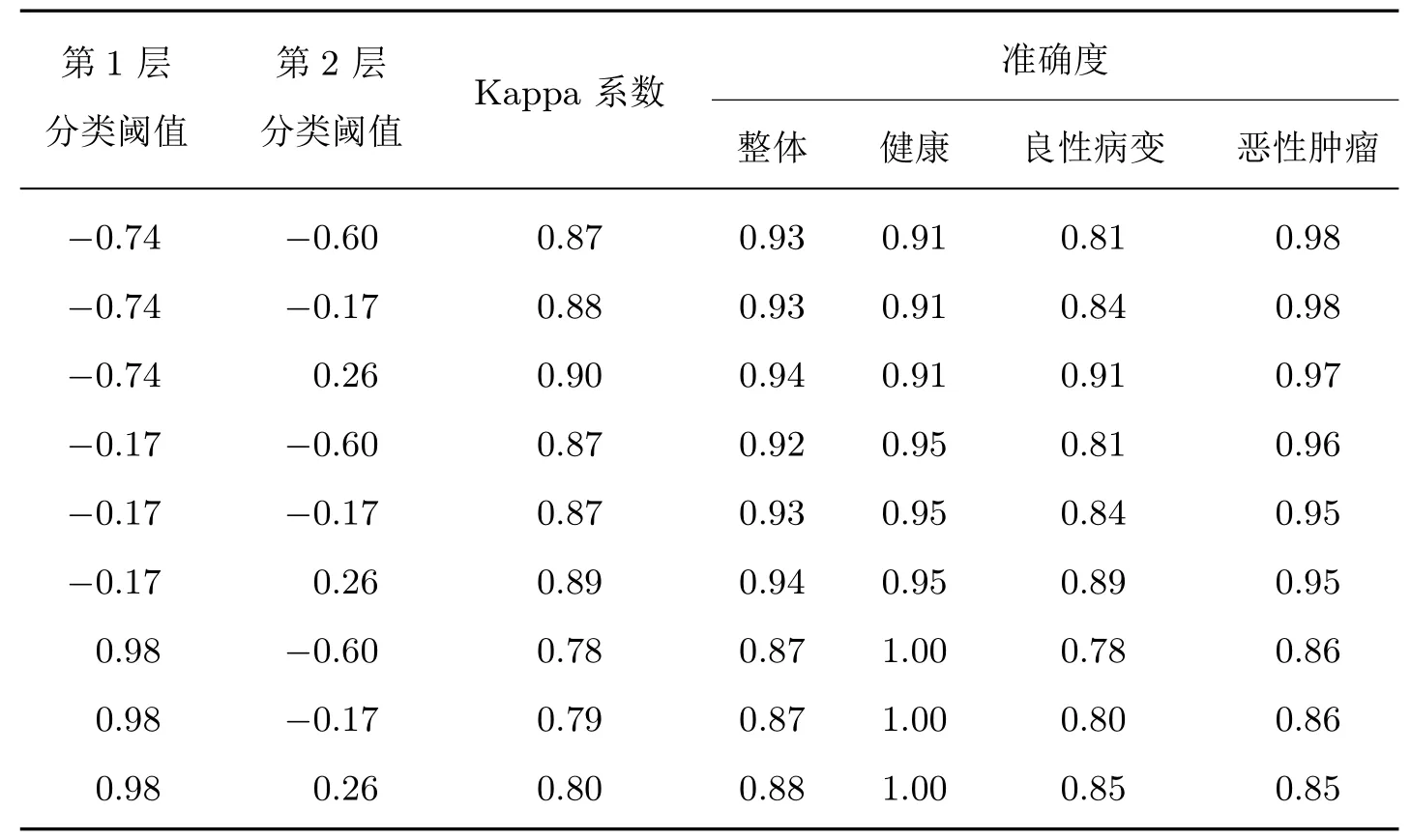
表9 三分类预测结果Table 9 Predicted results of 3-classification model

4 结 语

PLC 的早期预测和预防是提高患者生存率最有效的途径。虽然甲胎蛋白等肿瘤标志物被广泛应用于肝癌诊断，但其敏感性和特异性等指标并不理想，假阴性率高。本文基于DE 改进后的SVM 模型提出了自定义阈值的层次分类方法，最终实现三分类。并且实验利用临床检验中肿瘤标志物之外的常规数据指标，根据临床对评价指标的不同要求定义分类阈值，使模型在保证可靠性的同时具有了灵活性。因为数据样本有限，所以本文通过对比几种传统的机器学习算法后，采用在小样本上具有优越性能的SVM 方法进行研究。随着实验数据的积累，后期会考虑使用深度学习相关技术进行建模、预测与分析。

(编辑：管玉娟)