基于CAE的车架结构模态分析及优化设计

姚明镜，唐 璇，贾曾浩

(1.成都理工大学工程技术学院，四川 乐山 614000) (2.核工业西南物理研究院，四川 成都 610225)

随着汽车工业的发展和人们对于安全越发重视，消费者对车辆各方面的性能提出了更严格的要求。与此同时，由于对汽车轻量化的要求越来越迫切，因此通过强化汽车车架结构，以此保证驾驶员的人身安全就显得非常重要[1]。车架是汽车的关键承载部件，其强度直接影响着驾驶室乃至整车的使用性能。实践中，运用CAE可以有效地计算车架在各种工况下的响应[2]，从而为相关的优化设计、制造提供理论依据，可以在很大程度上提高车辆驾驶的安全性和舒适性。

1 结构力学理论基础

本文利用有限元软件对某汽车侧围零件进行优化及模拟计算，结合分析模态得出零件的振动特性，再根据实际经验具体优化零件的物理属性，并提出合适的零件特征结构优化手段，以改善零件的一阶模态频率，间接提高车身的动态性能[3]。其流程如图1所示。

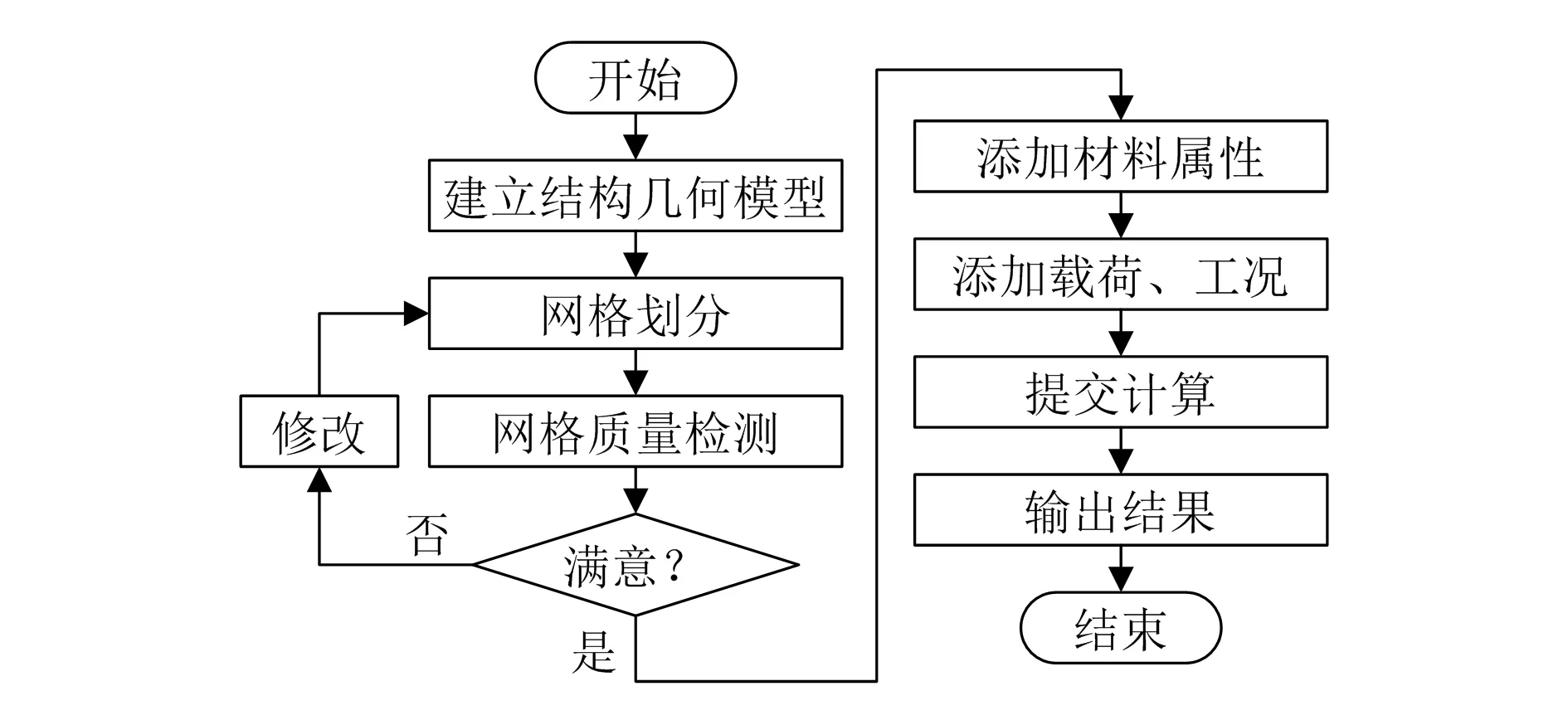
图1 有限元分析流程框图

在实际中，汽车零件的钣金材料通常认为是材质均匀，无明显缺陷，结构的物理性能(如质量和弹性)不是分散单独的，从而引出了很多无法计数的自由度。分析的时候通常是把目标的自由度分散为有限个。由振动理论可得，在已知范围内坐标系中的振动是由有限个单独振动共同组成，每个部件的振动都有它特定的振动特性，而这个整体的振动就是目标的固有频率，振动的方式也就是模态振型[4]。

本文利用振动理论计算模态，建立相关的微分方程组使方程组解耦，形成一组以模态坐标及模态参数描述的独立方程，以便求出系统的模态参数[5]。根据振动分析理论，得出连续体离散后的振动微分方程：

MX(t)1+CX(t)2+KX(t)=F(t)

(1)

式中：M，C，K分别为离散结构体系的质量矩阵、阻尼矩阵及刚度矩阵；X(t)，F(t)分别为各点的位移响应矩阵和激励力向量；X(t)1，X(t)2为X(t)的一、二阶导数。X(t)1，X(t)2，X(t)是用振动系统的物理坐标系表示的。

2 结构分析及优化设计

本文根据车辆驾驶室结构形式和可能受力特点建立有限元模型。

2.1 模型建立及参数设置

该零件的所有网格都应满足如表1所示的质量要求。图2所示的侧围网格模型共有60 240个节点、58 478个结构单元(内含57 352个四边形单元、1 126个三角形单元，其中三角形单元占网格总数的1.9%)。三角形单元因为刚度很高，不易变形，所以不宜过多选用。目前主要还是采用四边形单元网格，三角形网格数量需控制在5%之内。检测网格质量时，还应检查其网格的连续性，确保模型中的网格相连续，如图3所示。本文中网格质量参数的确定依据工程实际及文献[6]中的网格质量判定指标确定，见表1。

表1 网格质量

图2 侧围网格模型

图3 网格连续性检查

零件模态分析的具体步骤如下[7-8]：

1)建立零件模型并进行网格划分；

2)利用Nastran进行有限元模型计算；

3)对模型的一阶扭曲模态和弯曲模态进行数据记录和分析；

4)根据模态分析结果，对模型结构进行优化设计。

对建好的模型进行0～100 Hz的频率激励，分析弹性模态，所得结果见表2。

表2 关键模态

通过计算得到了侧围0～100 Hz的模态参数，由于该模型是简化结构，因此出现了预期的一阶扭曲模态(图4)和弯曲模态(图5)。本次计算中，零件最小固有频率为19.71 Hz，此频率偏低，容易受发动机怠速及运输工况影响产生共振，增大车身振动，对侧围零件造成损害。

图4 扭曲模态

图5 弯曲模态

车辆在运行的时候，会受到多种激励，最主要的是发动机的激励，因为此振动源会一直伴随车辆的运行。若汽车侧围出现共振，将会极大地影响车辆乘坐的舒适性。发动机振动频率与输出转速有关，其关系如下：

(2)

式中：f为激励频率，Hz；n为发动机转速，r/min；m为发动机缸数；δ为发动机转速上下浮动误差，r/min。

假设某四缸柴油发动机的怠速为600 r/min，转速上下浮动50 r/min，将数据代入式(2)可得发动机激励频率为18.33～21.67 Hz，而侧围一阶扭曲模态频率刚好在此频段里，很容易引发侧围的共振。

因为通过改变发动机的转速来解决此可能出现的问题成本过高，所以提高侧围弯曲模态的固有频率就成为非常可靠的办法。

2.2 侧围模态结构优化

对侧围进行优化，主要有两种方式，其一可以通过改变材料、形状和结构实现整体改变，但侧围零件在车身表面，任何的改动都会影响车辆的外观；侧围板件的材料也应和车身其他部位材料大致相同，从而为批量生产节约成本；增加侧围总体厚度不仅会对车辆自重产生较大的影响，还会对其他零部件性能产生间接影响。由此可知，采用整体改变的方式是不可取的。其二根据工程实际经验可知两横梁是连接两边大框架的唯一部分(如图6所示)，此目标的性能会大大影响侧围总体的固有模态，因此可通过改变侧围局部横梁结构的材料属性和厚度或增加特征筋来实现优化[9-10]。

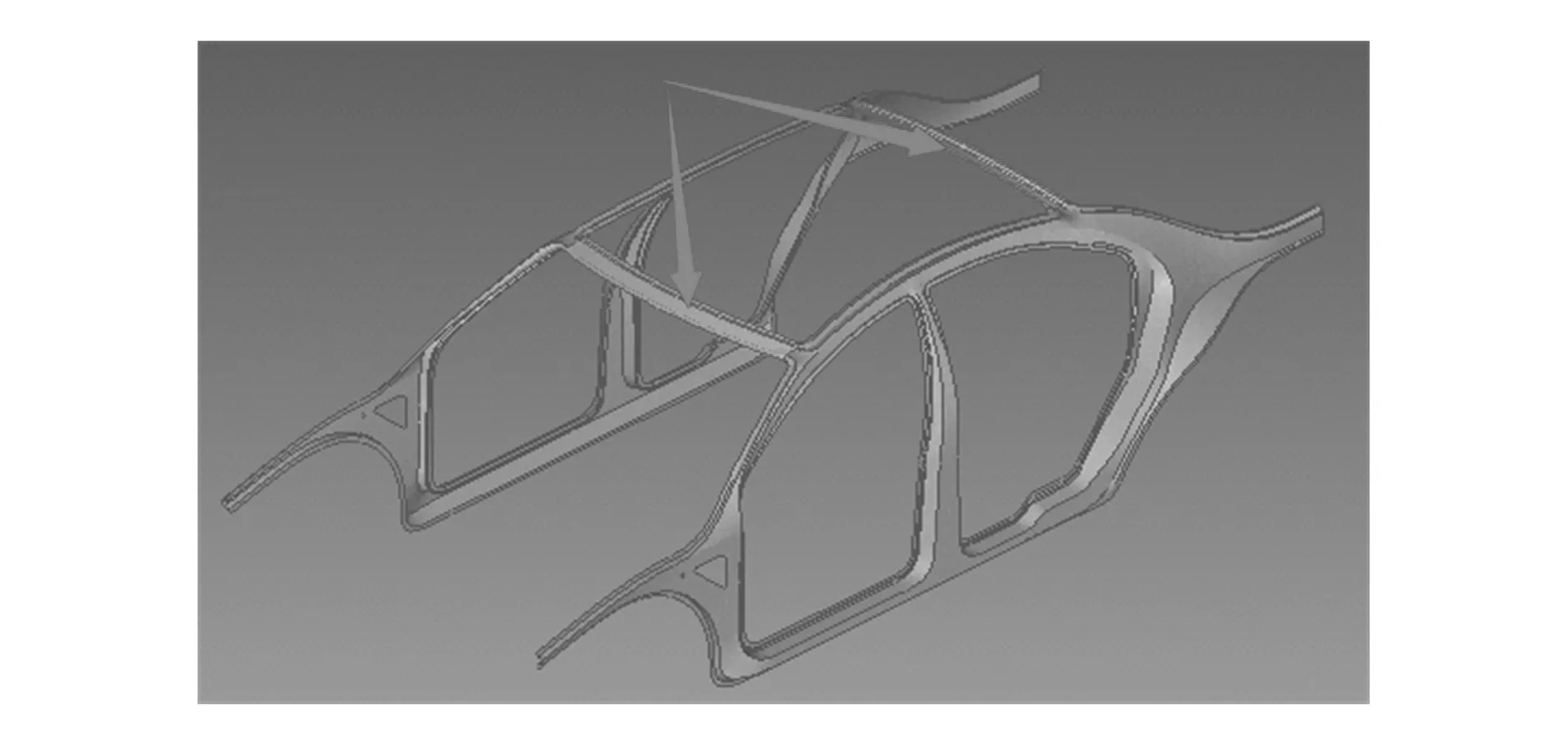
图6 侧围的两横梁

2.2.1改变横梁厚度

优化时，板厚的变化会有多重效果，要达到最终理想效果，需要建立出优化目标与板厚变化的相关函数关系，找出在约束范围内的板厚最佳效果——提高一阶扭曲模态的频率。

通过分析，该优化模型可以表示为:

设计变量：

x=[x1,x2,…,xi,…,xn]

(3)

目标函数：

w1(x)⟹max

(4)

满足约束条件：

(5)

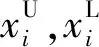
通过优化目标与板厚变化的相关函数关系分析并把结果图像化，得到图7。

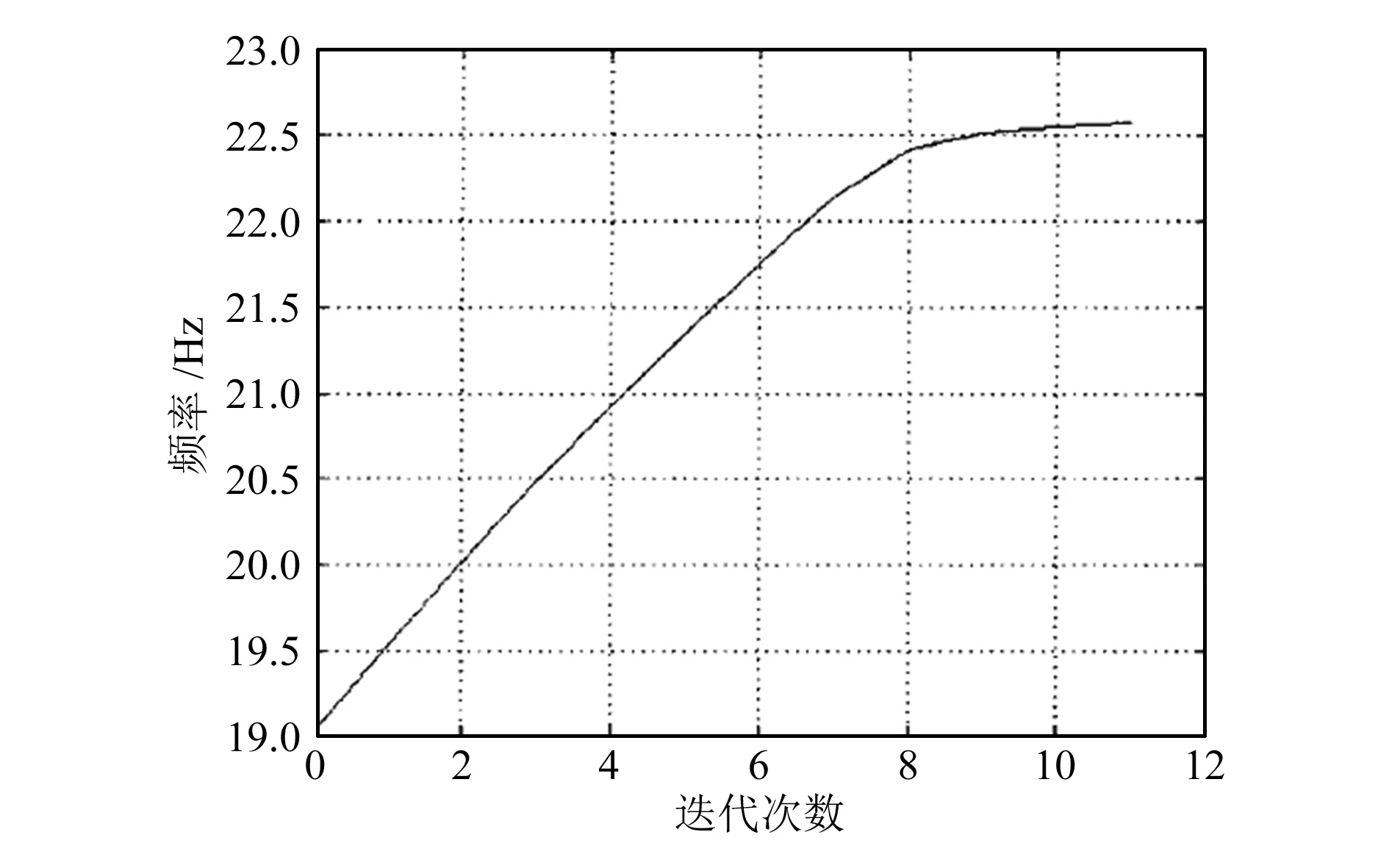
图7 扭曲模态和侧围质量迭代变化的关系图

由图可得，随着迭代次数的增加，扭曲模态上升，从第8次开始，模态频率的变化逐渐平缓，因此取累加8次为最优方案，即横梁板厚增加为2.0 mm。厚度优化后的车架结构模态如图8和图9所示，优化前后重要模态的对比见表3。

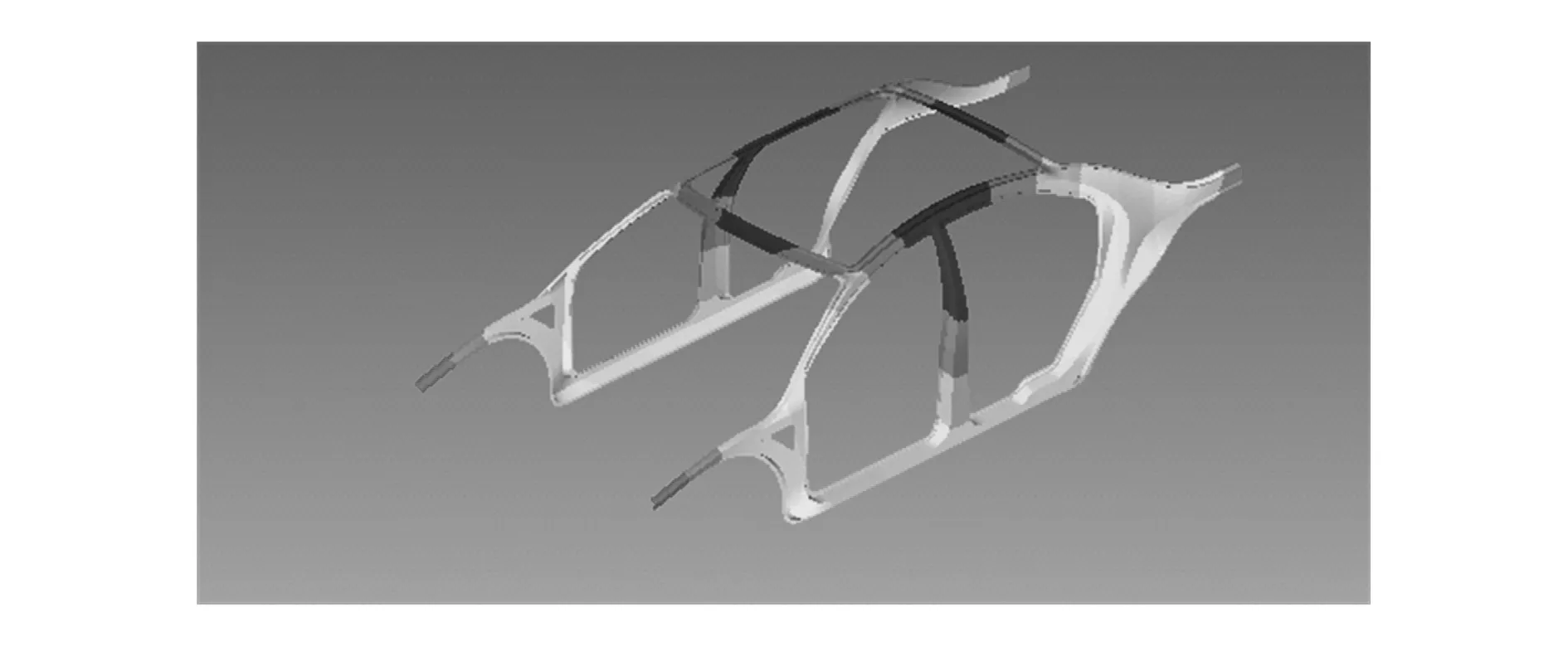
图8 改变厚度优化后扭曲模态

图9 改变厚度优化后弯曲模态

表3 厚度优化的模态变化单位：Hz

由计算结果可知，随着车身横梁板厚增大，扭曲模态频率升高3.46 Hz，弯曲模态频率升高2.61 Hz。优化后，侧围扭曲模态频率增加为23.17 Hz，扭曲模态频率不在发动机的激励频率范围内，不会产生共振。

2.2.2改变横梁材料

考虑到横梁在整个车架中的受力情况，横梁材料以钢为主，原始方案采用的是Q235，优化后材料变为45钢，材料优化后的车架结构模态如图10和图11所示，优化结果见表4。

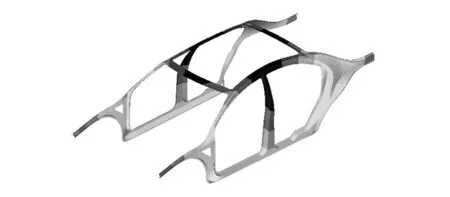
图10 改变材料优化后扭曲模态

图11 改变材料优化后弯曲模态

表4 材料优化的模态变化单位：Hz

由计算结果可知，改变横梁材料，所有阶段的模态变化很小，因此改变横梁材料的优化方式不可取。

2.2.3前横梁加特征筋

结合工程实际对该车架采取前横梁加特征筋的方式进行优化，加特征筋优化后的车架结构模态如图12和图13所示，结果见表5。

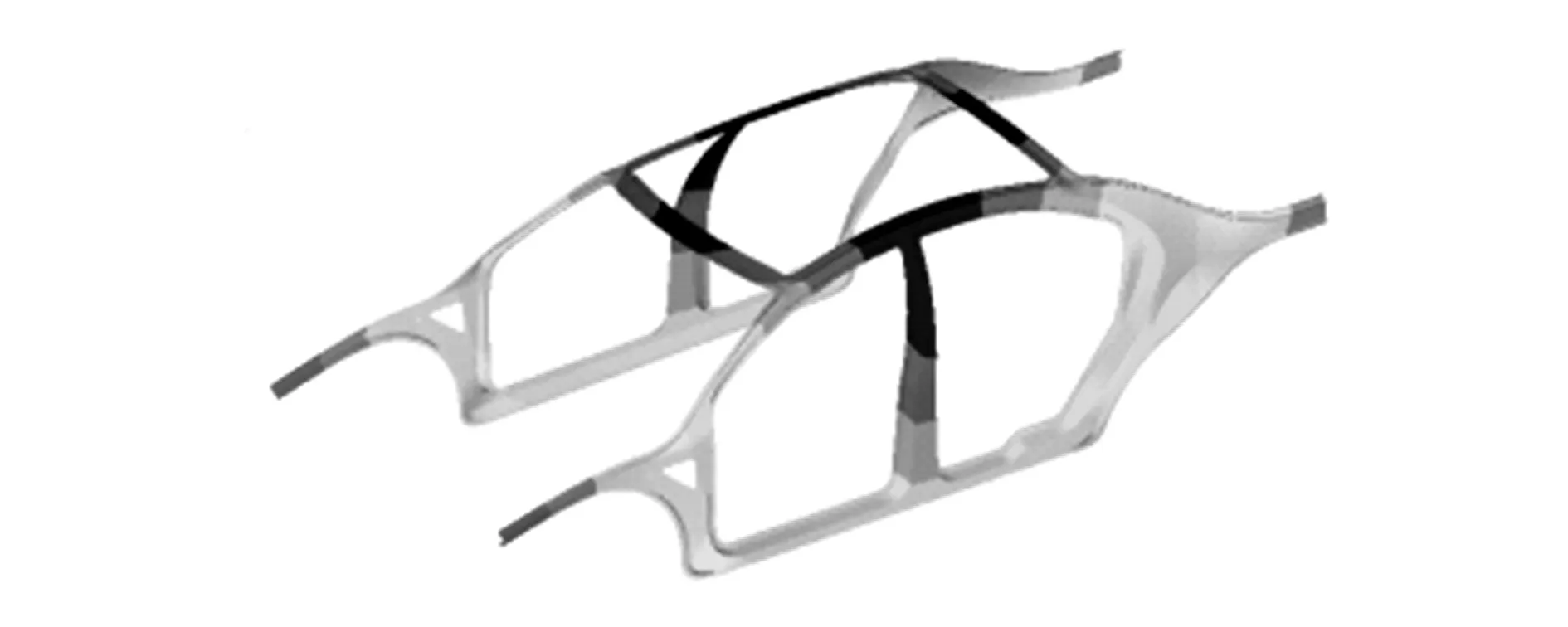
图12 前横梁加特征筋优化后扭曲模态

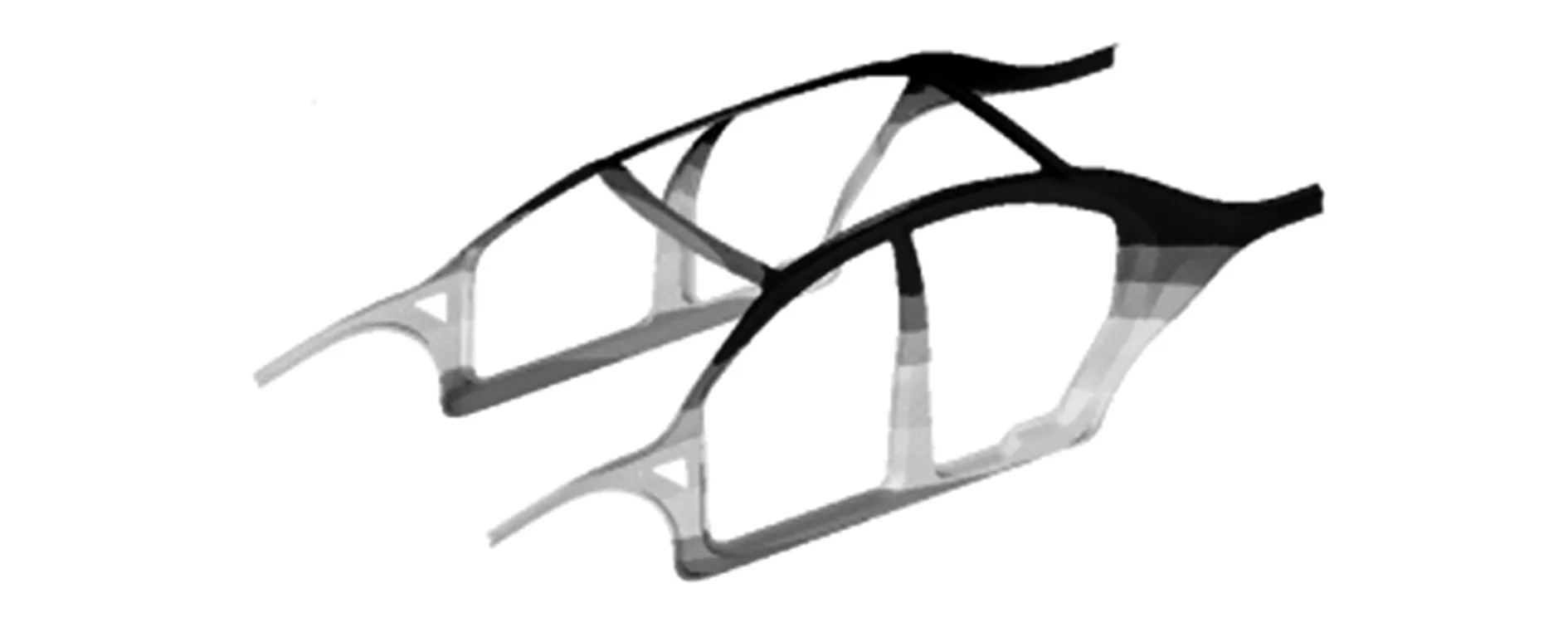
图13 前横梁加特征筋优化后弯曲模态

表5 加特征筋的模态变化单位：Hz

由计算结果可知，前横梁加特征筋，所有阶段的模态都发生了变化，扭曲模态增加了0.40 Hz，弯曲模态增加了0.75 Hz。扭曲模态处于共振范围，此方案不可取。

3 结束语

本文利用有限元软件对汽车车架进行结构分析，通过增大车架结构横梁厚度、更换材料、增加特征筋3种方式进行结构优化，综合各优化结果可知，增大车架结构横梁厚度的方式可以使弯曲模态和扭曲模态的频率处于发动机怠速频率范围外，不会产生共振，从而有效提高了车辆的安全性和舒适性。本文的研究成果可以为汽车工艺优化和改进提供一定的参考。