漂浮基空间机械臂鲁棒自适应滑模神经网络控制
徐桂新,宋 齐,于潇雁,陈 力
(1.福州大学机械工程及自动化学院,福建 福州 350116)
(2.流体动力与电液智能控制福建省高校重点实验室(福州大学),福建 福州 350116)
航天器处在具有高辐射、高温差、微重力等特点的环境中,为了实现其运行过程中的维修、加注、回收等操作,空间机器人得到了越来越广泛的应用。与地面固定机器人系统相比,空间机器人具有动力学系统强耦合、非线性控制等特性,需要解决的问题较为复杂,因此对其相关的研究引起了国内外科学研究人员的广泛重视[1-2]。许多国家的科学家们设计出多种机械臂控制方法,如PID(proportion,integral,differential)控制[3]、自适应和神经网络结合控制[4-5]、模糊自适应控制[6]、滑模控制[7]、鲁棒控制[8]、奇异摄动法控制[9]、自适应反演控制[10]等方法。Liu等[11]设计了一种限定时间的自适应神经网络反馈控制方法,该方法解决了机械臂不确定项的补偿问题,但是却强化了外部扰动对系统的鲁棒性;洪昭斌等[12]设计了一种基于神经网络的空间机械臂控制方法,具有不需要测量、反馈载体位置及移动速度和移动加速度信号等特点;Zhang等[13]设计了一种神经变结构控制器,该控制器具有冗余的控制能力,能避免机械臂末端质量改变对原系统稳定性造成破坏,维持其稳定性;Zhao等[14]研究了基于对称型障碍李雅普诺夫函数(SBLF)与自适应神经网络的跟踪问题,控制器采用了反演和自适应反馈相结合的方法。
但是在受到外界干扰的情况下,以往的研究其空间机械臂的实际轨迹与期望运动轨迹有较大的误差,难以满足实际应用中对于机械臂精确控制的需要。本文提出了一种基于径向基函数神经网络(RBFNNs)的空间机器人鲁棒自适应轨迹跟踪滑模控制方法,该方法结合了滑模控制、自适应技术和不同权值自适应律的RBFNNs机械臂的优点,实现了在外太空环境下的高精度位置跟踪。
1 系统动力学模型
如图1所示,漂浮基空间机械臂系统由漂浮载体、两关节机械臂组成,整个机械臂系统满足动量守恒定律。建立平动的直角坐标系O-XY,各分体沿着平面(X,Y)做平面运动,θ0为本体的姿态角,θi为机械臂第i个关节铰的相对转角(i=1,2),OCi为各分体Bi的质心,ri为OCi的位置矢径(i=0,1,2),rC为系统的总质心C相对于惯性坐标系原点O的矢径,rP为机械臂的末端P点相对O的矢径。
根据系统动能原理并结合拉格朗日第二类方程,得到刚性空间机器人系统载体位置不受控、姿态受控的动力学方程:
(1)
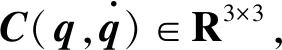
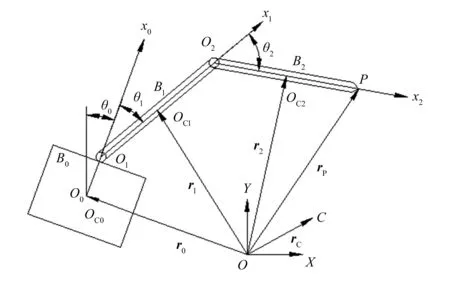
图1 刚性单臂空间机器人系统
假设单臂空间机器人载体姿态角、两个关节铰的转角期望轨迹为qd=[θ0d(t),θ1d(t),θ2d(t)]T,是连续的,则自由漂浮单臂空间机器人系统的动力学方程具有如下性质。
性质1v1‖x‖2≤xTD(q)x≤v2‖x‖2,v1,v2为正常数,∀x∈R3×1。
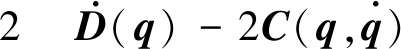

2 基于RBFNNs鲁棒自适应滑模控制的设计
2.1 RBF逼近目标函数
利用RBF(radial basis function)神经网络对模型的不确定因素进行自适应补偿,以提高建模精度。RBF神经网络由三层组成,分别为输入层、隐含层和输出层,如图 2所示。

图2 RBF逼近f(x)
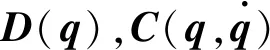
(2)
(3)

实际轨迹与期望轨迹误差e为:
e=qd-q
(4)
(5)
取滑模面s:

(6)
式中:λ=diag(λ1,λ2,λ3),为正定矩阵。综合式(1)、(4)、(5)、(6),得:

(7)
(8)
(9)
2.2 鲁棒自适应滑模控制律设计

(10)
设计如下控制器:
(11)
式中:Ks=diag(Ks1,Ks2,Ks3),为正对角常数矩阵;τs为待设计的鲁棒项。
权值自适应率设置为:
(12)
(13)
式中:FD,FC均为矩阵;KCc,KDd为正常数。
鲁棒项:
(14)
式中:Kp为正常数。为了消除抖振现象,用饱和函数[15]sat(s)代替符号函数sgn(s):
(15)
式中:D为饱和宽度,D、γ均为小的正常数,其中0
(16)
将式(11)代入式(7)得:
(17)
(18)

2.3 稳定性与收敛性分析
(19)
对函数V(t)求导得:
(20)
由性质2,式(20)可写为:
(21)
将式(17)、(18)代入式(21)得:
(22)
(23)
将自适应率式(12)、(13)代入式(23)得:
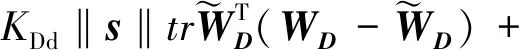
(24)

(25)
将式(14)、(15)代入式(25)得:
(26)
如果|s|>D,则:
(27)
则
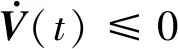
(28)
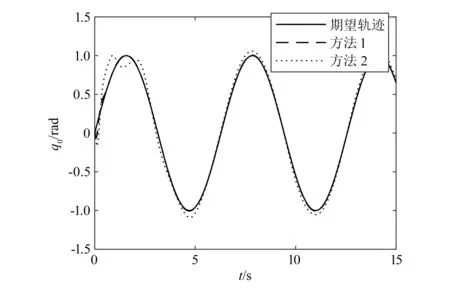
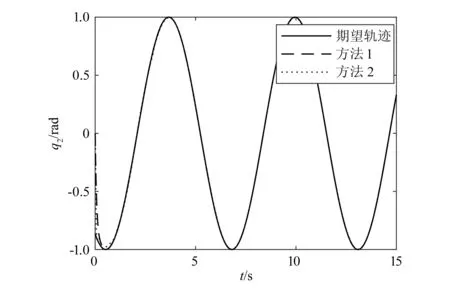
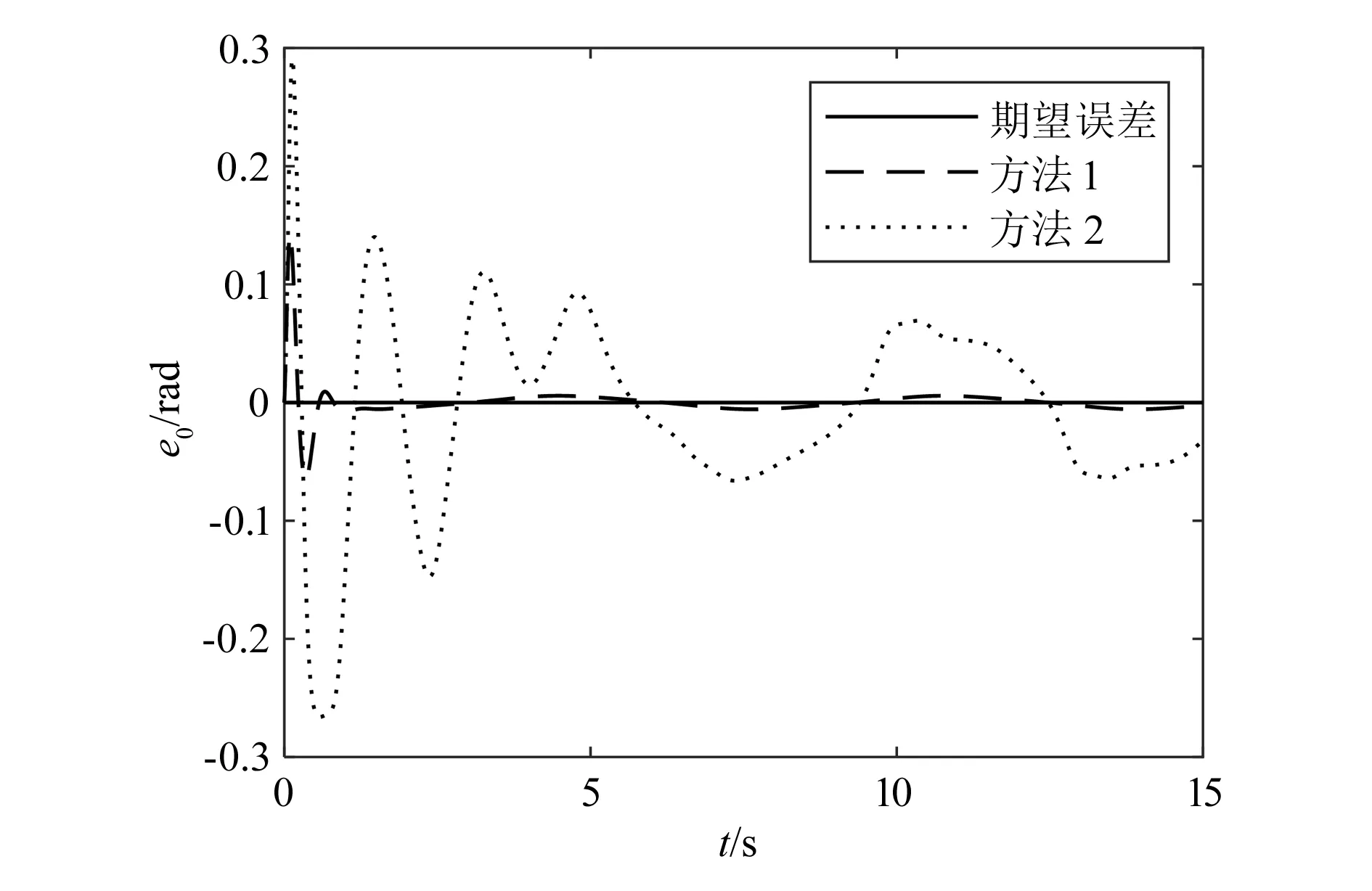
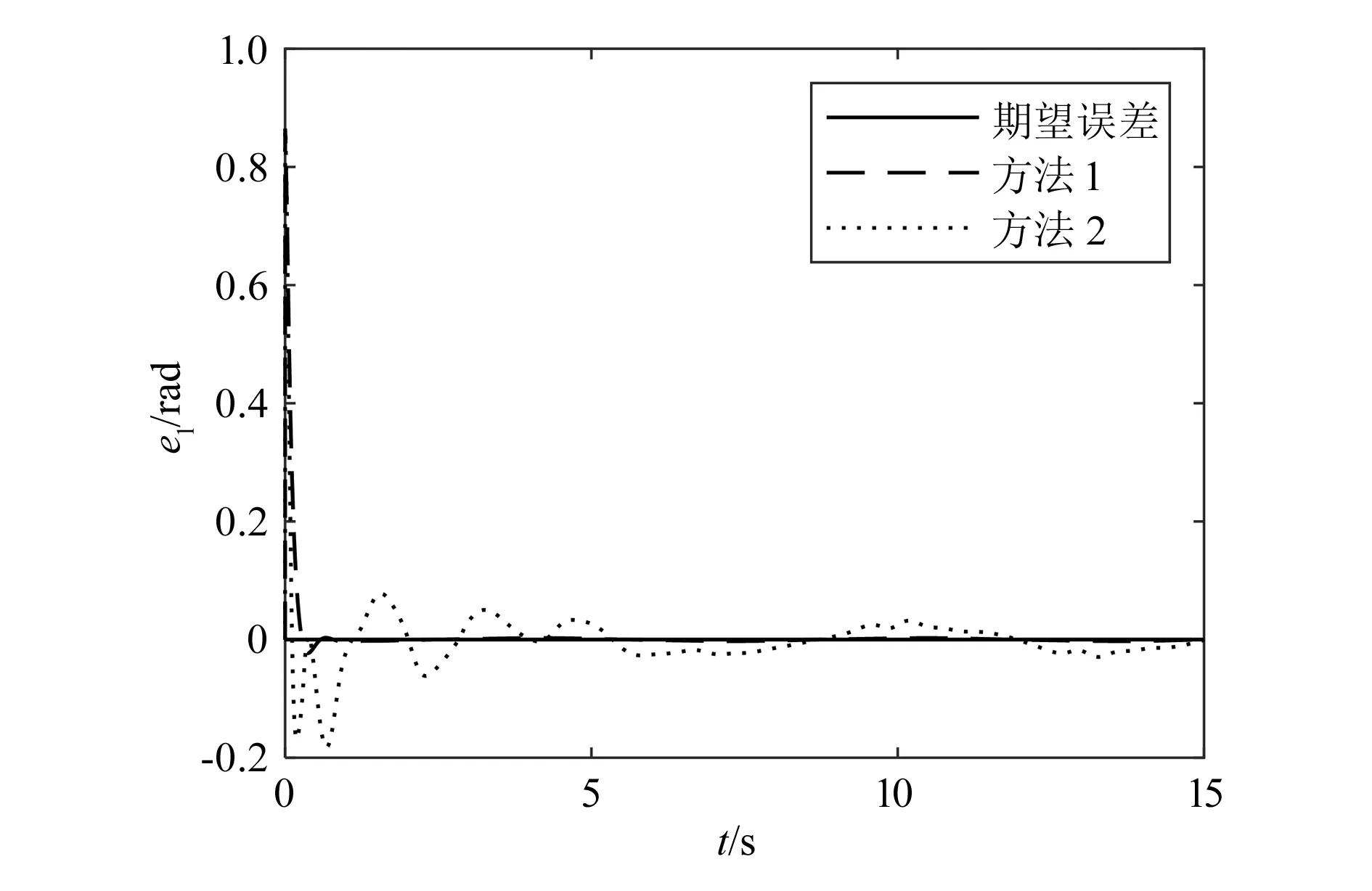
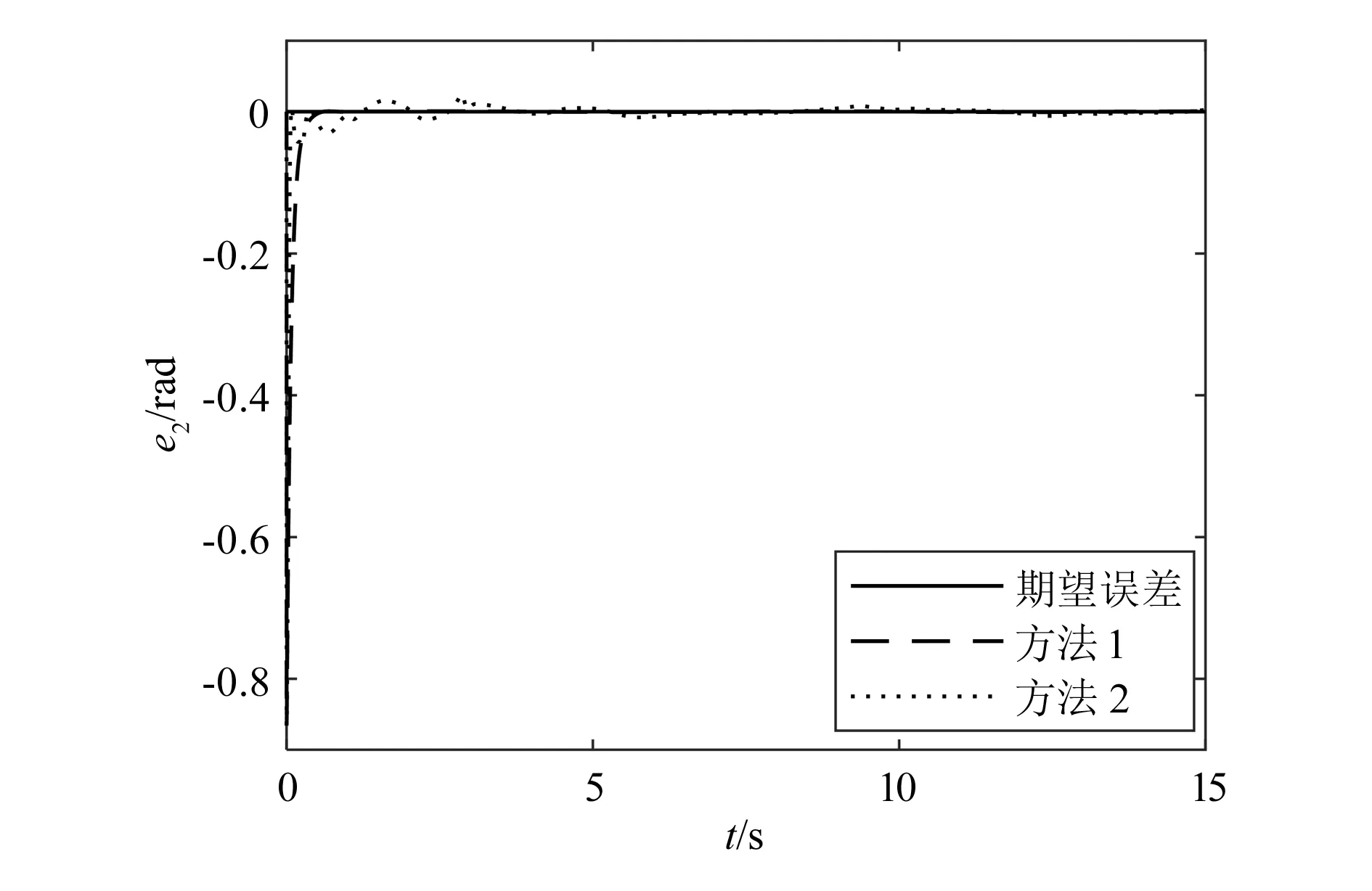
如果|s| (29) 则 (30) (31) 为了验证本文提出的控制器使得系统具有快速的学习能力和快速的收敛性,并且能够补偿结构和非结构的不确定性,与文献[16]提出的控制方法进行了仿真对比。假设外部对机械臂的干扰为τd=[0.2sint0.2sint0.2sint]T;载体、机械臂杆1与2的质量分别为m0=40 kg,m1=2 kg,m2=1 kg;转动惯量分别为J0=34.17 kg·m2,J1=1.5 kg·m2,J2=0.75 kg·m2;杆长分别为l0=1.5 m,l1=3 m,l2=3 m;其中OC1在x1轴上与O1的距离a1=1.5 m,OC2在x2轴上与O2的距离a2=1.5 m。网络初始权值为0,基函数宽度选为10,基函数中心在神经网络输入值的值域中选取,设刚性臂载体姿态角、机械臂各关节铰的期望运动规律分别为: θ0d=sint MATLAB仿真的载体姿态角、关节角1、关节角2初值分别设置为θ0=0°,θ1=0°,θ2=0°,各个参数初值分别设置为KP=216,Ks=diag(216,216,216),KDd=0.2,KCc=0.2,FD=FC=diag(0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2,0.2),γ=1.3,λ=(13,13,13)。利用本文给出的神经网络鲁棒自适应滑模控制方案对系统进行数值模拟仿真运算,整个仿真过程共耗时15.0 s,方法1为本文设计的控制方法,方法2为文献[16]中的控制方法。 图3、图4和图5分别为两种算法关于载体姿态角、关节角1和关节角2实际轨迹追踪期望轨迹对比图。图6、图7和图8分别为载体姿态角、关节角1和关节角2实际轨迹追踪期望轨迹的误差对比图。由图可以看出,对于载体姿态角,方法1控制系统在0.6 s左右完全跟踪期望轨迹,最大误差为6×10-3rad;在2.7 s左右,方法2控制系统完全跟踪期望轨迹,最大误差为9×10-2rad。对于关节角1,方法1控制系统在0.5 s左右完全跟踪期望轨迹,最大误差为3×10-3rad;方法2控制系统在1.1 s左右完全跟踪期望轨迹,最大误差为5×10-2rad。对于关节角2,方法1控制系统在0.6 s左右完全跟踪期望轨迹,最大误差为6×10-4rad;方法2控制系统在0.9 s完全跟踪期望轨迹,最大误差为1.5×10-2rad。综上所述,在3个角的实际轨迹拟合期望轨迹上,无论是完全拟合期望轨迹所需的时间还是在精度上,本文设计的控制器都要优于文献[16]的神经网络鲁棒控制器,所需时间更短,也更精确。 图3 载体姿态角轨迹跟踪 图4 关节角1轨迹跟踪 图5 关节角2轨迹跟踪 图6 载体姿态角误差 图9、图10和图11分别为控制载体姿态角、关节角1和关节角2所需力矩对比图,其中图9为方法1控制系统(含有符号函数)输入力矩图,图10为改进后方法1控制系统(用饱和函数替代符号函数后)输入力矩图,图11为文献[15]的神经网络鲁棒控制器输入力矩图。由图可以看出,方法1控制系统含符号函数时,输入力矩图存在很严重的抖振(图9),而用饱和函数sat(s)替换符号函数sgn(s)后,饱和函数可有效地抑制系统输入力矩的抖振,使实际的控制输入变得更平滑(图10)。稳定后,方法1控制系统控制载体姿态角、关节角1、关节角2所需最大输入力矩分别为57 N·m、26.5 N·m和5 N·m。图11显示,神经网络鲁棒控制器在稳定以后控制载体姿态角、关节角1、关节角2所需最大输入力矩分别为116 N·m、53 N·m和10 N·m。由图可见,方法1控制系统输入力矩达到稳定所需时间少,力矩既平滑,又相对小,耗用能源少。 图7 关节角1误差 图8 关节角2误差 图9 RBFNNs输入力矩 图10 改进后RBFNNs输入力矩 图11 RBF2输入力矩 针对空间机械臂在载体位置不受控、姿态受控的状态下,建立模型误差与外部干扰同时存在时的机械臂模型,提出了用RBF神经网络对系统进行基于模型分块逼近的自适应鲁棒控制,通过与文献[16]的控制方法进行对比可以看出,本文所提出的基于径向基函数神经网络的鲁棒自适应控制方案在实际轨迹追踪期望轨迹方面,无论是载体姿态角,关节角1还是关节角2,明显比文献[16]的控制方法更快,误差更小,具有控制性能稳定、输入力矩更小且更平滑的优点。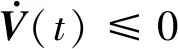
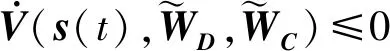

3 计算仿真与比较




4 结束语

