分数阶模糊微分方程周期边值问题解的存在唯一性
席艳丽,陈鹏玉
(西北师范大学 数学与统计学院,甘肃 兰州 730070)
0 引言
分数阶模糊微分方程是模糊数学的重要组成部分,分数阶模糊微分方程初边值问题是分数阶模糊微分方程定性理论的基本研究对象之一.与整数阶模糊微分方程相比,分数阶模糊微分方程具有分数阶导数的非局部性和记忆性的优点,例如在现实世界的各种物理问题的建模中有巨大的应用潜力,包括地震模型、流体力学模型和黏弹性材料性质的测量等等.因此,分数阶模糊微分方程初边值问题的解以及相关理论的研究引起了许多学者的广泛关注[1-3].
2014 年,Armand 等[1]运用Schaefer 不动点定理研究了模糊分数阶微分方程初值问题


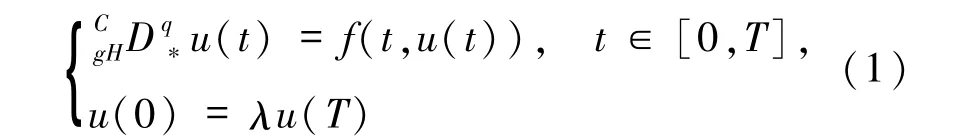
1 预备知识及引理
1965 年,Zadeh 给出了模糊集合的如下定义:所谓论域(非空集)X 上的一个模糊子集A,是指对任意x∈X,存在μA(x)∈[0,1]与x 对应,并且称μA(x)为x属于模糊子集A 的隶属程度,即模糊子集A指的是映射μA:X→[0,1]),也称μA为A的隶属函数,简记μA(x)为A(x).在不致引起误解的情况下,对模糊子集A 与它的隶属函数A(x)不加区别,同时模糊子集简称模糊集.
定义1.1[4]设E ={u|u:R→[0,1]且满足下面性质(i)~(iv)}.
(i)u 是正规的模糊集,即存在x0∈R,使得u(x0)=1;
(ii)u是凸的,即对任意的x1,x2∈R,λ∈(0,1),有u(λx1+(1 -λ)x2)≥min{u(x1),u(x2)};
(iii)u是上半连续函数;
(iv)u 的支集Supp 的闭包cl{x∈R|u(x)>0},记为[u]0,是紧的.则称u 是一个(1 维)模糊数,而所有(1 维)模糊数的全体称之为(1 维)模糊数空间,记为E.

定义1.2[6](Hukuhara差分)设w1,w2∈E,若存在w3∈E,使得w1=w2+w3,则w3被称为w1与w2的Hukuhara 差分.记作w1⊖w2.(注意:本文中,符号“⊖”表示差分,且w1⊖w2≠w1+(-1)w2.)
记CE([a,b])表示区间[a,b]上所有连续模糊函数的集合,LE([a,b])表示区间[a,b]上所有可测且可积的模糊数值函数的集合.
定义1.3[7]设模糊数值函数F ∈CE([a,b])∩LE([a,b]),则q ∈(0,1]阶Riemann-Liouville型分数阶积分有如下定义:

引理1.1[8]设F:[a,b]→E 是可积的模糊数值函数,且p,q >0,则).
定义1.4[9](Caputo gH-导数)设F ∈CE([a,b])∩LE([a,b]).若

等式右端积分逐点有定义,其中q∈(m -1,m],m∈N+,则称模糊数值函数F存在gH-可微意义下的q 阶Caputo 型分数阶导数,简称Caputo gH-导数.
定义1.5[9]设F:[a,b]→E 在t0∈(a,b)点Caputo gH-可微.如果F在t0点满足

那么称F在t0点C[(i)-gH]型可微;如果F在t0点满足
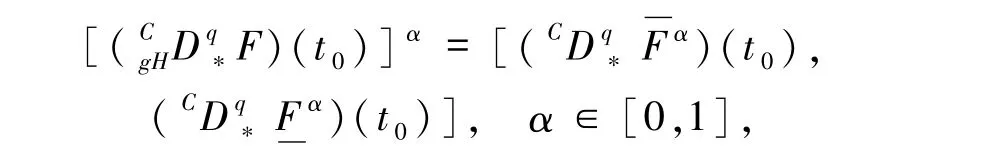
那么称F在t0点C[(ii)-gH]型可微.

引理1.3[11]任意给定u,v,w,x,y∈E,有如下性质成立:
(i)若u =v,当且仅当u≤v且u≥v;
(ii)若u≤v,则u+w≤v+w;
(iii)若u≤v且x≤y,则u+x≤v+y;
(iv)若u≤v且M∈R,则Mu≤Mv.
定义1.7[12]设函数ψ:[0,+∞)→[0,+∞)满足:(i)ψ 是连续非减函数;(ii)ψ(t)=0当且仅当t =0,则称ψ是一个距离选择函数.
定义1.8[13]设(X,d)是度量空间,函数f:X→X.如果存在距离选择函数ψ 和φ,使得对任意的x,y∈X,有

引理1.4[14]设(X,≤)是一个偏序集,且在X中存在一个度量d,使得(X,d)是一个完备的度量空间;函数f:X→X是非减函数,使得对于某些距离选择函数ψ和φ,满足

假设X满足对任意的n∈N,若非减序列(或者非增序列){xn}n∈N收敛到x∈X,则xn≤x;或者满足f连续.若存在x0∈X 使得x0≤f(x0)(或者x0≥f(x0)),则f有一个不动点.
引理1.5[14]在引理1.4 的假设条件下,若X中的每对元素有一个上界或者下界,则f 存在唯一的不动点.另外,若x0是f 的不动点,则对于任意x∈X,都有.
注1.1在空间(E,≤)和(CE[a,b],≤)上,任意元素对总有上界.
2 主要结果
定义2.1设模糊数值函数u∈CE[0,T]是满足边值问题(1)的解.如果边值问题(1)的解是C[(i)-gH]型可微的,那么称其为(i)型解;如果边值问题(1)的解是C[(ii)-gH]型可微的,那么称其为(ii)型解.
定义2.2设模糊数值函数u ∈CE[0,T],如果

那么称u是模糊边值问题(1)的一个下解.特别地,如果u 是C[(i)-gH]型可微的(或者C[(ii)-gH]型可微的),那么称u 为(i)型下解(或者(ii)型下解);如果

那么称u是模糊边值问题(1)的一个上解.特别地,如果u是C[(i)-gH]型可微的(或者C[(ii)-gH]型可微的),那么称u 为(i)型上解(或者(ii)型上解).
在CE[0,T]中,设存在ρ >0,λ∈[0,1)∪(1,+∞),使得当ρ 充分大时,成立,度量

对任意的u,v∈CE[0,T],度量Dρ等价于度量D,且(CE[0,T],Dρ)是一个完备的度量空间[15].
定理2.1假设边值问题(1)存在一个(i)型下解u∈CE[0,T],如果函数f:[0,T]×E→E 连续且满足:
(H1)f关于第二变量是非减的,即对于所有的t∈[0,T],若u≥v,则f(t,u)≥f(t,v);
(H2)f对于可比较元素来说是弱压缩的,即对任意的u≥v,存在2 个距离选择函数φ 和ψ,使得ψ(d(f(t,u),f(t,v)))≤ψ(d(u,v))-φ(d(u,v)),那么边值问题(1)在[0,T]上存在唯一的(i)型解.
证明设λ∈(0,1),q∈(0,1]时,如果y 是C[(i)-gH]型可微的,则边值问题(1)等价于积分方程

故定义算子A:CE[0,T]→CE[0,T]如下:
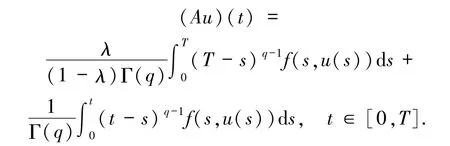
其中,λ∈(0,1),u 是边值问题(1)的(i)型解当且仅当u =Au.证明分为以下4 步.
步骤1 算子A是非减的.由文献[12]中模糊值函数的积分性质及条件(H1)知,对于u≥v,t∈[0,T],λ∈(0,1),有

因此算子A是非减的.
步骤2 算子A是弱压缩的.由条件(H2),若u≥v,则有ψ(d(f(t,u),f(t,v)))≤ψ(d(u,v)),t∈[0,T].由距离选择函数ψ 的单调性及条件(H2),对任意u≥v,有d(f(t,u),f(t,v))≤d(u,v),t∈[0,T].由Dρ和A的定义,有
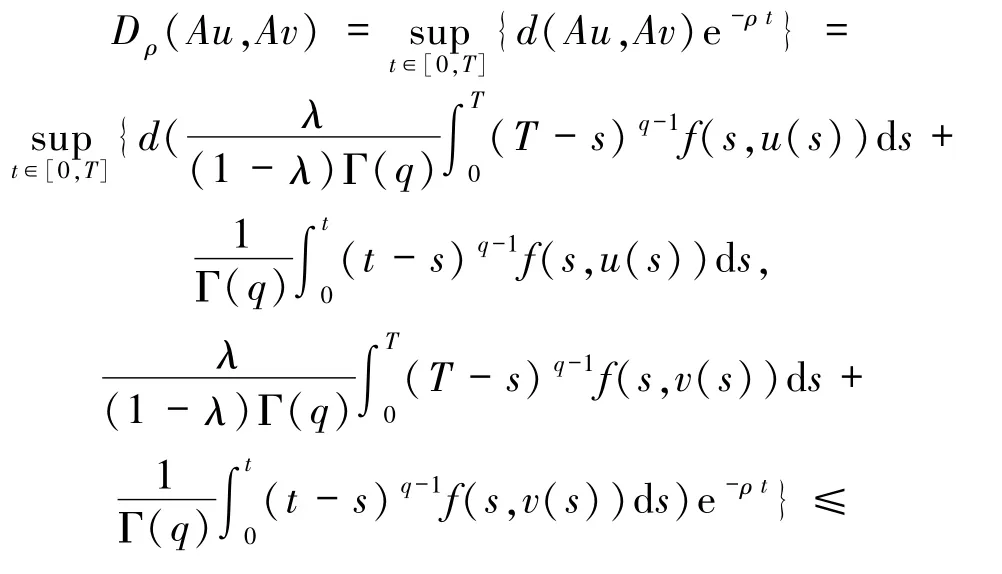

当u≥v时,对于距离选择函数ψ,

因此,算子A是弱压缩的.
步骤3 算子A 是连续的.设u,v∈CE[0,T]且u≥v,与步骤2 类似,有

因此,对任意的ε >0,当

时,D(Au,Av)≤ε,即A是连续算子.
步骤4 由(i)型下解的存在性及引理2.1 有
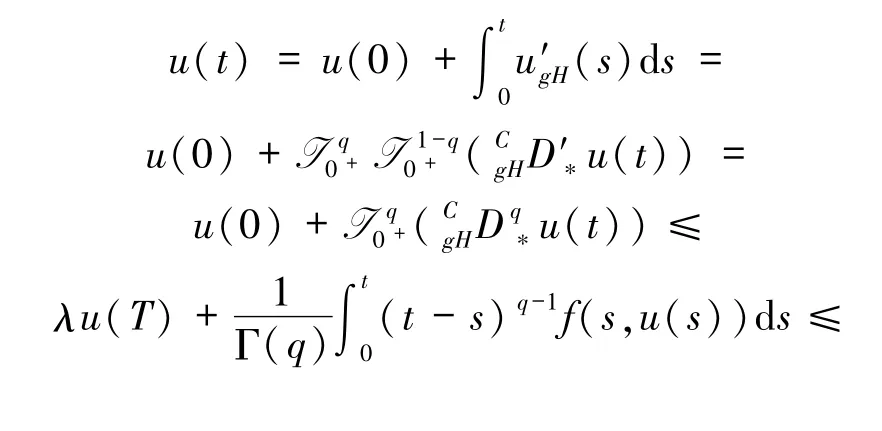

因此,u≤Au,由引理1.4 知,算子A在CE[0,T]中有一个不动点.假设CE[0,T]中的每一对元素都有上界,则由引理1.5 知,算子A存在唯一的不动点.因此,边值问题(1)在[0,T]上存在唯一的(i)型解.
定理2.2假设边值问题(1)存在一个(i)型上解v∈CE[0,T],如果函数f:[0,T]×E→E 连续且满足条件(H1)和(H2),则边值问题(1)在[0,T]上存在唯一的(i)型解.
证明若v是边值问题(1)的一个(i)型上解,则对任意的t∈[0,T],λ∈(0,1)有
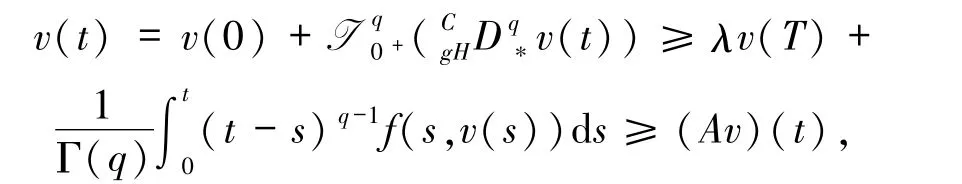
因此,v≥Av.进一步假设CE[0,T]中每一对元素都有一个上界,再由引理1.4,算子A 存在唯一的不动点.
定理2.3假设边值问题(1)存在一个(ii)型下解u∈CE[0,T],如果函数f:[0,T]×E→E 连续,且满足条件(H1)~(H3).
(H3)对所有α∈[0,1],λ∈(1,+∞),有
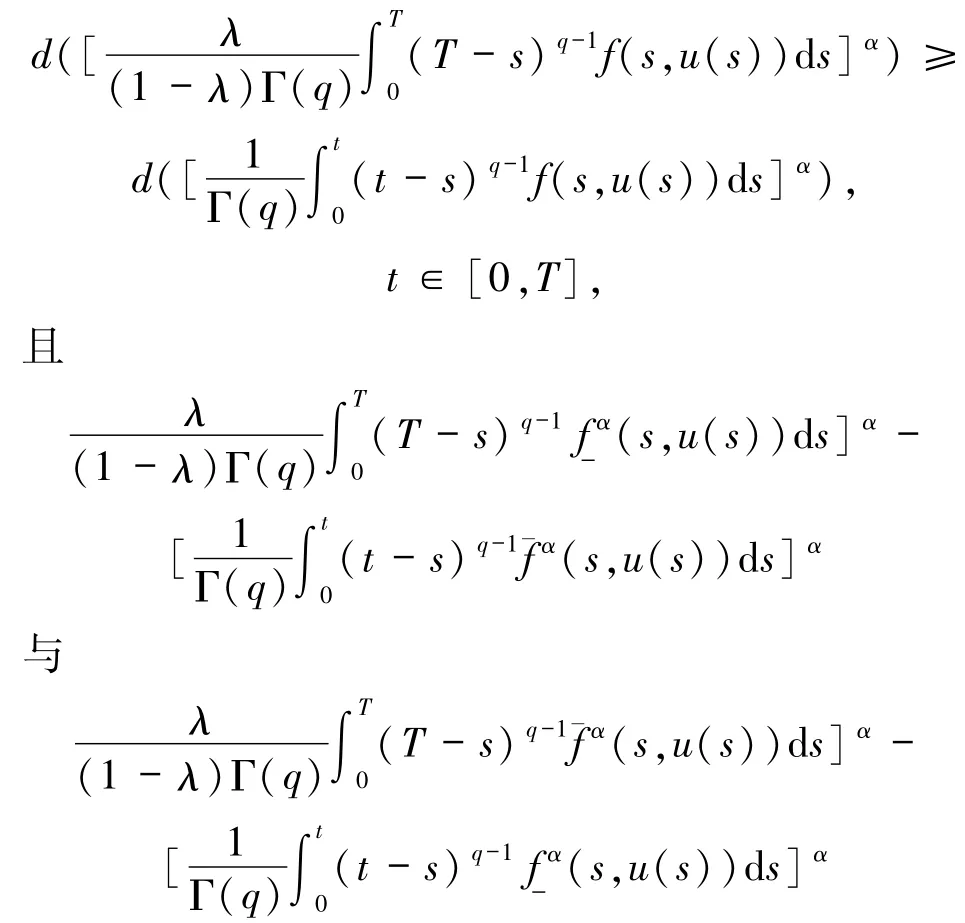
关于α分别单调递增和单调递减,那么边值问题(1)在[0,T]上存在唯一的(ii)型解.
证明设λ∈(1,+∞),q∈(0,1]时,如果y是C[(ii)-gH]型可微的,边值问题(1)等价于积分方程

故定义算子B:CE[0,T]→CE[0,T]如下:

其中λ∈(1,+∞),若u 是边值问题(1)的(ii)型解当且仅当u =Bu.由条件(H3)和文献[8]中的表示定理知,上述等式右端积分在[0,T]上有定义,证明分为以下4 步.
步骤1 算子B是非减的.由文献[12]中的模糊值积分性质及条件(H1)知,对于u≥v,t∈[0,T],λ∈(1,+∞),有

因此算子B是非减的.
步骤2 算子B是弱压缩的.由定理3.1 证明中的步骤2,有

当u≥v时,对于距离选择函数ψ,有
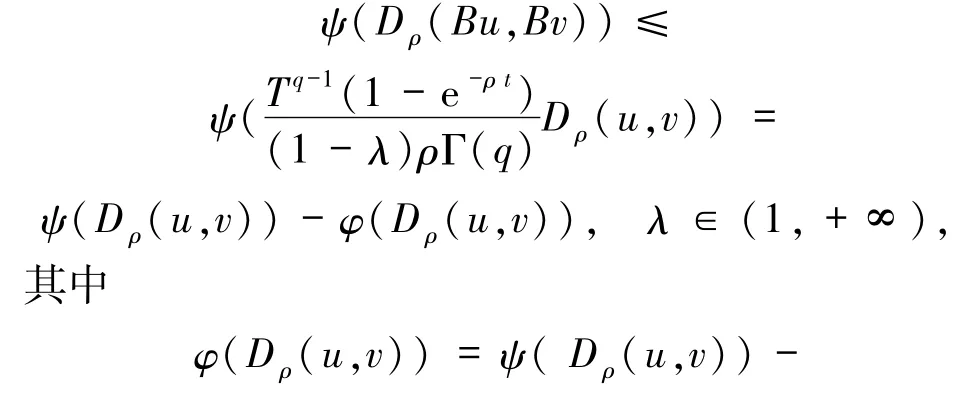

因此,算子B是弱压缩的.
步骤3 算子B 是连续的.设u,v∈CE[0,T]且u≥v,λ∈(1,+∞),有

因此,对任意的ε >0,当

时,D(Bu,Bv)≤ε,即B是连续算子.
步骤4 由(ii)型下解的存在性及引理1.1 有

因此,u≤Bu,由引理1.4 知,算子B在CE[0,T]中有一个不动点.假设CE[0,T]中的每一对元素都有上界,则由引理1.5 知,算子B存在唯一的不动点.因此,边值问题(1)在[0,T]上存在唯一的(ii)型解.
定理2.4假设边值问题(1)存在一个(ii)型上解v∈CE[0,T],如果函数f:[0,T]×E→E 连续且满足条件(H1)~(H3),那么边值问题(1)在[0,T]上存在唯一的(ii)型解.
证明若v 是边值问题(1)的一个(ii)型上解,则对任意的t∈[0,T],λ∈(1,+∞),有

因此,v≥Bv.进一步假设CE[0,T]中每一对元素都有一个上界,再由引理1.4,算子B 存在唯一的不动点.
致谢西北师范大学青年教师科研能力提升计划资助项目(NWNU-LKQN2019-3)和西北师范大学参与式研讨课教学改革项目对本文给予了资助,谨致谢意!

