多种解题视角下的别样精彩
——品味2021年浙江高考填空压轴题
浙江 尹 健 沈 恒
平面向量是中学数学的重点和难点,也是浙江高考填空题中的“最高峰”.对于如此重要的一道题,笔者在这里先提出三个问题:第一,如何有效地解答高考真题中的平面向量试题?第二,命题专家在出题时怎么考查平面向量的知识点与其他内容的综合性?第三,根据试题的导向,我们的教学该怎么调整?笔者以为,每一年高考试题都会带给一线教师值得回味之处.在刚刚结束的2021高考中,浙江卷平面向量朴实无华,在容易上手的同时又能凸显学生的能力,强调基础又重视能力,较好的区分了学生的水平和层次,值得一线教学深思.
1.问题
(2021·浙江卷·17)已知平面向量a,b,c(c≠0),满足|a|=1,|b|=2,a·b=0,(a-b)·c=0,记平面向量d在a,b方向上的投影分别为x,y,d-a在c方向上的投影为z,则x2+y2+z2的最小值为.
分析:本题涉及四个向量,三个参数,第一眼看上去非常复杂,但根据平面向量基本定理,四个向量都可以用a,b作为基底表示,而由a,b的垂直关系可以借助坐标系来进行运算,三个参数之间也有一些联系,从而达到消参的目的,但是始终会剩下两个无关变量x,y,接下来该怎么处理呢?对于含有两个变量的最值问题,一种方法可以先固定一个变量x或y,将其看成常数,借助函数的方法来解决;另一种方法是借助不等式来统一解决;由于向量本身具有几何意义,所以本题也可以从几何图形的视角入手,这里从条件提供的向量关系来作出图象,即投影的概念,那么所涉及的参数也可以赋予几何意义,从而简化问题,直至解决.可以这么说,今年浙江卷平面几何试题的命制入口较宽,方法较多,计算较简洁,具有浓烈的浙江特色.下面我们先来看看多种常用解法.
2.解法
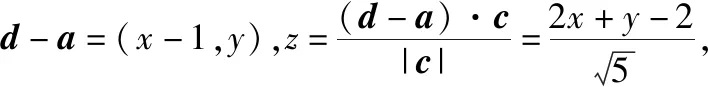

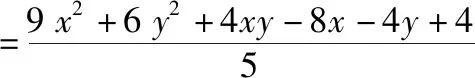


说明:坐标法是平面向量中常用的方法,也是学生在考试中最优先选择的方式,因此学生突破本题时,最容易想到的正是此方法.而且由于题目给出|a|=1,|b|=2,a·b=0,所以非常容易建立坐标系,之后的c,d等向量都可以用坐标表示出来,根据投影的概念,z也可以用x,y表示出来,到这一步为止,对于大部分学生来说都可以完成.但是接下来,x2+y2+z2即使代入消去z,表达式中仍有x,y两个变量,这两个变量没有任何相互关系,所以无法利用代入消元法.通过进一步分析发现,我们可以选用逐个击破的方式,先将y看成常数,表达式看成关于x的二次函数,由二次函数的最小值消去x,这样一来,表达式就变成关于y的二次函数,最后就可以直接求出此二次函数的最小值.此方法消去的参数是x,那么能不能消去y呢?当然是可以的,具体解法如下.
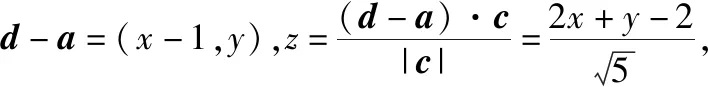

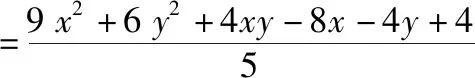
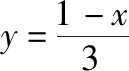

说明:本解法与解法一类似,只是消去的参数不同,所以重复的地方不再赘述.上述两种方法,都是学生在考试时容易想到的方法,操作起来也具有时效性.但是.由于上述两种方法都不可避免地要消去x,y其中的一个,所以步骤较多,计算量较大,消耗的时间较多.那么如何不用消参,可以更加高效地解决问题呢?我们可以借助不等式.
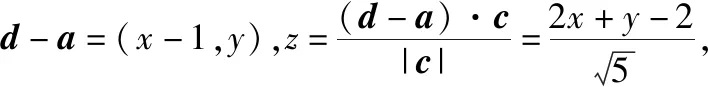
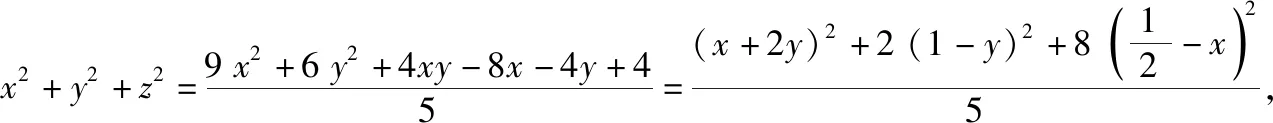
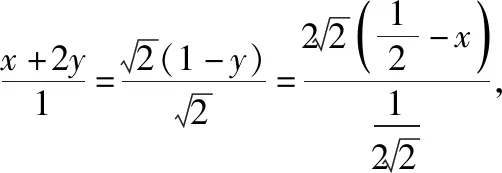
说明:有关两变量的最值问题,不等式是一种比较快捷、实用的方法.而此方法使用的是柯西不等式,通过比较可以发现,此方法比前两种方法的计算要少,在得到表达式后只需一步即可求出最终答案,笔者在写的时候将这最后一步拆成多个步骤的目的主要是为了阅读时更加清晰,在实际考试时,只要列一个柯西不等式即可得出答案.然而,柯西不等式这个内容本身对学生的水平要求较高,而且在等式变形的时候配方也是一个不小的难点,所以虽然计算简化了,但思维的要求却提高了.而且此方法只是简化了后半程的计算,前半程还是和前两种方法一致,这就是坐标法的弊端,一定会有比较复杂的计算过程.为了克服这种弊端,我们需要抛弃坐标,利用平面向量的几何性质.
解法四(几何法1):





说明:可以看到,当我们将向量的几何性质与代数性质结合得到图象之后,题目涉及的参数也被赋予了几何意义,从一开始减少了变量,后续的运算也简单了,有效地提高了解题效率.虽然将变量改为|d|与θ比前三种方法要简洁,但是我们发现最后还是绕不开双变量问题,这并没有解决本题最核心的难点,所以接下来我们继续将此方法优化,寻找单一变量.
解法五(几何法2):
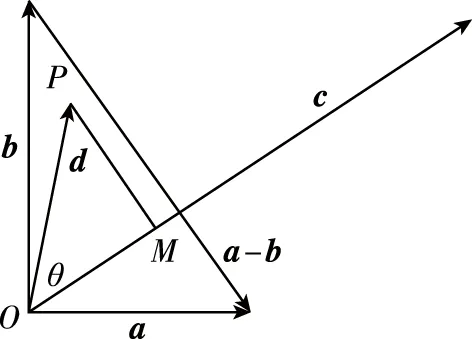

说明:比较解法四与解法五,我们发现如果进一步去理解图形,那么从一开始我们就可以将参数减少到最少,直接变成一个单一变量的二次函数最值问题,这样一来,我们只需要花费前几种方法一半的时间,就可以解决此题.因此我们深深地认识到,平面向量具有代数和几何的双重身份,将两者结合起来解决问题,往往是解题的最佳方案.
3.对比
命题组对试题的命制考虑周全,解决问题的切入口是开阔的.这就凸显了高考真题以通性通法为基本依据的特性,透过本题思考高三的平面向量复习教学应该怎么做呢?让我们从上述常规的解法中来判断、辨别和思考(如下表):
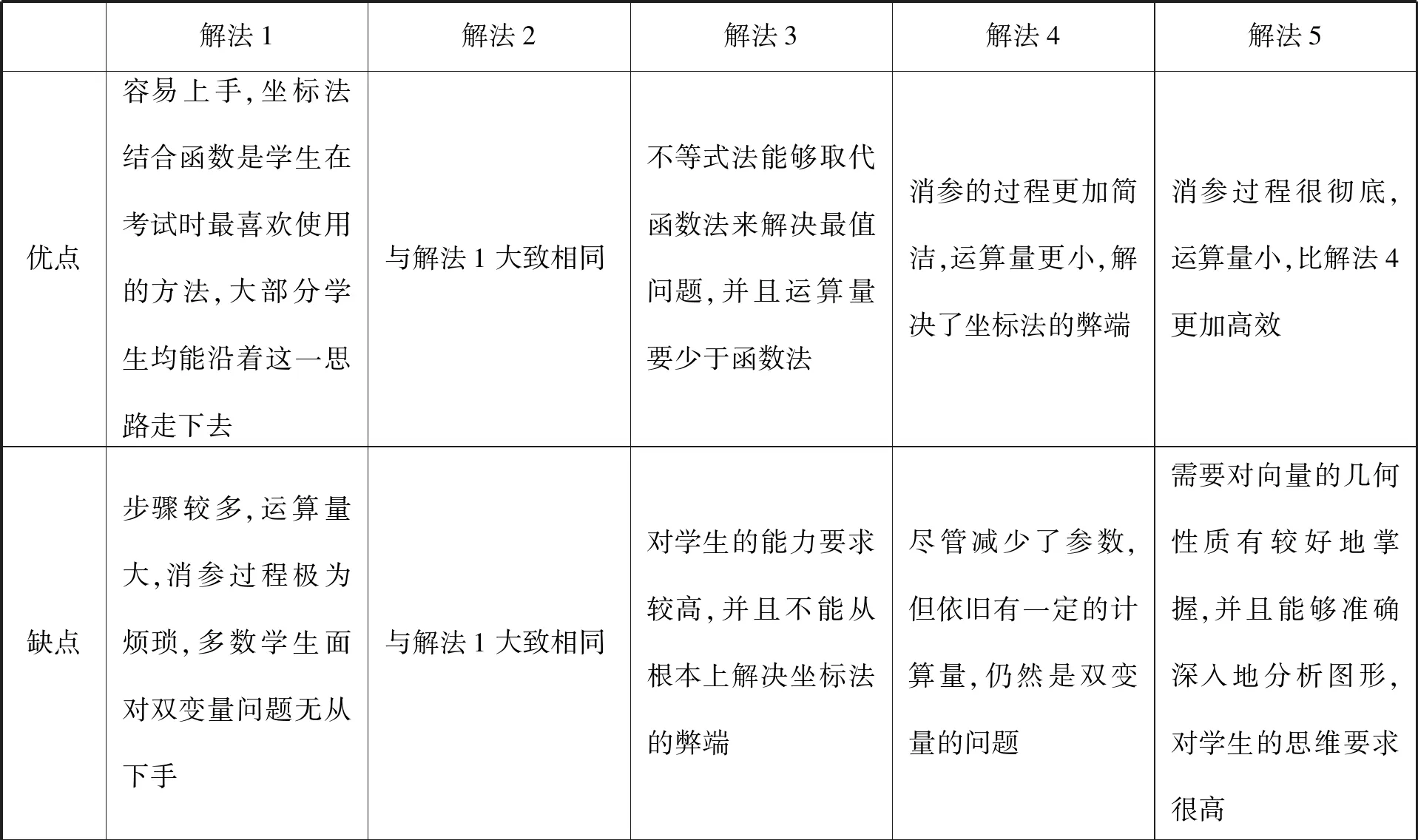
解法1解法2解法3解法4解法5优点容易上手,坐标法结合函数是学生在考试时最喜欢使用的方法,大部分学生均能沿着这一思路走下去与解法1大致相同不等式法能够取代函数法来解决最值问题,并且运算量要少于函数法消参的过程更加简洁,运算量更小,解决了坐标法的弊端消参过程很彻底,运算量小,比解法4更加高效缺点步骤较多,运算量大,消参过程极为烦琐,多数学生面对双变量问题无从下手与解法1大致相同对学生的能力要求较高,并且不能从根本上解决坐标法的弊端尽管减少了参数,但依旧有一定的计算量,仍然是双变量的问题需要对向量的几何性质有较好地掌握,并且能够准确深入地分析图形,对学生的思维要求很高

续表
4.建议
学生非常熟悉平面向量的基础知识,但是大部分学生在面临平面向量难题的时候往往不能通晓其究竟,笔者将其归结为三种症结:
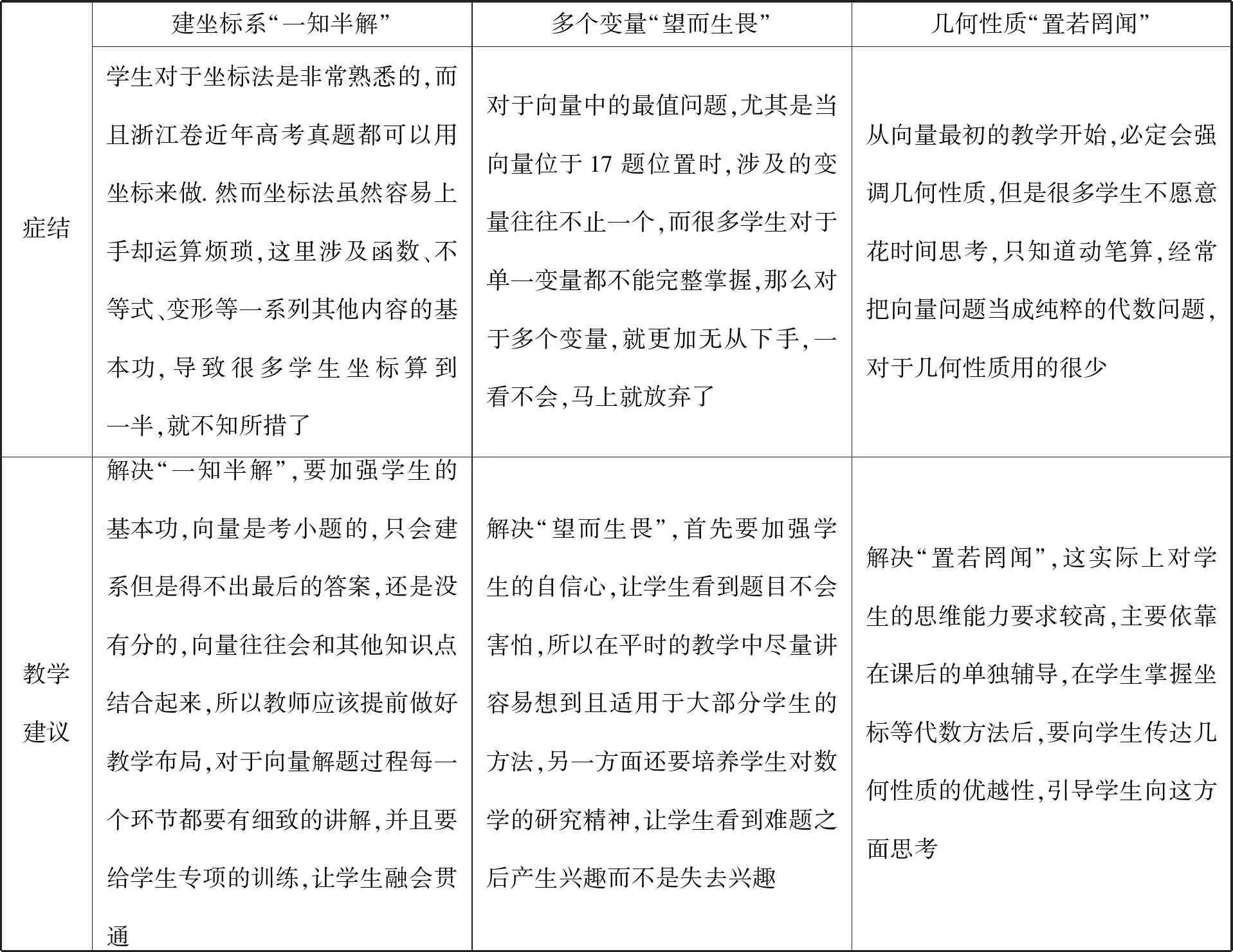
症结建坐标系“一知半解”多个变量“望而生畏”几何性质“置若罔闻”学生对于坐标法是非常熟悉的,而且浙江卷近年高考真题都可以用坐标来做.然而坐标法虽然容易上手却运算烦琐,这里涉及函数、不等式、变形等一系列其他内容的基本功,导致很多学生坐标算到一半,就不知所措了对于向量中的最值问题,尤其是当向量位于17题位置时,涉及的变量往往不止一个,而很多学生对于单一变量都不能完整掌握,那么对于多个变量,就更加无从下手,一看不会,马上就放弃了从向量最初的教学开始,必定会强调几何性质,但是很多学生不愿意花时间思考,只知道动笔算,经常把向量问题当成纯粹的代数问题,对于几何性质用的很少教学建议解决“一知半解”,要加强学生的基本功,向量是考小题的,只会建系但是得不出最后的答案,还是没有分的,向量往往会和其他知识点结合起来,所以教师应该提前做好教学布局,对于向量解题过程每一个环节都要有细致的讲解,并且要给学生专项的训练,让学生融会贯通解决“望而生畏”,首先要加强学生的自信心,让学生看到题目不会害怕,所以在平时的教学中尽量讲容易想到且适用于大部分学生的方法,另一方面还要培养学生对数学的研究精神,让学生看到难题之后产生兴趣而不是失去兴趣解决“置若罔闻”,这实际上对学生的思维能力要求较高,主要依靠在课后的单独辅导,在学生掌握坐标等代数方法后,要向学生传达几何性质的优越性,引导学生向这方面思考


