立体几何中与球有关的问题

江苏 夏雪峰

与球有关的问题是学生在学习立体几何时经常碰到的内容，一方面从教材(人教2019A必修第二册)中来看，涉及球的例习题并不多(P118例3、P119例4、P119练习3、P120习题5、P169复习参考题3，共5个)，具体内容主要是常见的组合体、内切球与外接球相关的面积、体积等问题.另一方面从高考题中来看，涉及球的内容倒不少，下表是2016至2021年各卷区高考真题中涉及球的简单统计：

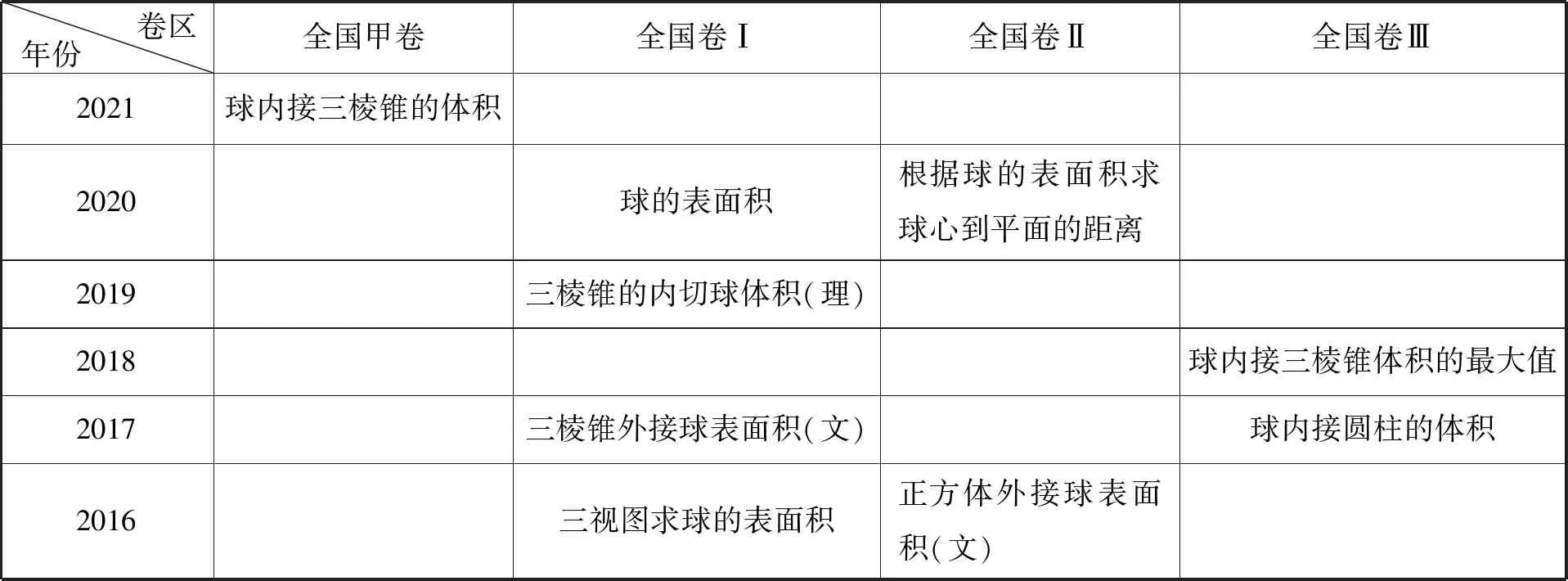
卷区年份全国甲卷全国卷Ⅰ全国卷Ⅱ全国卷Ⅲ2021球内接三棱锥的体积2020球的表面积根据球的表面积求球心到平面的距离2019三棱锥的内切球体积(理)2018 球内接三棱锥体积的最大值2017 三棱锥外接球表面积(文)球内接圆柱的体积2016 三视图求球的表面积正方体外接球表面积(文)

从表中以及高考真题可以看出，全国卷对于球的考查有以下几个特征：

1.考查的题型：选择或填空，难度以中档题为主；

2.考查的模型：球内接三棱锥、球内接三棱柱、球内接圆柱、球内接长方体(正方体)、组合体等；

3.考查的问题：球外(内)接几何体体积、表面积与体积的运算等.

从平时的教学中发现，不少学生对球的相关问题存在解题思路不明、解题方法及计算不到位等问题，这一方面与学生的数学基础尤其是空间想象能力有关，其次也提醒教师要有针对性地教学.我们知道立体几何主要培养学生的空间想象能力，球是非常好的载体，这也是高考频繁考查球相关问题的一个因素.所以非常有必要对球的问题有一个系统的认识与掌握，下面分几类常见问题说明.

一、组合体问题

【例1】(人教版2019A版必修第二册P118例3)如图，某种浮标由两个半球和一个圆柱黏合而成，半球的直径是0.3 m，圆柱高0.6 m.如果在浮标表面涂一层防水漆，每平方米需要0.5 kg涂料，那么给1 000个这样的浮标涂防水漆需要多少涂料？(π取3.14)

【解析】一个浮标的表面积为2π×0.15×0.6+4π×0.152=0.847 8(m2)，所以给1 000个这样的浮标涂防水漆约需涂料0.847 8×0.5×1 000=423.9(kg).

【教学建议】这是一个组合体，教学中只需引导学生能确定此组合体由圆柱与两个半球组合而成，计算可以由学生自主完成.

【例2】如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm，如果不计容器的厚度，则球的体积为

( )

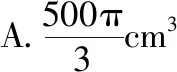
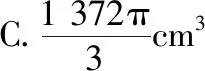
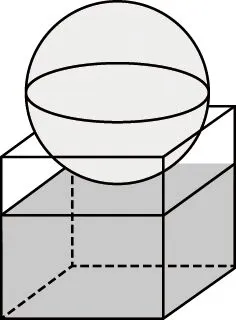
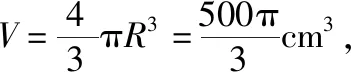
【教学建议】此题的关键有两点，一是找到球与正方体的组合方式——球与正方体四条棱相切；二是确定解题方法——取两个切点的球的一个大圆截面(如图)，转化为圆内的问题来处理.

二、球的截面问题

【例3】球O的两个相互垂直的截面圆O1与O2的公共弦AB的长为2，若△O1AB是直角三角形，△O2AB是等边三角形，则球O的表面积为

( )

A．9π B．12π C．16π D．20π

【解析】如图，连接OO1，OO2，则OO1⊥圆O1所在平面，

OO2⊥圆O2所在平面，取AB的中点E，连接O1E，O2E，则四边形OO1EO2为矩形．

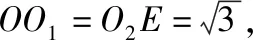
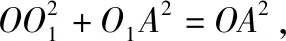
则球O表面积为4πR2=4π×5=20π，故选D．

【教学建议】首先，类比平面几何中的圆与弦的勾股关系，球的截面问题经常利用的核心关系是r2+O1O2=R2，此题也不例外.其次此题中有两个相互垂直的截面圆，可以引导学生通过建立方程组来求解.

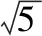
【解析】如图,取B1C1的中点为E，BB1的中点为F，CC1的中点为G，

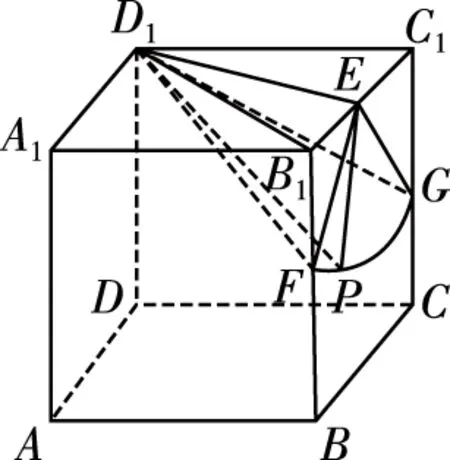
又四棱柱ABCD-A1B1C1D1为直四棱柱，所以BB1⊥平面A1B1C1D1，所以BB1⊥D1E，

因为BB1∩B1C1=B1，所以D1E⊥侧面B1C1CB，设P为侧面B1C1CB与球面的交线上的点，则D1E⊥EP.

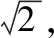
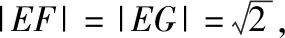
【教学建议】此题对空间想象能力要求较高，但只要抓住球的截面始终是圆及如何确定截面圆的圆心，便明确了方向.建议抓住三个要点：①平面BCC1B1球截面得到必然是圆；②确定截面圆的圆心是E；③确定该圆在侧面BCC1B1上的部分圆弧位置，计算长度.

三、外接球问题

1.三棱锥的外接球

【例5】(2019·全国卷Ⅰ理·12)已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为

( )

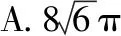
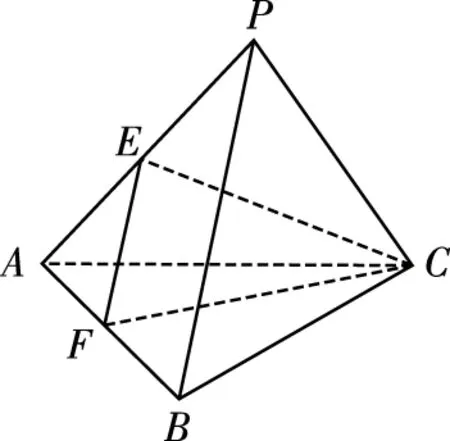
【解析】因为PA=PB=PC,△ABC为边长为2的等边三角形，

可知三棱锥P-ABC为正三棱锥，PB⊥AC，

又E，F分别为PA,PB的中点，

EF∥PB，所以EF⊥AC，

又EF⊥CE，CE∩AC=C,

EF⊥平面PAC，PB⊥平面PAC，

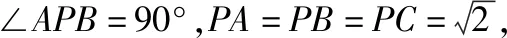
由三棱锥P-ABC为正方体一部分，

【教学建议】在多面体的外接球中，长方体、正方体的外接球较为常见.此题虽然条件中是三棱锥的外接球，但是通过引导学生进一步判断PA，PB，PC两两垂直，所以三棱锥是正方体的一部分，外接球的球心就不难确定了.在这个问题中，通过“判断”“补形”，将棱锥的外接球转化为正方体的外接球，非常巧妙，对培养学生的空间想象能力很有帮助.

( )

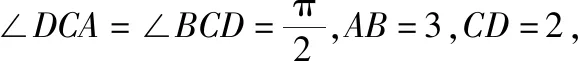
【解析】如图，设G为正三角形ABC的外心，

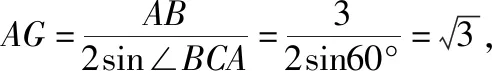
取BD的中点N，则N为直角三角形BCD的外心，

设三棱锥的外接球的球心为O，则ON⊥平面BCD，OG⊥平面ABC，

【教学建议】对学生而言，如何确定三棱锥的外接球的球心是难点，在教学过程中建议把作图过程特别是如何把球心找出来(或者构造出来)的过程一步一步详细展示出来，这样有助于分解难点.过底面(把合适的面作为底面)三角形的外心作底面的垂线，则外接球的球心必在此垂线上，然后由方程确定球的半径.

2.四棱锥的外接球

( )

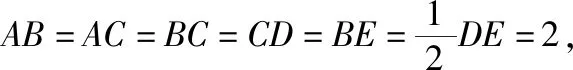
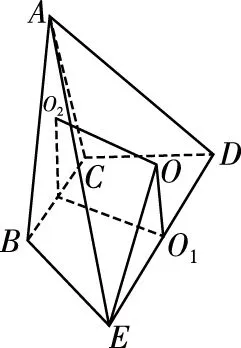
取DE的中点O1，

则O1D=O1E=O1B=O1C=2，

即O1为梯形BCDE的外接圆的圆心，

设四棱锥A-BCDE的外接球的球心为O，等边三角形ABC的外接圆的圆心为O2，

由侧面ABC⊥底面BCDE，

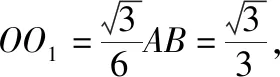
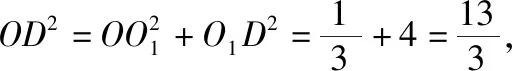
【教学建议】对于四棱锥的外接球，要让学生理解确定球心的方法与三棱锥类似，此题可以判断底面四边形是等腰梯形，它的外心可以确定，然后构造球心即可.

四、内切球问题

【例8】(1)(人教版2019A版必修第二册P119练习3)将一个棱长为6 cm的正方体铁块磨制成一个球体零件，求可能制作的最大零件的体积.

(2)(人教版2019A版必修第二册P119例4)如图，圆柱的底面直径和高都等于球的直径，求球与圆柱的体积之比.

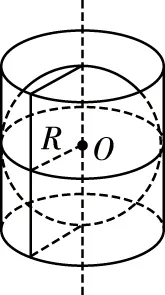
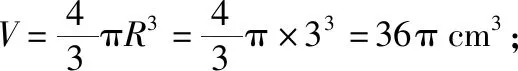
(2)设球的半径为R,则圆柱的底面半径为R，高为2R.

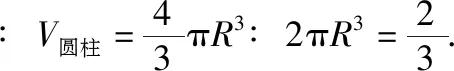
【教学建议】这是教材中两个非常好的例习题，教学中要充分发挥它们的价值.

对于(1)，重点让学生能理解所求最大体积就是求正方体的内切球的体积，

对于(2)，可以向学生说明著名的阿基米德圆柱体，并介绍相关的数学史料.

( )

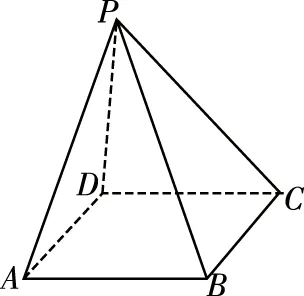
【解析】由题意，最大的球应与四棱锥各个面都相切，

设球心为S，连接SD，SA,SB,SC,SP，

则把此四棱锥分为五个棱锥，设它们的高均为R，求出四棱锥的表面积

【教学建议】教学中，可以通过类比思考的方式，引导学生类比平面几何中多边形的内切圆问题，得到棱锥的内接球,通过“等体积法”来确定球半径的常用方法，这样类比的方法可以让学生由浅入深地理解问题，掌握方法.

五、外切球问题

【例10】桌面上有3个半径为2 021的球两两相外切，在其下方空隙中放入一个球，该球与桌面和三个球均相切，则该球的半径为

( )

【解析】设三个半径为R的球的球心分别为O1，O2，O3，与桌面三个切点分别为A，B，C，如图所示，

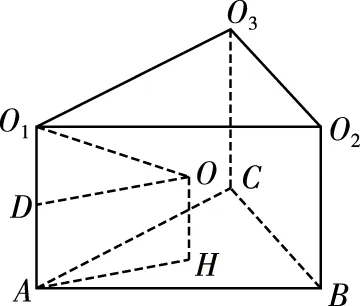
则三棱柱ABC-O1O2O3，是一个底面边长为2R，高为R的正三棱柱，

则小球球心O在底面ABC上的投影为△ABC的中心H，

连接OH，AH，OO1，作OD∥AH交O1A于点D，可得四边形AHOD为矩形，OD=AH.

设小球半径为r，则OH=AD=r，O1D=O1A-DA=R-r，

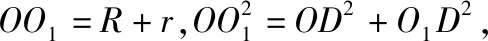
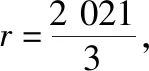
【教学建议】此题对学生的空间想象能力要求也很高，教学中一方面要引导学生抓住要点，即通过球心来构造三棱柱，另一方面通过类比圆的外切的方法，利用半径之和等于球心距进行计算.